2. 安徽理工大学空间信息与测绘工程学院,安徽省淮南市泰丰大街168号,232001
由于硬件延迟导致的接收机端和卫星端在2个不同频率或同一频率上不同码信号之间产生的差值称为差分码偏差(DCB),是电离层建模和精密单点定位中不可忽略的误差项。BDS-3在BDS-2的基础上新增B1C、B2a、B2b和B2等新频点,多种DCB有待估计:Wang[1]将IGGDCB方法应用于DCB估计,结果满足BDS全球系统建设的应用需求;张宝成等[2]提出利用非组合精密单点定位技术来估计卫星和测站的DCB,得到与CODE差值为0.1 ns的产品。还有学者通过研究MGEX产品对卫星单点定位的影响发现[3-5],DCB产品较大程度上提高了导航定位的性能。邓远帆等[6]首次全面分析了BDS-3的22种DCB产品后发现,直接估计的DCB精度高于线性估计的精度。
影响北斗高精度导航定位服务的关键参数主要受卫星数据质量的影响,其中伪距观测值的多路径延迟对高精度快速服务产品的影响较为明显[7]。基于此,本文针对BDS-3多路径延迟进行分析,首先在原始观测方程中得到BDS-3多路径延迟观测原始序列;然后利用机器学习中的正则化方法进行去噪处理[8],去噪后的序列按照趋势项和随机项分别用多项式模型和AR模型进行进一步处理[9];最后将处理后的结果作为伪距观测量中的多路径延迟改正项。
1 差分码偏差估计方法目前能稳定提供DCB产品的机构有欧洲定轨中心、中国科学院和德国宇航局等。DCB估计方法主要有2种:1)使用已有的高精度GIM产品消除电离层参数;2)同时估计DCB和电离层参数,得到卫星和测站的DCB组合值,通过零均值约束方程分离出接收机和卫星的DCB。本文使用第2种方法,首先估计BDS-3的11类DCB,然后按照稳定性、闭合差和CAS偏差进行分析,最后与CAS提供的DCB产品进行PPP精度比较。
1.1 DCB估计方法通常利用双频信号卫星观测数据提取DCB参数,伪距和相位观测方程为:
| $ \begin{aligned} P_{\mathrm{r}, k}^{\mathrm{s}}= & \rho_{\mathrm{r}}^{\mathrm{s}}+c\left(d_t^{\mathrm{r}}-d_t^{\mathrm{s}}\right)+\delta_{\text {ion }, k}+\delta_{\text {tro }}+ \\ & \delta_{\text {muit }, k}+d_{\mathrm{r}, k}+d_k^{\mathrm{s}}+\varepsilon_{P, k} \end{aligned} $ | (1) |
| $\begin{gathered} L_{\mathrm{r}, k}^{\mathrm{s}}=\rho_{\mathrm{r}}^{\mathrm{s}}+c\left(d_t^{\mathrm{r}}-d_t^{\mathrm{s}}\right)-\delta_{\mathrm{ion}, k}+\delta_{\text {tro }}+ \\ \delta_{\text {muit }, k}-b_{\mathrm{r}, k}-b_k^{\mathrm{s}}+\lambda_k N_K+\zeta_{L, k} \end{gathered} $ | (2) |
式中,r为接收机,s为卫星,k=i、j为2个不同的频率,Pr, ks和Lr, ks分别为接收机r和观测卫星s在k频率上的伪距和相位观测值,ρrs为接收机r到卫星s的几何距离,c为光在真空中的传播速度,dtr和dts为接收机和卫星的钟差,δion为电离层延迟,δtro为对流层延迟,δmuit表示多路径误差,dr, ks和br, ks分别为伪距和相位在k频率上的卫星接收机硬件延迟,λk为相位波长,N为相位模糊度,εP, k和ζL, k分别为伪距和相位的噪声项。
对式(1)中2种信号作差,得到无几何距离组合观测量为:
| $ P_4=P_{\mathrm{r}, i}^{\mathrm{s}}-P_{\mathrm{r}, j}^{\mathrm{s}}=\delta_{\text {ion }, i}-\delta_{\text {ion }, j}+\mathrm{DCB}_{\mathrm{r}}+\mathrm{DCB}^{\mathrm{s}} $ | (3) |
式中,DCBr=dr, i-dr, j、DCBs=dis-djs分别为信号在接收机端和卫星端2个频率的硬件延迟之差。为减少伪距噪声的影响,载波相位用于平滑伪距,同时仅考虑电离层延迟一阶项的影响,得到平滑后的伪距为:
| $ P_{4, \mathrm{sm}}=40.3\left(\frac{1}{f_1^2-f_2^2}\right) \mathrm{STEC}+\mathrm{DCB}_{\mathrm{r}}+\mathrm{DCB}^{\mathrm{s}} $ | (4) |
式中,f1和f2为信号频率,STEC为沿路径的倾斜总电子含量。本文用电离层球谐函数模型对电离层进行建模,得到用于DCB的估计公式为:
| $\begin{gathered} \sum\limits_{n=0}^{n_{\max }} \sum\limits_{m=0}^n \widetilde{P}_{n m}(\sin \beta)\left(a_{n m} \cos m s+b_{m m} \sin m s\right)= \\ \operatorname{MF}(z)\left[-\frac{f_1^2 f_2^2}{40.3\left(f_1^2-f_2^2\right)}\left(P_4-c \mathrm{DCB}_{\mathrm{r}}-c \mathrm{DCB}^{\mathrm{s}}\right)\right] \end{gathered} $ | (5) |
式(5)左侧为电离层球谐函数模型,MF(z)为投影函数。由式(5)可见,估计的结果直接受平滑伪距的影响,其数据质量主要受多路径误差和模型噪声的影响。本文在此基础上通过数学模型定量描述多路径误差和模型噪声,从而减弱其对平滑伪距观测量的影响。
1.2 多路径处理的数学模型通过利用相位和伪距观测的组合提取码观测的多路径延迟进行GNSS数据处理:
| $ \left\{\begin{array}{l} \mathrm{MP}_i\left(t_k\right)=P_i\left(t_k\right)-\eta_{i, j} \lambda_i L_i\left(t_k\right)+ \\ \quad\left(\eta_{i, j}-1\right) \lambda_j L_j\left(t_k\right) \\ \eta_{i, j}=\frac{f_i^2+f_j^2}{f_i^2-f_j^2} \end{array}\right. $ | (6) |
式中,MPi(tk)为多路径误差,tk为历元。式(6)求取的多路径延迟中包含模糊度、硬件延迟等因素,二者可当作常量处理,利用多个历元求平均的方法可有效消除该影响。
通过平滑处理后的多路径中仍包含观测噪声,需要进一步通过正则化方法进行去噪处理[10]。处理后的多路径误差主要包括多路径延迟和随高度角改变的伪距偏差,一般的处理办法是将多路径延迟视为零均值或将两者分开处理。本文通过一步建模的思想对伪距偏差和多路径模型进行处理。
采用以高度角为自变量的多项式模型对去噪后的多路径误差中存在的伪距偏差进行处理,多路径延迟采用AR自回归模型:
| $\left\{\begin{array}{l} \overline{\mathrm{MP}}_k\left(e_i\right)=a_0^k+a_1^k e_i+a_2^k e_i^2+R^k\left(e_i\right)+\varepsilon^k\left(e_i\right) \\ R^k\left(e_i\right)=\sum\limits_{d=1}^q \omega_k^d R^k\left(e_{i-d}\right)+v^k\left(e_i\right) \end{array}\right. $ | (7) |
式中,
通过式(7)可以推出第(i+1)高度角的多路径误差矩阵形式为:
| $ \overline{\bf{M P}}_k\left(e_{i+1}\right)=\boldsymbol{B}\left(e_{i+1}\right) \boldsymbol{a}^k+\boldsymbol{R}^k\left(e_{i+1}\right)+\boldsymbol{\varepsilon}^k\left(e_{i+1}\right) $ | (8) |
式中,
| $\begin{gathered} \boldsymbol{R}^k\left(e_{i+1}\right)=\sum\limits_{d=1}^q \omega_k^d\left[\overline{\bf{M P}}_k\left(e_{i+1-d}\right)-\right. \\ \left.\boldsymbol{B}\left(e_{i+1-d}\right) \cdot a^k\right]+\boldsymbol{\zeta}^k\left(e_{i+1}\right) \end{gathered} $ | (9) |
将式(9)代入式(8)中可以得到:
| $ \begin{gathered} \overline{\bf{M P}}_k\left(e_{i+1}\right)-\sum\limits_{d=1}^q \omega_k^d \cdot \overline{\bf{M P}}_k\left(e_{i+1-d}\right)= \\ \boldsymbol{B}\left(e_{i+1-d}\right) \cdot \boldsymbol{a}^k-\sum\limits_{d=1}^q \omega_k^d \cdot \boldsymbol{B}\left(e_{i+1-d}\right) \cdot \boldsymbol{a}_k \end{gathered} $ | (10) |
处理第k颗卫星n个历元的数据,可以得到第k颗卫星的一步处理方程:
| $\begin{gathered} {\left[\boldsymbol{U}-\left(\boldsymbol{S}_{n-q} \otimes \boldsymbol{\omega}_k^{\mathrm{T}}\right) \cdot N\right] \cdot \overline{\bf{M P}}_k=} \\ {\left[\boldsymbol{A}-\left(\boldsymbol{S}_{n-q} \otimes \boldsymbol{\omega}_k^{\mathrm{T}}\right) \cdot M\right] \cdot \boldsymbol{a}_k} \end{gathered} $ | (11) |
式中,
| $ \begin{gathered} \boldsymbol{U}=\left[\begin{array}{c} \boldsymbol{z}_{q+1}^{\mathrm{T}} \\ \boldsymbol{z}_q^{\mathrm{T}} \\ \vdots \\ \boldsymbol{z}_n^{\mathrm{T}} \end{array}\right], \boldsymbol{Q}_j=\left[\begin{array}{c} \boldsymbol{z}_{j-1}^{\mathrm{T}} \\ \boldsymbol{z}_{j-1}^{\mathrm{T}} \\ \vdots \\ \boldsymbol{z}_{j-1}^{\mathrm{T}} \end{array}\right], \boldsymbol{N}=\left[\begin{array}{c} \boldsymbol{Q}_{q+1} \\ \boldsymbol{Q}_{q+2} \\ \vdots \\ \boldsymbol{Q}_n \end{array}\right], \\ \boldsymbol{A}=\left[\begin{array}{c} \boldsymbol{B}\left(e_{q+1}\right) \\ \boldsymbol{B}\left(e_{q+2}\right) \\ \vdots \\ \boldsymbol{B}\left(e_n\right) \end{array}\right], \boldsymbol{G}_j=\left[\begin{array}{c} \boldsymbol{B}\left(e_{j-1}\right) \\ \boldsymbol{B}\left(e_{j-2}\right) \\ \vdots \\ \boldsymbol{B}\left(e_{j-q}\right) \end{array}\right], \boldsymbol{M}=\left[\begin{array}{c} \boldsymbol{G}_{q+1} \\ \boldsymbol{G}_{q+2} \\ \vdots \\ \boldsymbol{G}_n \end{array}\right] \end{gathered} $ | (12) |
式中,zj为n×n阶单位矩阵的第j列。通过式(8)~(12)可以一步求出多路径延迟项,求得的值可作为观测值改正数用来修正伪距观测值中的偏差和多路径误差,提高观测数据质量,也可用来进行BDS-3的DCB后续估计。
2 实验数据与处理策略 2.1 实验数据为评估各类DCB的准确性和稳定性,将本文估计的DCB与CAS和DLR提供的DCB产品作比较。目前BDS-3可提供的信号频率一共有7种,其中C2I、C6I和C7I播发的时间久且数据质量较好,三者之间的偏差容易被估计。因此,本文仅对BDS-3新频点B1C(1 575.42 mHz)、B2a(1 176.45 mHz)、B2b(1 207.14 mHz)和B2(1 191.795 mHz)产生的频间偏差作估计,其他类型的DCB均可根据上述估计值进行线性组合得到,具体类型和测站个数如表 1所示。本文选取2020-12-01~31(doy 336~366)112个测站数据,测站分布如图 1所示。
|
|
表 1 估计的DCB类型与测站个数 Tab. 1 Estimated DCB types and number of stations |

|
图 1 全球112个MGEX测站分布 Fig. 1 Geographical distribution of 112 MGEX stations |
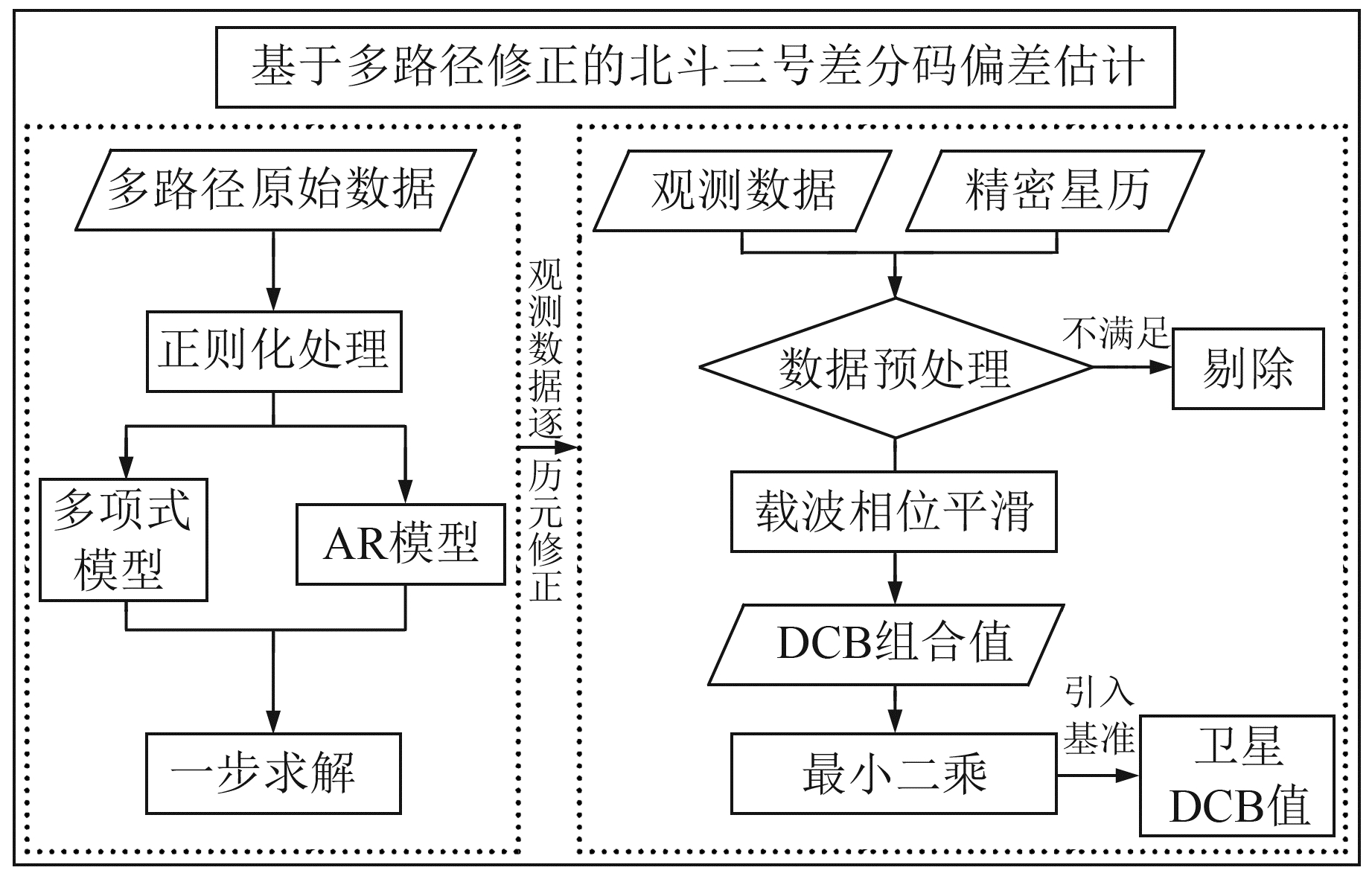
实验处理策略如图 2所示。首先基于原始观测数据求出多路径原始序列,通过正则化、多项式模型和AR模型对序列进行去噪处理,获得纯净的多路径延迟时间序列;然后对观测数据进行多路径逐历元修正,得到的观测值用来估计BDS-3的DCB;最后分别使用CAS的DCB产品和本文估计的DCB进行PPP实验。预处理需要剔除连续观测历元较少的数据,卫星截止高度角为10°,P4平均值阈值设置为30。
|
图 2 基于多路径修正的BDS-3 DCB估计策略 Fig. 2 Estimationstrategy of BDS-3 DCB based on multipath correction |
为减弱多路径延迟对观测数据的影响,需要对多路径延迟量进行分析,并从估值内部闭合差、与CAS和DLR的偏差及月稳定性3个方面评估本文估计DCB的准确性和稳定性。
3.1 BDS-3多路径分析本文选取WUH2和WARN两个跟踪站的观测数据对BDS-3 MEO和IGSO卫星的多路径序列展开研究分析。图 3为WUH2和WARN两个测站的多路径序列,表 2(单位m)和3(单位m)分别为MEO和IGSO卫星的多路径序列均值。由图 3可见,BDS-3存在0~1 m的多路径延迟,低高度角处的多路径延迟较大,多路径延迟随高度角的增大而降低,主要原因是卫星在低高度角处的信噪比较小,观测数据存在很大噪声。从信号角度分析,相比于其他北斗信号,B1I信号的抗多路径能力最差,新频点B2的抗多路径能力最强。由表 2和3可以看出,序列均值为cm级,证明了新频点信号具有抗多路径优越性。在处理序列残差方面,经过正则化处理后的观测数据在处理噪声项方面有一定的效果,但经过一步法方案处理后的结果残差更小,其多路径序列相比之前更加稳定。

|
图 3 不同修正方案下的BDS-3多路径序列 Fig. 3 BDS-3multipath delays with different correction methods |
|
|
表 2 BDS-3 MEO多频信号观测数据不同高度角的多路径原始及修正序列均值 Tab. 2 Multipath original and modified sequence mean of BDS-3 MEO multi frequency signal observation data at different altitude angles |
|
|
表 3 BDS-3 IGSO多频信号观测数据不同高度角的多路径原始及修正序列均值 Tab. 3 Multipath original and modified sequence mean of BDS-3 IGSO multi frequency signal observation data at different altitude angles |
为更好地说明一步法方案修正多路径的普适性,表 4(单位%)列出随机选取的部分卫星经过一步法修正后的RMS提高百分比。由表可见,一步法修正后的卫星多路径序列RMS显著降低,证明此方案具有有效性。经一步法修正后的多路径值可有效消除MP中伪距偏差及多路径延迟误差的影响,剩余的残差项可看作是卫星的多路径延迟改正数,可代入到伪距观测值中提高数据质量。
|
|
表 4 多路径序列修正后RMS提高百分比 Tab. 4 Percentage improvement of the RMS of MP |
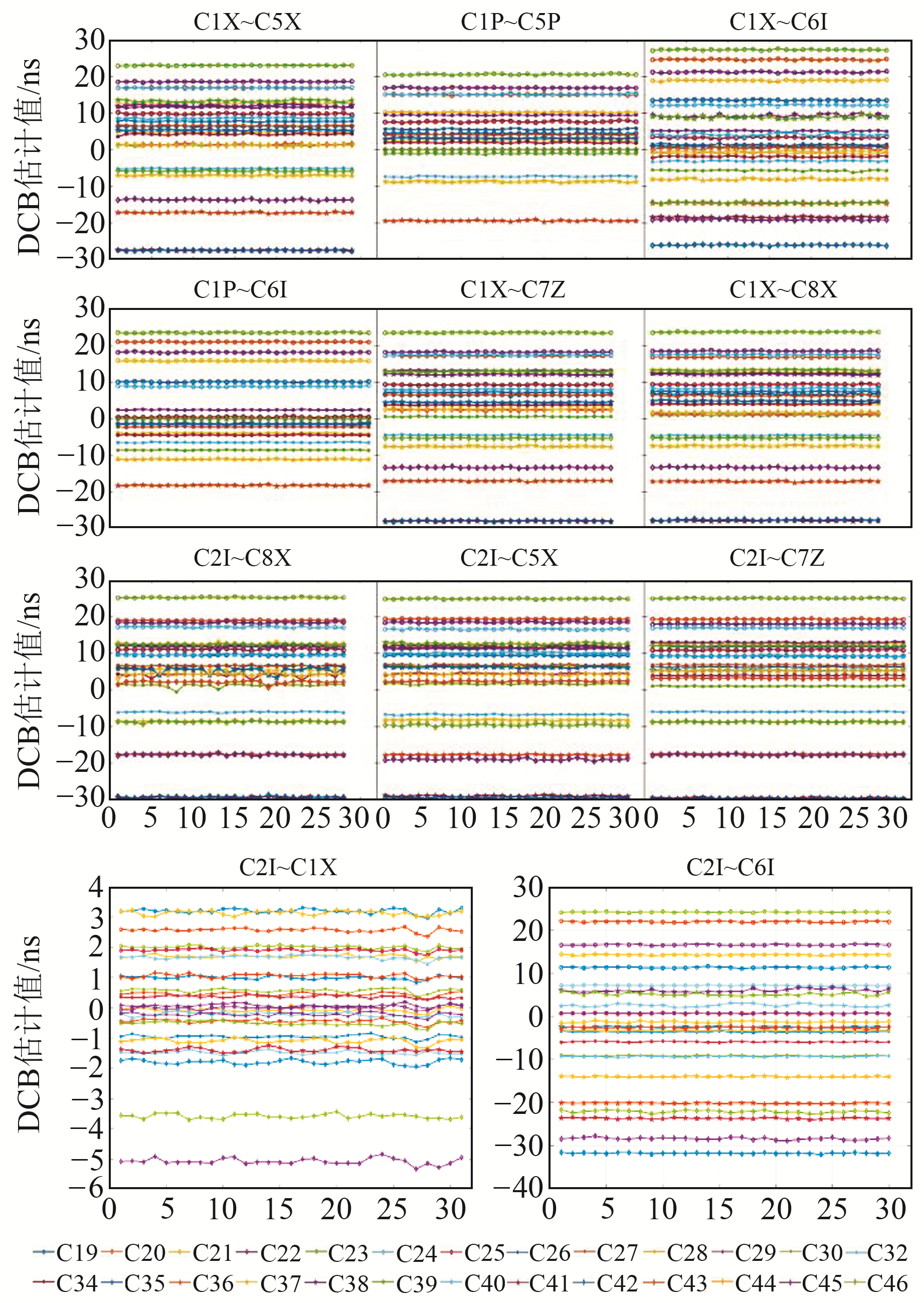
由于DCB在1 d内可以看作是一个常数,因此可以通过月估计值的稳定性来评判估计是否有效。图 4为各卫星(未包括C33)11类DCB的月估计值,由图可见,各卫星C2I~C1X的偏差值分布在-5~5 ns范围内,相比于其他类型的伪距DCB值而言较小;剩余10类DCB值分布在-30~30 ns范围内,部分卫星DCB值较大,其中C35号卫星DCB值较大,必须对其进行估计和修正,否则会对定位精度产生较大影响。11类DCB月估计值都趋于稳定,证明了估计方案的有效性。
|
图 4 BDS-3号各卫星11类DCB估计值时间序列 Fig. 4 Time series of eleven kinds of DCB estimates of BDS-3 satellites |
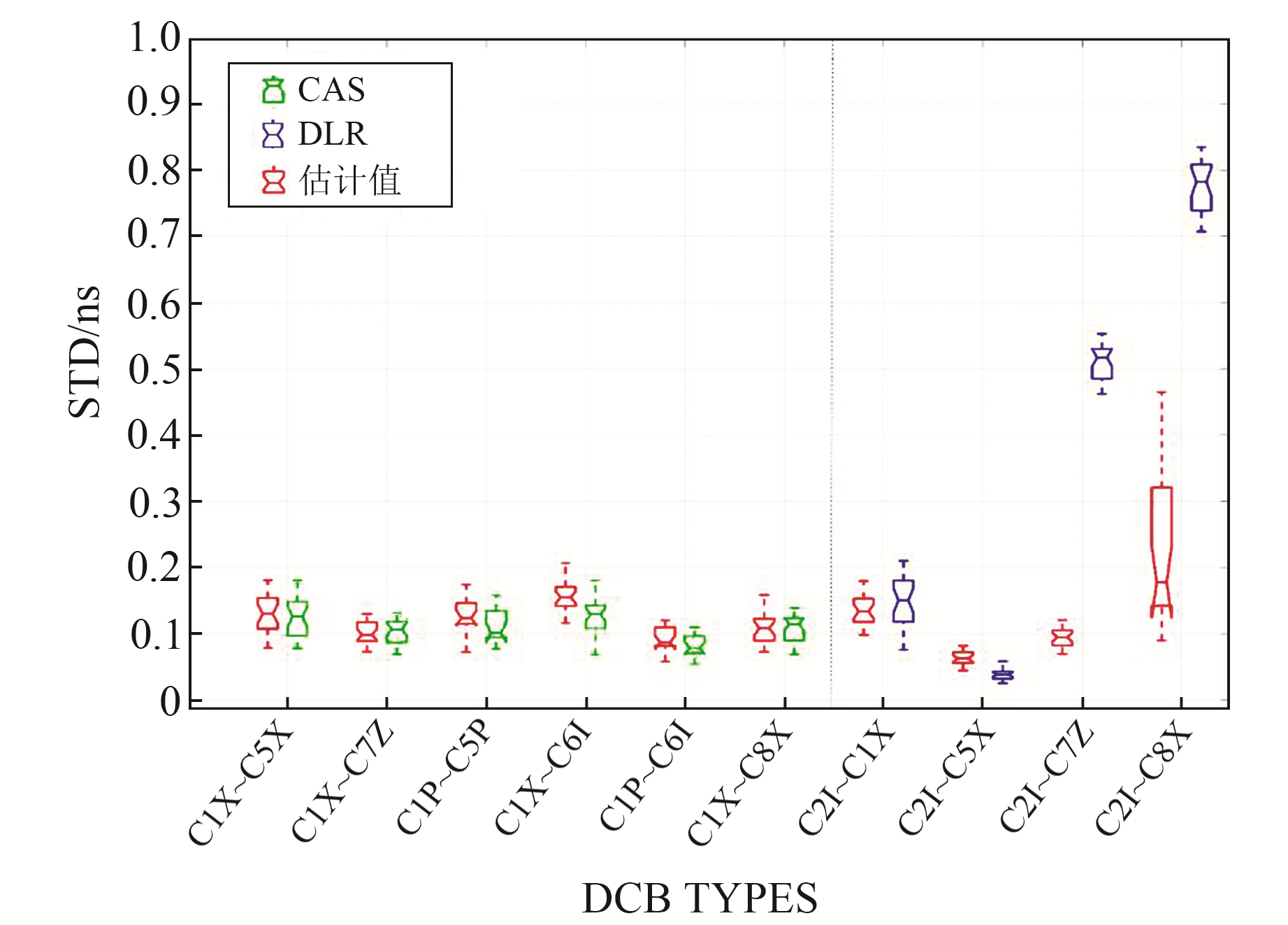
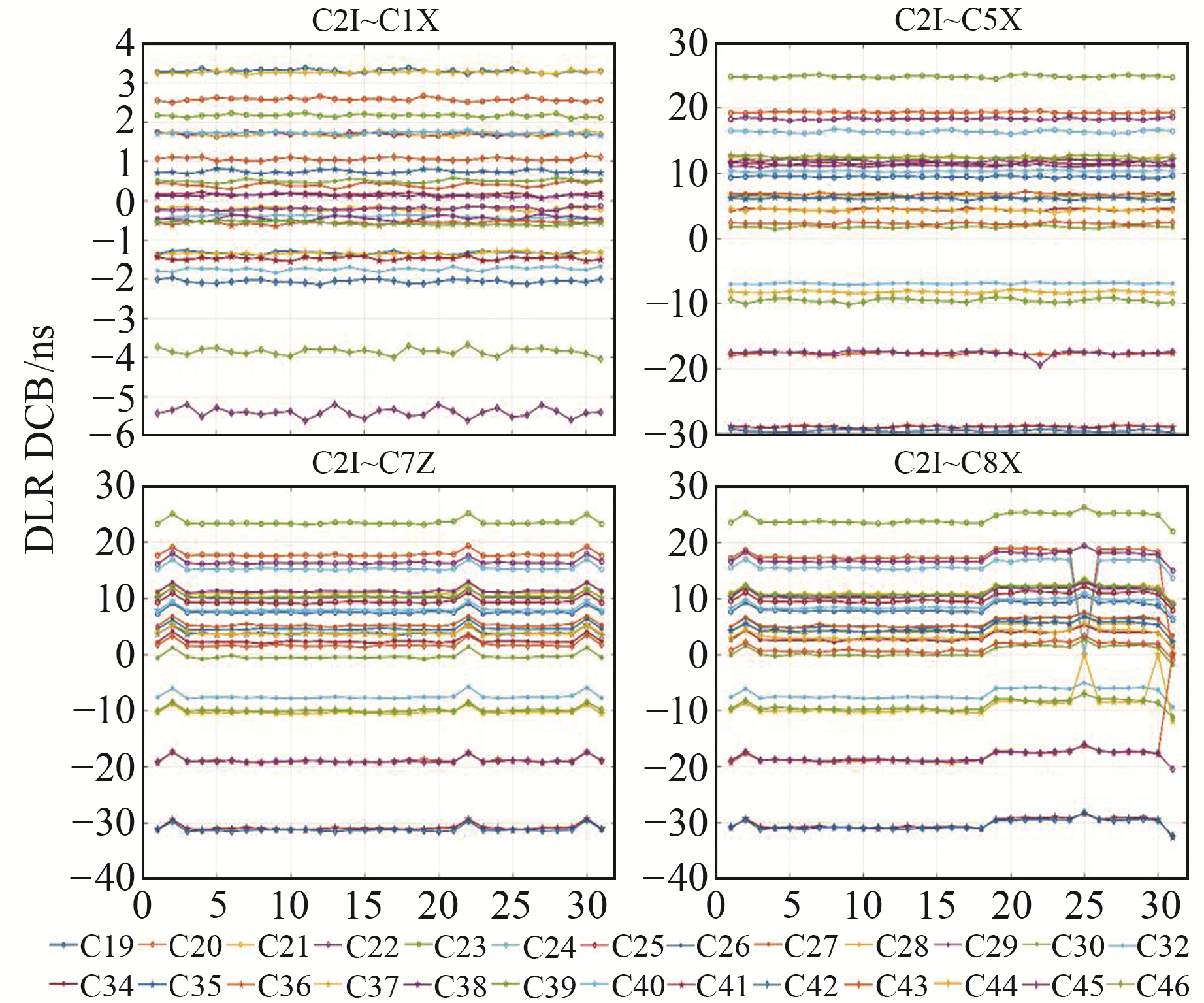
图 5为10类DCB估计值的STD箱线图,表 5(单位ns)为DCB产品的月STD均值。由图 5和表 5可见,各类DCB产品的STD值都在1 ns范围内,CAS提供的7类DCB产品的STD值与本文估计值相当。将本文估计值与DLR产品对比发现,C2I~C1X和C2I~C5X偏差的STD值基本一致,C2I~C7Z和C2I~C8X两类DCB的STD值相差较大。主要原因为能接收B2b和B2两种信号的测站个数较少,观测数据质量较差。图 6为DLR 4类DCB产品1个月的时间序列,可以看出,C2I~C1X和C2I~C5X没有出现较大波动,而C2I~C7Z和C2I~C8X分别在第2、22、30 d和第2、19、25、30 d出现1 ns的波动,主要因为这些时段有卫星未参与解算,导致解算基准发生改变,使得当天数据出现跳动。
|
图 5 10类DCB的STD值 Fig. 5 STD of ten DCB |
|
|
表 5 北斗卫星DCB的月STD均值 Tab. 5 Monthly mean STD of BDS satellite DCBs |
|
图 6 DLR 4种DCB产品时间序列 Fig. 6 Time series of four DLR DCB products |
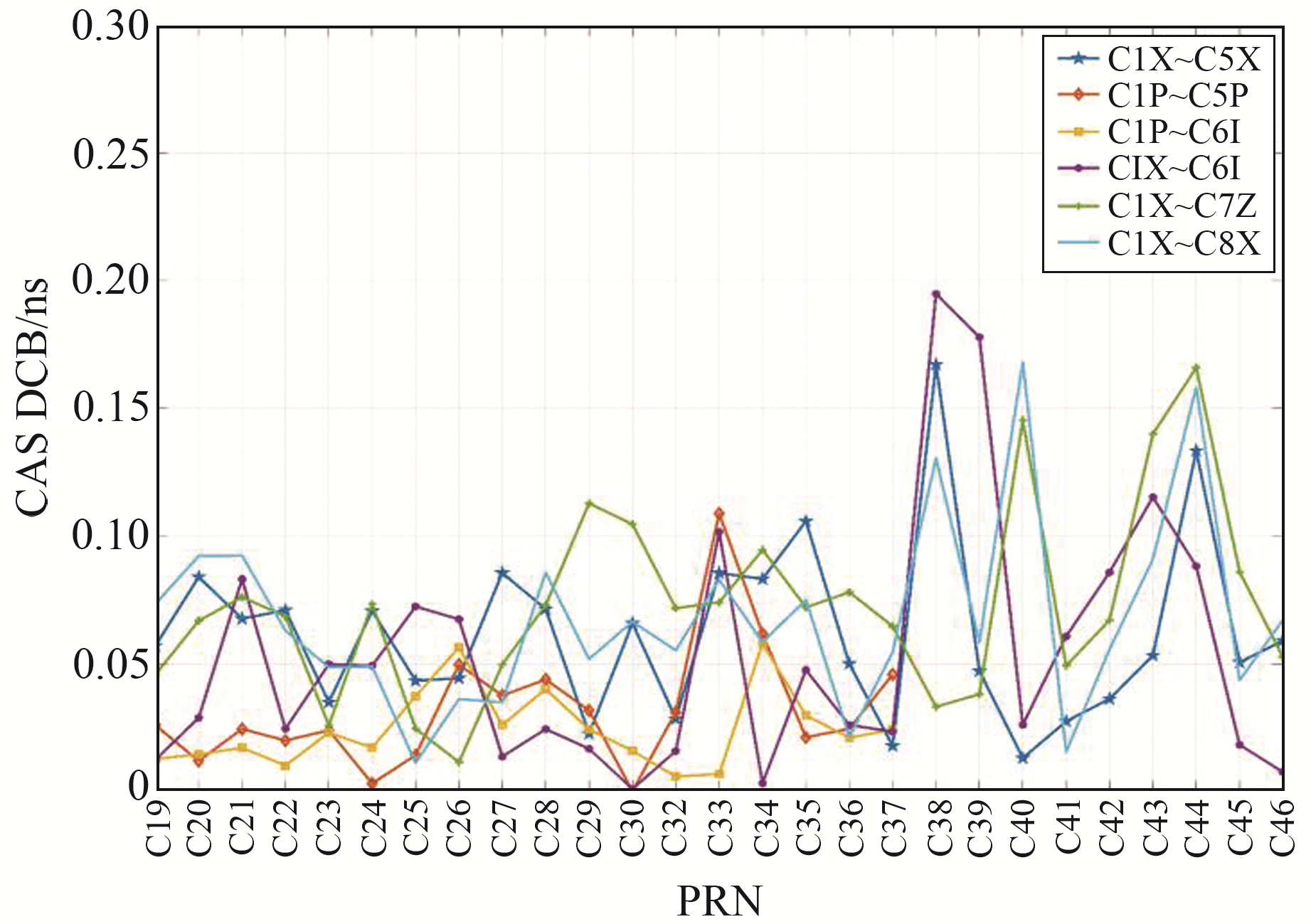
图 7为估计值与6类CAS提供的产品的差值,由图可知,偏差基本在0.1 ns范围内波动,其中C1X~C6I的C38号卫星偏差达到0.18 ns,这主要与观测数据质量有关。总体对比分析后可知,本文DCB估计值的精度与CAS提供的DCB产品精度一致。
|
图 7 估计值与CAS的6种DCB产品月平均偏差 Fig. 7 Monthly average deviation between six estimates and CASDCB products |
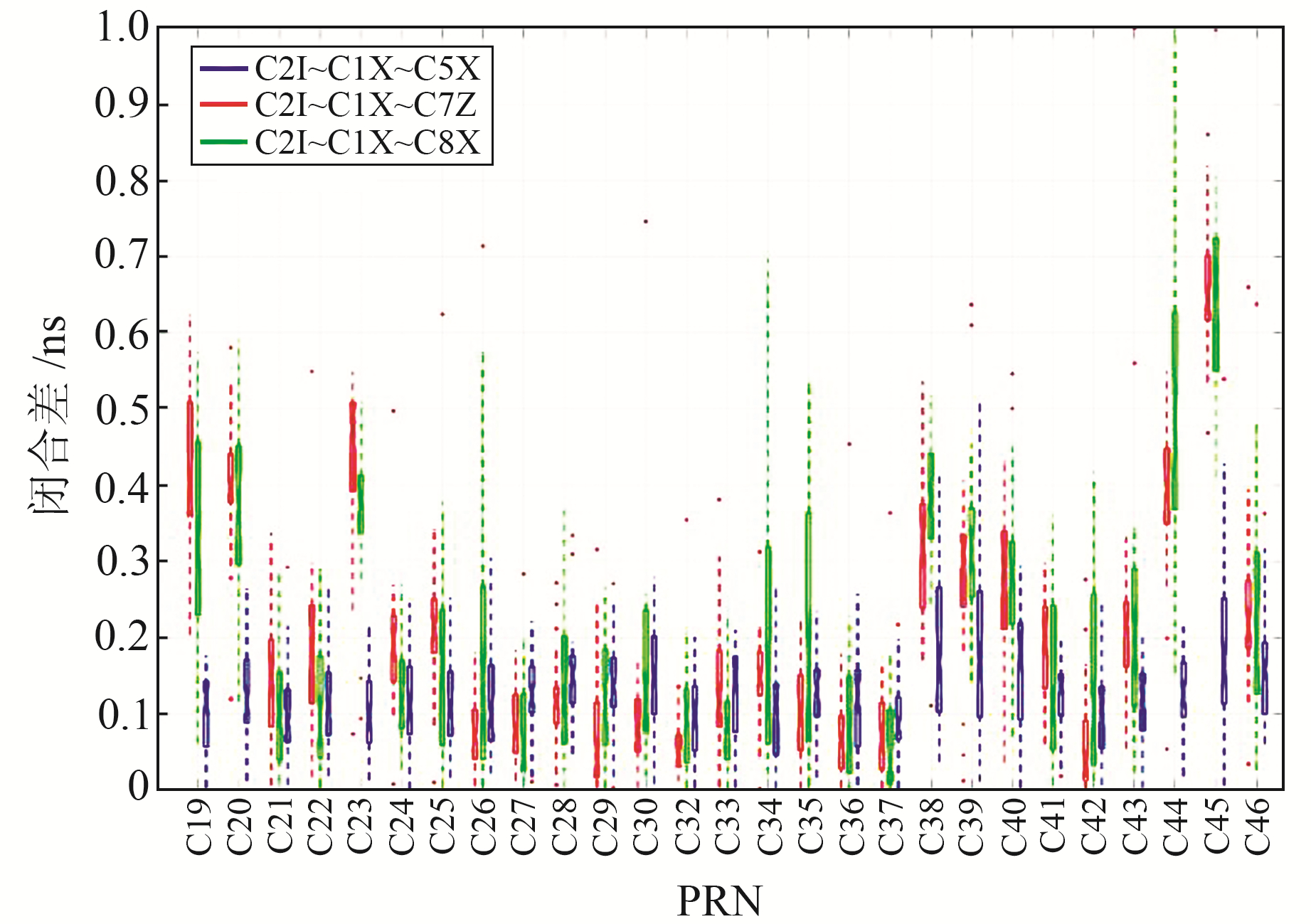
由§3.2和§3.3可知,由于可接收B2b和B2信号的测站个数较少,且DLR部分产品有1 ns的波动,导致数据质量较差,因此本文对4类DCB(C2I~C1X、C2I~C5X、C2I~C7Z和C2I~C8X)进行补充分析。本文分析C2I~C1X~C5X、C2I~C1X~C7Z和C2I~C1X~C8X的闭合差,理论上3个DCB之间的闭合差为0。图 8为各卫星3种闭合差的箱线图,表 6(单位ns)为各卫星每种闭合差的最小值、最大值及中值。由图 8和表 6可知,3种DCB闭合差中值分别为0.127 2 ns、0.206 3 ns和0.200 1 ns,其中C2I~C1X~C5闭合差在0.01~0.382 ns范围内波动,而C2I~C1X~C7Z和C2I~C1X~C8X的部分卫星闭合差出现较大值,如C45号卫星C2I~C1X~C7Z闭合差达0.62 ns、C2I~C1X~C8X闭合差达0.66 ns。分析C45号卫星C2I~C7Z和C2I~C8X的STD值可知,C2I~C8X的STD值达0.368 4 ns,C2I~C7Z的STD值达0.167 7 ns,相比于其他卫星而言更加离散。
|
图 8 BDS-3各卫星3种闭合差分布 Fig. 8 Three closing error distributions of BDS-3 satellites |
|
|
表 6 BDS-3各卫星3种闭合差指标平均值统计 Tab. 6 BDS-3statistics of the average of three closure error indexes of each satellite |
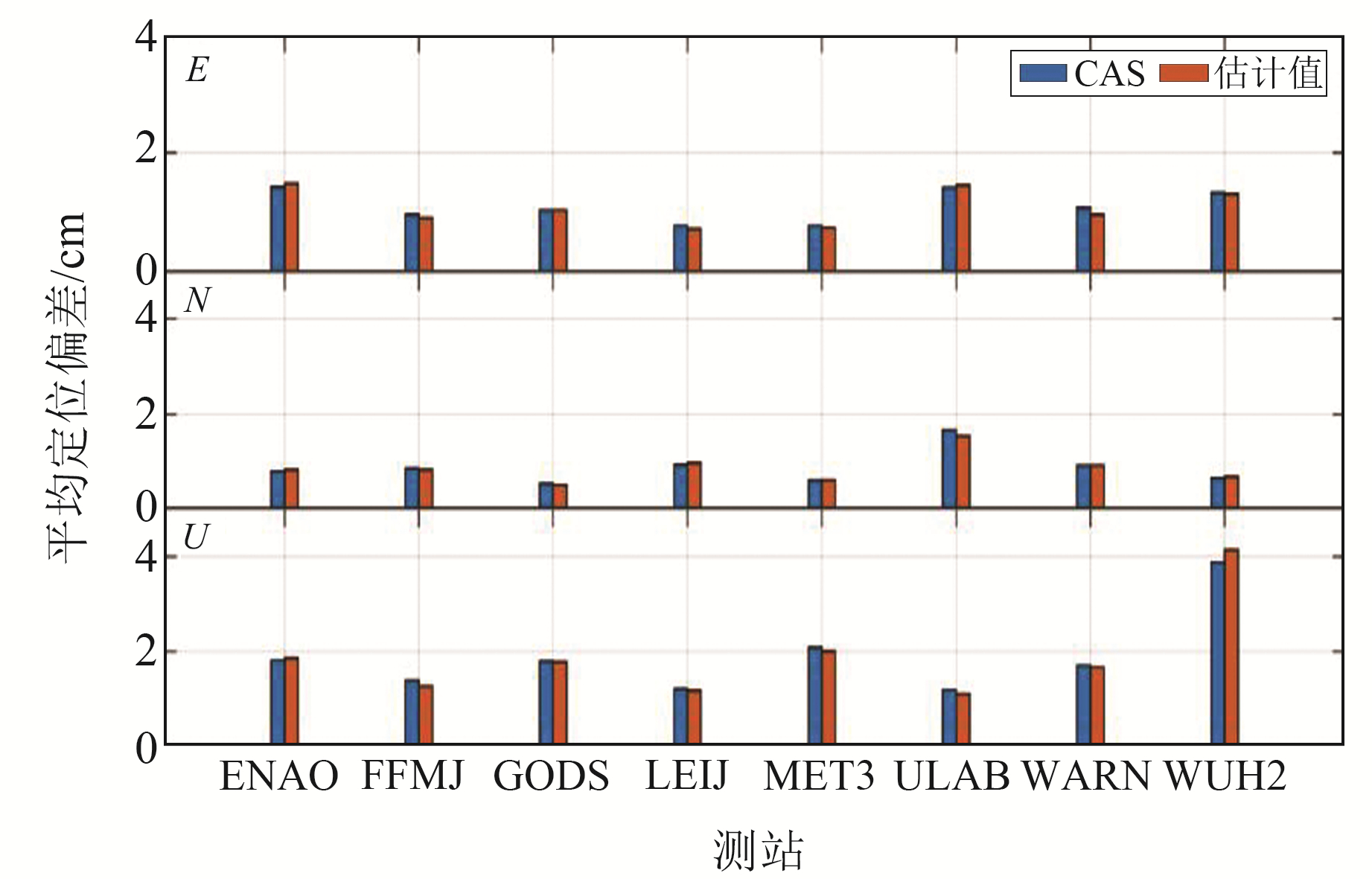
为比较本文估计的DCB对PPP的影响,选用ENAO、FFMJ、GODS、LEIJ、MET3、ULAB、WARN、WUH2等8个测站2020-12-18~24陆态网跟踪站30 s观测数据进行静态PPP实验[12-13]。实验所用DCB改正分为2种,即本文估计的DCB改正和CAS提供的DCB产品改正。DCB产品选取的是BDS-3 B1I和B3I两个频率的组合,8个测站连续1周的静态PPP平均偏差结果如图 9所示。
|
图 9 8个测站2种DCB改正静态PPP精度偏差 Fig. 9 The average values of dynamic positioning deviation of two DCB correction methods at 8 stations |
从图 9可以看出,不同测站不同DCB改正的静态PPP精度各有优势,但改正效果相当,表 7(单位cm)为2种DCB改正的8个测站静态PPP精度RMS值及收敛时间均值,当测站E、N、U三方向的绝对定位误差连续60个历元(30 min)均小于0.1 m时判定为收敛。由表 7可见,结果并未表现出一致性,部分测站利用本文估计的DCB改正定位的精度和收敛时间优于CAS提供的产品,如FFMJ测站在E、N、U三方向的精度分别提高6.2%、12.8%、9.8%,收敛时间提高5.1%;而ENAO和WUH2测站却没有表现出这一特点。综上可知,本文估计的DCB与CAS提供的产品性能相当。
|
|
表 7 8个测站2种DCB处理策略下PPP定位平均RMS值及收敛时间 Tab. 7 Average RMS value and convergence time of precision single point positioning under two DCB processing strategies of 8 stations |
1) BDS-3多路径在低高度角处误差较大,约为1 ns;B2信号抗多路径能力最好,B1I最差。经过一步法处理后的多路径序列更加稳定,证明伪距偏差的多项式模型和多路径误差的AR模型具有有效性。
2) 利用经多路径处理后的伪距观测数据估计的11类DCB值月稳定性较好,未出现较大波动;估计的DCB与CAS的偏差在0.1 ns范围内,精度较高;各卫星3种DCB闭合差分布在0.2 ns以内,具有较高的内符合精度。
3) 由于DLR产品存在有卫星不参与解算的情况,因此在求解时应注意基准的变换,而CAS产品相对于DLR产品更加稳定。
4) 本文估计的DCB和CAS提供的产品性能相当。
本文对于B2b和B2信号的处理策略有待提高,未来会继续跟进对BDS-3新频信号差分码偏差的研究。后续将重点研究绝对码偏差OSB在GNSS绝对码偏差估计中的应用。
| [1] |
Wang N B. Study on GNSS Differential Code Biases and Global Broadcast Ionospheric Models of GPS, Galileo and BDS[J]. Acta Geodaetica et Cartographica Sinica, 2017
(  0) 0) |
| [2] |
张宝成, 欧吉坤, 袁运斌, 等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报, 2011, 40(4): 447-453 (Zhang Baocheng, Ou Jikun, Yuan Yunbin, et al. Calibration of Slant Total Electron Content and Satellite-Receiver's Differential Code Biases with Uncombined Precise Point Positioning Technique[J]. Acta Geotaetica et Cartographica Sinica, 2011, 40(4): 447-453)
(  0) 0) |
| [3] |
谷世铭, 党亚民, 王虎, 等. 北斗差分码偏差改正对单点定位的影响[J]. 测绘科学, 2020, 45(10): 10-15 (Gu Shiming, Dang Yamin, Wang Hu, et al. The Effect of Beidou DCB Correction on Single Point Positioning[J]. Science of Surveying and Mapping, 2020, 45(10): 10-15)
(  0) 0) |
| [4] |
王利军, 焦文海, 贾小林, 等. BDS-3精密单点定位性能比较分析[J]. 大地测量与地球动力学, 2021, 41(4): 357-361 (Wang Lijun, Jiao Wenhai, Jia Xiaolin, et al. Comparative Analysis of BDS-3 Precise Point Positioning Performance[J]. Journal of Geodesy and Geodynamics, 2021, 41(4): 357-361)
(  0) 0) |
| [5] |
吴竞, 唐成盼, 周善石, 等. BDS-2导航电文的TGD参数精度及其对用户导航定位精度的影响[J]. 天文学进展, 2019, 37(3): 337-346 (Wu Jing, Tang Chengpan, Zhou Shanshi, et al. TGD Parameter Accuracy of BDS-2 Navigation Message and Its Influence on User Navigation and Positioning Accuracy[J]. Progress in Astronomy, 2019, 37(3): 337-346)
(  0) 0) |
| [6] |
邓远帆, 郭斐, 张小红, 等. 北斗三号卫星多频多通道差分码偏差估计与分析[J]. 测绘学报, 2021, 50(4): 448-456 (Deng Yuanfan, Guo Fei, Zhang Xiaohong, et al. Estimation and Analysis of the Multi-Frequency and Multi-Channel DCB for BDS-3[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(4): 448-456)
(  0) 0) |
| [7] |
Hu C, Wang Z Y, Rao P W, et al. One-Step Correction Strategy for BDS-2/BDS-3 Satellite Observation Code Bias and Multipath Delay[J]. Acta Geodaetica et Geophysica, 2021, 56(1): 29-59
(  0) 0) |
| [8] |
Chang G B, Chen C, Yang Y X, et al. Tikhonov Regularization Based Modeling and Sidereal Filtering Mitigation of GNSS Multipath Errors[J]. Remote Sensing, 2018, 10(11): 1 801
(  0) 0) |
| [9] |
胡超. BDS-2/BDS-3卫星观测数据联合处理关键技术研究[D]. 徐州: 中国矿业大学, 2020 (Hu Chao. An Investigation of Key Technologies Related to Combining BDS-2 and BDS-3 Observations in Data Processing[D]. Xuzhou: China University of Mining and Technology, 2020)
(  0) 0) |
| [10] |
罗廷金. 基于稀疏优化的学习方法及应用研究[D]. 长沙: 国防科技大学, 2018 (Luo Tingjin. Research on Learning Models Based on Sparse Optimization and Their Applications[D]. Changsha: National University of Defense Technology, 2018.)
(  0) 0) |
| [11] |
吴飞. 几种改进的地球自转参数预报方法[D]. 徐州: 中国矿业大学, 2019 (Wu Fei. Several Improved Methods for Prediction of Earth Rotation Parameters[D]. Xuzhou: China University of Mining and Technology, 2019)
(  0) 0) |
| [12] |
周锋. 多系统GNSS非差非组合精密单点定位相关理论和方法研究[D]. 上海: 华东师范大学, 2018 (Zhou Feng. Theory and Methodology of Multi-GNSS Undifferenced and Uncombined Precise Point Positioning[D]. Shanghai: East China Normal University, 2018)
(  0) 0) |
| [13] |
吴志远, 王潜心, 胡超, 等. BDS-3多频PPP模型性能分析[J]. 大地测量与地球动力学, 2022, 42(8): 846-851 (Wu Zhiyuan, Wang Qianxin, Hu Chao, et al. Performance Analysis of BDS-3 Multi-Frequency PPP Model[J]. Journal of Geodesy and Geodynamics, 2022, 42(8): 846-851)
(  0) 0) |
2. School of Spatial Information and Geomatics Engineering, Anhui University of Science and Technology, 168 Taifeng Street, Huainan 232001, China
 2023, Vol. 43
2023, Vol. 43

