2. 中国地质大学(武汉)地理与信息工程学院,武汉市鲁磨路388号,430079;
3. 武汉大学卫星导航定位技术研究中心,武汉市珞喻路129号,430079
火星是类地行星,具有与地球相近的“黄赤交角”和自转周期,也存在岁差、章动与极移等现象[1]。和地球极移一样,火星极移是指火星自转轴相对于火星参考系极轴的运动,与火星的内核运动及表面季节性变化有关。通过对火星极移时间序列各周期项进行研究,可以更加深入地了解火星液核、地幔等结构及火星大气、潮汐运动的特征与规律。而对火星极移进行预报,则可以为火星探测器的精密定轨及着陆器的定位提供所需的定向参数,对太阳系起源与演化研究及人类航天事业发展都有着十分重要的意义[2]。
目前对火星定向参数的研究仍是将地球自转运动的各项结果拓展到火星上[3],而对于火星极的空间运动,既可以用理论进行模拟,也需要用由火星探测获得的数据资料进行约束[4]。将火星极运动的理论值与由火星探测得到的观测值进行比较,是检验当下火星模型的重要手段,也是为改进与火星定向参数有关的各项理论提供依据的有效途径。因此,开展火星极移参数预报模型的相关研究至关重要。
本文首先利用NASA提供的NP.ang和NP.ds火星极移序列进行时变分析与预报,并分别利用自回归滑动平均(autoregressive moving average model,ARMA)模型和ARIMA模型对NP.ds进行短期预报实验;再利用最小二乘外推模型对NP.ds进行中长期预报实验,在对离散傅里叶变换结果进行分析后,改进用于拟合的周期项数值,以实现更高精度的中长期预报。
1 星历数据及处理 1.1 Horizons System简介本文采用的星历数据来自于NASA喷气推进实验室太阳系动力学小组提供的Horizons System。Horizons System是一个在线太阳系数据和星历计算服务系统,可以向用户提供对太阳系关键数据的访问途径,还可以针对太阳系内的对象灵活生成高精度星历表,这些对象包括1 204 271颗小行星、3 794颗彗星、211颗行星的卫星(包括地球的卫星及矮行星冥王星)、太阳、太阳系内全部8颗行星、经过挑选的航天器、拉格朗日点L1、L2及太阳系质心等[5]。
1.2 星历数据预处理由于本文需要对得到的火星极移数据时间序列进行离散傅里叶变换,以提取其中的周期项,因此需要尽可能多地获取火星极移数据,以提高离散傅里叶变换结果的精度。本文获取公元1600-01-02~2500-01-01长达900 a的星历数据,数据步长设置为1 d。
由于本文的研究对象为火星极移的时间序列,历表设置选定的星历数据类型均为与火星北极位置变化有关的数据类型,包括NP.ang和NP.ds。其中,NP.ang指在数据输出时刻的火星北极位置角(即相对于真北天极方向的角度,单位(°)),NP.ds指在数据输出时刻火星北极与火星视中心的角距(单位(″))。
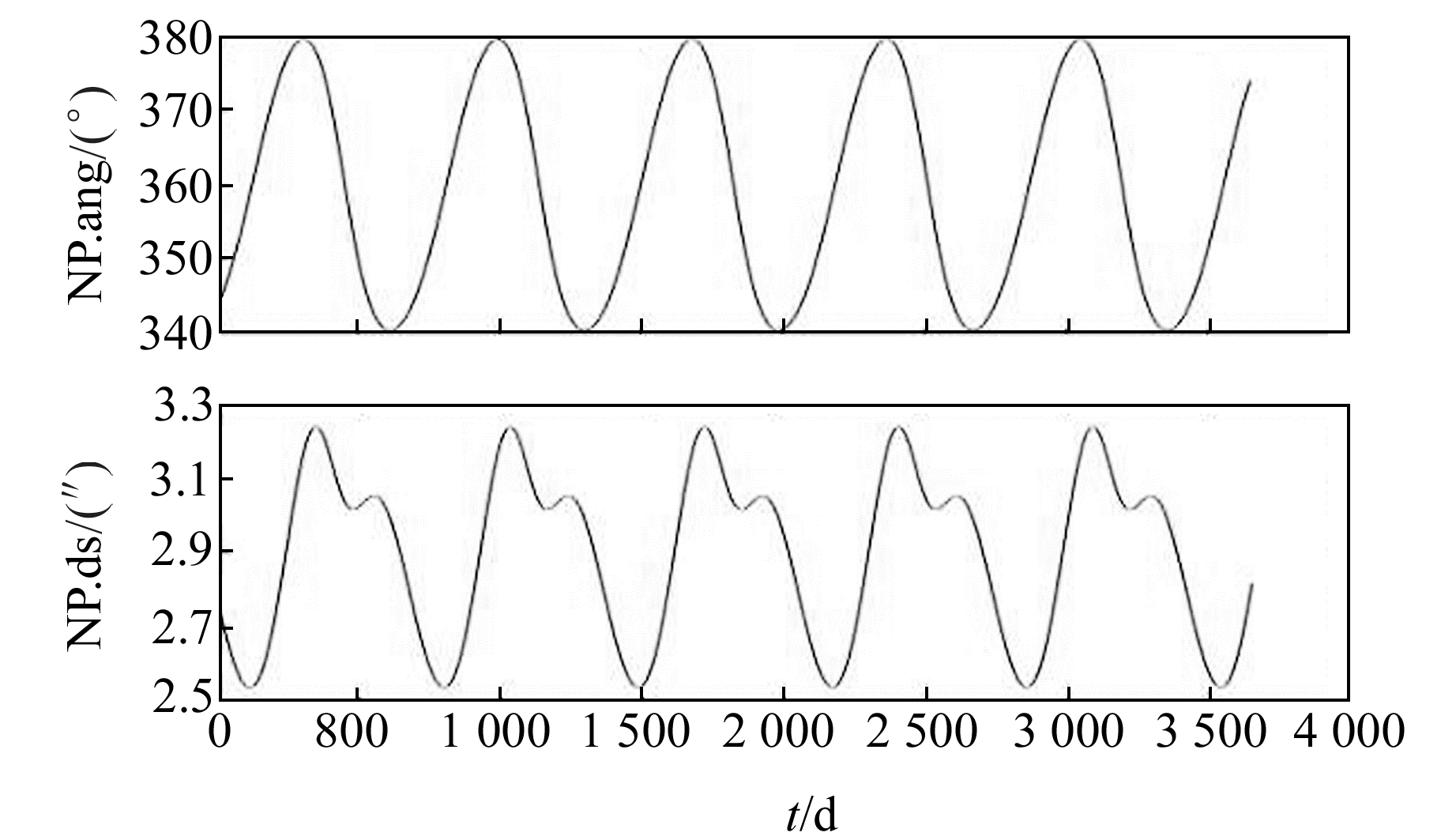
通过观察原始星历数据时间序列发现,NP.ang和NP.ds存在跳变现象。在查阅Horizons System关于输出数据类型的介绍后了解到,NP.ang的跳变是因为该时刻北极位置角小于0°,由于系统没有设定负角度,位置角会被自动加上360°。而NP.ds的跳变是因为当火星北极位于远离观测者的那部分半球时,其与视中心的角距将变为负值[6]。为方便后续时变分析与预报计算,对这2组数据中发生跳变的部分进行相应处理,结果如图 1所示。
|
图 1 1600~1610年NP.ang和Np.ds时间序列 Fig. 1 Np.ang and Np.ds time series from 1600 to 1610 |
离散傅里叶变换利用测量到的原始信号,以累加的方式计算该信号中不同正弦波信号的频率、振幅和相位,最终得到的频谱图中振幅大的频率代表周期性强。
离散傅里叶变换的定义如式(1)所示,其中k为分析的特定采样次数。虽然理论上离散周期信号的频谱是无穷多的,但由于傅里叶级数具有周期性,一般只取主值区间0≤k < N-1进行研究,N为参考的采样点数,i为虚数单位,x(n)为每次观测得到的极移分量数据。将离散傅里叶级数展开后可得式(2):
| $ X(k)=\sum\limits_{n=0}^{N-1} x(n) \mathrm{e}^{-\mathrm{i} \frac{2 \pi}{N} n k} $ | (1) |
| $\begin{gathered} X(k)=\sum\limits_{n=0}^{N-1} x(n) \cos \left(2 \pi \frac{k n}{N}\right)- \\ \mathrm{i} \sum\limits_{n=0}^{N-1} x(n) \sin \left(2 \pi \frac{k n}{N}\right) \end{gathered} $ | (2) |
N个采样点经离散傅里叶变换后的结果为N个复数,每个复数对应1个频率(第n≤N/2个点对应的频率为(n-1)/Nfs),该复数的模值表示该频率的振幅特征。为提取周期项,需要求出相关参数频率和幅值,频率计算公式见式(3),式中,fs为采样频率:
| $ f_k=\frac{k}{N} f_s $ | (3) |
快速傅里叶变换(FFT)是指计算机高效、快速计算离散傅里叶变换(DFT)的方法。离散傅里叶变换实现时间的复杂度为O(n2),而快速傅里叶变换时间复杂度缩小到了O(nlogn)。
2.2 周期项结果与分析通过使用C#语言编写FFT程序,分别对NP.ang与NP.ds的时间序列进行处理,得到2组数据的频谱(图 2)。

|
图 2 NP.ang和NP.ds频谱 Fig. 2 NP.ang and NP.ds spectrum diagrams |
通过图 2可以发现,存在5个较为明显的周期项,其对应的频率、周期及幅值如表 1所示。
|
|
表 1 NP.ang和Np.ds周期项统计 Tab. 1 Np.angand Np.ds period item statistics |
由表 1可见,NP.ang与NP.ds的周期项长度基本一致,且与火星年具有很强的相关性:第1组周期项的周期接近1个火星年,第2组周期项接近0.5个火星年,第3组接近1/3个火星年,第4组接近1/4个火星年,第5组则接近1/5个火星年。假设在没有火星极移的情况下,即在火星北极严格指向平北天极的情况下,火星北极点在ICRS/J2000框架下的太阳系质心惯性坐标为(X, Y, Z),火星圆盘视中心坐标为(XC, YC, ZC),火星质心到太阳系质心的距离减去火星赤道半径为R,则NP.ds(记为θ)满足公式:
| $\begin{gathered} \theta= \\ \frac{180 \times\left[\left(X_C-X\right)^2+\left(Y_C-Y\right)^2+\left(Z_C-Z\right)^2\right]^{\frac{1}{2}}}{\pi R} \end{gathered} $ | (4) |
由于火星公转轨道是椭圆轨道,太阳系质心位于椭圆轨道的一个焦点上,这使得R存在因公转造成的周期性变化(周期为1个火星年,约687 d)。在不考虑极移的情况下,影响NP.ds周期性变化的因素只有R的周期性变化。也就是说,如果不存在极移,NP.ds的时间序列应当有且仅有长度为1个火星年的周期项。同样,在不考虑火星极移的情况下,NP.ang也只与R的周期性变化相关,其时间序列也应当有且仅有长度为1个火星年的周期项。然而,排除掉NP.ang与NP.ds时间序列中接近1个火星年的周期项后,仍存在4个较为明显的周期项(表 2),由此可以认定这些周期项应当与火星极移有关。
|
|
表 2 可能包含极移信息的周期项 Tab. 2 Period item that may contain pole motion information |
通过查阅与火星定向参数,尤其是火星极移有关的文献资料了解到,火星极移主要由两部分组成:其一是季节性变化项,主要和火星大气与其表面质量交换等原因导致的自转角动量变化有关;其二是与地球极移相似的钱德勒(Chandler)摆动,这是非刚体火星的自由摆动,与火星的自由核章动(周期约为230 d,接近1/3个火星年)有关[7]。因此,火星极移参数可表示为:
| $ \begin{aligned} & X_p=\sum\limits_{m=1}^5\left(X_{c m} \cos \left(2 \pi f_m t\right)+X_{s m} \sin \left(2 \pi f_m t\right)\right) \\ & Y_p=\sum\limits_{m=1}^5\left(Y_{c m} \cos \left(2 \pi f_m t\right)+Y_{s m} \sin \left(2 \pi f_m t\right)\right) \end{aligned} $ | (5) |
式中,前4项的fm=m/687代表由火星季节性变化导致的极移变化频率,而最后1项f5表示火星钱德勒摆动的频率[8]。据此可以确定,表 2中前3项均为对应季节性变化项。
3 火星极移预报 3.1 短期预报模型 3.1.1 ARMA模型自回归滑动平均(ARMA)模型是以自回归(AR)模型与滑动平均(MA)模型为基础混合得到的模型,其中AR模型是变量对变量自身的滞后期项进行的回归。具体来说,p阶自回归模型(AR(p))的当期值Yt满足方程:
| $ Y_t=\varphi_1 Y_{t-1}+\varphi_2 Y_{t-2}+\cdots+\varphi_p Y_{t-p}+e_t $ | (6) |
即Yt为距离t期最近的p阶滞后项与随机扰动et的线性组合,其中et包括了被拟合的平稳序列在t期无法用过去值来解释的所有新信息。
而MA模型是将时间序列写成一系列不相关的随机变量线性组合。具体地讲,q阶自回归模型(MA(q))的当期值Yt满足方程:
| $Y_t=\mu+e_t-\theta_1 e_{t-1}-\theta_2 e_{t-2}-\cdots-\theta_q e_{t-q} $ | (7) |
即Yt与以前各期的序列值无关,而是基于前q期随机扰动et-1、et-2、…、et-q的线性回归模型。式中,μ为被拟合的平稳序列均值。
ARMA模型综合了二者的特点。阶数分别为p和q的自回归滑动平均模型(ARMA(p, q))的当期值Yt满足方程:
| $\begin{gathered} Y_t=\varphi_1 Y_{t-1}+\varphi_2 Y_{t-2}+\cdots+\varphi_p Y_{t-p}+ \\ e_t-\theta_1 e_{t-1}-\theta_2 e_{t-2}-\cdots-\theta_q e_{t-q} \end{gathered} $ | (8) |
即当期值Yt不仅与滞后项有关,还与随机扰动有关。
ARMA模型阶数的确定主要通过计算平稳序列的自相关系数(ACF)与偏自相关系数(PACF),并生成对应的序列自相关图与偏自相关图,根据两幅图中系数开始衰减的滞后期数来确定ARMA模型的阶数。
3.1.2 ARIMA模型差分整合移动平均自回归(ARIMA)模型的基本思想与ARMA模型相似:首先假定预测对象随时间的推移形成的数据与其过去的数据有关,这样就可以建立自回归模型及滑动平均模型,并将模型外推来进行预报。对于非平稳时间序列,ARIMA模型会采用差分方法使其显示出平稳的性质,再用于拟合与预报。
ARIMA模型具有3个参数,即在ARMA模型的基础上增加了代表时间序列从非平稳序列变为平稳序列所要进行的差分阶数d[9],对应的ARIMA模型可记为ARIMA(p, d, q),其中AR项p与MA项q的确定方法与ARMA模型类似,而差分阶数d则需要通过ADF检验与KPSS检验来确定。
3.1.3 短期预报考虑到本文使用的星历数据是JPL通过对火星卫星的数值进行积分,并使用地球观测数据和火星探测器影像观测数据进行拟合得来的,过晚或过早时期的星历数据不宜作为预报的拟合值,应采用与开展火星定向参数观测任务相近时期的星历数据,故本文短期预报部分采用2000-01-02~2010-01-01星历数据,共计3 653 d。
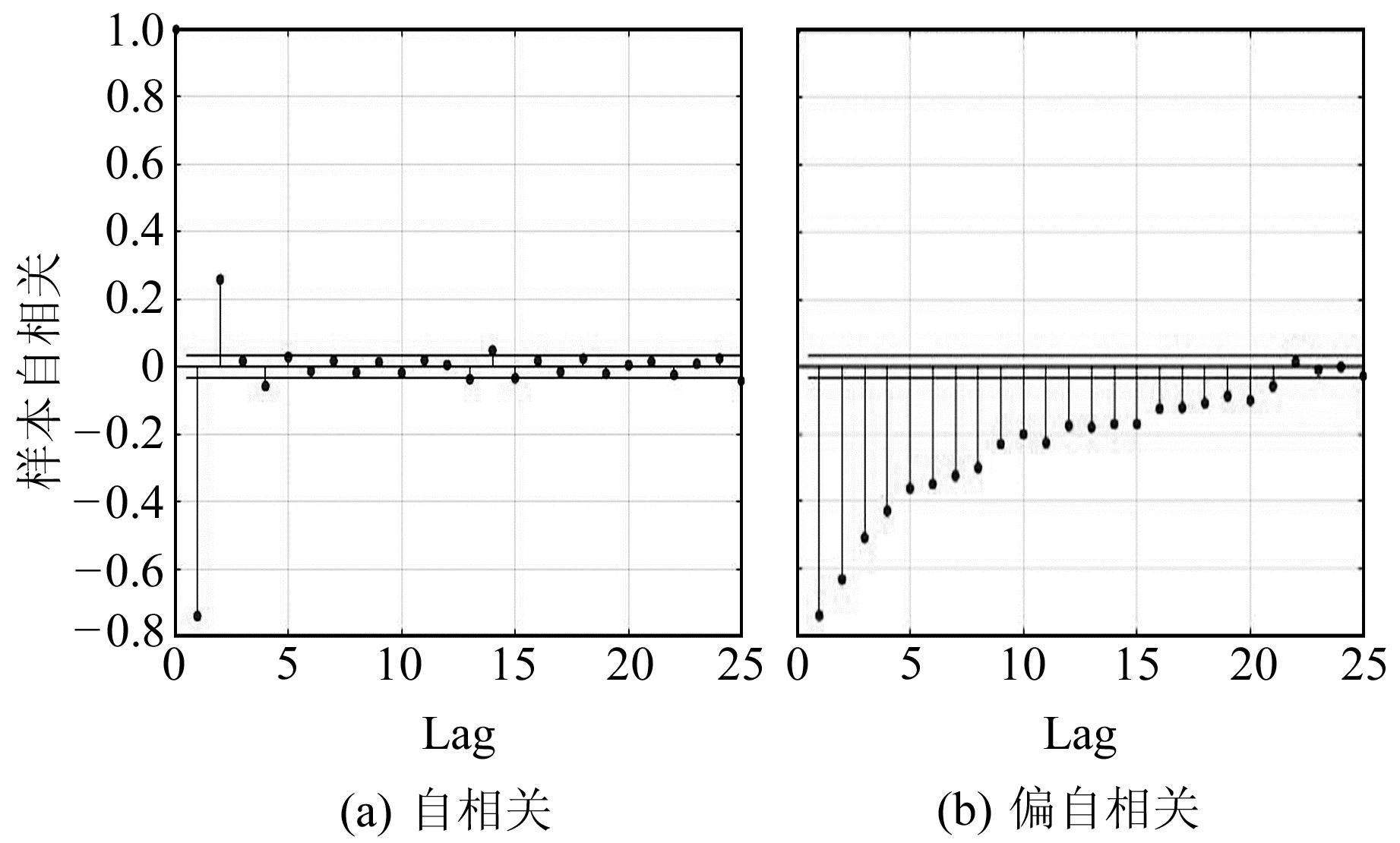
因为在时变分析时已经发现,NP.ang具有的周期项NP.ds同样具备,而且各小周期项幅值相对于火星周年项更大,加之NP.ds具有更高的精度,所以仅以NP.ds为例进行ARIMA模型的拟合。经过3次差分后发现,所得序列的ADF检验与KPSS检验结果已满足要求,因此,差分阶数d定为3。对二阶差分序列绘制自相关图与偏自相关图,根据图 3可以判断,p为21、q为4,因此选用的拟合模型应为ARIMA(21,3,4)。
|
图 3 自相关与偏自相关 Fig. 3 Since the correlation and partial autocorrelation diagrams |
此外,为了对比ARIMA模型与ARMA模型在非平稳时间序列拟合与预报上的差距,在进行ARIMA模型拟合与预报的同时也进行ARMA模型的拟合与预报。预报结束后,将二者的预报值分别与实际值作差,并绘制预报误差曲线,进而直观地对比二者在非平稳时间序列拟合与预报上的差距。
3.2 中长期预报模型 3.2.1 最小二乘外推模型最小二乘外推模型在研究地球极移长期预报问题的线性模型预报法中占有重要地位[10],本文选用的NP.ds时间序列的周期性要好于由IERS提供的地球极移参数结果,因此使用最小二乘外推模型对NP.ds时间序列进行拟合并进行中长期预报是可行的。在§2.2中已经确定了5个较为明显的周期项,因此本文最小二乘外推模型为:
| $ \begin{gathered} X(t)=a_0+a_1 t+\sum\limits_{i=1}^5 a_{2 i} \cos \left(2 \pi t / T_i\right)+ \\ \sum\limits_{i=1}^5 a_{2 i+1} \sin \left(2 \pi t / T_i\right) \end{gathered} $ | (9) |
式中,a0为常数项,a1为线性趋势项系数,a2~a11为周期项系数。
3.2.2 中长期预报中长期预报采用1991-01-02~2010-01-01星历数据,共计6 940 d。在确定用于拟合最小二乘外推模型的星历数据后,按照式(9)进行中长期预报。
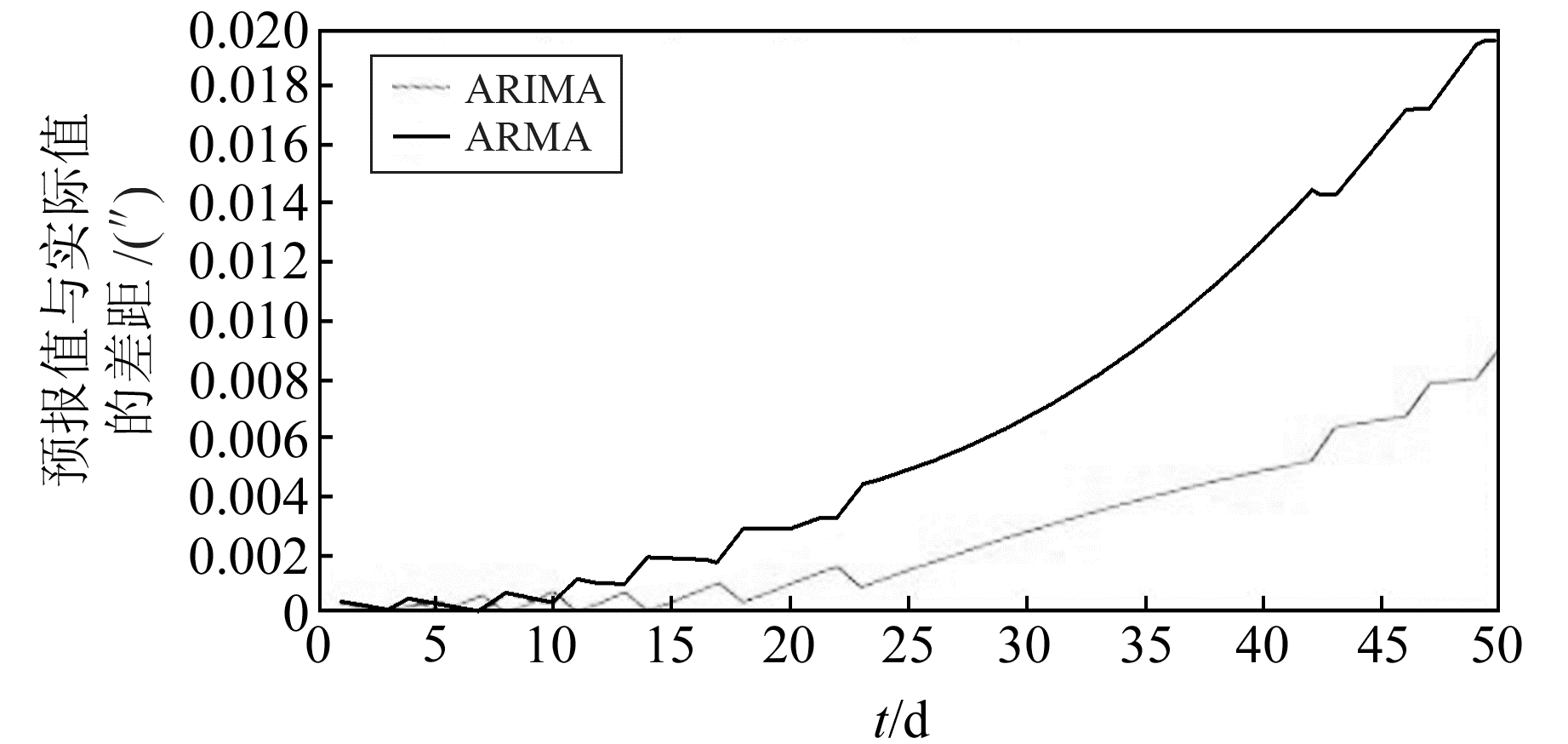
3.3 预报结果与分析 3.3.1 短期预报结果与分析对所选时间序列分别进行ARMA模型及ARIMA模型拟合,并对未来50 d的极移进行预报,ARIMA模型的预报值与实际值的偏差及ARMA模型的预报值与实际值的偏差如图 4所示。
|
图 4 ARIMA模型与ARMA模型预报误差 Fig. 4 ARIMA model and ARMA model forecast error |
由图 4可明显看出,前10 d两种模型预报误差的差异不太显著,但在第10 d后,ARIMA模型的预报效果显著优于ARMA模型,验证了ARIMA模型在处理非平稳时间序列时的优越性。
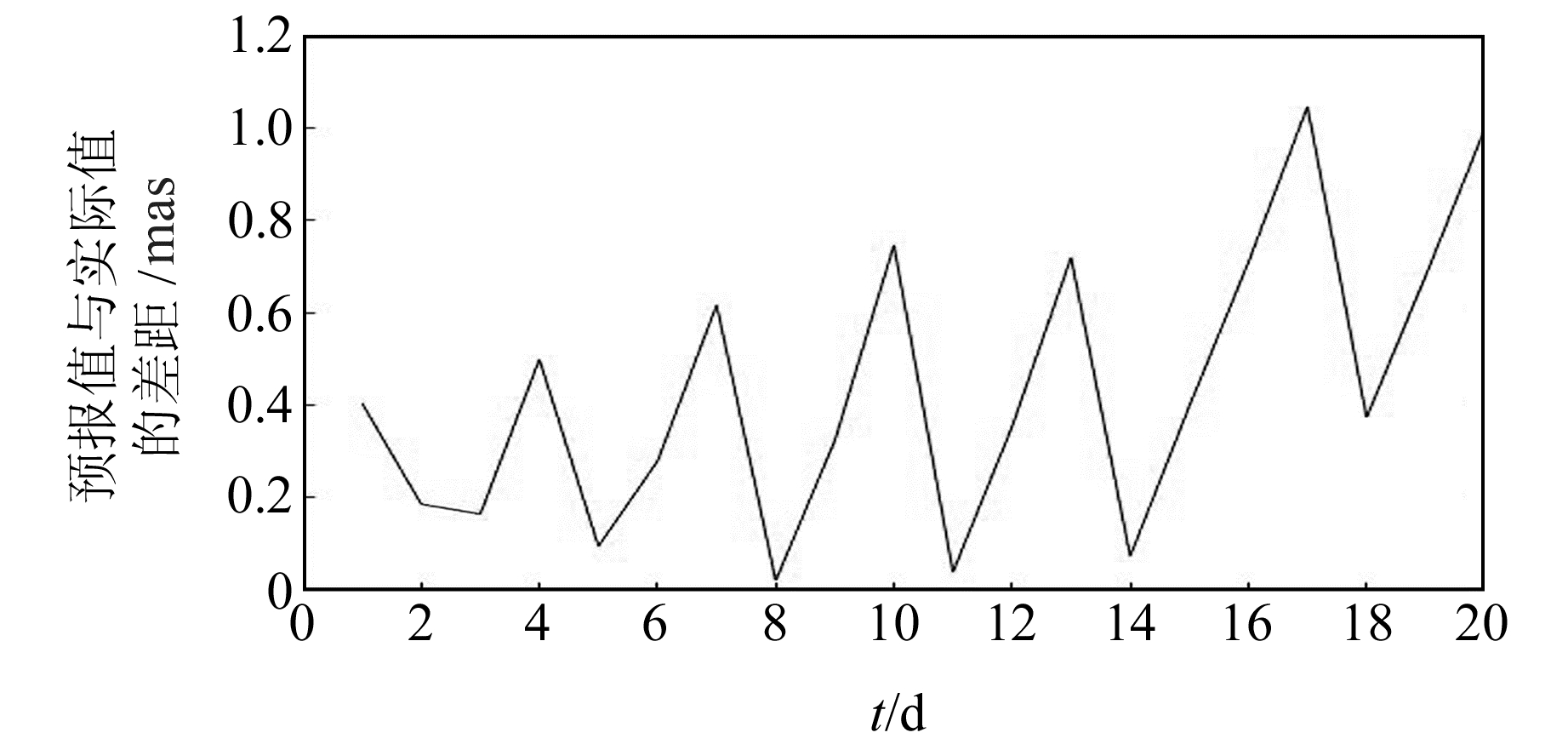
当把预报时间缩短至未来20 d时,ARIMA模型的预报值与实际值的偏差如图 5所示。由图可见,使用ARIMA模型对未来20 d的NP.ds数据进行预报,其误差基本在1.0 mas以内,小于星历数据本身的误差,这说明使用ARIMA模型对NP.ds进行20 d内的短期预报是可行的。
|
图 5 未来20 d的ARIMA模型预报误差 Fig. 5 Prediction error of ARIMA model in the next 20 days |
此外,通过观察图 4后半段的预报误差趋势发现,随着时间的推移,ARIMA模型的预报误差逐渐增大,尤其是第23 d后预报误差迅速增大,说明ARIMA模型不适合对NP.ds进行中长期预报。
3.3.2 中长期预报结果与分析对所选时间序列进行最小二乘外推模型(选用的周期项为§2.2中得到的5个周期项)拟合,并对未来5 a的极移进行预报,NP.ds中长期预报值与实际值的对比如图 6所示。由图 6(a)可见,预报值整体趋势与实际值基本一致,除了2个峰值差距较大外,2条曲线基本重合。事实上,即使是未来5 a中峰值的最大预报误差也在20 mas以内,这说明使用最小二乘外推模型进行NP.ds数据的中长期预报是可行的。

|
图 6 未来5 a中长期预报值与实际值对比及预报误差 Fig. 6 Comparison between medium-and long-term forecast values and actual values over the next 5 years, and forecast errors |
此外,通过进一步观察预报值与实际值差值的时间序列(图 6(b))可以发现,预报误差具有明显的周期性特征。
初步推测,这是由于最小二乘外推模型中采用的通过离散傅里叶变换获取的周期项结果与时间序列中蕴含的真正周期有一定差距,导致预报结果出现周期性误差。事实上,由离散傅里叶变换提取的周期项均应满足公式:
| $T=\frac{N}{k} $ | (10) |
式中,N为样本总数;k为频率,是0~(N-1)之间的整数。可以看出,在频率较小时,周期项之间周期长度的变化跨度较大,由离散傅里叶变换提取的长周期项结果与真实值的差距理论上要大于短周期项。换言之,就是短周期项的结果更接近时间序列中蕴含的真实周期。考虑到前文得到的各周期项与火星年具有很强的相关性,以其中最短的周期项(137.39 d)作为参考,得到一组新的用于拟合最小二乘外推模型的周期项(表 3)。
|
|
表 3 用于拟合最小二乘外推模型的周期项 Tab. 3 Period term used to fit Least squares extrapolation model |
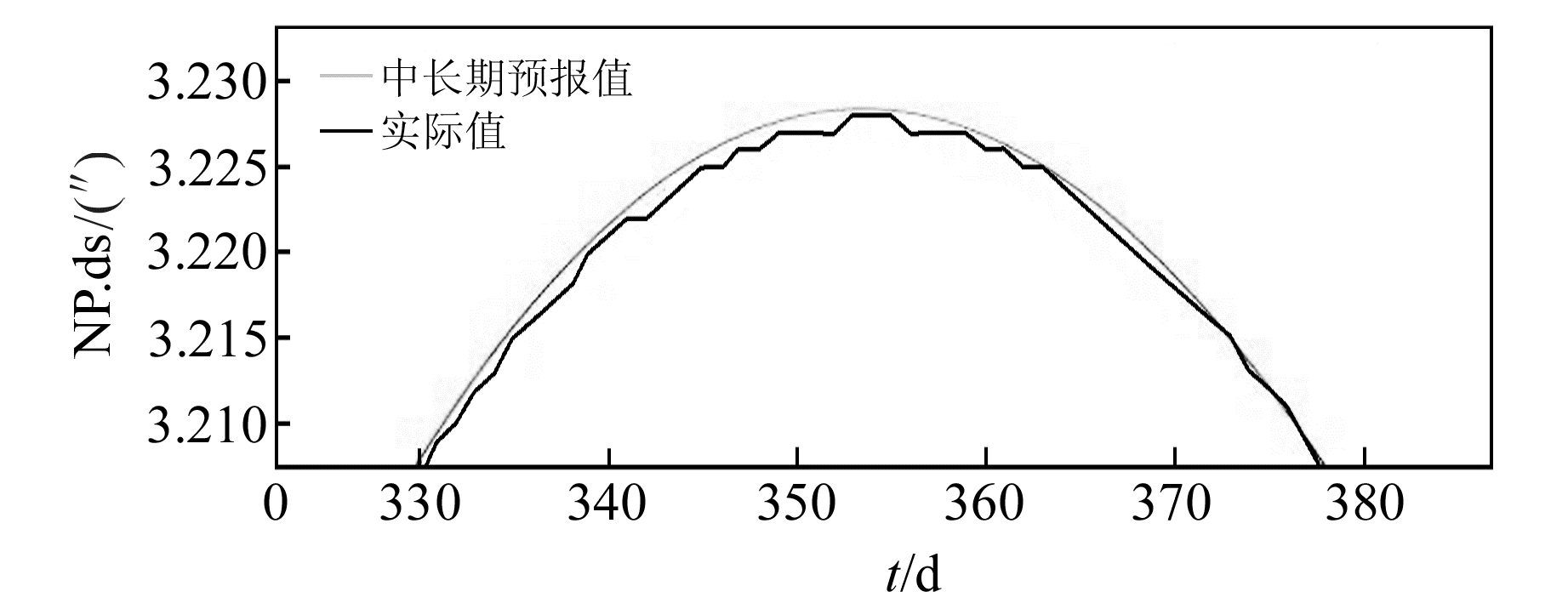
使用该组周期项进行拟合与预报,得到未来5 a的NP.ds中长期预报值与实际值对比图(图(7))。可以看出,2条曲线几乎完全重合,只有在峰值附近(图 8)才能发现预报结果仍有一定的误差。

|
图 7 未来5 a中长期预报值与实际值对比 Fig. 7 Comparison of medium-and long-term forecast values with actual values over the next 5 years |
|
图 8 中长期预报值与实际值在峰值附近的对比 Fig. 8 Comparison of mid-and long-term forecast values with actual values near the peak |
不过,这一结果仍验证了通过使用准确度更高的周期项进行最小二乘外推模型拟合,可显著提高对NP.ds中长期预报的精度,也进一步证明使用最小二乘外推模型对NP.ds进行中长期预报具有可行性。
4 结语本文利用NASA提供的NP.ang和NP.ds等包含火星极移信息的星历数据时间序列进行时变分析与预报,结果表明,NP.ang与NP.ds两组数据的周期项长度基本一致,且与火星年具有很强的相关性;短期预报的实验结果表明,使用ARIMA模型对NP.ds进行20 d内的短期预报是可行的;中长期预报实验结果表明,使用最小二乘外推模型进行NP.ds的中长期预报是可行的,且使用准确度更高的周期项进行最小二乘外推模型拟合,可显著提高对NP.ds中长期预报的精度。本文结果可为火星极移的预报研究提供参考。
| [1] |
Maistre S, Rosenblatt P, Rivoldini A, et al. Lander Radio Science Experiment with a Direct Link between Mars and the Earth[J]. Planetary and Space Science, 2012, 68(1): 105-122 DOI:10.1016/j.pss.2011.12.020
(  0) 0) |
| [2] |
Jacobson R A. Martian Satellite Orbits and Ephemerides[J]. Planetary and Space Science, 2014, 102: 35-44 DOI:10.1016/j.pss.2013.06.003
(  0) 0) |
| [3] |
Folkner W M, Williams J G, Boggs D H, et al. IPN Progress Report: The Planetary and Lunar Ephemerides DE430 and DE431[R]. California Institute of Technology, Pasadena, 2014
(  0) 0) |
| [4] |
Park R S, Folkner W M, Williams J G, et al. The JPL Planetary and Lunar Ephemerides DE440 and DE441[J]. The Astronomical Journal, 2021, 161(3): 105 DOI:10.3847/1538-3881/abd414
(  0) 0) |
| [5] |
Konopliv A S, Park R S, Rivoldini A, et al. Detection of the Chandler Wobble of Mars from Orbiting Spacecraft[J]. Geophysical Research Letters, 2020, 47(21)
(  0) 0) |
| [6] |
魏二虎, 李智强, 龚光裕, 等. 极移时间序列模型的拟合与预测[J]. 武汉大学学报: 信息科学版, 2013, 38(12): 1 420-1 424 (Wei Erhu, Li Zhiqiang, Gong Guangyu, et al. Fitting and Prediction of Pole Motion Time Series Model[J]. Geomatics and Information Science of Wuhan University, 2013, 38(12): 1 420-1 424)
(  0) 0) |
| [7] |
张林杰, 刘晖, 舒宝, 等. 极移时间序列建模及预测[J]. 测绘地理信息, 2021, 46(4): 40-43 (Zhang Linjie, Liu Hui, Shu Bao, et al. Modeling and Forecasting of Polar Motion Time Series[J]. Journal of Geomatics, 2021, 46(4): 40-43)
(  0) 0) |
| [8] |
于登云, 孙泽洲, 孟林智, 等. 火星探测发展历程与未来展望[J]. 深空探测学报, 2016, 3(2): 108-113 (Yu Dengyun, Sun Zezhou, Meng Linzhi, et al. The Development Process and Prospects for Mars Exploration[J]. Journal of Deep Space Exploration, 2016, 3(2): 108-113)
(  0) 0) |
| [9] |
林杨挺. 探索火星环境和生命[J]. 自然杂志, 2016, 38(1): 1-7 (Lin Yangting. Exploration of Paleoclimate and Possible Life on Mars[J]. Chinese Journal of Nature, 2016, 38(1): 1-7)
(  0) 0) |
| [10] |
高梧桐, 谢攀, 鄢建国. "火卫1"轨道预报与动力学分析[J]. 深空探测学报, 2019, 6(6): 570-579 (Gao Wutong, Xie Pan, Yan Jianguo. Orbit Prediction and Dynamical Analysis of Phobos[J]. Journal of Deep Space Exploration, 2019, 6(6): 570-579)
(  0) 0) |
2. School of Geography and Information Engineering, China University of Geosciences, 388 Lumo Road, Wuhan 430079, China;
3. GNSS Research Centre, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2023, Vol. 43
2023, Vol. 43


