2. 滁州学院地理信息与旅游学院,安徽省滁州市会峰西路1号,239000
甚长基线干涉测量(very long baseline interferometry, VLBI)对建立和维持国际地球参考框架(international terrestrial reference frame, ITRF)和国际天球参考框架(international celestial reference frame, ICRF),以及确定地球参考框架与天球参考框架之间相互转换所必需的地球自转参数(earth rotation parameters, ERP)具有重要作用[1]。地球自转参数包括2个部分:一是地球瞬时自转轴相对于地球表面或历元平极的运动,简称极移(polar motion, PM);二是地球自转变化,直接反映的观测量为日长(length of day)变化ΔLOD和世界时(universal time 1, UT1)与协调世界时(universal time coordinated, UTC)的差值(UT1-UTC)[2]。
由于台站和预算的局限性,目前VLBI网尚无法完全实现全球连续观测,因此国际大地测量和天体测量VLBI服务(international VLBI service for geodesy and astrometry, IVS)每周一(IVS-R1)和周四(IVS-R4)会组织约5~10个VLBI台站参与观测[3]。与此同时,为反映VLBI观测所能达到的最高精度,IVS每3 a会组织一次连续加密观测(continuous VLBI campaigns, CONT)[4]。为对比不同时段VLBI观测资料解算地球自转参数的差异,本文基于CONT08、CONT11、CONT14、CONT17观测资料和IVS-R1/R4定期观测的2008年、2011年、2014年、2017年观测数据进行地球自转参数序列解算并分析其精度差异性。同时,为比较不同技术解算地球自转参数精度的差异性,本文同时设计与CONT观测同时段的GPS观测资料参与地球自转参数解算实验。
1 实验原理 1.1 VLBI观测原理VLBI解算ERP的基本观测方程可表示为[5]:
| $ \tau(t)=-\frac{1}{C} \boldsymbol{b} \cdot s(t) $ | (1) |
式中,时间延迟τ为射电信号到达两台相距较远的射电望远镜的时间差;s为来自特定河外射电源的射电信号;b为两台射电望远镜之间的基线矢量; C为光速。
式(1)中b·s(t)在地球坐标系中可写为:
| $ \begin{gathered} \boldsymbol{b} \cdot s(t)=\cos \delta \cos (\alpha-\mathrm{GST}) \Delta X+ \\ \sin \delta \sin (\alpha-\mathrm{GST}) \Delta Y+\sin \delta \Delta Z \end{gathered} $ | (2) |
式中,ΔX、ΔY、ΔZ为基线矢量的分量,b为射电源在天球坐标系的坐标(赤经α和赤纬δ),GST为格林尼治恒星时。
根据式(1)和式(2)可得到时间延迟率:
| $ \begin{gathered} \dot{\tau}(t)=-\frac{\omega}{C}(\cos \delta \sin (\alpha-\mathrm{GST}) \Delta X- \\ \cos \delta \cos (\alpha-\mathrm{GST}) \Delta Y) \end{gathered} $ | (3) |
式中,地球自转速度ω为α-GST的时间导数。
在实际测量过程中,不可避免地存在一些误差源,因此实际观测方程为:
| $ \begin{gathered} \tau(t)=-\frac{1}{C} \boldsymbol{b} \cdot s(t)+\Delta \tau_{\text {Instr }}+ \\ \Delta \tau_{\text {ion }}+\Delta \tau_{\text {trop }}+\Delta \tau_{\text {clk }}+\cdots \end{gathered} $ | (4) |
基于上述原理,误差源通过加入仪器时延ΔτInstr、电离层时延Δτion、对流层时延Δτtrop、站间钟差Δτclk得到观测时间延迟。理论时间延迟通过加入先验台站、射电源坐标、地球形变、先验大地水准面参数和相对论效应等误差源而得到。通过计算观测时间延迟和修正后的理论延迟,得到最小二乘解。
1.2 精度评定为评定地球自转参数的解算精度,本文利用均方根误差(RMSE)作为外符合精度:
| $ \operatorname{RMSE}=\sqrt{\frac{\sum\limits_{i=1}^n\left(\tilde{x}_i-x_i\right)^2}{n}} $ | (5) |
式中,n为地球自转参数序列的个数,
VLBI观测包括各种系列的24 h观测计划,该计划由观测计划委员会制定,由IVS协调中心协调,并由网络站、操作中心和相关人员执行,通常情况下,每周只有2~4次定期的24 h VLBI观测[6]。为获取连续的高频地球自转参数序列以及当前VLBI最优观测数据资料,国际目前已经组织多次CONT观测,本文基于CONT08、CONT11、CONT14、CONT17观测资料进行地球自转参数解算,表 1为参与CONT观测的测站信息。
|
|
表 1 参与CONT观测的台站信息 Tab. 1 Information of stations participating in CONT campaigns |
本文实验数据来源于IVS(https://cddis.nasa.gov/),观测资料为CONT观测数据以及对应的IVS组织每周一和周四定期观测的IVS-R1和IVS-R4年观测数据,数据格式为NGS。解算数据序列分别为CONT08、CONT11、CONT14、CONT17、IVS-R1/R4(2008)、IVS-R1/R4(2011)、IVS-R1/R4(2014)、IVS-R1/R4(2017)。解算策略为:地球参考框架选择ITRF2014,天球参考框架为ICRF3,星历为JPL421,对流层映射函数为VMF3,电离层延迟从观测资料中读取,海洋潮汐模型选择FES2004,岁差章动模型选择IAU2006/2000A,台站改正还需考虑固体潮、极潮、潮汐大气负荷、非潮汐大气负荷、天气热变形等因素。由于VLBI观测不连续,故采用三次样条插值缺失的地球自转参数时间序列。
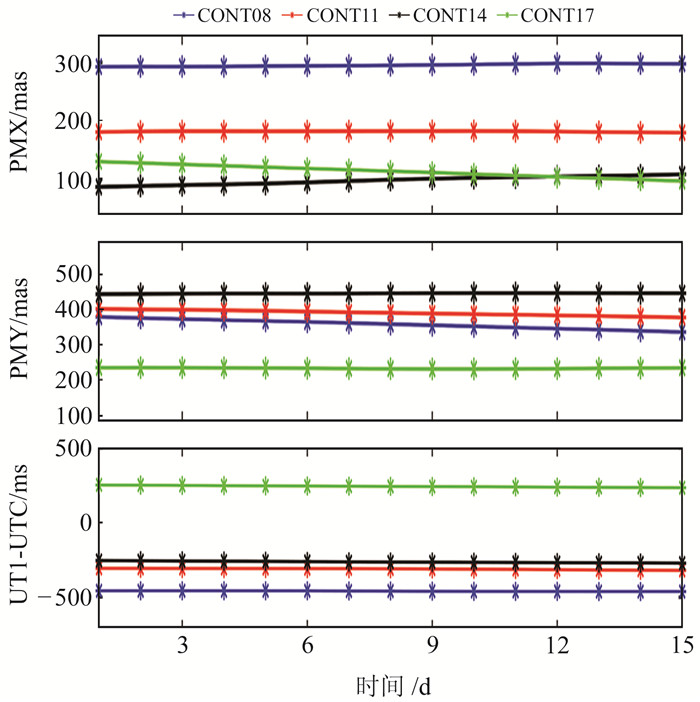
3.1.2 实验结果分析本文基于维也纳理工大学提供的维也纳VLBI与卫星软件(Vienna VLBI and satellite software, VieVS)进行地球自转参数解算[7],图 1为VieVS软件解算CONT观测值的地球自转参数序列。
|
图 1 基于CONT观测值的ERP天解 Fig. 1 ERP with daily resolution estimated from CONT campaigns |
从图 1可以看出,CONT观测值解算后的地球自转参数序列图像平滑,未出现明显的系统误差,并且利用CONT17观测值解算的地球自转参数序列较小,极移序列在100~200 mas左右波动,UT1-UTC在200~250 mas左右波动。与其他CONT观测数据相比,该观测资料解算精度更高的原因为:CONT17具有更多的台站参与观测,并且这些台站位于更优的几何位置来估算地球自转参数,如部分台站位于经度0°或180°南北方向,解算时具有更长的基线解。
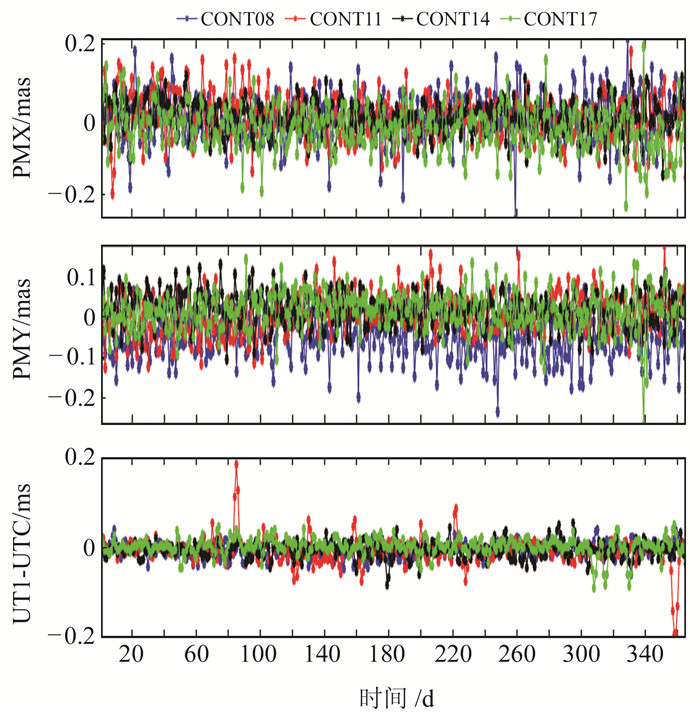
为对比IVS每周一和周四定期观测的IVS-R1和IVS-R4观测数据和CONT观测数据精度的差异性,本文同时设计基于IVS-R1/R4年观测数据解算地球自转参数序列。由于IVS-R1/R4观测数据不连续,所选时段内的地球自转参数序列缺失值较多,因此本文利用三次样条插值法对缺失值进行估算。图 2为基于IVS-R1/R4观测值解算后的地球自转参数序列与IERS提供的EOP14 C04序列对比值。
|
图 2 基于IVS-R1/R4观测值与EOP14 C04作差后的ERP年解 Fig. 2 Residual ERP with yearly resolution between IVS-R1/R4 observations and EOP14 C04 series |
从图 2可以看出,基于IVS-R1/R4年观测值解算后的地球自转参数与IERS提供的地球自转参数序列吻合较好,说明IVS-R1/R4观测值无系统偏差,但部分参数解算时出现离散值,主要表现在2008年观测时期,IVS-R1/R4在解算极移序列时出现部分离散值,原因为该时期出现较强的未知激发因素或理论模型本身存在一定缺陷。
从表 2可以看出,对比其他CONT观测值解算精度,CONT17观测值的极移解算精度有显著提升,极移在X方向上的RMSE提升约41%,在Y方向上的RMSE提升约43%,主要原因为:一是参与台站的数目更多,二是观测的季节也是影响精度的因素。如对比CONT08观测时期,CONT17主要集中在冬季进行观测,此时可能激发源较少[8]。
|
|
表 2 不同观测值解算结果的精度统计 Tab. 2 Accuracy statistics of the solved results from different observations |
对比IVS-R1/R4定期观测的VLBI年观测资料地球自转参数的解算精度发现,CONT观测值的解算精度具有更突出的优势,其极移精度提升约30%, UT1-UTC精度提升约45%。主要是由于IVS-R1/R4观测仅有5~10个台站参与并且其数据记录速率仅为256 Mbit/s,而CONT观测值数据记录速率多为512 Mbit/s。其次,VLBI观测时间的连续性对解算精度具有一定影响。
3.2 利用GPS观测资料解算地球自转参数为进一步对比不同技术解算地球自转参数精度的差异性,本文同时设计GPS观测资料参与地球自转参数序列解算,其中解算时间段与CONT观测值同期,解算软件为GAMIT/GLOBK 10.61,解算策略与VieVS软件保持一致。选取86个全球分布均匀、站址稳定的IGS测站参与地球自转参数序列解算。由于GPS观测资料解算地球自转参数序列无法直接获取UT1-UTC,故本文采用LOD代替UT1-UTC精度。
图 3为GPS观测值解算地球自转参数的天解,可以看出,GPS观测值解算地球自转参数序列图像整体也呈现平滑状态,无系统误差,原因主要为解算时间段内选择的GPS台站充足且在全球分布均匀。

|
图 3 基于GPS观测值的ERP天解 Fig. 3 ERP with daily resolution estimated from GPS observations |
表 3为GPS观测值解算结果精度统计,对比VLBI同时期的地球自转参数解算精度(表 2)发现,GPS的极移序列解算精度高于VLBI观测资料,这主要是因为GPS观测技术在该时段内保持观测时间连续、数据量充足、测站稳定且分布均匀。而LOD解算精度低于VLBI,原因为VLBI台站本身观测精度高于GPS台站。
|
|
表 3 GPS观测值解算结果精度统计 Tab. 3 Accuracy statistics of the solved results from GPS observations |
本文采用不同类型观测值和不同技术间观测值参与地球自转参数解算,讨论不同类型观测值和不同技术间观测值对地球自转参数解算精度的差异性,分析精度差异性原因,主要得到以下结论:
1) 不同时期的CONT观测值解算地球自转参数精度差异较大,主要原因为观测台站数目不同,其次是不同观测时期的激发源可能不同,该部分有待进一步研究。
2) 对比IVS-R1/R4年观测资料,CONT观测值解算地球自转参数序列的精度更优,其极移精度提升约30%,UT1-UTC精度提升约45%,主要原因为参与CONT观测的台站更多并且数据记录速率更快,其次CONT观测时段更为连续,VLBI数据记录丢失率更低。
3) 对比不同技术间解算地球自转参数精度的差异性可知,GPS观测资料解算的极移精度具有更突出的优势,原因为GPS观测资料在该时段内保持观测时间连续、数据量充足、测站稳定且分布均匀。而VLBI解算UT1-UTC的精度更具优势,主要原因为VLBI观测台站本身精度较GPS台站的高。
| [1] |
魏二虎, 刘文杰, Wei Jianan, 等. VLBI和GPS观测联合解算地球自转参数和日长变化[J]. 武汉大学学报: 信息科学版, 2016, 41(1): 66-71 (Wei Erhu, Liu Wenjie, Wei Jianan, et al. Estimation of Earth Rotation Parameters and ΔLOD with Combining VLBI and GPS Observations[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 66-71)
(  0) 0) |
| [2] |
Kalarus M, Schuh H, Kosek W, et al. Achievements of the Earth Orientation Parameters Prediction Comparison Campaign[J]. Journal of Geodesy, 2010, 84(10): 587-596 DOI:10.1007/s00190-010-0387-1
(  0) 0) |
| [3] |
Schuh H, Behrend D. VLBI: A Fascinating Technique for Geodesy and Astrometry[J]. Journal of Geodynamics, 2012, 61: 68-80 DOI:10.1016/j.jog.2012.07.007
(  0) 0) |
| [4] |
Nilsson T, Heinkelmann R, Karbon M, et al. Earth Orientation Parameters Estimated from VLBI during the CONT11 Campaign[J]. Journal of Geodesy, 2014, 88(5): 491-502 DOI:10.1007/s00190-014-0700-5
(  0) 0) |
| [5] |
James C. Very Long Baseline Interferometry: A High Precision Tool for Geodesy and Astrometry[J]. Comptes Rendus De Lacadémie Des Sciences, 2000, 1(10): 1 255-1 265
(  0) 0) |
| [6] |
Behrend D, Thomas C, Gipson J, et al. On the Organization of CONT17[J]. Journal of Geodesy, 2020, 94(10): 1-13
(  0) 0) |
| [7] |
Böhm J, Böhm S, Boisits J, et al. Vienna VLBI and Satellite Software(VieVS) for Geodesy and Astrometry[J]. Publications of the Astronomical Society of the Pacific, 2018, 130(986)
(  0) 0) |
| [8] |
谢伯全, 郑大伟. 大气对地球自转参数(ERP)的高频激发[J]. 天文学报, 1996, 37(2): 113-123 (Xie Boquan, Zheng Dawei. High Frequency Excitation of Earth Rotation Parameters(ERP) from Atmosphere[J]. Acta Astronomica Sinica, 1996, 37(2): 113-123)
(  0) 0) |
2. School of GeographicInformation and Tourism, Chuzhou University, 1 West-Huifeng Road, Chuzhou 239000, China
 2023, Vol. 43
2023, Vol. 43


