定点地形变观测具有精度高、频带宽和连续性好等优点,是研究构造运动、断层滑移和地震前兆等诸多动力学问题的重要手段之一[1]。目前,一般采用SS-Y型伸缩仪进行定点台站洞体应变固体潮观测,获得的线应变固体潮观测资料可进行潮汐主应变、主方向和剪应变计算[2-3],以分析观测场地的平面应变状态及区域应变场变化和地震前兆异常。就地震前兆研究而言,全面、深入地分析震前形变异常特征及其成因机制,对地震分析预测不仅重要也极具必要性。
金寨台位于华北地块、下扬子地块与秦岭-大别断褶带的交汇处,附近有多条断裂带经过,区域构造较为复杂。台站SS-Y伸缩仪EW分量2020-05-07开始趋势陡转,出现大幅持续下降形态的压性异常变化,至08-06(共计92 d)下降幅度达12 784×10-10。虽然对台站观测系统和周边环境进行了多次调查,但至今仍未厘清该异常的性质及成因机制。本文根据金寨台区域水文、构造特征及地震活动性等,基于观测环境,拟从气象因素(气温、气压、降雨、洞温)变化、附近水体(水库、河流)载荷情况及区域地壳应力场变化等可能的成因机制角度,探讨此次异常的最佳成因,以期为该区域地震前兆研究提供助益。
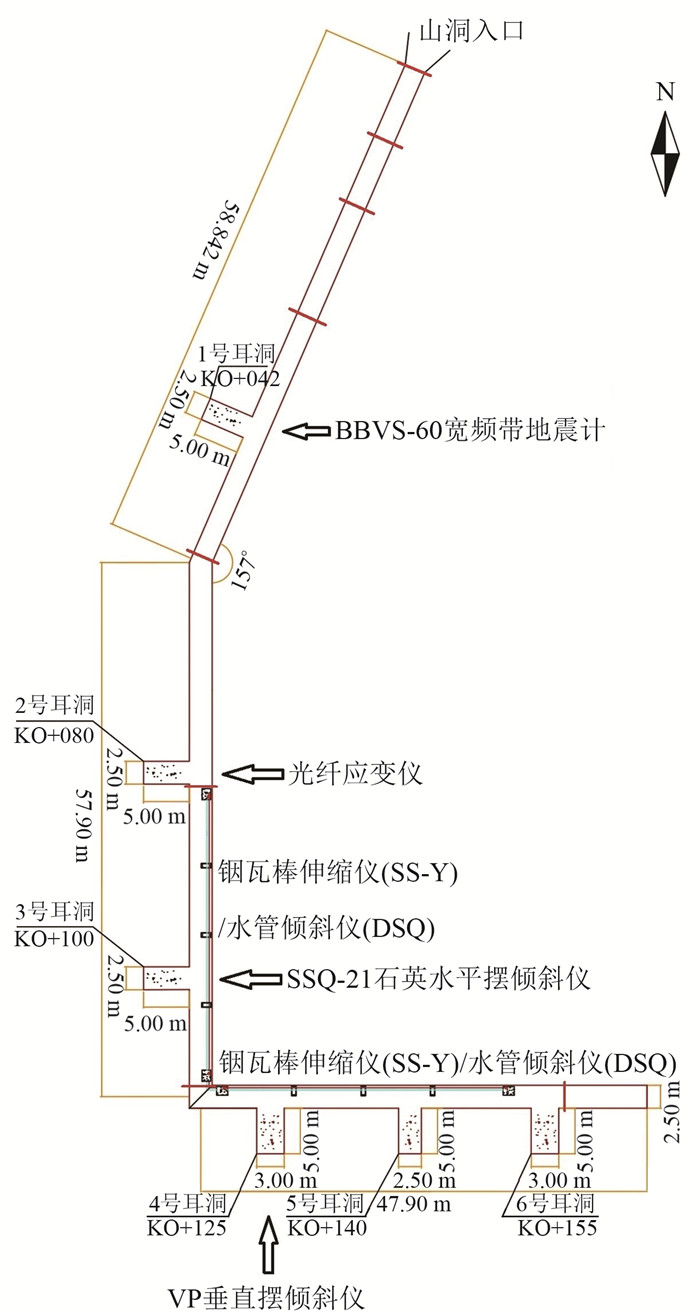
1 台站概况及区域构造背景金寨台形变观测山洞全长164.642 m,引洞(近NS向)长58.842 m,主洞正NS向长57.900 m、正EW向长47.900 m,主要有地倾斜和洞体应变2种观测项目,其中洞体应变观测仪器SS-Y型伸缩仪放置在主洞2个方向上(图 1)。
|
图 1 金寨台山洞形变仪器布置分布 Fig. 1 Layout and distribution of cave deformation instruments at Jinzhai station |
金寨台洞体应变测量原理是测量地表面两点间基线长度的相对变化量,即
| $ \varepsilon=\frac{L^{\prime}-L}{L}=\frac{\Delta L}{L} $ | (1) |
式中,L为原地壳表面两点间的距离,称为基线长;L′为变化后地壳表面两点间的距离;ΔL为基线的绝对变化量;ε为应变量,即单位长度的相对变化量。根据约定,压缩为负、拉张为正,即ε<0时L压缩、ε>0时L拉张。
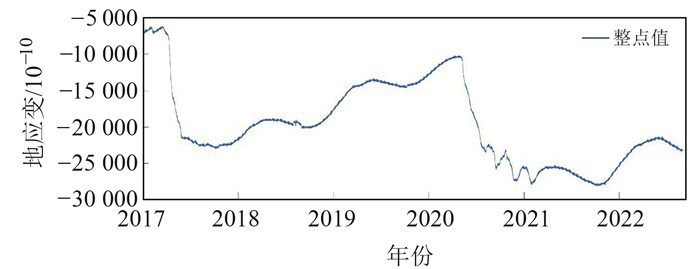
2 EW分量压性异常特征判断金寨洞体应变自2016-11开始观测以来EW分量除了出现过2次大幅下降的压性异常变化外,其他时段年变规律、趋势变化相对稳定(图 2)。第1次压性异常变化为2017-04-10~05-28(共计49 d),EW分量变化幅度13 731×10-10,经核实认定为自然环境和场地环境干扰综合事件,因降雨、水库水位涨落、水库泄洪、史河水位上涨等因素综合影响引起的快速变化;第2次压性异常变化自2020-05-07开始,EW分量趋势陡转,出现大幅持续下降,至08-06(共计92 d)EW分量数据下降幅度达12 784×10-10;08-07开始EW分量在保持缓慢下降的趋势背景下出现3次张性鼓包现象,2021-01底异常结束,数据曲线转入正常年变形态。2次变化均为快速下降压性变化,2017年的下降变化结束后立即恢复正常年变,2020-08-06下降变化结束后并未回归正常年变,而是出现了“三上三下”的应变调整形态(图 2),并于2021-01底回归正常年变。
|
图 2 金寨台洞体应变EW分量观测整点值曲线 Fig. 2 Point value curve of EW component observation of tunnel body strain at Jinzhai station |
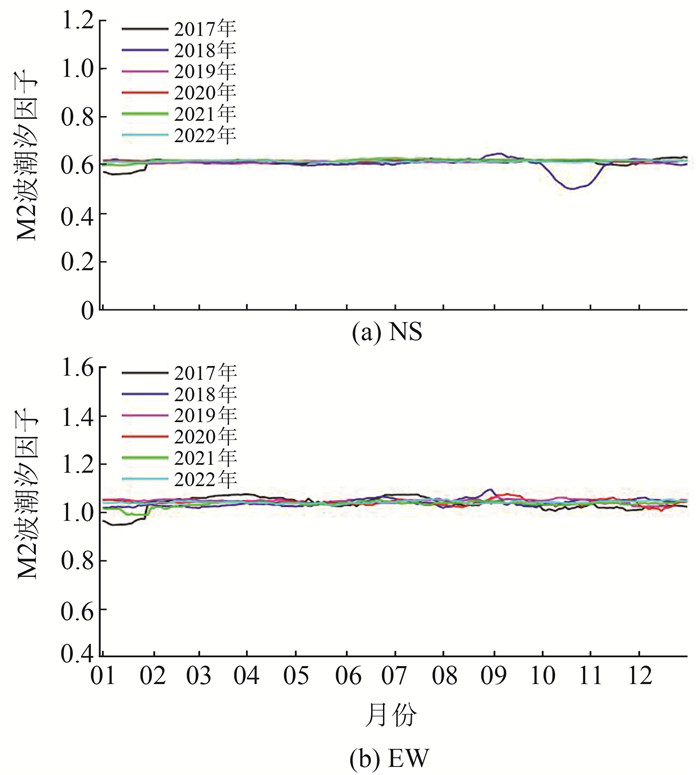
2次压性异常变化期间,观测系统运行正常,无检修仪器等人为干扰情况。为进一步分析金寨洞体应变EW分量大幅压性异常变化期间数据的可靠性,计算2017~2022年洞体应变NS分量和EW分量M2波潮汐因子,结果见图 3。结果表明,NS分量和EW分量的M2波潮汐因子相对稳定。NS分量在2018-09~10因多次检修更换传感器,导致潮汐因子变化较大,其他时间潮汐因子均在0.616左右;EW分量潮汐因子比NS分量潮汐因子大,但均在1.042左右。除受到仪器检修影响外,2个分量潮汐因子相对稳定,故认为仪器观测数据质量可靠,压性异常排除观测系统存在问题的可能性。对比金寨台其他形变观测项目及周边泾县台、淮北台、泗县台、麻城台洞体应变同时段观测数据,均未发现类似压性异常变化。
|
图 3 金寨台洞体应变NS、EW分量M2波潮汐因子 Fig. 3 Tidal factor of M2 wave of NS, EW components of tunnel volume strain at Jinzhai station |
综上可知,在排除观测系统故障及人为干扰等因素后,金寨台2020年EW分量的压性下降变化与2017年的压性下降变化在形态上存在相似性和差异性,亟需从其他角度分析判断变化原因。本文拟从气象因素影响、周边场地环境变化、区域地壳应力场变动等方面分析此次压性下降变化的原因。
3 EW分量压性异常3种可能的成因机制 3.1 气象因素触发机制分析金寨台除了地倾斜和洞体应变观测外,还配有气象三要素辅助观测,收集历年来的气象观测资料及洞温观测资料。本文收集整理洞体应变观测以来气温、气压、洞温、降雨量、实测应变等变化量,建立回归分析模型,得到2020年压性下降变化期间因气温、气压、洞温及降雨量变化引起的理论应变变化量,并与金寨台同时段实测洞体应变变化量进行对比分析。
首先,针对各气象因素与应变变化之间进行一元线性回归分析,由于本文收集到的气象因素变化导致的洞体应变变化量与2020年洞体应变EW向压性下降变化量相差较大,作图时存在压制现象,因此对所有气象因素变化量、洞体应变变化量作对数处理,再进行一元线性回归分析。如图 4所示,气温及气压均与洞体应变存在明显的线性关系,但2020-05-07~08-06实际观测应变变化量(图 4中红色圆圈)与一元线性回归拟合曲线相差较远;降雨量及洞温均与洞体应变无明显线性关系。

|
图 4 应变变化回归分析 Fig. 4 Regression analysis of strain change |
其次,运用气温、气压、降雨量及洞温与洞体应变建立多元线性回归模型,表达式为:
| $ \begin{gathered} y=9.522+1.512 x_1+15.705 x_2+ \\ 0.182 x_3+50.926 x_4 \end{gathered} $ | (2) |
式中,y为洞体应变变化量,x1为气温变化量,x2为气压变化量,x3为降雨量,x4为洞温变化量。如图 5所示,多元线性回归拟合曲线与洞体应变变化曲线相差较大,拟合优度为0.543,表明洞体应变变化的54.3%可由模型确定;误差方差为89.615,模型误差较大。将2020-05-07~08-06气温、气压、降雨量、洞温变化值代入式(2),得到模型理论应变变化量为394×10-10,与同时段EW分量应变变化幅度12 784×10-10相差较大。

|
图 5 气温、气压、降雨、洞温与洞体应变多元线性回归分析 Fig. 5 Multiple linear regression analysis of air temperature, air pressure, rainfall, cave temperature and cave body strain |
综上可知,平常情况下,金寨台洞体应变EW分量在气温、气压与应变之间存在线性影响。针对2020-05-07~08-06洞体应变EW分量压性下降变化,无论是气温、气压的一元线性回归拟合结果,还是气温、气压、降雨量及洞温的多元线性回归拟合结果,均与实际观测应变变化量相差较大,说明此次大幅压性下降变化不是气象因素所致。
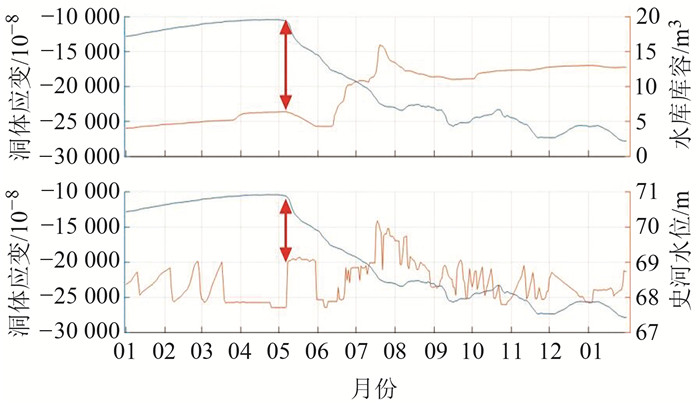
3.2 水体载荷变化分析梅山水库位于金寨台西南方向约2 km,总库容23.370亿m3,常年蓄水约10亿m3。史河从梅山水库发源,从台站西北方向流过,最近距离约500 m。收集梅山水库和史河的相关水文数据可以发现,2020-05-07金寨台洞体应变EW分量发生压性下降时,梅山水库开始泄洪、下游史河水位陡升,时间上存在较强的相关性(图 6)。
|
图 6 梅山水库库容变化、史河水位变化与洞体应变EW分量对比 Fig. 6 Comparison of EW components of reservoir capacity change, Shihe river water level change and tunnel body strain in Meishan reservoir |
建立三维不规则形状载荷模型[4]推算压性下降变化时段内水库库容变化及史河水位变化造成的应变变化量。针对三维不规则形状载荷模型,可将该模型的总作用力F进行网格化,分别求取各网格内作用力f对台站观测点造成的垂向和水平NS、EW向位移,然后求所有网格块对观测点作用的矢量和,即可得到观测点垂向和水平NS、EW向位移。各网格内作用力f对台站观测点造成的水平EW、NS向位移为[5]:
| $ u=\frac{f x z}{4 {\rm{ \mathsf{ π} }} G R^3}-\frac{f x}{4 {\rm{ \mathsf{ π} }}(G+\lambda) R(R+z)} $ | (3) |
| $ v=\frac{f y z}{4 {\rm{ \mathsf{ π} }} G R^3}-\frac{f y}{4 {\rm{ \mathsf{ π} }}(G+\lambda) R(R+z)} $ | (4) |
式中,u为x轴(即水平EW向)位移;v为y轴(即水平NS向)位移;f为各网格内载荷作用力;
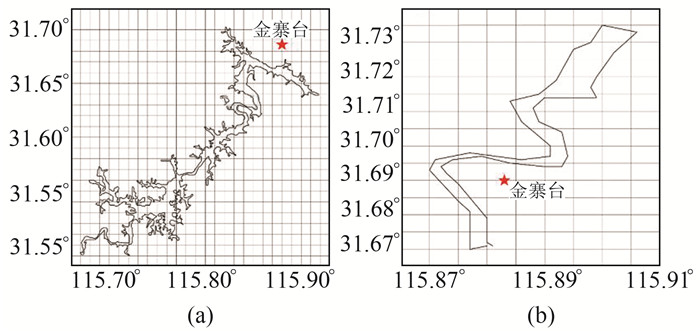
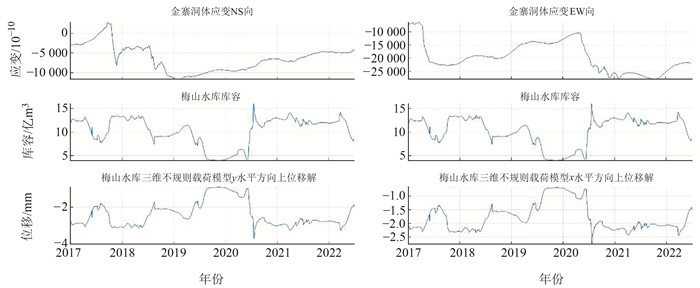
首先建立梅山水库的三维不规则形状载荷模型,将其简略划分为58个截面为1 000 m×1 000 m的网格块,如图 7(a)所示,运用式(3)和式(4)分别计算不同水库库容时这58个网格块对洞体应变观测点造成的位移矢量和,结果如图 8所示。根据模型计算结果,2020-05-07~08-06金寨台洞体应变EW分量受水库载荷变化引起的理论位移变化量为-2.030 mm。金寨台洞体应变仪EW分量基线长L=28.28 m,2020-05-07~08-06观测值总变化量为-12 784×10-10,运用式(1)可换算得到台站洞体应变观测基线的绝对变化量ΔL为-0.036 mm,与数值模拟的同时段理论位移变化量-2.030 mm相差2个数量级,说明2020年金寨台洞体应变压性异常变化与同时期梅山水库载荷变化的相关性较小。
|
图 7 梅山水库、史河不规则形状载荷网格化示意图 Fig. 7 Meshing diagram of irregular shape load of Meishan reservoir and Shihe river |
|
图 8 梅山水库三维不规则载荷模型水平方向位移解 Fig. 8 Horizontal displacement solution of 3D irregular load model of Meishan reservoir |
其次,建立史河的三维不规则形状载荷模型,将其简略划分为14个截面为500 m×500 m的网格块,如图 7(b)所示,运用式(2)和式(3)分别计算史河不同水位时14个网格块对洞体应变观测点造成的位移矢量和,结果如图 9所示。根据模型计算结果,2020-05-07~08-06金寨台洞体应变EW分量受史河水位变化(水位最大变幅为2.46 m)引起的理论位移变化量为-0.023 mm,与洞体应变实测位移变化量-0.036 mm相差不大,考虑与三维不规则载荷模型的地形近似、网格近似划分、未考虑沉积层影响等近似条件的设置有关,因此认为2020年压性下降的前期快速下降变化与史河水位变化有较大相关性。

|
图 9 史河三维不规则载荷模型水平方向位移解 Fig. 9 Horizontal displacement solution of 3D irregular load model of Shihe river |
结合图 8和图 9还可以看出,无论是水库库容变化还是史河水位变化,模型中NS分量位移量均大于EW分量,说明梅山水库库容变化或史河水位变化对金寨台周边区域位移的影响NS向大于EW向。
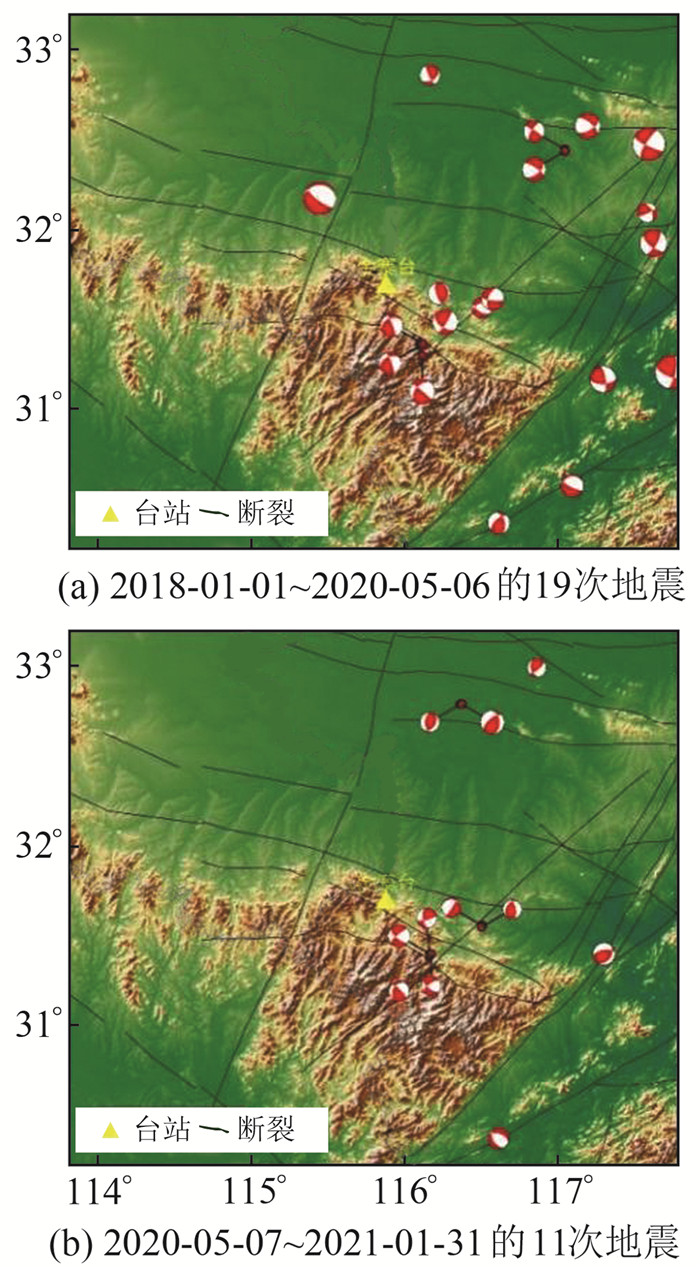
3.3 区域地壳应力场变动分析为进一步分析2020年压性异常变化时段金寨台所在区域(30.2°~33.2°N,113.8°~117.8°E)地壳应力场的变化情况,采用Snoke方法对正常时段(2018-01-01~2020-05-06)和洞体应变压性下降异常时段(2020-05-07~2021-01-31)研究区ML≥2.3地震的震源机制解进行解算,共得到30个较可靠的震源机制解,结果如图 10所示。之后,利用力轴张量法进行反演,获取该区域地壳应力场的时空变化特征(图 11)。
|
图 10 压性异常前后研究区域内30次ML≥2.3地震的震源机制解 Fig. 10 Focal mechanism solutions of 30 ML≥2.3 earthquakes in the studied area before and after the compressive anomaly |
|
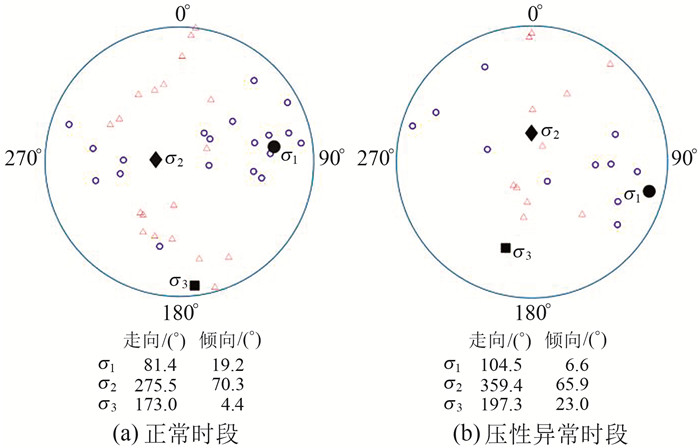
空心圆、空心三角形分别代表P轴、T轴,实心圆、实心菱形和实心正方形分别代表主压应力σ1、中间应力σ2、主张应力σ3 图 11 震源机制解P、T轴和主应力轴σ1、σ2、σ3在下半球吴尔夫网上的投影 Fig. 11 P-axis, T-axis, and principal stress axis of focal mechanism solution σ1, σ2, σ3 projection on the Wolff network in the lower hemisphere |
结果显示,正常时段该区域主压应力σ1的方位角为81.4°、倾角为19.2°,呈NEE向、低倾角;主张应力σ3的方位角为173°、倾角为4.4°,呈SSE向、近水平,表明正常时段该区域处于近EW向低倾角压应力和近NS向近水平张应力的区域构造应力作用。
而2020年压性异常时段,该区域主压应力σ1的方位角为104.5°、倾角为6.6°,呈SEE向、应力轴接近水平;主张应力σ3的方位角为197.3°、倾角为23°,呈SSW向、低倾角,可见虽然也处于近EW向压应力和近NS向张应力的区域构造应力作用中,但相较于正常时段而言,主压应力方位角发生顺时针偏转,偏转幅度约24°。
倪红玉等[6]利用阻尼区域应力反演方法研究表明,安徽地区受近EW向水平挤压和近NS向水平拉张的现代构造应力场作用,最大主压应力方向在空间上从北到南也存在一定程度的偏转。金寨台洞体应变EW分量压性异常发生前后,研究区主压应力轴σ1和主张应力轴σ3的方位角总体趋势较为一致,存在一定程度的顺时针偏转,这与倪红玉等[6]的研究结果一致。由此说明,金寨台洞体应变EW分量压性异常发生前后该区域构造应力场未发生显著变动,2020年金寨台洞体应变压性异常变化由区域构造应力场变化引起的可能性较小。
4 结语针对金寨台洞体应变EW分量在2020年出现的压性下降异常,在排除观测系统故障、人为干扰等因素后,提出并分析了3种可能的成因机制,得到以下初步认识:
1) 通过气温、气压、降雨、洞温的一元或多元线性回归分析发现,气温变化、气压变化与应变变化之间虽然存在线性影响,但拟合结果与实际观测应变变化量相差较大,说明此次大幅压性下降变化不是气象因素所致。
2) 2020-05-07金寨台洞体应变EW分量发生压性下降时,梅山水库开始泄洪、下游史河水位陡升,时间上存在较强的相关性;三维不规则载荷模型数值模拟结果显示,洞体应变压性的前期快速下降变化与同时期梅山水库载荷变化的相关性较小,与史河水位变化有较大相关性,说明此次大幅压性下降变化由梅山水库泄洪触发,之后受下游史河蓄水量较大影响所致。
3) 洞体应变EW分量压性异常发生前后,研究区主压应力轴σ1和主张应力轴σ3的方位角总体趋势较为一致,进一步说明异常前后该区域构造应力场未发生显著变动,因此洞体应变压性异常变化由区域构造应力场变化引起的可能性较小。初步推定,金寨台洞体应变EW分量压性下降异常很可能是受周边场地环境载荷变化的影响所致。
受水文资料限制,本文对地形变化、地下介质分布、物性参数、相关模型参数等进行了简化和近似,数值模拟得到的结果与实际位移变化量在数量级上基本一致,可为今后定点形变出现大幅变化后的判定提供定性与定量分析的思路。下一步考虑结合同台其他定点形变观测资料作进一步对比分析,为该区域震情跟踪提供助益。
| [1] |
杨小林, 王军, 王希彬, 等. 陕西韩城台巨幅地倾斜异常的成因分析[J]. 地震学报, 2018, 40(6): 760-773 (Yang Xiaolin, Wang Jun, Wang Xibin, et al. What Causes the Remarkable Tilt Anomalies at the Hancheng Geodynamic Observatory in Shaanxi Province?[J]. Acta Seismologica Sinica, 2018, 40(6): 760-773)
(  0) 0) |
| [2] |
刘序俨, 李平, 张雁滨. 地表的面应变和体应变固体潮理论值计算及其调和分析[J]. 地壳形变与地震, 1988, 8(4): 354-358 (Liu Xuyan, Li Ping, Zhang Yanbin. Calculation of Theoretical Value of Cubic Expansion Tide and Its Harmonic Analysis[J]. Crustal Deformation and Earthquake, 1988, 8(4): 354-358)
(  0) 0) |
| [3] |
蒋骏, 张雁滨. 潮汐线应变组合观测的物理力学实质及其调和分析[J]. 地球物理学报, 1994, 37(增2): 204-212 (Jiang Jun, Zhang Yanbin. The Physics-Mechanical Significance of Tidal Strain Combination and Its Harmonic Analysis[J]. Chinese Journal of Geophysics, 1994, 37(S2): 204-212)
(  0) 0) |
| [4] |
闫伟, 牛安福, 陈国琴. 不规则载荷影响地表近场垂向位移和倾斜观测的定量计算[J]. 中国地震, 2015, 31(2): 297-307 (Yan Wei, Niu Anfu, Chen Guoqin. Calculation of Ground Vertical Displacements, Tilts and Their Distribution Characteristics around an Irregularly Load[J]. Earthquake Research in China, 2015, 31(2): 297-307)
(  0) 0) |
| [5] |
邱泽华. 钻孔应变观测点到地面载荷干扰源最小"安静"距离的理论分析[J]. 岩石力学与工程学报, 2004, 23(23): 4 063-4 067 (Qiu Zehua. Theoretic Studies on the Shortest 'Quiet' Distance between Borehole Strain Observatory Site and Surficial Mechanical Disturbance Sources[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(23): 4 063-4 067)
(  0) 0) |
| [6] |
倪红玉, 洪德全, 刘泽民, 等. 安徽地区震源机制解与应力场特征研究[J]. 大地测量与地球动力学, 2017, 37(增2): 76-80 (Ni Hongyu, Hong Dequan, Liu Zemin, et al. Research on Focal Mechanism Solutions and Characteristics of Stress Field of Anhui Region[J]. Journal of Geodesy and Geodynamics, 2017, 37(S2): 76-80)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43

