2. 地球内部多尺度成像湖北省重点实验室,武汉市鲁磨路388号,430074;
3. 地质过程与矿产资源国家重点实验室,武汉市鲁磨路388号,430074
球谐域高斯滤波在全球大地测量与地球物理场数据的平滑与去噪处理方面具有广泛的应用[1-3],但高斯滤波球谐系数递归算法[4]对于某些滤波半径在球谐阶数高于50时具有不稳定性。因此,Chambers[5]提出近似函数法,从而避免了高阶滤波系数计算的振荡问题,但是在低阶项存在较大的计算误差。Daras等[6]提出四精度方法,朱永超等[7]也进行了双精度与四精度的重力场解算精度分析,这种扩展精度方法能够在一定程度上克服高斯滤波球谐系数递归计算的不稳定性问题,但是依然无法得到本质上的解决。Piretzidis等[8-10]提出基于后向递推的连分式算法和扫描算法,但也存在低阶项权重系数振荡现象。对于后向递推,即从尾阶项由后向前递推到零值项,虽然摆脱了高阶系数计算结果的正负振荡问题,但是计算结果可能出现低阶项数值过大而无法计算的问题,如果超过规范化双精度浮点类型数值范围限制,计算编译时会出现溢出错误,而Fukushima[11-12]提出的扩展指数法可以有效解决数值溢出计算问题。
基于以上研究,本文拟采用扩展指数法优化后向递推法存在的低阶系数计算溢出问题,使其适用于任何半径大小球面、任意滤波半径的超高阶高斯滤波球谐系数计算。首先,介绍基于扩展指数的高斯滤波球谐系数后向递推方法;然后,通过数值分析测试本文方法的有效性;最后,将本文方法应用于GRACE时变重力场和地球、月球高阶静态重力场球谐模型的去噪处理,并与传统方法进行比较。
1 基于扩展指数的后向递推法Jekeli[4]利用前向递归关系计算球面各向同性高斯平滑核函数的球谐系数Wl,其迭代计算公式为:
| $ \left\{\begin{array}{l} W_0=1 \\ W_1=\frac{1+\mathrm{e}^{-2 a}}{1-\mathrm{e}^{-2 a}}-\frac{1}{a} \\ W_{l+1}=-\frac{2 l+1}{a} W_l+W_{l-1} \end{array}\right. $ | (1) |
式中,a为控制高斯平滑程度的参数,l为球谐阶数。
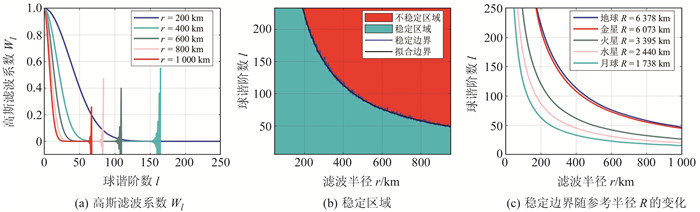
采用式(1)所示的前向递推方法计算系数Wl,可能在高阶部分存在计算不稳定性(图 1)。这是由于系数Wl本身随着阶数增高收敛于零值,但是由于普通计算机双精度浮点型数值的有效数字只能达到15~16位,从而造成接近零值的数值在计算中出现了计算误差累积。
|
图 1 前向递推法的计算结果 Fig. 1 Calculation results of forward recursion |
与前向递推不同的是,后向递推方式为从后向前,系数Wl在本质上随着阶数l增大是逐渐趋近于0值的,因此不妨选择一个较大的阶数N,令其系数值WN为0,倒数第二项系数WN-1设为一个极小的值ε,反向递推求得各项系数与W0,再逐项除以W0,即可得到最终的各项系数Wl,其递推表达式为:
| $ \left\{\begin{array}{l} W_N=0 \\ W_{N-1}=\varepsilon \\ W_{i-1}=W_{i+1}+\frac{2 l+1}{a} W_i \\ W_l=\frac{W_i}{W_0} \end{array}\right. $ | (2) |
式中,i=1, 2, 3, …, N-1。
后向递推法摆脱了高阶计算结果正负振荡的问题,但可能由于低阶项数值太大而无法计算,如果超过规范化双精度浮点类型限制,编译时就会报错。由于扩展指数法[11-12]可以摆脱计算机数值表达范围的限制,因此本文采用扩展指数与后向递推算法进行系数Wl的高精度计算。
扩展指数的基本原理可以理解为实数的表达由传统的十进制改变为BIG进制,即对于一个巨大或微小但非0的实数X,采用一个普通浮点数x和一个有符号整数ix表示并称其为X数:
| $ X=x B^{i x} $ | (3) |
式中,x为普通浮点数,B是一个人为给定的数值,ix是基数B的指数。例如,假设X=10400,若将B设置为21 000,通过式(1)转换,可得X=9.3×1098×B1,其本质就是将数值溢出B的部分变为x,同时对ix进行加减,这样,对于一个计算机无法表示的双精度浮点数,可采用多个满足表达规范的数值表示,进而解决不能采用当前的IEEE754浮点运算标准准确表示某些实数的问题。因此,扩展指数法最重要的是选择合适的基数B。
双精度浮点数能表达的最大实数约为小数点后15~16位,最大值为21 024≈1.798×10308。因此,为了计算的合理性,基数B的选取需要小于1.798×10308,同时考虑到计算的方便性,本文选取21 000≈1.0×10301作为BIG进制的基数B值。不同于Fushiman[11-12]设置B=2960≈9.75 × 10288,本文选取的基数B更大,也就意味着所能计算的数值边界更宽,例如计算最大值上限从21 024变为21 000×231。
在采用扩展指数法进行计算时,需要首先将普通实数转化为xBix的形式,然后进行X数之间的运算,最后将X数即式(2)所示的Wl计算值转化为普通实数,如此便可以解决后向递推中的数值溢出问题。本文扩展指数计算方法主要根据Fushiman[11-12]论文中附录的Fortran代码改编。
2 数值计算以地球为例,参考球面半径取6 378 km,采用一般前向递推法进行计算。结果显示,滤波半径越大,滤波系数的振荡就越早出现,如图 1(a)所示;计算的稳定区域与不稳定区域如图 1(b)所示,可见随着滤波半径r的增大,开始振荡的阶数lC与滤波半径r呈现二次函数变化特征;将一般前向递推法应用到不同行星参考球面时,随着参考球面半径R的减小,稳定区域变小,即对于相同的滤波半径r,参考球面半径越小时,会在越低的阶数开始产生振荡,如图 1(c)所示。
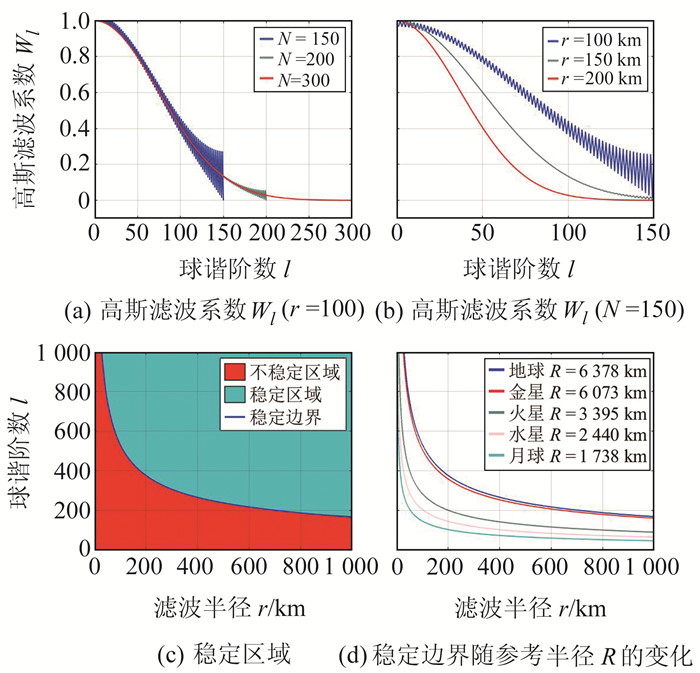
由式(2)可知,阶数N的选取会对计算结果产生影响。令N=150、200与300,参考球面半径为6 378 km,高斯滤波半径为100 km,采用一般后向递推法计算得到高斯滤波系数如图 2(a)所示,可见当阶数N选取较小时,则会在低阶部分产生振荡。固定阶数N=150,采用r=100 km、150 km与200 km的滤波半径,计算所得系数如图 2(b)所示。可见,随着滤波半径的增大,计算不稳定性逐渐消失。Piretzidis等[8-10]提出的连分式以及扫描算法的本质也是后向递推法,其计算结果与本文相似,互差数量级约10-15。造成这种低阶系数振荡的原因是低阶项数值太大,超过了规范化双精度浮点类型的限制。阶数N=150时的稳定区域和不稳定区域如图 2(c)所示。对比图 1(b)和图 2(c)发现,一般后向递推法计算的稳定区域,恰与一般前向递推法的相反,其稳定区域在上部,而前向递推的稳定区域在下部。稳定边界随不同参考球面半径的变化如图 2(d)所示。可见,对于相同的滤波半径r,参考球面半径R越小时,会在越低阶系数开始稳定。
|
图 2 后向递推法计算结果 Fig. 2 Calculation results of backward recursion |
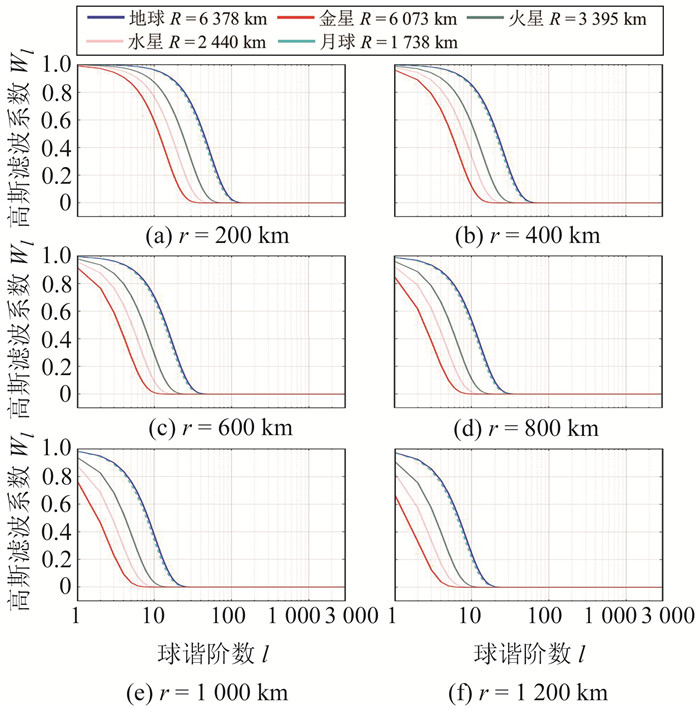
将扩展指数法应用于后向递推法的高斯滤波计算,结果如图 3所示。可以看出,该方法计算稳定,无任何振荡现象。
|
图 3 基于扩展指数与后向递推法的计算结果 Fig. 3 Calculation results of exponent extension and backward recursion |
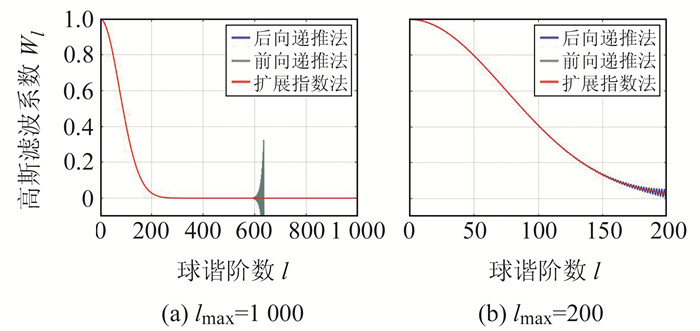
为了更直观地显示3种方法计算高斯滤波系数结果的差异,利用上述3种方法处理同一组数据:参考球面半径为6 378 km、高斯滤波半径为100 km,解算最高球谐阶数lmax分别至1 000(图 4(a))与200(图 4(b))。可以发现,当解算阶数较小时,后向递推法不稳定,在150阶以后出现明显的振荡误差,而扩展指数法和一般前向递推法稳定,二者互差数量级约为10-15;当解算阶数较大时,前向递推法计算不稳定,在约600阶开始出现振荡误差,而扩展指数法和后向递推法计算稳定,二者互差数量级约为10-15。
|
图 4 3种方法计算的高斯滤波系数Wl Fig. 4 Calculation results of Gaussian filtering coefficients (Wl) by three methods |
将本文方法分别应用于GRACE时变重力场以及地球、月球高阶静态重力场球谐模型的去噪处理,以测试其实际应用效果。
3.1 GRACE时变重力场去噪处理为研究近似计算法与球谐截断阶数法产生的误差对滤波信号的影响程度,使用GRACE-FO时变重力场球谐模型数据进行测试。
首先从ICGEM网站(http://icgem.gfz-potsdam.de/home)下载CSR(Release 6.0)96阶/次无滤波(unfiltered)的2022-01和2022-02的地球重力场球谐模型数据;然后计算得到2月相对1月的球谐系数变化数据;再采用Wahr等[13]的计算方法,将变化系数转换为地球表面质量变化,以等效水高(EWH)表示;最后采用Duan[14]的去相关滤波改进方法进行去相关滤波处理。在去相关滤波处理之后,虽然消除了大部分的南北向条带干扰,但是在赤道附近区域依然残存一些条带干扰,此外还存在全球分布的高频噪声干扰,因此需要进一步进行高斯滤波处理。
对去相关滤波处理之后的数据进一步采用基于扩展指数的后向递推法、直接截断法、近似函数法[5]分别进行高斯平滑处理,其中直接截断法是将球谐阶数截断到60阶。采用滤波半径r=200 km、500 km、800 km,基于扩展指数的后向递推法的计算结果如图 5(a)所示,直接截断法、近似函数法的计算结果与基于扩展指数后向递推法计算结果之间的差异分别见图 5(b)与图 5(c)。
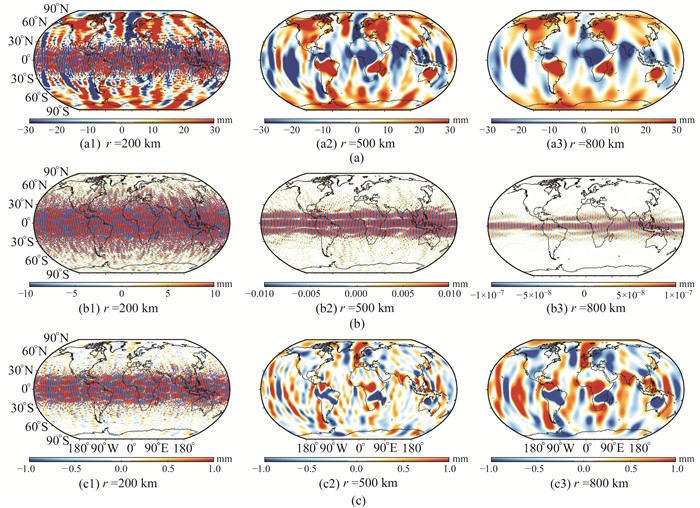
|
图 5 不同高斯滤波半径处理之后的全球EWH变化(2022-02相对2022-01)及不同方法计算结果之间的差异 Fig. 5 Global EWH changes by Gaussian filtering with different radiuses between January and February, 2022, and the difference among the calculation results by different methods |
从图 5(b)可以看出,直接截断法计算结果与基于扩展指数后向递推法计算结果之间的差异主要分布于低纬度地区。当滤波半径较小时,这种差异主要呈现为条带干扰,在高纬度地区存在部分有用信号;当滤波半径较大时,这种差异非常微弱因而可以忽略。如图 5(c)所示,近似函数法计算结果和基于扩展指数后向递推法计算结果之间的差异则分布于全球,在具有强烈的重力变化信号的地区(如格陵兰岛、南极洲、北美洲、亚马孙流域等),使用近似表达式计算所产生的误差较大,EWH误差可达1 mm左右。
为了分析近似函数法在图 5(c)中所显示的计算误差来源,计算了近似函数法与基于扩展指数后向递推法滤波系数之间的差异,如图 6所示。可以看出,近似函数法在高阶部分拟合较好,在低阶部分存在较大的拟合误差,而滤波系数低阶项的误差表现为区域性误差,因此导致了图 5(b)~(c)所示空间域差异呈现出长波长的分布特征。
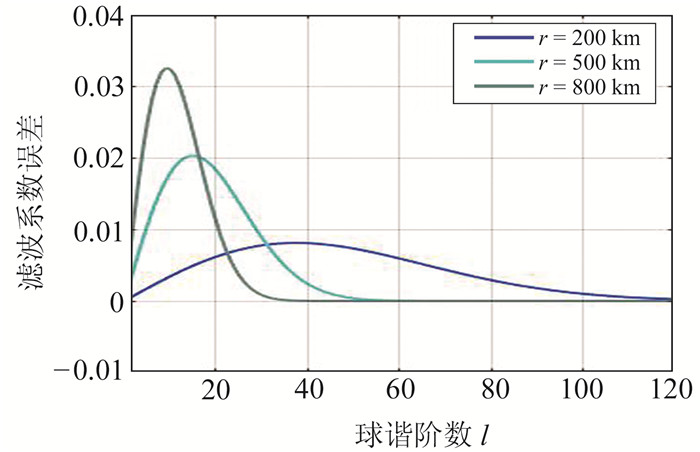
|
图 6 近似函数法与基于扩展指数后向递推法计算的高斯滤波系数之间的差异 Fig. 6 The differences of Gaussian filtering coefficients between the calculation results by approximate function and backward recursion with exponent extension |
重力观测数据不可避免地存在误差,且数据处理以及建模也会引入误差,因此一般在使用地球高阶重力场模型时需要进行一定的平滑去噪处理。
选取EIGEN-6C4模型的2~2 190阶/次球谐系数[15],扣除全球陆地与海水影响之后再进行不同半径的高斯滤波处理,解算WGS84参考椭球面上沿85°E的布格重力异常及其垂向一阶导数,解算数据间隔为0.1°,将解算结果绘制成剖面,如图 7所示。
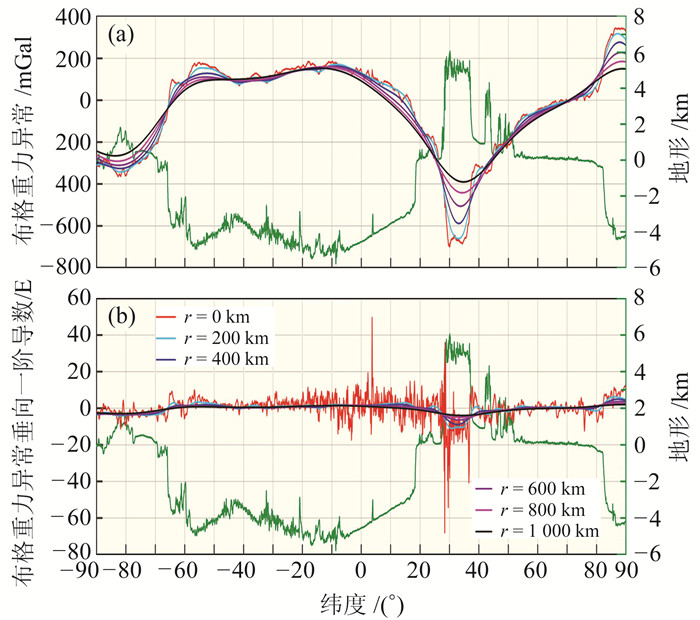
|
图 7 沿85°E不同滤波半径高斯平滑的布格重力异常及其垂向一阶导数剖面 Fig. 7 Bouguer gravity anomaly and its first-order vertical derivative profiles along 85°E by Gaussian smoothing with different filtering radii |
由图 7可以看出,布格重力异常与地形起伏存在明显的负相关性,这主要是由于地壳或岩石圈均衡所致,例如在陆地区域和海洋区域布格重力异常主体分别为负值和正值。此外,相比于布格重力异常,布格异常垂向一阶导数的趋势变化不明显而主要呈现为高频成分。当未进行高斯滤波时,布格重力异常存在大量的高频信号,这些信号可能是真实信号也可能为噪声;随着滤波半径的增大,布格重力异常越来越平滑,高频信号逐渐被压制。相比而言,随着滤波半径的增大,布格重力异常垂向一阶导数的平滑效果更加显著。
以上说明,本文所提方法对于大滤波半径的高阶滤波系数的计算是稳定且准确的,而且高斯滤波可以有效压制高阶重力场球谐模型的高频成分。
如前文所述,当参考球面半径较小时,更有可能出现高斯滤波系数计算的不稳定性。由于月球半径相比较小,因此本文也对月球高阶重力场模型进行高斯滤波处理实验。
本文采用GL1500E月球重力场模型进行去噪处理,解算阶数为2~1 500阶,计算得到月球参考球面上的重力扰动及其径向一阶导数,如图 8(a)和图 8(b)所示。可见,重力扰动存在大量的干扰,一方面表现为南北向条带特征,这主要是由卫星飞行轨道和采样点的空间分布不均匀所致,另一方面也存在由观测误差、数据处理和建模引起的高频噪声干扰。由于垂向导数计算属于高通滤波,会放大噪声干扰,因此在重力扰动的垂向一阶导数图中,干扰几乎完全掩盖了有效信号。因此,有必要对月球重力场模型进行去噪处理。
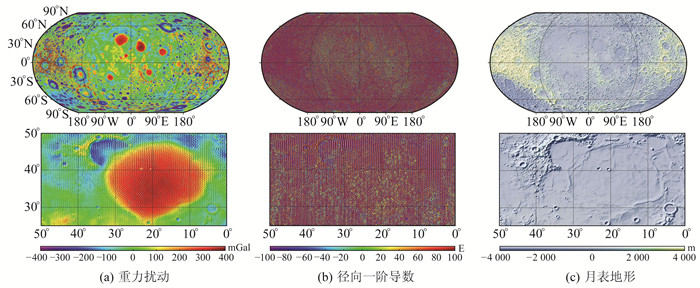
|
图 8 月球雨海区域的重力扰动及其径向一阶导数以及月表地形 Fig. 8 Gravity disturbance and its first-order radial derivative and the topography over the Mare Imbrium region of the Moon |
为了凸显滤波效果,选取干扰比较严重的雨海及其周边区域进行测试与分析。分别采用2 km、4 km、6 km、8 km、10 km与20 km的滤波半径对GL1500E模型进行高斯滤波处理,解算得到滤波之后的重力扰动及其径向一阶导数以及滤除的重力扰动信号如图 9所示。可以看出,随着滤波半径的增大,条带和噪声干扰逐渐被压制,但是同时一些有用信号也会被滤除。例如,通过与图 8(c)所示的月表地形对比可以发现,当滤波半径为6 km时,在雨海西北角区域,部分撞击坑产生的重力扰动信号也被滤除了,但是在重力扰动及其径向一阶导数图中依然残存一些干扰未被滤除。因此,在使用高斯滤波时,一方面需要结合研究目标选取合适的滤波半径,另一方面各向同性高斯平滑适合滤除高频噪声但不适合压制条带干扰。所以,一方面可以采用各向异性的高斯滤波,另一方面需要结合其他滤波方法,例如去相关滤波或方向滤波等。此外,由滤除的信号可以看出,干扰信号在空间分布上是不均匀的,因此有必要考虑空间域自适应的高斯滤波。
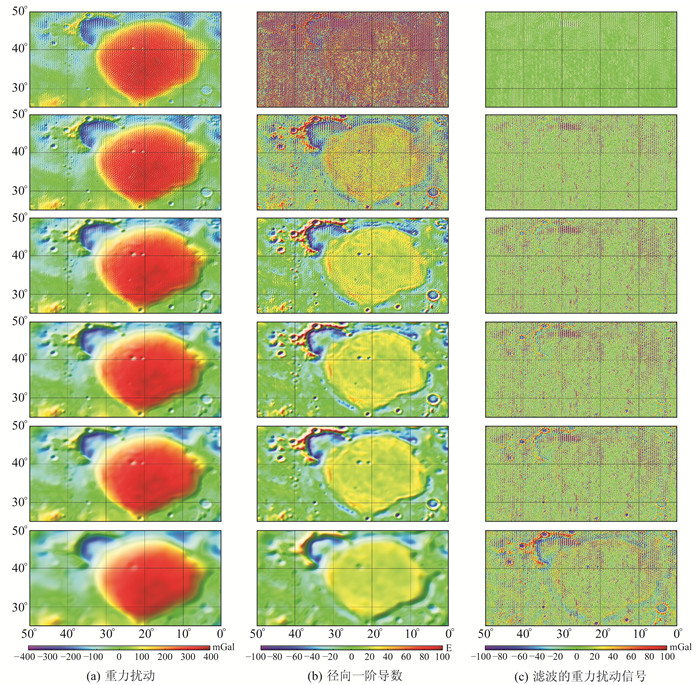
|
由上至下,高斯滤波半径依次为r=2 km、4 km、6 km、8 km、10 km与20 km 图 9 月球雨海区域不同滤波半径高斯平滑之后的重力扰动及其径向一阶导数与滤除的重力扰动信号 Fig. 9 Gravity disturbance and its first-order radial derivative and the removed gravity disturbance signals over the Mare Imbrium region by using the Gaussian smooth with different filtering radii |
针对传统球谐域高斯滤波系数计算方法中存在的不稳定性问题,提出将扩展指数法应用于滤波系数的后向递推计算之中,通过数值计算和实际应用,得到如下结论:
1) 当滤波半径较大、参考球面半径较小、球谐阶数较高时,传统的高斯滤波系数前向递推方法存在高阶部分的计算不稳定性,而后向递推方法存在低阶部分的数值溢出问题;
2) 将扩展指数法与后向递推方法相结合,基本可实现任何半径大小球面、任意滤波半径的超高阶高斯滤波高精度计算;
3) 对于GRACE时变重力场数据的高斯平滑处理,传统的近似函数法存在较大的计算误差,而对于直接截断法,当滤波半径较大时,其误差比较微弱,可以忽略;
4) 高斯滤波可以有效压制地球与月球静态高阶重力场球谐模型中的噪声干扰,但是在压制干扰的同时也会滤除部分有用信号,因此在实际应用中应结合研究目标选取合适的滤波半径;
5) 各向同性高斯平滑适合滤除高频噪声但不适合压制条带干扰,需要结合其他针对条带干扰的滤波方法进行组合处理。此外,地球与月球重力场球谐模型中的噪声往往不是均匀分布的,因此需要发展空间域自适应的高斯滤波方法。
致谢: GRACE Follow-On每月的地球重力场与EIGEN-6C4高阶地球重力场球谐模型数据均取自International Centre for Global Earth Models,GL1500E月球重力场球谐模型数据来源于NASA PDS Geoscience Node Data,球面投影图件采用Generic Mapping Tools(GMT)软件进行绘制,在此一并表示感谢!
| [1] |
周新, 邢乐林, 邹正波, 等. GRACE时变重力场的高斯平滑研究[J]. 大地测量与地球动力学, 2008, 28(3): 41-45 (Zhou Xin, Xing Lelin, Zou Zhengbo, et al. Study on Gaussian Smoothing of GRACE Temporal Gravity Variation[J]. Journal of Geodesy and Geodynamics, 2008, 28(3): 41-45)
(  0) 0) |
| [2] |
郗慧, 张子占, 陆洋, 等. 利用GRACE监测全球海水质量变化时滤波处理的影响分析[J]. 大地测量与地球动力学, 2016, 36(5): 380-385 (Xi Hui, Zhang Zizhan, Lu Yang, et al. The Performances of Different Filtering Methods on Ocean Mass Change Estimated from GRACE[J]. Journal of Geodesy and Geodynamics, 2016, 36(5): 380-385)
(  0) 0) |
| [3] |
孙文科, 长谷川崇, 张新林, 等. 高斯滤波在处理GRACE数据中的模拟研究: 西藏拉萨的重力变化率[J]. 中国科学: 地球科学, 2022, 54(9): 1 327-1 333 (Sun Wenke, Hasegawa T, Zhang Xinlin, et al. Simulation Study of Gaussian Filter in Processing GRACE Data: Gravity Change Rate in Lhasa, Tibet[J]. Science China: Earth Sciences, 2022, 54(9): 1 327-1 333)
(  0) 0) |
| [4] |
Jekeli C. Alternative Methods to Smooth the Earth's Gravity Field[R]. Ohio State University, 1981
(  0) 0) |
| [5] |
Chambers D P. Observing Seasonal Steric Sea Level Variations with GRACE and Satellite Altimetry[J]. Journal of Geophysical Research: Oceans, 2006, 111(C3)
(  0) 0) |
| [6] |
Daras I, Pail R, Murböck M, et al. Gravity Field Processing with Enhanced Numerical Precision for LL-SST Missions[J]. Journal of Geodesy, 2015, 89(2): 99-110 DOI:10.1007/s00190-014-0764-2
(  0) 0) |
| [7] |
朱永超, 万晓云, 周保兴. 基于双精度与四精度的重力场解算精度分析[J]. 大地测量与地球动力学, 2020, 40(1): 94-97 (Zhu Yongchao, Wan Xiaoyun, Zhou Baoxing. Accuracy Analysis of the Double Precision and Quadruple Precision Gravity Field Solution[J]. Journal of Geodesy and Geodynamics, 2020, 40(1): 94-97)
(  0) 0) |
| [8] |
Piretzidis D, Sideris M G. Stable Recurrent Calculation of Isotropic Gaussian Filter Coefficients[J]. Computers and Geosciences, 2019, 133
(  0) 0) |
| [9] |
Piretzidis D, Sideris M G. Additional Methods for the Stable Calculation of Isotropic Gaussian Filter Coefficients: The Case of a Truncated Filter Kernel[J]. Computers and Geosciences, 2020, 145
(  0) 0) |
| [10] |
Piretzidis D, Sideris M G. Expressions for the Calculation of Isotropic Gaussian Filter Kernels in the Spherical Harmonic Domain[J]. Studia Geophysica et Geodaetica, 2022, 66: 1-22 DOI:10.1007/s11200-021-0272-9
(  0) 0) |
| [11] |
Fukushima T. Numerical Computation of Spherical Harmonics of Arbitrary Degree and Order by Extending Exponent of Floating Point Numbers[J]. Journal of Geodesy, 2012, 86: 271-285
(  0) 0) |
| [12] |
Fukushima T. Numerical Computation of Spherical Harmonics of Arbitrary Degree and Order by Extending Exponent of Floating Point Numbers: Ⅱ First-, Second-, and Third-Order Derivatives[J]. Journal of Geodesy, 2012, 86: 1 019-1 028
(  0) 0) |
| [13] |
Wahr J, Molenaar M, Bryan F. Time Variability of the Earth's Gravity Field: Hydrological and Oceanic Effects and Their Possible Detection Using GRACE[J]. Journal of Geophysical Research: Solid Earth, 1998, 103(B12): 30 205-30 230
(  0) 0) |
| [14] |
Duan X J, Guo J Y, Shum C K, et al. On the Postprocessing Removal of Correlated Errors in GRACE Temporal Gravity Field Solutions[J]. Journal of Geodesy, 2009, 83(11): 1 095
(  0) 0) |
| [15] |
Förste C, Bruinsma S L, Abrykosov O, et al. EIGEN-6C4 the Latest Combined Global Gravity Field Model Including GOCE Data up to Degree and Order 2 190 of GFZ Potsdam and GRGS Toulouse[C]. EGU Generd Assemnly Conference, Vienna, 2014
(  0) 0) |
2. Hubei Subsurface Multi-Scale Imaging Key Laboratory, 388 Lumo Road, Wuhan 430074, China;
3. State Key Laboratory of Geological Processes and Mineral Resources, 388 Lumo Road, Wuhan 430074, China
 2023, Vol. 43
2023, Vol. 43


