2. 武汉大学测绘学院,武汉市珞喻路129号,430079
由于采用的时变重力场模型的反演方法及背景模型存在差异,利用不同机构发布的GRACE/GRACE-FO时变重力场模型反演的陆地水储量变化也存在不同[1]。因此,需要对模型精度进行评估,以了解不同机构模型反演的陆地水储量变化的不确定性。GRACE/GRACE-FO时变重力场模型反演的陆地水储量包含土壤水、河流及湖泊等地表信号和地下水等信号,由于缺乏与其对应的全球尺度的实测数据,因此精度评定是GRACE/GRACE-FO数据处理的难点之一。万祥禹等[2]利用水文模型验证GRACE/GRACE-FO反演陆地水储量变化的精度,但受限于水文模型精度及缺少地下水变化分量,导致模型不确定性估计不准确;Swenson等[3]利用水井、河流径流实测数据开展局部流域的不确定性评估,但该方法需要大量的实测数据,不适用于全球尺度或缺乏水文观测数据区域的不确定性评估。为了增强精度评价方法的普适性,研究人员提出利用方差分量估计、公海残差、空间协方差和广义三角帽等方法评估重力卫星反演的陆地水储量变化的不确定性[4-8]。其中,三角帽方法最初设计是用于估计振荡器和计时设备的相对精度,该方法依赖于从观测数据中去除共同信号(即真实信号),然后提供反映测量误差的不确定度,已广泛应用于卫星重力研究。Ferreira等[7]首先利用广义三角帽方法估计CSR RL05、JPL RL05、GFZ RL05和GRGS球谐系数模型的不确定性;姚朝龙等[8]利用相同方法评估5种GRACE时变重力场模型反演中国大陆地区2003~2013年陆地水储量变化的不确定性;Chen等[5]结合公海残差和三角帽方法对GRACE/GRACE-FO官方数据中心发布的RL06版本重力场模型反演的全球尺度的地表质量变化进行全面的误差评估。最新发布的RL06时变重力场模型采用新的数据处理方法,模型整体精度较早期版本有较明显提升,其中CSR RL06模型全球尺度的信噪比优于其他模型[9]。同时,Meyer等[10]采用方差分量估计融合多个机构发布的模型得到COST-G月时变模型,其噪声水平较低。
综上所述,目前缺乏针对最新版本的重力场模型在流域尺度上的不确定性评估的研究,有必要开展相关工作并分析流域陆地水储量不确定性的特点。本文采用广义三角帽方法评估CSR RL06、JPL RL06、GFZ RL06、ITSG-Grace2018和COST-G时变重力场模型反演流域陆地水储量变化的不确定性,并探讨地理位置、气候类型和流域面积对不确定性的影响。
1 广义三角帽法原理假设流域陆地水储量变化时间序列为:
| $ \boldsymbol{X}_i=\boldsymbol{X}_{\text {true }}+\boldsymbol{e}_i, i=1,2, \cdots, N $ | (1) |
式中,Xtrue为流域陆地水储量变化的真值,ei为第i个模型的陆地水储量变化时间序列的误差,N为时变重力场模型个数。
一般地,Xtrue可以用水文模型或水井测量等实测数据替代,但这种方案存在明显缺陷:水文模型及实测数据并非陆地水储量的直接观测量且有一定的不确定性,同时,多数流域并不能够提供全流域尺度的实测数据。因此,大部分流域的陆地水储量变化的真值是未知的。三角帽方法可以在实际陆地水储量变化未知的情况下,通过差分来估计至少3组模型之间的相对不确定性。这里选择某一观测序列作为参考场作差得[11]:
| $ \begin{gathered} \boldsymbol{Y}_{i, N}=\boldsymbol{X}_i-\boldsymbol{X}_N=\boldsymbol{e}_i-\boldsymbol{e}_N, \\ i=1,2, \cdots, N-1 \end{gathered} $ | (2) |
式中,Y为M×(N-1)维矩阵,M为时间序列期数。因参考场的选取不影响最终的不确定性结果[7],本文选择COST-G时间序列作为参考场。矩阵Y的协方差矩阵S=cov(Y)可以通过引入噪声矩阵R表示[12]:
| $ \boldsymbol{S}=\boldsymbol{J} \cdot \boldsymbol{R} \cdot \boldsymbol{J}^{\mathrm{T}} $ | (3) |
其中,
| $ \boldsymbol{J}_{N-1, N}=\left[\begin{array}{ccccc} 1 & 0 & \vdots & 0 & -1 \\ 0 & 1 & \vdots & 0 & -1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & -1 \end{array}\right] $ | (4) |
通过引入基于Kuhn-Tucker理论提出的目标函数和约束求解欠定方程组(3)[13]:
| $ \boldsymbol{G}\left(r_{1 N}, r_{2 N}, \cdots, r_{N N}\right)=\frac{1}{\boldsymbol{K}^2} \sum\limits_{i < j}^N r_{i j}^2 $ | (5) |
| $ \boldsymbol{H}\left(r_{1 N}, r_{2 N}, \cdots, r_{N N}\right)=-\frac{|\boldsymbol{R}|}{|\boldsymbol{S}| \cdot \boldsymbol{K}}<0 $ | (6) |
式中,
| $ \left\{\begin{array}{l} r_{1 N}^0=0, i<N \\ r_{N N}^0=\frac{1}{2 \boldsymbol{S}^*}, \boldsymbol{S}^*=\left[\begin{array}{llll} 1 & 1 & \cdots & 1 \end{array}\right] \boldsymbol{S}^{-1}\left[\begin{array}{llll} 1 & 1 & \cdots & 1 \end{array}\right]^{\mathrm{T}} \end{array}\right. $ | (7) |
根据约束条件,通过最小化目标函数来获得N个自由参数。每组陆地水储量变化时间序列的不确定性通过标准偏差表示,即
选择CSR RL06、JPL RL06、GFZ RL06、ITSG-Grace2018和COST-G等5个GRACE/GRACE-FO月时变重力场模型2002-04~2021-12的数据进行处理。其中,除COST-G(来自90阶球谐系数截断到60阶)外,其他模型均采用官方提供的60阶球谐系数模型。对所有模型采用相同的数据处理策略:利用卫星激光测距结果替换时变重力场模型中的C20和C30项[15-16],将利用GRACE-OBP反演得到的一阶项球谐系数加入时变重力场模型[17],并利用ICE-6G_D(VM5a)冰后回弹模型扣除GIA影响[18]。通常情况下,需要对时变重力场模型进行滤波处理来抑制高频噪声和南北条带误差。为了准确评估模型不确定性,对不同滤波处理下的模型不确定性进行分析,发现滤波处理方法对最终的模型相对不确定性影响较小,与Chen等[5]研究结果一致。限于篇幅,以最常用的300 km高斯平滑[19]和P4M6去相关滤波[20]组合滤波算法反演的全球地表质量变化结果为例,统计流域陆地水储量变化,并开展不确定性评估。
2.2 研究区域根据流域面积选取全球前60个流域作为研究区域开展时变重力场模型不确定性评估,流域总面积约为61.3×106 km2,占全球陆地总面积的41%,其空间分布如图 1所示。为了分析流域面积和气候类型对流域陆地水储量变化不确定性的影响,根据面积将流域划分为不同等级,同时利用年平均干旱指数将流域划分为干旱(A)、半干旱(SA)、半湿润(SH)和湿润(H)4种气候类型。
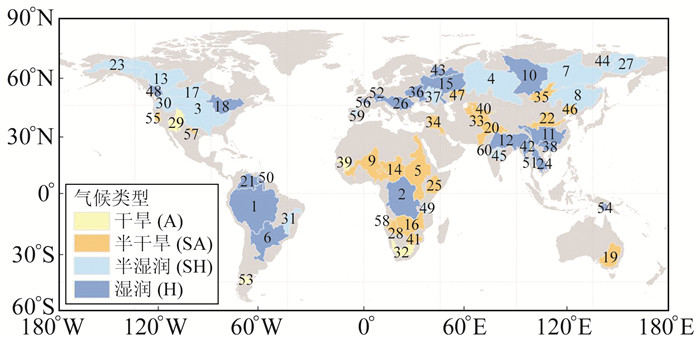
|
大尺度流域: 1亚马孙 2扎伊尔 3密西西比 4鄂毕 5尼罗 6巴拉那 7勒拿 8阿穆尔 9尼日尔 10叶尼塞 11长江 12恒河-布拉马普特拉 13麦肯齐 14乍得湖 15伏尔加 16赞比亚 17萨斯喀彻温-尼尔森 18圣劳伦斯 19墨累-达令 20印度 21奥里诺科 22黄河 23育空 24湄公河 25朱巴-谢贝利 26多瑙河 27科雷马 28奥卡万戈 29科罗拉多 30哥伦比亚 中尺度流域: 31圣弗朗西斯科 32奥兰治 33阿姆 34底格里斯-幼发拉底 35贝加尔湖 36第聂伯 37顿河 38珠江 39塞内加尔 40锡尔 41林波波 42伊洛瓦底 43西德维纳 44因迪吉尔卡 45戈达瓦里 46辽河 47乌拉尔 48弗雷泽 49鲁菲吉 50埃塞奎博 小尺度流域: 51湄南河 52莱茵 53丘布特 54弗莱 55萨克拉门托 56卢瓦尔 57科罗拉多河 58库内纳 59杜罗 60讷尔默博 图 1 流域空间分布及气候类型 Fig. 1 Spatial distribution and climate type of basins |
利用广义三角帽法开展不确定性评估的基本假设是不同模型间具有相同的真实信号和独立的噪声[13],本文利用不同时变重力场模型在球谐域内的皮尔逊相关系数对基本假设进行检验,结果如图 2所示。由于P4M6去相关滤波不适用于阶次均大于50的球谐系数[20],故剔除该部分球谐系数(图 2子图中左、右下角部分)。由图可知,不同机构球谐系数模型在低阶/低次区域(约 < 25)表现出较好的一致性,相关系数接近1;随着阶次的增加,不同模型间的相关性降低。将某次所有阶的球谐系数相关系数取平均得到次相关系数,统计表明,不同模型间的次相关系数随着次的增加而显著减小。考虑到随着阶次的增加,球谐系数中的信噪比将显著降低,结合高阶次球谐系数间的相关性较弱进行分析可知,不同模型的球谐系数误差总体属于随机噪声,基本满足广义三角帽法评估模型不确定性的前提假设。
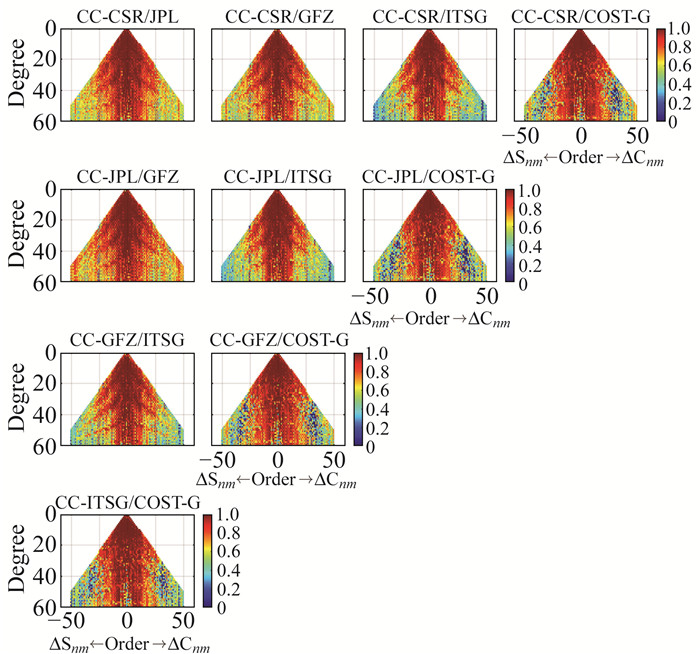
|
图 2 球谐系数模型在谱域上的相关系数 Fig. 2 Correlation coefficient of spherical harmonic coefficient models in the spectral domain |
表 1为利用广义三角帽方法计算的不同模型的流域陆地水储量变化的标准偏差(粗体表示最低不确定性,下划线表示最高不确定性)。对于绝大多数流域而言,COST-G模型反演的流域陆地水储量变化的标准偏差明显低于其他模型,且27个流域的不确定性小于0.3 cm;CSR和JPL的不确定性基本小于0.8 cm,但在部分流域的不确定性偏大,如JPL模型在弗莱(54号)流域的不确定性达到1.34 cm;ITSG模型反演的流域不确定性略高于CSR和JPL模型,约有12个流域陆地水储量变化的不确定性大于1.0 cm;GFZ模型反演的流域陆地水储量变化不确定性最大,约有24个流域的不确定性超过1.0 cm。若取所有流域的平均标准偏差作为模型的总体不确定性,则COST-G、CSR、JPL、ITSG和GFZ模型的不确定性分别为0.41 cm、0.63 cm、0.66 cm、0.81 cm和0.97 cm。整体而言,COST-G模型反演的流域陆地水储量变化具有最低的不确定性。
|
|
表 1 不同时变重力场模型的流域陆地水储量变化不确定性 Tab. 1 Uncertainties of basin terrestrial water storage changes for different time-varying gravity field models |
图 3为流域陆地水储量变化不确定性的空间分布图。可以看出,除COST-G模型外,其他4个时变重力场模型的不确定性具有较强的区域性,可能因为COST-G模型为根据方差分量估计通过多个时变重力场模型加权得到,其不确定性对流域的位置并不敏感。表 2统计了各模型在不同区域的最高和最低不确定性的流域个数,同时标记非组合模型外的4个模型统计结果。可以看出,COST-G模型在全球流域范围内具有较高的精度,但对于个别流域如非洲的林波波(41号)流域和库内纳(58号)流域的不确定性高于其他模型。对于非组合模型来说,CSR和JPL模型反演流域陆地水储量变化的不确定性较低,其中CSR模型在北美流域反演结果较好,在南美洲JPL模型整体精度较好。ITSG和GFZ模型反演结果不确定性较大,其中,GFZ模型在北美及欧洲流域表现较差,部分流域陆地水储量变化的标准偏差超过1.3 cm;ITSG模型在南美流域具有较高的不确定性,如在亚马孙流域的标准偏差是CSR和JPL模型标准偏差的2倍。
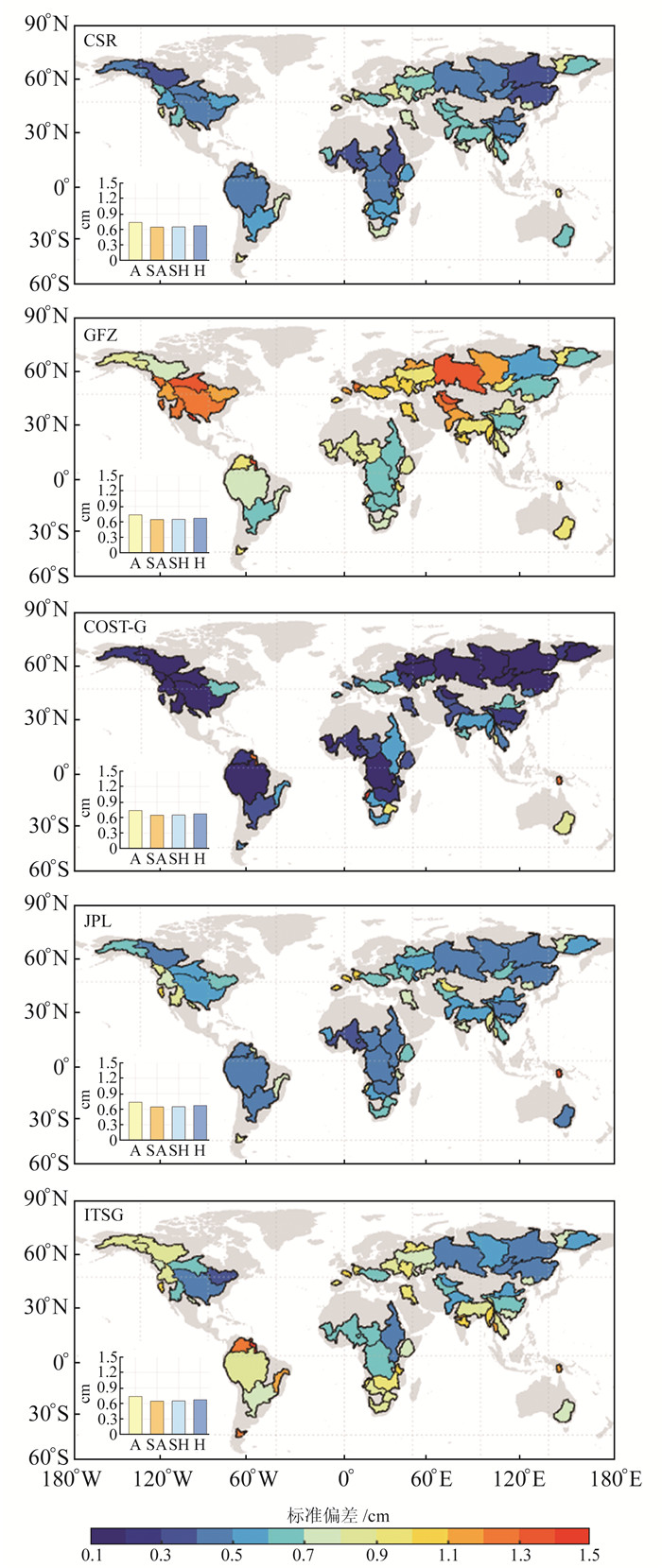
|
图 3 流域标准偏差空间分布及不同气候类型下的流域不确定性 Fig. 3 Spatial distribution of basin standard deviations and basin uncertainty under different climate types |
|
|
表 2 各模型在不同区域具有最高最低不确定性的流域个数 Tab. 2 The numbers of basins with the highest and lowest uncertainty for each model in different regions |
为分析不同气候类型下的时变重力场模型不确定性,将相同气候类型的流域不确定性取平均作为该气候类型的不确定性结果(图 3)。分析可知,对于不同模型反演结果,不同气候类型的平均不确定性排序存在差异且无明显规律,即CSR: A>H>SA>SH; JPL: A>H>SH>SA; GFZ: H>SA>SH>A; ITSG: A>H>SH>SA; COST-G: SA>H>A>SH,表明流域陆地水储量的不确定性受流域气候类型的影响较小。为分析流域面积对流域陆地水储量变化不确定性的影响,将流域按照面积大小进行排序并绘制流域面积-流域不确定性图(图 4)。可以看出,流域面积与陆地水储量变化的不确定性具有较强的相关性,不确定性随流域面积的减小而增大。
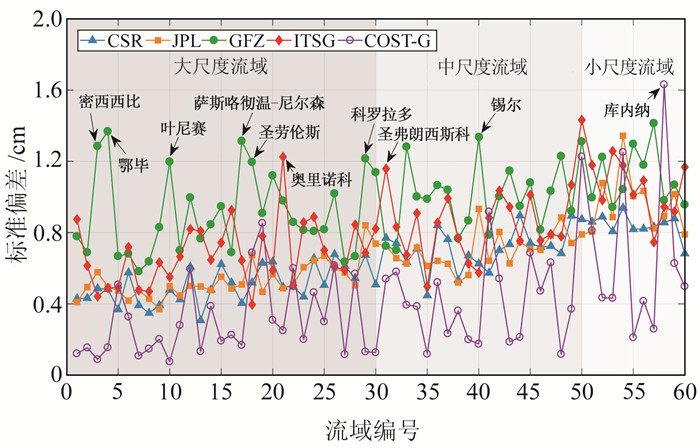
|
图 4 流域面积与流域陆地水储量变化不确定性 Fig. 4 Basin area and uncertainties of basin terrestrial water storage changes |
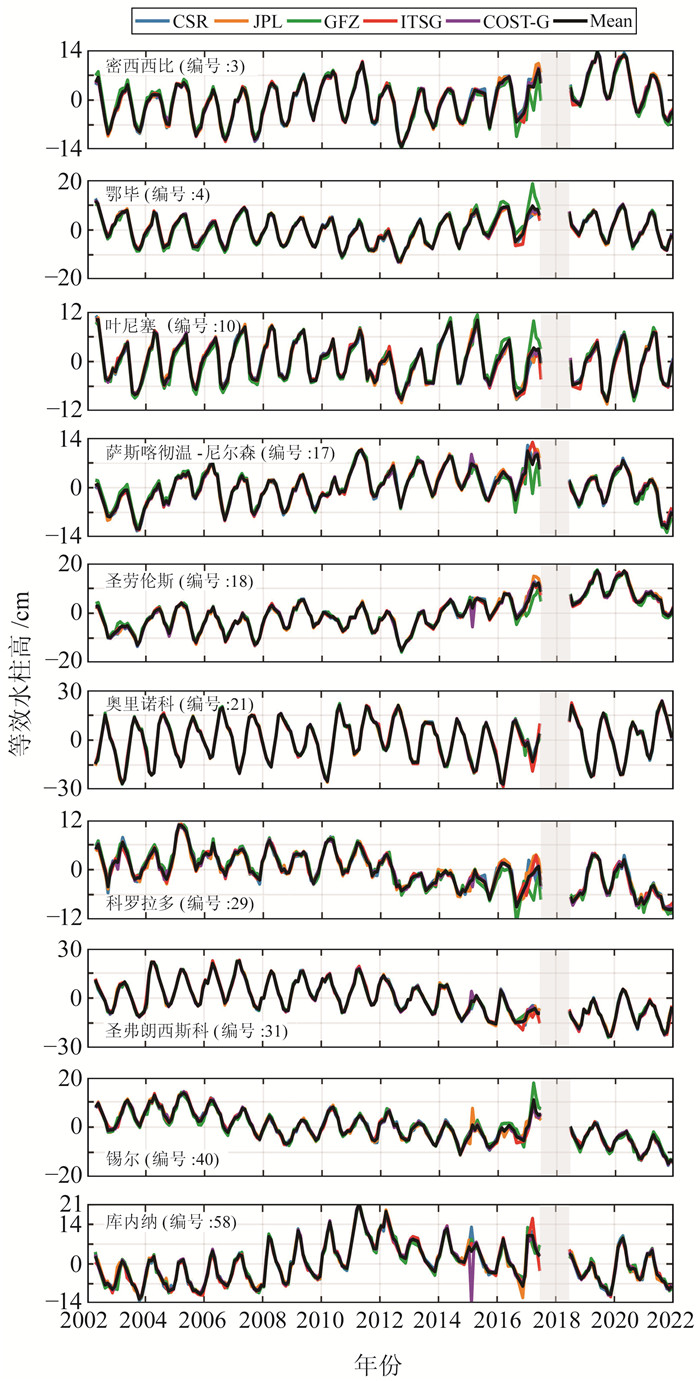
由图 4可发现,对于少数流域而言,不同时变重力场模型之间存在明显差异,如GFZ模型在密西西比流域(3号)和鄂毕流域(4号)的标准偏差明显高于其他模型。因此,利用流域时间序列分析不确定性异常的原因。图 5为选取流域的时间序列曲线,同时取不同模型时间序列的平均值作为参照。由图可知,在通常情况下,不同模型的反演结果一致性较好,但是在GRACE后期则存在显著差异。当GFZ显示出最大的不确定性时(3、4、10、17、18、29、40号),GFZ相对于平均时间序列的差异最大;当ITSG显示出最大的不确定性时(21、31号),ITSG相对于平均时间序列的差异最大。COST-G模型2015-02在库内纳(8号)流域存在明显异常变化,导致其在该流域的不确定性偏大;另外,COST-G模型在萨斯喀彻温-尼尔森(17号)流域、圣劳伦斯(18号)流域、JPL模型在锡尔(40号)流域的同期数据同样表现出异常变化。这可能是由于当期数据质量较差(如短周期重复轨道、GRACE单加速度计、仪器老化等),各个机构对此类数据的处理策略不同,从而导致反演的流域陆地水储量变化的不确定性较大。COST-G模型2015-02的球谐系数是由CSR、GFZ、ITSG和无约束GRGS模型加权得到,由图 5可见,CSR、GFZ和ITSG模型的库内纳(58号)流域时间序列并未出现异常信号,因此推测,GRGS模型可能是COST-G模型在该流域出现信号异常的主要原因。
|
图 5 典型流域的陆地水储量变化时间序列 Fig. 5 Time series of terrestrial water storage changes in typical basins |
利用广义三角帽方法评估5种最新GRACE/GRACE-FO时变重力场模型反演的全球流域陆地水储量变化的不确定性,并探讨地理位置、气候类型和流域面积对不确定性的影响。主要的研究结果表明:
1) COST-G、CSR、JPL、ITSG和GFZ时变重力场模型反演全球60个流域的陆地水储量变化的平均不确定性分别是0.41 cm、0.63 cm、0.66 cm、0.81 cm和0.97 cm,组合模型COST-G反演结果的不确定性最低,GFZ模型精度最差。单一模型CSR、JPL、ITSG和GFZ具有较强的区域相关性。流域陆地水储量变化的不确定性与流域面积存在较强的相关性,而与气候类型的相关性较小。
2) 通常情况下,不同模型反演的陆地水储量变化具有较高的一致性,但当观测数据质量较差时,不同机构对数据处理的策略存在差异,从而导致不同模型反演的流域陆地水储量变化存在较大差异。虽然COST-G模型在全球尺度上具有较低的标准偏差,但若融合模型中的个别模型存在系统偏差则会导致其结果存在异常,进而严重影响COST-G模型反演的流域陆地水储量变化的不确定性。因此,在进行流域陆地水储量计算时,应开展多模型反演结果对比以选择合适的模型。
| [1] |
Sakumura C, Bettadpur S, Bruinsma S. Ensemble Prediction and Intercomparison Analysis of GRACE Time-Variable Gravity Field Models[J]. Geophysical Research Letters, 2014, 41(5): 1 389-1 397 DOI:10.1002/2013GL058632
(  0) 0) |
| [2] |
万祥禹, 游为, 王海波, 等. 基于多源数据分析维多利亚湖流域水储量变化[J]. 地球物理学报, 2021, 64(2): 441-454 (Wan Xiangyu, You Wei, Wang Haibo, et al. Terrestrial Water Storage Variations in Lake Victoria Basin from Multi-Source Data[J]. Chinese Journal of Geophysics, 2021, 64(2): 441-454)
(  0) 0) |
| [3] |
Swenson S, Yeh P J F, Wahr J, et al. A Comparison of Terrestrial Water Storage Variations from GRACE with in Situ Measurements from Illinois[J]. Geophysical Research Letters, 2006, 33(16)
(  0) 0) |
| [4] |
Ditmar P. How to Quantify the Accuracy of Mass Anomaly Time-Series Based on GRACE Data in the Absence of Knowledge about True Signal[J]. Journal of Geodesy, 2022, 96(8): 54 DOI:10.1007/s00190-022-01640-x
(  0) 0) |
| [5] |
Chen J L, Tapley B, Tamisiea M E, et al. Error Assessment of GRACE and GRACE Follow-on Mass Change[J]. Journal of Geophysical Research: Solid Earth, 2021, 126(9)
(  0) 0) |
| [6] |
Boergens E, Kvas A, Eicker A, et al. Uncertainties of GRACE-Based Terrestrial Water Storage Anomalies for Arbitrary Averaging Regions[J]. Journal of Geophysical Research: Solid Earth, 2022, 127(2)
(  0) 0) |
| [7] |
Ferreira V G, Montecino H D C, Yakubu C I, et al. Uncertainties of the Gravity Recovery and Climate Experiment Time-Variable Gravity-Field Solutions Based on Three-Cornered Hat Method[J]. Journal of Applied Remote Sensing, 2016, 10(1)
(  0) 0) |
| [8] |
姚朝龙, 李琼, 罗志才, 等. 利用广义三角帽方法评估GRACE反演中国大陆地区水储量变化的不确定性[J]. 地球物理学报, 2019, 62(3): 883-897 (Yao Chaolong, Li Qiong, Luo Zhicai, et al. Uncertainties in GRACE-Derived Terrestrial Water Storage Changes over Chinese Mainland Based on a Generalized Three-Cornered Hat Method[J]. Chinese Journal of Geophysics, 2019, 62(3): 883-897)
(  0) 0) |
| [9] |
郭飞霄, 孙中苗, 任飞龙, 等. GRACE RL06与RL05时变重力场模型数据初步比较分析[J]. 大地测量与地球动力学, 2020, 40(5): 546-550 (Guo Feixiao, Sun Zhongmiao, Ren Feilong, et al. Preliminary Comparative Analysis of GRACE RL06 and RL05 Time-Variable Gravity Models[J]. Journal of Geodesy and Geodynamics, 2020, 40(5): 546-550)
(  0) 0) |
| [10] |
Meyer U, Jean Y, Kvas A, et al. Combination of GRACE Monthly Gravity Fields on the Normal Equation Level[J]. Journal of Geodesy, 2019, 93(9): 1 645-1 658 DOI:10.1007/s00190-019-01274-6
(  0) 0) |
| [11] |
Koot L, Viron O, Dehant V. Atmospheric Angular Momentum Time-Series: Characterization of Their Internal Noise and Creation of a Combined Series[J]. Journal of Geodesy, 2006, 79(12): 663-674 DOI:10.1007/s00190-005-0019-3
(  0) 0) |
| [12] |
Galindo F J, Palacio J. Post-Processing ROA Data Clocks for Optimal Stability in the Ensemble Timescale[J]. Metrologia, 2003, 40(3): S237-S244 DOI:10.1088/0026-1394/40/3/301
(  0) 0) |
| [13] |
Galindo F J, Palacio J. Estimating the Instabilities of N Correlated Clocks[C]. 31st Annual Precise Time and Time Interval Meeting, Dana Point, 1999
(  0) 0) |
| [14] |
Tavella P, Premoli A. Estimating the Instabilities of N Clocks by Measuring Differences of Their Readings[J]. Metrologia, 1994, 30(5): 479-486 DOI:10.1088/0026-1394/30/5/003
(  0) 0) |
| [15] |
Loomis B D, Rachlin K E, Luthcke S B. Improved Earth Oblateness Rate Reveals Increased Ice Sheet Losses and Mass-Driven Sea Level Rise[J]. Geophysical Research Letters, 2019, 46(12): 6 910-6 917 DOI:10.1029/2019GL082929
(  0) 0) |
| [16] |
Loomis B D, Rachlin K E, Wiese D N, et al. Replacing GRACE/GRACE-FO C30 With Satellite Laser Ranging: Impacts on Antarctic Ice Sheet Mass Change[J]. Geophysical Research Letters, 2020, 47(3)
(  0) 0) |
| [17] |
Sun Y, Riva R, Ditmar P. Optimizing Estimates of Annual Variations and Trends in Geocenter Motion and J2 from a Combination of GRACE Data and Geophysical Models[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(11): 8 352-8 370 DOI:10.1002/2016JB013073
(  0) 0) |
| [18] |
Peltier W R, Argus D F, Drummond R. Comment on "An Assessment of the ICE-6G_C(VM5a) Glacial Isostatic Adjustment Model" by Purcell et al[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(2): 2 019-2 028 DOI:10.1002/2016JB013844
(  0) 0) |
| [19] |
Wahr J, Molenaar M, Bryan F. Time Variability of the Earth's Gravity Field: Hydrological and Oceanic Effects and Their Possible Detection Using GRACE[J]. Journal of Geophysical Research: Solid Earth, 1998, 103(B12): 30 205-30 230 DOI:10.1029/98JB02844
(  0) 0) |
| [20] |
Chen J L, Wilson C R, Tapley B D, et al. GRACE Detects Coseismic and Postseismic Deformation from the Sumatra-Andaman Earthquake[J]. Geophysical Research Letters, 2007, 34(13)
(  0) 0) |
2. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2023, Vol. 43
2023, Vol. 43


