钻孔体应变仪传感器的工作环境在地下,仪器与围岩的耦合系数是影响应变观测精度的重要因素。计算耦合系数的常用方法有两类,一类是基于弹性力学理论,建立一个合理的理论模型,诸如双环模型、两层介质模型和双衬套模型等,采用正演的方法计算耦合系数[1-2]。然而实际计算过程中,钻孔岩芯的弹性模量和泊松比等相关力学参数多是采用岩性的平均弹性模量,并不能真实地反映钻孔应变周围的岩芯特性。另一类方法是基于固体潮汐变形理论,采用钻孔应变的观测值实地标定对耦合系数进行修正[3-4]。然而,由于实测耦合系数与观测数据的固体潮汐形态呈正相关,很难独立了解钻孔的真实耦合情况。
本文对江苏省不同地区的体应变钻孔岩芯进行系统性的单轴压缩实验,获取不同地区钻孔岩芯的弹性模量和泊松系数[5-6],再采用不同方法计算钻孔的耦合系数,对仪器观测精度进行相关性分析,以期得到井孔耦合程度的定量化评定指标,进一步探讨耦合系数对观测精度影响的阈值。
1 单轴压缩实验 1.1 实验样品与制备实验样品为江苏省在运行的TJ-2型体应变仪的钻孔岩芯,台站分布见图 1。TJ-2型体应变仪的传感器为一个充满了硅油的长圆形弹性筒。根据《DB/T 8.2-2020地震台站建设规范——地形变台站第2部分:钻孔地倾斜和地应变台站》要求,体应变仪安装时需要进行钻孔工程的施工:松散层孔段采用正循环无芯钻进,岩石井段采用Ø159 mm金刚石取芯钻头取芯钻进。根据岩芯的致密性进一步确定准确的安装位置,利用水泥将传感器和四周岩石紧密耦合在一起。受到岩石的挤压或拉伸时,筒内的液体压力发生改变,通过液压的增大或缩小,即可获得岩石的应变状态。此外,仪器还可以记录到清晰的固体潮汐变化和地震面波形态。

|
图 1 台站分布 Fig. 1 Distribution of the stations |
取样的钻孔岩芯位于井下传感器安装段,其中徐州台、邳州台、连云港台和溧阳台的平均取芯深度60 m(表 1),占取样总数的60%;新沂台和六合台平均取芯深度80 m;南通台的取芯深度为160 m,取样深度最深。观测层岩性以砂岩为主,占总数50%,其次是灰岩。制备实验样品时,首先将7个台站的钻孔岩芯(直径为150 mm)制作成2个圆柱体试样。端面在平面磨床上磨平、磨光,使其长度、外表面光洁度、两端面光滑度以及平行度都达到国际岩石力学学会(ISRM) 规定的要求。采用WAW-D1000型电液伺服万能实验系统进行单轴压缩实验,采用荷载速率加载控制,加载速率为0.1 kN/s,持续加载直至试样破坏。整个实验在中国地震局地质研究所地震动力学国家重点实验室完成。
|
|
表 1 仪器基础信息 Tab. 1 The basic information of the instruments |
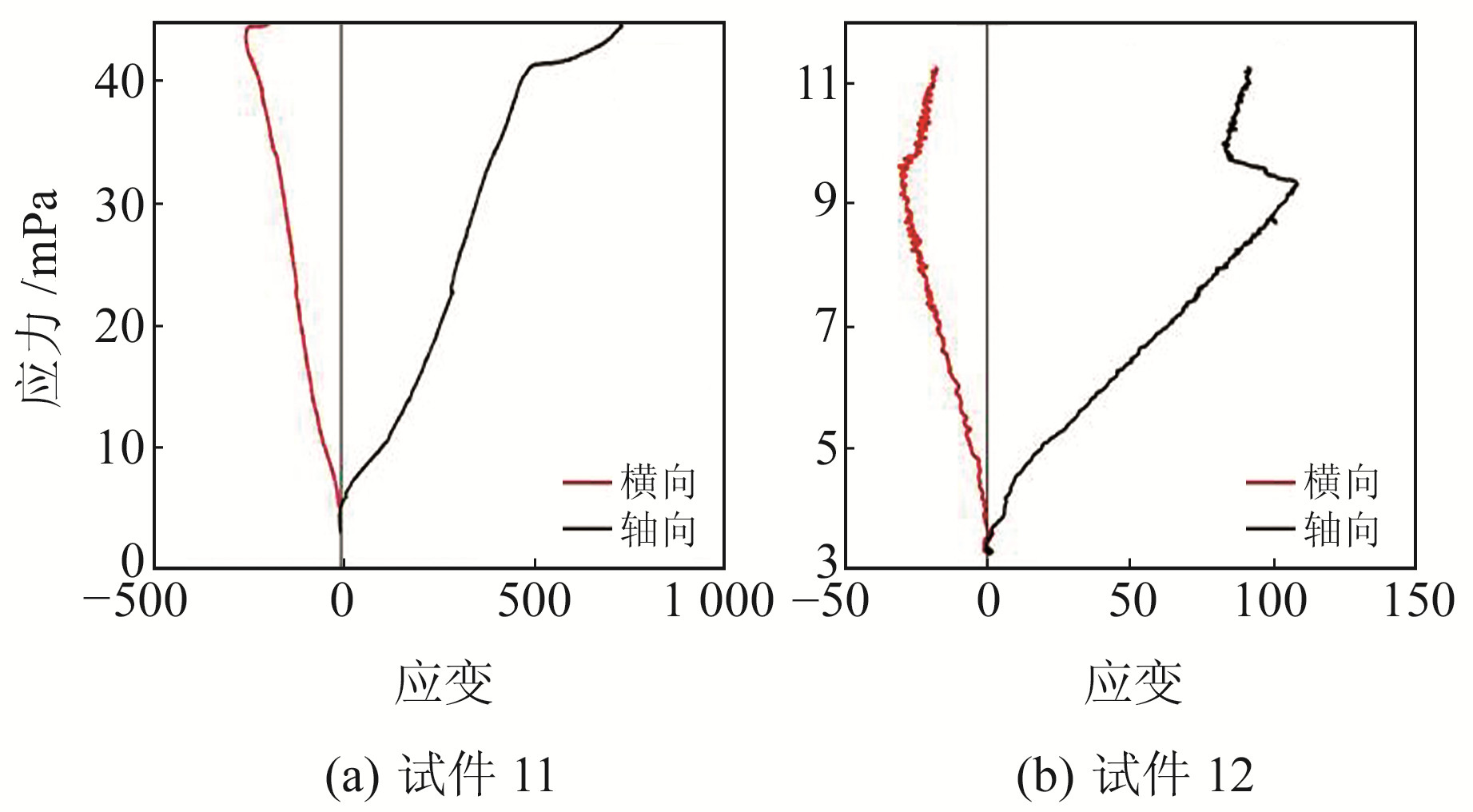
根据单轴压缩条件下岩石试件的应力-应变变化特性,全应力-应变曲线可分为裂纹闭合、线弹性变形、裂纹稳定扩展、裂纹非稳定扩展、峰后破坏5个阶段。本文以分布在茅东断裂带的台站(溧阳台)和郯庐断裂带江苏段的台站(新沂台)为例,分析试件的应力-应变变化特征。因选取的井下传感器安装段岩芯较为致密,在压应力作用下应变量变化微小。尽管2个台站的岩芯均在较短时间内完成了试样的压密阶段,但仍然可以看出新沂台岩芯致密性较溧阳台的差,在压密阶段岩芯的进程出现明显波动(图 2、3)。实验进入到弹性阶段,因为岩石在压密阶段完成了微裂隙的闭合,因此该阶段线性表现均较好。在临近峰值荷载的时候,试样完全破坏,岩石强度不断下降,由于前期宏观破裂面形成,岩石破裂成几块。
|
图 2 单轴压缩条件下溧阳台应力-应变曲线 Fig. 2 Stress-strain curves of Liyang station in uniaxial compression test |

|
图 3 单轴压缩条件下新沂台应力-应变曲线 Fig. 3 Stress-strain curves of Xinyi station in uniaxial compression test |
根据岩芯的应力-应变曲线的斜率可以得到弹性模量:
| $ E=\frac{\sigma}{\varepsilon_a} $ | (1) |
式中,E为岩石弹性模量(单位GPa),σ为应力,εa为应变。
泊松比通过单轴拉伸实验获得:
| $ \nu=\frac{\varepsilon_b}{\varepsilon_a} $ | (2) |
式中,ν为岩石泊松比,εb为应力-应变曲线弹性段横向应变,εa为应力-应变曲线弹性段纵向应变。
通过单轴压缩实验,获得各试样的力学参数,见表 2。
|
|
表 2 各台试件力学参数计算结果 Tab. 2 Calculation results of mechanical parameters of samples at each station |
为了研究单轴压缩条件下不同台站的岩芯试件物理力学参数特征,对实验过程中的相关数据(表 1)进行统计分析可知,同一钻孔内2个岩石样品具有大致相同的矿物颗粒和结构,在宏观上具有一致性,测试曲线具有显著的线弹性特征,但岩石材料本身具有非均质性,局部结构不同,使得测试结果存在差异。由于岩石弹性模量受应力环境的影响是一个动态模量,本文取2个样品的测试平均值。
2 面应变耦合系数的计算使用三层复合双衬结构模型[1-2]计算面应变的理论耦合系数,使用理论固体潮标定法[4]计算面应变的实测耦合系数。
2.1 三层复合双衬结构模型设钢筒、水泥、岩石的弹性模量和泊松比分别为E1和μ1、E2和μ2、E3和μ3。假定采样岩芯介质均为各向同性弹性体,忽略井口及井底对传感器的影响,钻孔的轴向应力σ3=0。面应变的表达式为:
| $ \varepsilon_{m i}=\frac{2 k\left(\sigma_1+\sigma_2\right)}{E_3} $ | (3) |
k值的计算参考张凌空等[7]的双衬套法:
| $ k=\frac{E_3 x_4}{E_1} $ | (4) |
| $ x_4=\frac{r_2^2 r_3^2\left(\alpha_2+\beta_2\right)\left(\alpha_3+\beta_3\right)}{r_2^2\left(\alpha_2-\alpha_3\right)\left[r_1^2\left(\alpha_1+\beta_2\right)+r_2^2\left(\beta_1-\beta_2\right)\right]+r_3^2\left(\alpha_3+\beta_3\right)\left[r_1^2\left(\alpha_1-\alpha_2\right)+r_2^2\left(\alpha_2+\beta_2\right)\right]} $ | (5) |
式中,α1=(1+μ1)E1,α2=(1+μ2)/E2,α3=(1+μ3)E3,β1=(1-μ1)/E1,β2=(1-μ2)/E2,β3=(1-μ3)E3,r1、r2分别为钢筒内、外半径,r3为井孔半径。
平面应力作用下,面应变观测理论耦合系数计算公式为:
| $ \beta_m=\frac{2 k}{1-\mu_3} $ | (6) |
在面应变耦合系数的求解式(6)中,需要知道体应变仪地下传感器安装位置岩芯段的弹性模量和泊松比。根据TJ-2体应变仪技术参数可知,E1=21×1010 Pa,μ1=0.30,E2=3.0×1010 Pa,μ2=0.25,r1=42 mm,r2=44.5 mm和r3=65 mm,E3和μ3根据单轴压缩实验获取。各台站面应变理论耦合系数βm计算结果见表 3。
|
|
表 3 各台站的面应变理论耦合系数 Tab. 3 Theoretical coupling coefficient of surface strain at each station |
体应变的观测对象是“体积”的相对变化,地下传感器的长度比截面直径大很多,轴向线应变要比径向的小得多,并且观测层一般在60 m左右,接近地表轴向应力分量σ3=0,体应变观测值S可以表述为[4]:
| $ S=A\left(\varepsilon_x+\varepsilon_y\right)=A\left(\varepsilon_1+\varepsilon_2\right) $ | (7) |
式中,A为面应变实测耦合系数,εx、εy为钻孔体应变仪在水平方向2个分量的观测值。
采用球状径向不均匀弹性地球模型[3]计算理论面应变,考虑太阳和月亮万有引力变化的影响,忽略海潮、地质构造等因素的影响。设θ和λ分别为地面上一点的余纬和东经,R为地球半径,g0为地球平均重力加速度,n阶起潮力在地球表面上一点p某一时刻产生的水平方向固体潮理论应变为:
| $ \varepsilon_{\theta \theta}=\frac{1}{R g_0}\left(h_n W_n+l_n \frac{\partial^2 W_n}{\partial \theta^2}\right) $ | (8) |
| $ \varepsilon_{\lambda\lambda}=\frac{1}{R g_0}\left(h_n W_n+l_n \cot \theta \frac{\partial W_n}{\partial \theta}+\frac{l_n}{\sin ^2 \theta} \frac{\partial^2 W_n}{\partial \lambda^2}\right) $ | (9) |
| $ \varepsilon_{\lambda \theta}=\frac{1}{R g_0 \sin \theta}\left(\frac{\partial^2 W_n}{\partial \theta \partial \lambda}-\cot \theta \frac{\partial W_n}{\partial \lambda}\right) $ | (10) |
式中,hn和ln为勒夫数,hn等于球状径向不均匀弹性地球模型表面在n阶起潮力作用下的垂直位移与平衡潮潮高的比值,ln等于水平位移与平衡潮水平位移的比值,Wn为月亮和地球在地球内部任意一点p的起潮力位,可以近似表示为:
| $ W_n=W_{m 2}+W_{m 3}+W_{s 2} $ | (11) |
式中,Wm2、Wm2和Ws2分别为月亮的二阶、三阶起潮力位和太阳的二阶起潮力位。
本文使用邱泽华等[4]的理论应变固体潮程序,通过拟合观测值与理论值的小时差分曲线方法进行实地标定求解A,计算结果见表 4。
|
|
表 4 根据观测值计算的面应变实测耦合系数 Tab. 4 The measured coupling coefficient of surface strain calculated from the observed values |
由表 4可见,实测耦合系数A随时间变化,总体接近0.45;新沂台和邳州台实测耦合系数A明显偏小,邳州台还存在比较明显的波动,这2个台站的井下传感器耦合可能存在一定问题。
3 面应变耦合系数相关性与观测精度理论耦合系数βm和实测耦合系数A存在如下关系[7]:
| $ \beta_m=2 A $ | (12) |
采用式(12),将各个台站体应变仪的理论耦合系数和实测耦合系数代换后,不同方法计算的耦合系数的相关性见图 4。可以看出,各个台站实测的面应变耦合系数普遍小于理论耦合系数。实测耦合系数和理论耦合系数符合比较好的有连云港台、南通台、溧阳台和徐州台,2种系数差值小于0.1。其中,徐州台的实测耦合系数和理论耦合系数最为接近,两者仅相差0.016 3。实测耦合系数和理论耦合系数符合较差的有新沂台、邳州台和六合台,2种系数差值大于0.1。其中,新沂台和邳州台的理论耦合系数大于实测耦合系数,六合台的实测耦合系数大于理论耦合系数。

|
图 4 各台站面应变耦合系数与观测精度 Fig. 4 Surface strain coupling coefficient and observation accuracy of each station |
为了进一步定量评价各台站应变仪面应变耦合系数,基于应变仪器可以记录到清晰的固体潮汐变化,采用固体潮汐变化M2波的潮汐因子相对中误差的比值作为评价体应变观测数据质量的指标,比值越小,说明仪器的观测精度越高、在固体潮频段数据质量越高。采用Venedikow调和分析方法计算每个台站相对应时间段内观测精度的均值,结果见图 4。可以看出,观测精度与面应变理论耦合系数和实测耦合系数呈正相关的关系。面应变理论耦合系数和实测耦合系数一致性越好,观测精度越高(相对误差比值越小)。其中,徐州台、溧阳台、连云港台和南通台面应变耦合系数理论值与实测值的差值较小,相对应台站的观测精度较高。新沂台、邳州台和六合台的观测精度分别为0.021 9、0.043 8和0.014 4,均超过0.01,相应的面应变耦合系数理论值和实测值的差异也较大。
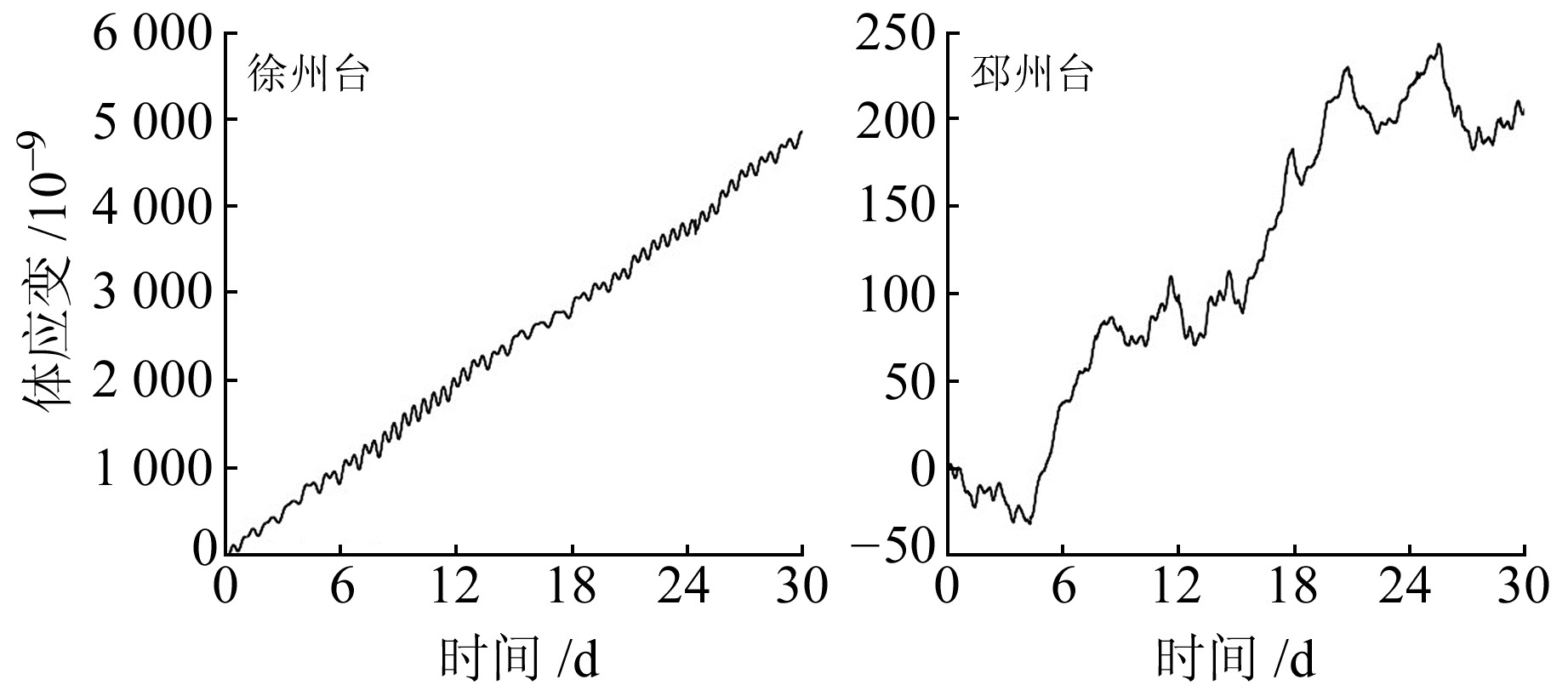
观测精度可以直观评价观测数据的质量,观测数据质量也反映了传感器与井孔的耦合情况。图 5给出观测精度最高的徐州台和观测精度最低的邳州台的原始观测数据。可以看出,徐州台的观测曲线动态变化背景清晰,能清楚地记录到正常的固体潮汐变化,相应的观测精度较高;邳州台日常观测固体潮汐形态较差,面应变耦合系数理论值和实测值相差最大,相应的观测精度较差,可能这个台站的井下传感器存在一定的耦合问题,直接导致观测数据的精度不高。
|
图 5 徐州台和邳州台2020-03-01~31原始观测曲线 Fig. 5 Original observation curve at Xuzhou and Pizhou stations from March 1 to 31, 2020 |
1) 井下传感器与围岩的耦合程度,是钻孔体应变观测效能的主要影响因素。体应变钻孔岩芯的弹性参数是非常重要的基础数据,通过单轴压缩实验获取相关的弹性模量和泊松比,结合观测模型、系统各组成部分的几何参数获得较为合理的面应变耦合系数。从计算结果来看,江苏区域内整体的面应变理论耦合系数在0.9左右(表 3)。
2) 徐州台、连云港台、南通台和溧阳台的面应变耦合系数理论值和实测值的差值均小于0.1,说明这4个台站的钻孔安装条件和场地条件较好,井下传感器与围岩耦合理想。新沂台和邳州台的面应变耦合系数理论值和实测值的差值均在0.5左右,可能存在井下耦合问题。
3) 钻孔应变仪的观测精度与理论耦合系数和实测耦合系数呈正相关,钻孔应变仪器的理论耦合系数和实测耦合系数一致性越好,仪器的观测精度越高、数据质量越好。江苏省各台站面应变理论耦合系数和实测耦合系数差值的阈值为0.1,当理论耦合系数和实测耦合系数差值小于0.1,说明观测数据质量较高;差值在0.1~0.2之间,说明井下耦合对观测精度有一定影响,但是不显著;当差值超过0.2,说明井下耦合存在问题,仪器的观测精度较低、数据的观测质量较差。
| [1] |
张凌空, 牛安福. 钻孔体应变与面应变观测井孔耦合系数的计算[J]. 地震学报, 2015, 37(1): 80-88 (Zhang Lingkong, Niu Anfu. Calculation of Borehole Coupling Coefficient Based on Borehole Volume Strain and Area Strain Observation[J]. Acta Seismologica Sinica, 2015, 37(1): 80-88)
(  0) 0) |
| [2] |
张凌空, 牛安福. 基于双衬套理论求解地壳岩石应变传递系数的探讨[J]. 地球物理学进展, 2017, 32(4): 1 525-1 531 (Zhang Lingkong, Niu Anfu. Discussion on Solution of Crustal Rock Strain Transfer Coefficient Based on Double Bush Theory[J]. Progress in Geophysics, 2017, 32(4): 1 525-1 531)
(  0) 0) |
| [3] |
吴庆鹏. 重力学与固体潮[M]. 北京: 地震出版社, 1997 (Wu Qingpeng. Gravity and Solid Tide[M]. Beijing: Seismological Press, 1997)
(  0) 0) |
| [4] |
邱泽华, 石耀霖, 欧阳祖熙. 四分量钻孔应变观测的实地相对标定[J]. 大地测量与地球动力学, 2005, 25(1): 118-122 (Qiu Zehua, Shi Yaolin, Ouyang Zuxi. Relative In-Situ Calibration of 4-Component Borehole Strain Observation[J]. Journal of Geodesy and Geodynamics, 2005, 25(1): 118-122)
(  0) 0) |
| [5] |
何斌, 江昊琳, 章东, 等. 基于单轴压缩实验的钻孔应变仪岩芯力学性质的研究[J]. 地震学报, 2020, 42(6): 697-706 (He Bin, Jiang Haolin, Zhang Dong, et al. Study on the Mechanical Properties of Core about Borehole Strain Meters Based on Uniaxial Compression Experiment[J]. Acta Seismologica Sinica, 2020, 42(6): 697-706)
(  0) 0) |
| [6] |
何斌, 田韬, 王恒知. 基于钻孔特性的体应变观测相关性研究[J]. 地震工程学报, 2018, 40(1): 153-158 (He Bin, Tian Tao, Wang Hengzhi. Study on Correlation of Volume Strain Observation Based on Borehole Features[J]. China Earthquake Engineering Journal, 2018, 40(1): 153-158)
(  0) 0) |
| [7] |
张凌空, 牛安福. 钻孔体应变与面应变观测参数k的计算[J]. 中国地震, 2013, 29(3): 335-346 (Zhang Lingkong, Niu Anfu. Calculation of Borehole Volumetric Strain and Area Strain Observation Parameter k[J]. Earthquake Research in China, 2013, 29(3): 335-346)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43

