2. 山东五征集团有限公司,山东省日照市莲海大道9号,262300;
3. 航天器在轨故障诊断与维修重点实验室,西安市咸宁东路462号,710043
地心运动的研究分析是构建mm级地球参考框架的关键步骤之一,对空间大地测量和地球物理学研究具有重大意义。由于受到空间大地测量技术误差和数据处理策略的影响,解算得到的地心运动序列存在噪声,因此需要对地心运动序列进行降噪处理。地心运动序列中的噪声可以分为白噪声(white noise, WN)和有色噪声,其中有色噪声分为幂律噪声(power-law noise, PL)、闪烁噪声(flicker noise, FN)、一阶自回归噪声和广义高斯马尔科夫噪声等[1-2]。目前用于地心运动序列降噪的方法主要有多通道奇异谱分析法、小波分解法、变分模态分解法等[3-5]。与小波分解法相比,LOESS方法的降噪性能更优[6]。陈祥等[7]将LOESS方法用于全球导航卫星系统GNSS的垂向坐标时间序列降噪分析中,效果较好。
本文将LOESS方法引入地心运动时序的降噪分析中,通过样本点与拟合点之间的距离自动确定局部权重,从而使得模型对复杂时间序列具有更强的滤波能力和自适应性。但LOESS方法仅考虑数据在自变量方向上分布的不均匀性,而没有考虑数据在因变量方向上波动特征的非齐性[8]。基于此,本文提出一种结合LOESS和EMD的LOESS-EMD降噪方法,对仿真数据和IGS Repro3提供的地心运动数据进行降噪研究,验证LOESS-EMD方法的优越性。
1 LOESS-EMD降噪方法 1.1 局部加权回归法LOESS是一种基于局部拟合的非参数回归方法[9],对具有复杂波动性的数据进行平滑处理时效果较好。该方法首先需要预设一个带宽因子,根据总样本数和带宽因子计算局部拟合的窗口长度,然后对带宽中的样本进行加权最小二乘拟合计算。权重由样本点到拟合点在自变量方向上的距离确定,距离越近,可靠性越高,权重越大。从左到右依次对原始序列中的点进行拟合,最后把拟合点连接在一起,即为LOESS回归曲线。设(xi,yi)(i=1, 2, 3, …,n)为原始序列,LOESS具体过程如下:
1) 设定带宽因子f,计算窗口长度,确定每次参与拟合的样本数,k取最接近的正整数。
2) 确定X方向上最接近拟合点(x,y)的k个点(xi,yi)(i=1, 2, 3, …,k),对各样本点与拟合点在X方向上的距离进行归一化处理,并采用三次权重函数进行转化:
| $ u\left(x_i\right)=\frac{\left|x-x_i\right|}{\Delta(x)} $ | (1) |
| $ W(u)=\left\{\begin{array}{l} \left(1-u^3\right)^3, 0 \leqslant u<1 \\ 0, u \geqslant 1 \end{array}\right. $ | (2) |
式中,u(xi)为样本点与拟合点在X方向上的归一化距离,Δ(x)为最远的样本点与拟合点在X方向上的距离,W(u)为三次权重函数。由此计算各样本点的权重为:
| $ v\left(x_i\right)=W\left(\frac{\left|x-x_i\right|}{\Delta(x)}\right) $ | (3) |
式中,v(xi)为点(xi,yi)相对于点(x,y)的权重。样本点靠近拟合点处的权重趋近于1,递减到最远处权重为0。
3) 令局部加权回归的损失函数J(β)最小,求得最佳回归系数β 和拟合点(x,
| $ J(\beta)=\frac{1}{k} \sum\limits_{i=1}^k\left(y_i-\boldsymbol{\beta}^{\mathrm{T}} x_i\right)^2 v\left(x_i\right) $ | (4) |
4) 重复上述步骤,对原始序列中所有点进行拟合,得到LOESS回归曲线。
1.2 经验模态分解EMD是一种处理非线性非平稳信号的信号分解方法[10],该方法可以自适应地将复杂信号从高频到低频依次分解为多个内涵模态函数IMF和一个趋势分量,其表达式为:
| $ x(t)=\sum\limits_{i=1}^n c_i(t)+r_n(t) $ | (5) |
式中,x(t)为原始信号,rn(t)为趋势项,ci(t)为频率从高到低依次排列的IMF分量。每个IMF分量必须满足以下2个条件:1)在整个序列中,零点与极值点的数目至多相差一个;2)任意一点上,由局部极小值点构成的下包络线和局部极大值点构成的上包络线的局部算数平均值为0[11]。
将原始信号进行EMD处理后分解为n个IMF分量,计算原始信号与n个IMF分量之间的相关系数。认为相关系数序列中第一个取局部极小值的相关系数对应的IMF分量和该分量之前的IMF分量是高频噪声,将剩余IMF分量进行重构,即可得到去噪信号。
1.3 LOESS-EMD方法的降噪流程LOESS方法在对数据进行局部拟合时,可以根据数据在自变量方向上的分布自动调整局部权重,达到数据平滑的目的。但当拟合点附近存在偏差较大的点时,按照距离越近、权重越大的原则得到的拟合效果较差。因此,本文引入EMD分解对LOESS方法进行改良,使最终的拟合结果更接近真实值。
LOESS-EMD方法对地心运动序列进行降噪分析的具体流程如下:
1) 采用四分位距法剔除地心运动序列中的粗差,并采用三次样条插值法补全缺失值;
2) 采用LOESS方法对原始时间序列进行拟合,得到拟合值和残差序列;
3) 对残差进行EMD分解,采用相关系数法筛选并重构分解得到的多个IMF分量,得到其中的低频信号,其他高频部分为需要剔除的噪声项;
4) 将拟合值和残差中低频部分进行重构,得到降噪后的时间序列;
5) 综合数学指标对降噪效果进行评价。
2 仿真实验分析根据文献[12]的结果,本文利用4个主要周期的振幅和相位生成地心运动序列的真值,并添加信噪比为5的噪声(WN和PL分别为70%和30%)作为仿真数据,验证LOESS-EMD方法的性能。4个周期函数和纯净信号的公式为:
| $ \left\{\begin{array}{l} y_1(t)=2.07 \cos \left(\frac{2 \pi t}{365}-11.78\right), \\ y_2(t)=1.28 \cos \left(\frac{2 \pi t}{4000}+48.73\right), \\ y_3(t)=0.71 \cos \left(\frac{2 \pi t}{1334}+79.50\right), \\ y_4(t)=0.46 \cos \left(\frac{2 \pi t}{182}-50.94\right), \end{array} t \in[1, 4018]\right. $ | (6) |
| $ x(t)=y_1(t)+y_2(t)+y_3(t)+y_4(t) $ | (7) |
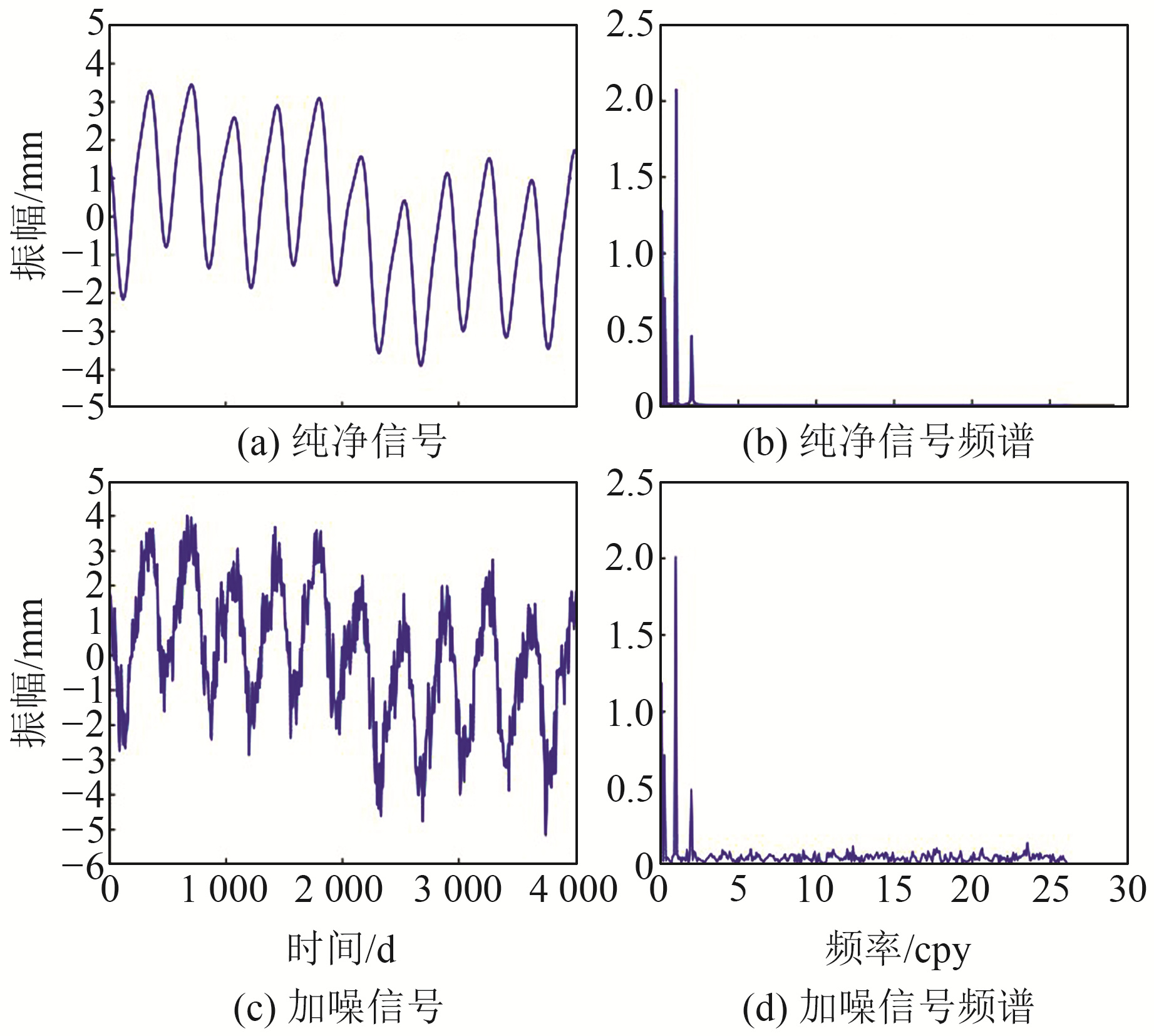
式中,x(t)为纯净信号;y1(t)、y2(t)、y3(t)、y4(t)分别为4个周期函数,代表地心运动的4个主要周期项。图 1为纯净信号、加噪信号及其频谱图,采样间隔为7d。
|
图 1 纯净信号、加噪信号及其频谱 Fig. 1 Pure and noised signals and their spectrograms |
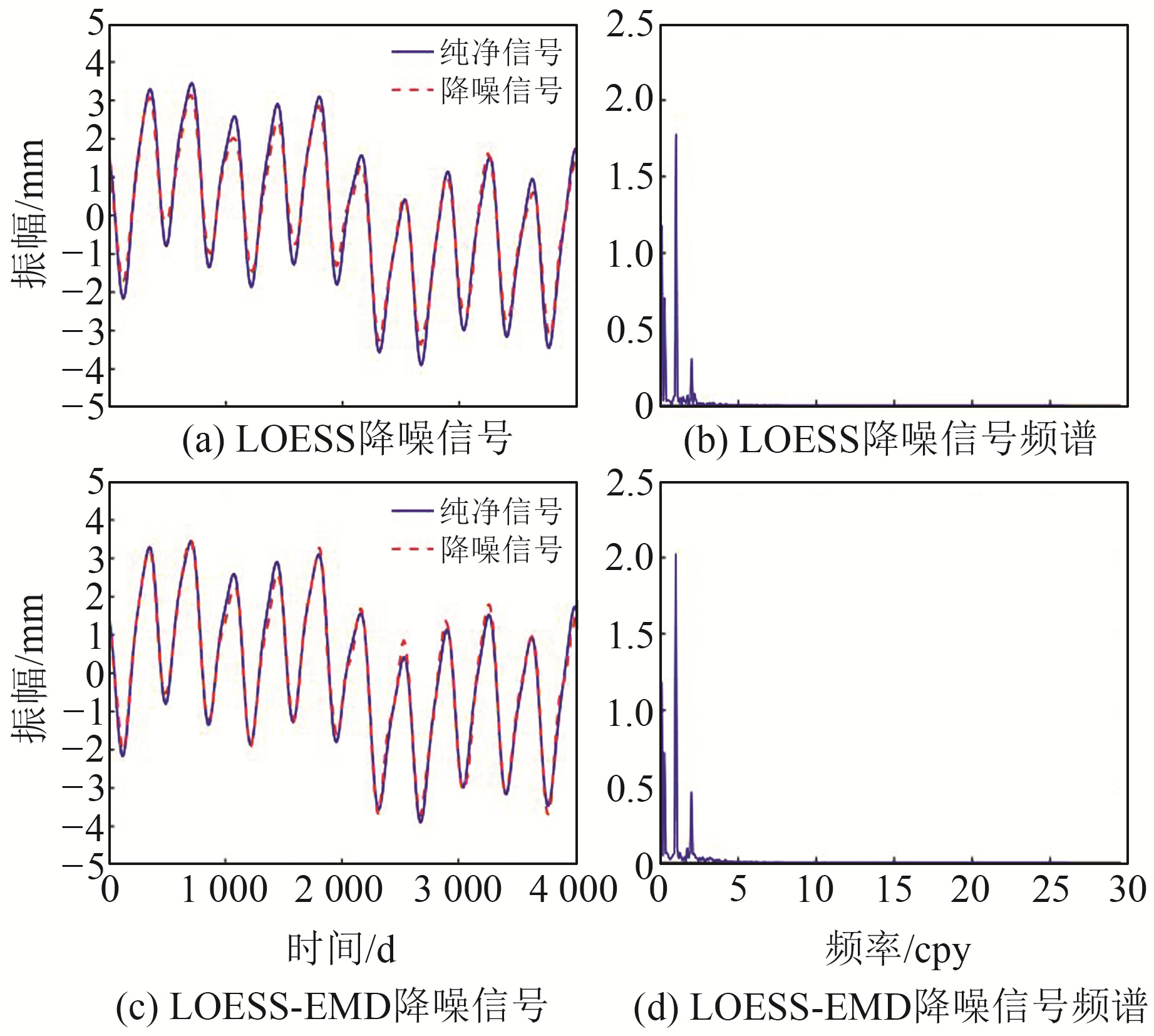
分别利用LOESS-EMD方法和LOESS方法对仿真数据进行降噪分析,将降噪信号直接与真值进行对比。2种方法得到的降噪信号及其频谱如图 2所示。
|
图 2 仿真实验降噪效果及频谱 Fig. 2 Simulation experiment noise reduction effect and spectrogram |
由图 2(a)、(c)可见,2种方法均能去除原始信号中的大部分噪声。LOESS方法的降噪信号在一定程度上偏离了纯净信号,出现降噪过度的现象;LOESS-EMD方法的降噪信号更接近于纯净信号,降噪效果更好。由图 2(b)、(d)可见,LOESS方法降噪信号频谱中1 cpy(对应年周期)处的峰值比原始信号对应峰值减小约0.28 mm,LOESS-EMD方法降噪信号频谱中对应峰值并未明显减小,说明LOESS-EMD方法在剔除噪声成分的同时并未损失有效信息。
为定量分析LOESS-EMD方法与LOESS方法的降噪效果,采用均方根误差RRMSE、信噪比SSNR、剩余能量百分比EESN3种评价指标分别对以上2种方法的降噪效果进行评估。其中,RRMSE表示降噪信号和原始信号之间的拟合程度,RRMSE越小,说明降噪信号越接近原始信号;SSNR表示原始信号和噪声成分的比值,SSNR越大,说明降噪效果越好;EESN为降噪信号占原始信号的能量百分比,EESN越大,说明降噪信号越能保持原始信号特征。仿真实验评价指标的统计结果见表 1。
|
|
表 1 仿真实验评价指标 Tab. 1 Simulation experiment evaluation index |
由表 1可知,相较于LOESS方法,LOESS-EMD方法的均方根误差减小31%,说明LOESS-EMD方法降噪后的地心运动序列更接近于真值;信噪比和剩余能量百分比分别提高16%和0.16百分点,说明LOESS-EMD方法的降噪效果更优。
3 实测数据应用 3.1 地心运动数据及预处理为验证LOESS-EMD方法的实用性,分别采用LOESS-EMD方法和LOESS方法对IGSRepro3提供的地心运动数据进行降噪对比分析。IGS利用最新误差改正模型和数据处理策略,重新分析1994~2020年的GNSS数据,并运用网平移法得到地心运动序列。由于早期的GNSS数据质量较差,在此基础上解算的地心运动序列误差过大,因此本文选取2010~2020年IGS Repro3提供的地心运动数据,采样间隔为7 d。
对地心运动序列进行降噪之前先进行预处理,以消除原始时间序列中粗差带来的影响。首先采用四分位距法(inter quartile range, IQR)对原始时间序列进行粗差探测与剔除,然后用三次样条插值法补全缺失值。
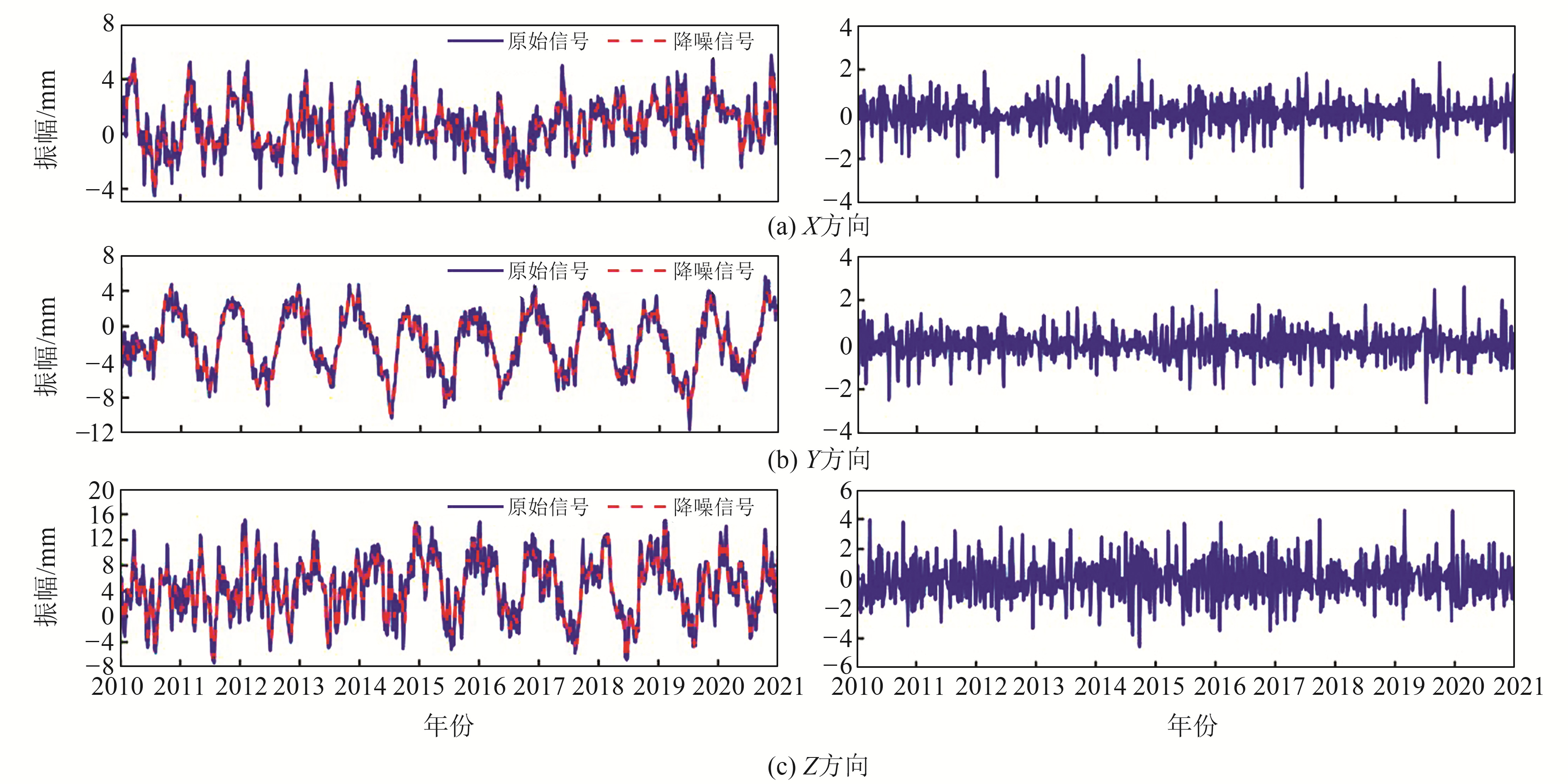
3.2 地心运动数据降噪分析采用LOESS-EMD方法对选取的数据进行降噪分析,X、Y、Z三个方向上的降噪效果如图 3(右图为残差项)所示。由图可见,降噪信号与原始信号的走势基本相同,说明降噪信号保留了原始信号的大部分有效信息,有利于地心运动序列的分析。而分离出的残差项振幅较小,大部分在2 mm以内波动,无明显周期特征,将其剔除能够提高地心运动序列的精度。
|
图 3 地心运动序列降噪效果 Fig. 3 Geocentric motion sequence noise reduction results |
由于无法获取地心运动的真值,在实测数据实验中均方根误差和剩余能量百分比等指标不再适用,因此本文将地心运动序列和残差序列与时间的最大互信息系数(maximal information coefficient, MIC)作为实测数据降噪效果的评价指标。MIC是衡量2个变量之间相关性的指标,具有普适性、公平性、标准化以及鲁棒性,在样本充足时能捕获各种相关关系。MIC值为0~1,值越大表示相关性越强,反之则表示相关性越弱[13]。
地心运动序列中所包含的有一定变化规律的非线性成分与时间的相关性较强,而噪声成分与时间的相关性较弱。可以将MIC值作为实测数据降噪效果的评价指标,降噪后地心运动序列与时间的MIC值越大,表示该序列中保留的有效信息越多;MIC值越小,表示该序列中噪声成分越高。实测数据评价指标统计结果见表 2。
|
|
表 2 实测数据评价指标 Tab. 2 Measured data evaluation index |
由表 2可知,LOESS-EMD方法降噪后残差序列的MIC值约为0.1,具有弱时间相关性,说明残差序列中绝大部分为需要剔除的噪声。与LOESS方法相比,LOESS-EMD方法对3个方向进行降噪处理后地心运动序列的MIC值分别增大0.136、0.105和0.134,即分别提高17%、12%、17%;残差序列的MIC值分别减小0.054、0.033和0.045,即分别减小33%、26%和27%。通过上述MIC值的变化可知,LOESS-EMD方法在保证降噪后地心运动序列强时间相关性的同时,也能保证残差序列的弱时间相关性,原始地心运动序列在经过LOESS -EMD方法降噪后精度更高,该方法的降噪效果相对于LOESS方法有较大提升。
4 结语1) 在仿真数据实验中,相对于LOESS方法,LOESS-EMD方法降噪结果的均方根误差减小31%,信噪比和剩余能量百分比分别提高16%和0.16百分点。实验结果表明,LOESS方法存在降噪过度的问题,而LOESS-EMD方法可以剔除大部分噪声且降噪信号更接近纯净信号。
2) 在实测数据实验中,相对于LOESS方法,LOESS-EMD方法对3个方向进行降噪处理后地心运动序列的MIC值分别提高17%、12%、17%,残差序列的MIC值分别减小33%、26%和27%,分离出的残差序列绝大部分为需要剔除的噪声。结果表明,LOESS-EMD方法在剔除复杂噪声的同时能保留大部分有效信息,对地心运动序列有较好的降噪效果。实验数据定量验证了该方法的可行性和有效性,证明LOESS-EMD方法可用于地心运动序列的降噪研究中。
| [1] |
Ma Y F, Rebischung P, Altamimi Z, et al. Assessment of Geocenter Motion Estimates from the IGS Second Reprocessing[J]. GPS Solutions, 2020, 24(2): 55 DOI:10.1007/s10291-020-0968-2
(  0) 0) |
| [2] |
Zhang X, Jin S. Uncertainties andEffects on Geocenter Motion Estimates from Global GPS Observations[J]. Advances in Space Research, 2014, 54(1): 59-71 DOI:10.1016/j.asr.2014.03.021
(  0) 0) |
| [3] |
Jin X, Liu X, Guo J Y, et al. Multi-Channel Singular Spectrum Analysis on Geocenter Motion and Its Precise Prediction[J]. Sensors(Basel, Switzerland), 2021, 21(4): 1 403 DOI:10.3390/s21041403
(  0) 0) |
| [4] |
郭金运, 常晓涛, 韩延本, 等. 由SLR观测的地心周期性运动(1993~2006年)[J]. 测绘学报, 2009, 38(4): 311-317 (Guo Jinyun, Chang Xiaotao, Han Yanben, et al. Periodic Geocenter Motion Measured with SLR in 1993-2006[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 311-317 DOI:10.3321/j.issn:1001-1595.2009.04.005)
(  0) 0) |
| [5] |
王庆余, 杜宁, 王莉, 等. 变分模态分解及能量熵在地心运动降噪中的应用[J]. 测绘通报, 2020(8): 59-64 (Wang Qingyu, Du Ning, Wang Li, et al. Application of Variational Mode Decomposition and Energy Entropy in Denoising of Geocentric Motion[J]. Bulletin of Surveying and Mapping, 2020(8): 59-64)
(  0) 0) |
| [6] |
Moosavi S R, Qajar J, Riazi M. A Comparison of Methods for Denoising of Well Test Pressure Data[J]. Journal of Petroleum Exploration and Production Technology, 2018, 8(4): 1 519-1 534 DOI:10.1007/s13202-017-0427-y
(  0) 0) |
| [7] |
陈祥, 杨志强, 杨兵, 等. LOESS用于GNSS垂向坐标时间序列噪声识别与提取[J]. 大地测量与地球动力学, 2021, 41(10): 1 024-1 029 (Chen Xiang, Yang Zhiqiang, Yang Bing, et al. Noise Recognition and Extraction of GNSS Vertical Coordinate Time Series Based on LOESS[J]. Journal of Geodesy and Geodynamics, 2021, 41(10): 1 024-1 029 DOI:10.14075/j.jgg.2021.10.007)
(  0) 0) |
| [8] |
何云飞, 杨联强. 基于局部权重调节的自适应LOESS方法[J]. 统计与决策, 2019, 35(1): 10-14 (He Yunfei, Yang Lianqiang. Adaptive LOESS Method Based on Local Weight Adjustment[J]. Statistics and Decision, 2019, 35(1): 10-14)
(  0) 0) |
| [9] |
Cleveland W S, Devlin S J. Locally Weighted Regression: An Approach to Regression Analysis by Local Fitting[J]. Journal of the American Statistical Association, 1988, 83(403): 596-610 DOI:10.1080/01621459.1988.10478639
(  0) 0) |
| [10] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995 DOI:10.1098/rspa.1998.0193
(  0) 0) |
| [11] |
王笑蕾, 张勤, 张双成. 基于EMD和WD联合算法的GPS水汽时间序列的周期性振荡分析[J]. 武汉大学学报: 信息科学版, 2018, 43(4): 620-628 (Wang Xiaolei, Zhang Qin, Zhang Shuangcheng. Periodic Oscillation Analysis of GPS Water Vapor Time Series Using Combined Algorithm Based on EMD and WD[J]. Geomatics and Information Science of Wuhan University, 2018, 43(4): 620-628)
(  0) 0) |
| [12] |
乔灵娜, 赵春梅, 马天明. 基于EMD方法的地心运动时间序列分析[J]. 测绘通报, 2019(2): 6-11 (Qiao Lingna, Zhao Chunmei, Ma Tianming. Time Series Analysis of Geocenter Motion Based on EMD Method[J]. Bulletin of Surveying and Mapping, 2019(2): 6-11)
(  0) 0) |
| [13] |
孟燕霞. 最大信息系数算法研究[D]. 太原: 太原理工大学, 2019 (Meng Yanxia. The Maximal Information Coefficient Algorithm Research[D]. Taiyuan: Taiyuan University of Technology, 2019)
(  0) 0) |
2. Kexue Road, Zhengzhou 450001, China 2 Shandong Wuzheng Group Co Ltd, 9 Lianhai Road, Rizhao 262300, China;
3. Key Laboratory for Fault Diagnosis and Maintenance of Spacecraft in Orbit, 462 East-Xianning Road, Xi'an 710043, China
 2023, Vol. 43
2023, Vol. 43


