海平面变化具有非线性、非平稳性、多时间尺度变化等特性,因而能将非平稳数据平稳化处理,并得到具有物理意义的特征信号的经验模态分解以及各类神经网络,逐渐应用于海平面变化预测。经验模式分解(EMD)是由Huang等[1]提出的一种针对非平稳信号的分析方法,基于瞬时频率,能够将信号分解为若干个本征模态函数(IMF)分量,每个IMF分量表现信号的各局部特征[2]。针对EMD算法分解信号存在模态混叠的问题,引入基于噪声辅助分析的集合经验模态分解(EEMD)[3];针对EEMD的“残余辅助噪声”缺点,引入互补集合经验模态分解方法(CEEMD)[4]。但是这两种算法分解信号得到的本征模态分量中总会残留一定的白噪声,为了解决该问题,TORRES等[5]提出一种改进算法——完全集合经验模态分解(CEEMDAN),有效解决了白噪声从高频到低频的转移传递问题。利用此种分解方法能够较好地解决海平面变化序列的非平稳、非线性问题,提取出海平面变化序列的周期信息。
LSTM(long short term memory networks)是由Hochreiter和Schmidhuber[6]提出的一种循环神经网络(RNN)架构,属于反馈神经网络的范畴。结合CEEMDAN提取海平面变化信息特征的能力与LSTM神经网络的优势,构建一种CEEMDAN与LSTM的组合方法,对提高海平面变化预测精度有着重要意义。
本文将CEEMDAN-LSTM组合方法应用于中国南海海域海平面变化预测分析,对海平面变化周期性规律进行提取,对区域海平面变化预报研究具有借鉴意义。
1 数据来源本文采用的数据资料为法国AVISO(http://www.aviso.oceanobs.com)提供的格网化海平面异常数据(merged sea level anomaly,MSLA),资料经过必要的地球物理改正,包括电离层延迟、对流层干湿分量、固体潮与海潮、海洋负荷潮汐、极潮、电磁偏差、仪器、反变气压计等的改正或校正。本文选取时间分辨率为7 d、空间分辨率为0.25°×0.25°、时间跨度为1993~2016年的南海海域格网SLA数据作为研究对象,对该海域格网数据进行分析。
2 CEEMDAN与LSTM方法 2.1 CEEMDAN方法CEEEMDAN方法是TORRES等[5]提出的一种分解方式。构建步骤如下:
1) 将待分解信号y(t)添加K次均值为0的高斯白噪声,构造共K次实验的待分解序列, 对上述序列进行EMD分解,得到第1个模态分量(IMF)并取其均值作为CEEMDAN分解得到的第1个IMF。
2) 通过计算去除第1个模态分量后的残差得到r1(t),将分解后得到的r1(t)余量信号添加特定噪声后,继续进行EMD分解,得到第2个本征模态分量C2,消除C2残差。重复上述步骤直到第n次分解的余量信号rn(t)为单调信号,则停止以上步骤[5]。此时得到的本征模态分量数量为K,则原始信号y(t)被分解为:
| $ y(t)=\sum\limits_{k=1}^K C_k(t)+r_k(t) $ | (1) |
Hochreiter等提出一种基于“门”的结构进行记忆的LSTM神经网络模型,增加遗忘、输入和输出3个门限,可避免在预测过程中的梯度消失和梯度爆炸问题。
在t时刻,xt表示为当前时刻的输入数据,ht-1则为上一时刻网络内循环数据,ct-1为上一时刻的网络单元状态,则t时刻的输出数据ht和单元状态ct的计算过程如式(2)~式(4)。其中,W表示权值矩阵,b表示偏移量,σ表示Sigmoid函数,tanh表示tanh函数[6]。
遗忘门的表达式为:
| $ f_t=\sigma\left(\boldsymbol{W}_f \cdot\left[h_{t-1}, x_t\right]+\boldsymbol{b}_f\right) $ | (2) |
前一个时间步的循环核数据ht-1和第t个时间的输入xt拼接,进入Sigmoid激活函数的神经网络层,生成的数据ft作为记忆的衰减系数,定义为0~1之间的数,代表了上一时刻ct-1应该保留的比率。0代表将ct-1数据全部遗忘,1代表将ct-1数据全部保留。
输入门的表达式为:
| $ \left\{\begin{array}{l} i_t=\sigma\left(\boldsymbol{W}_i \cdot\left[h_{t-1}, x_t\right]+\boldsymbol{b}_i\right) \\ c_t=\tanh \left(\boldsymbol{W}_c \cdot\left[h_{t-1}, x_t\right]+\boldsymbol{b}_c\right) \end{array}\right. $ | (3) |
输入门分作两步:第一步,通过Sigmoid层决定网络需要更新的值;第二步,通过Tanh层创建一个新的候选值向量Dt,并将其加入到网络之中[7]。
输出门的表达式为:
| $ \left\{\begin{array}{l} o_t=\sigma\left(\boldsymbol{W}_o \cdot\left[h_{t-1}, x_t\right]+\boldsymbol{b}_o\right) \\ h_t=o_t \cdot \tanh \left(\boldsymbol{D}_t\right) \end{array}\right. $ | (4) |
本文采用时间分辨率为7 d的时间序列进行数据建模,建立LSTM神经网络样本。原始数据共869个周平均海平面数据,被划分为训练样本和测试样本2个部分,其中前695个样本数据(占总样本数据的80%)作为LSTM神经网络训练样本,后174个样本数据(占总样本数据20%)作为测试样本。在输入样本时,为了更好地匹配和防止训练发散,将训练数据标准化为零均值和单位方差,并统一测试数据与训练数据至相同的参数,进行数据的归一化处理。经过反复调试,建立训练样本的预测步长为5,具有128个隐藏单元,其中令10%的神经元处于休眠状态以防止出现过拟合情况,其余参数采用默认参数的LSTM神经网络。完成此模型训练之后,再使用此模型对IMF分量分别进行预测。
3 结果与分析 3.1 海平面变化序列CEEMDAN分解南海海平面异常时间序列经由CEEMDAN分解产生10个IMF分量,分别对应9个周期项和1个长期趋势项,结果如图 1所示。周期项主要包括半月、月、3个月、7个月、13个月、28个月、49个月、100个月。其中第3、第4和第5周期项分别对应季节内变化、半年变化和年变化信号;28个月周期接近于准2 a的大气震荡;49个月周期考虑为3~7 a的ENSO循环,其余周期物理意义尚不明确。
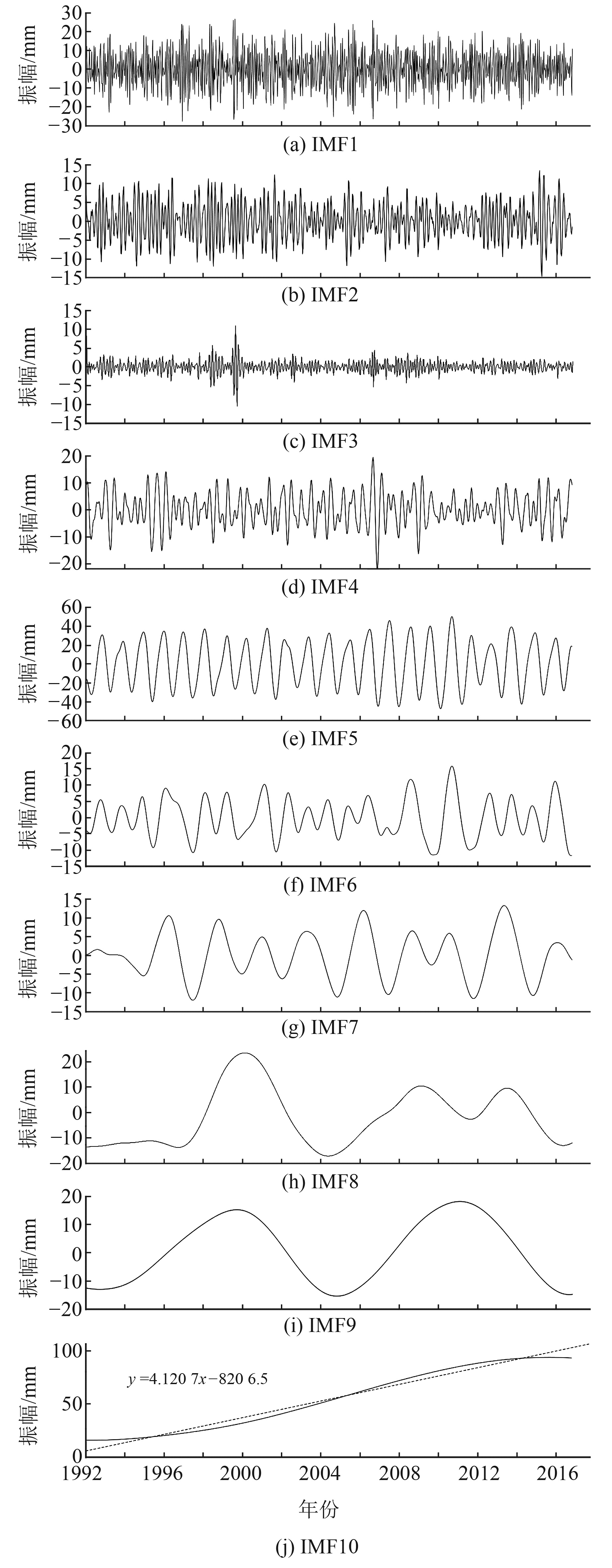
|
图 1 南海海域测高海平面变化数据的CEEMDAN分解结果 Fig. 1 CEEMDAN decomposition results of altimetric sea level change data in the South China Sea |
根据长期趋势项IMF10显示,南海海域1993~2016年海平面变化呈现“上升-下降”的趋势,与潘轶等[8]对1993~2015年中国南海海平面变化的初步研究结果较为一致。拟合结果显示,南海海域1993~2016年海平面变化率为4.12 mm/a,与赵健[9]对中国南海及东海近海测高海平面变化监测与预测结果较为符合。以上结果显示,CEEMDAN能较好地分析基础海平面变化的周期项,提取的长期变化趋势合理。
3.2 CEEMDAN-LSTM组合方法建立CEEEMDAN-LSTM方法预测即先使用CEEEMDAN方法分解数据得到IMF1~10分量,再使用LSTM神经网络分别进行预测。截取预测所得数据与原始IMF数据成图对比如图 2所示。可以看出,类似IMF1(图 2(a))这种高频分量的预测结果较差,但序列整体与样本数据仍较为一致。对于这种情况,推测是因为前期的数据比较复杂,高频、低频信息都存在,且有大量的极值与突变的情况发生,对于这种极值的预测处理,神经网络存在着较大的不足。观察IMF2~10可见,IMF分量逐渐变得平稳,LSTM网络的预测能力显著变好,与样本值达到了高度重合。说明神经网络模型虽然在非平稳、非线性的高频信号处理中有着精度不高的问题,但是随着数据序列趋向平稳,LSTM神经网络的预测精度也随之上升。由于海平面变化是一个较大尺度和大周期的变化,且南海海平面变化主要由年信号组成,所以短期的高频预测效果对大周期的海平面变化影响并不大。
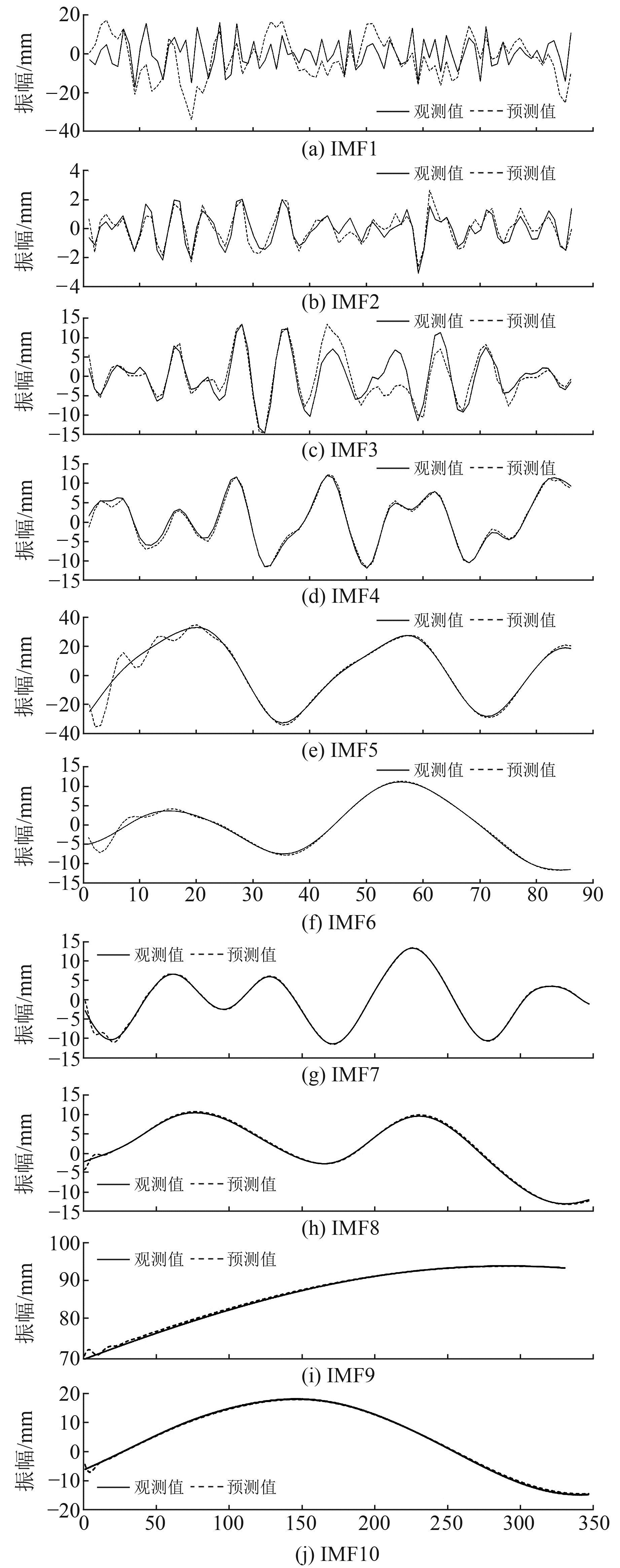
|
图 2 CEEMDAN分解各IMF分量预测值与原始数据对比 Fig. 2 CEEMDAN decomposition of the predicted values of each IMF component compared with the original data |
为了全面体现CEEEMD-LSTM组合方法的预测精度及其与单纯的LSTM网络模型的不同,同时采用直接使用LSTM网络进行预测所得到的结果进行对比,此种预测方法的输入数据为未经过CEEEMDAN分解的原始南海海平面异常时间序列。CEEEMDAN-LSTM组合方法的结果则是由各IMF分量通过LSTM神经网络预测所得值的重构结果。所得成果如图 3所示,可以看出,在大趋势上两种预测方式和原始数据保持着一致,但LSTM神经网络预测在部分极值和突变处出现了较大偏差,而CEEEMDAN-LSTM组合方法预测更贴近原始数据。观察得知,LSTM网络预测容易在原始数据出现极值点和突变处出现误差,这是由于海平面变化是一个大范围的多变性数据,LSTM网络虽然进行了大量的学习,但仍无法预测到各种极值和突变。
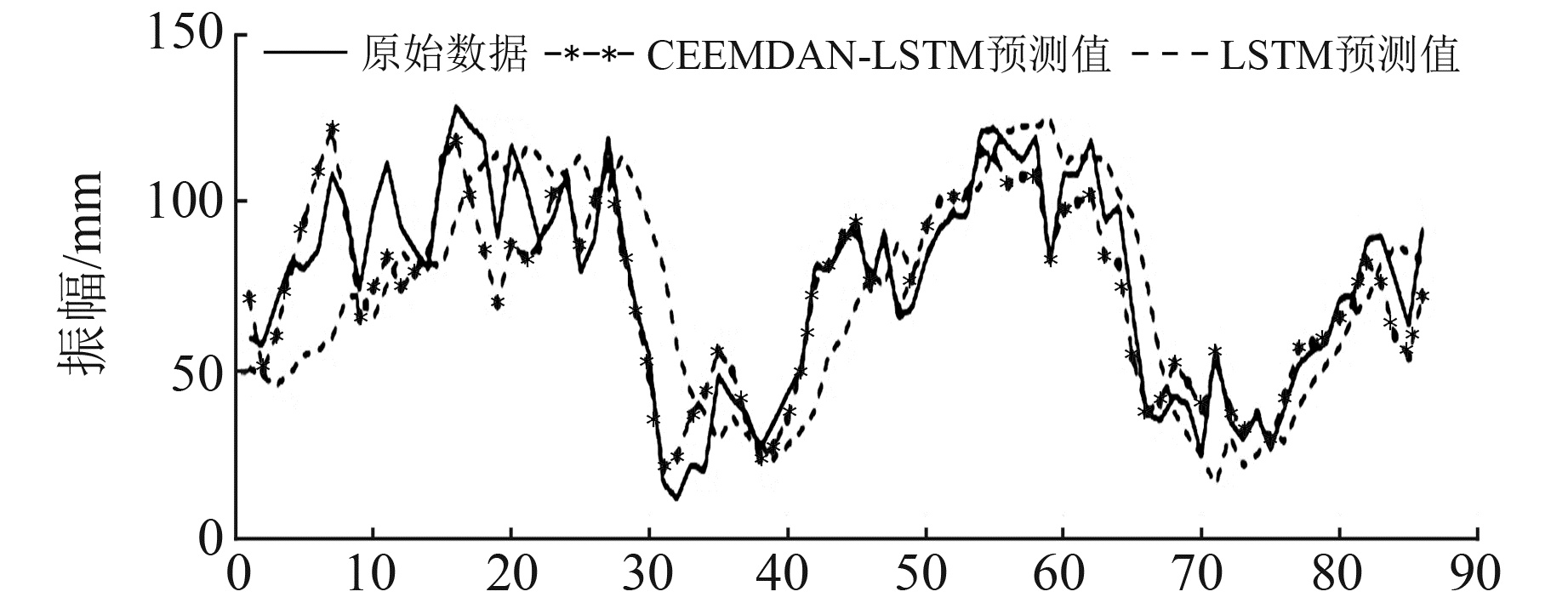
|
图 3 LSTM神经网络预测及CEEMDAN-LSTM组合方法预测结果对比 Fig. 3 Comparison of the prediction results of LSTM neural network prediction and CEEMDAN-LSTM combined model |
除通过图像直观地判断两种方法的预测精度外,本文还采用计算平均绝对误差(MAE)以及均方根误差(RMSE)两项指标进行准确判断,同时引入旧有的研究方法EEMD-BP[10]神经网络组合预测方式进行精度对比,所得结果如表 1(单位mm)所示。可以看出,3种方法均有着不错的精度,均方根误差(RMSE < 22 mm)较低、平均绝对误差(MAE < 17 mm)较小,整体预测效果非常理想。相比之下,CEEEMDAN-LSTM组合方法各项指标明显优于LSTM神经网络和EEMD-BP神经网络组合方法。由此可以得知,使用CEEMDAN-LSTM组合方法对数据进行分解、平稳化和降噪处理,再预测最后重构的方法,其结果优于旧有的EEMD-BP神经网络组合方法以及直接使用LSTM神经网络对原始数据进行预测。
|
|
表 1 LSTM神经网络、EEMD-BP组合方法与CEEMDAN-LSTM神经网络组合方法预测误差比较 Tab. 1 Comparison of prediction errors of LSTM neural network, EEMD-BP combined method and CEEMDAN-LSTM neural network combined method |
本文通过建立CEEMDAN-LSTM组合方法对南海海域1993~2016年间卫星测高海平面异常观测资料进行海平面长期变化趋势预测的研究,与LSTM神经网络预测的方式以及EEMD-BP组合模型进行对比,分析预测模型的精度和适用性。研究结果表明:
1) CEEMDAN分解可以将海平面变化异常序列分解为具有不同周期的变化分量以及趋势项。线性拟合结果显示,1993~2016年南海海平面上升速率达到4.12 mm/a。
2) 通过神经网络对不同的IMF分量建立预测模型,最后将所得结果叠加重构,这种方法所得结果在各个方面都要明显优于直接使用LSTM神经网络进行预测的结果。从不同IMF分量的预测结果来看,当序列逐渐趋于平稳时LSTM神经网络的预测精度有明显提升。
| [1] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995 DOI:10.1098/rspa.1998.0193
(  0) 0) |
| [2] |
蔡念, 黄威威, 谢伟, 等. 基于互补自适应噪声的集合经验模式分解算法[J]. 电子与信息学报, 2015, 37(10): 2 383-2 389 (Cai Nian, Huang Weiwei, Xie Wei, et al. Ensemble Empirical Mode Decomposition Base on Complementary Adaptive Noises[J]. Journal of Electronics and Information Technology, 2015, 37(10): 2 383-2 389)
(  0) 0) |
| [3] |
Wu Z H, Huang N E. Ensemble Empirical Mode Decomposition: A noise-Assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41 DOI:10.1142/S1793536909000047
(  0) 0) |
| [4] |
Yeh J R, Shieh J S, Huang N E. Complementary Ensemble Empirical Mode Decomposition: A Novel Noise Enhanced Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135-156 DOI:10.1142/S1793536910000422
(  0) 0) |
| [5] |
Torres M E, Colominas M A, Schlotthauer G, et al. A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise[C]. 2011 IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP), Prague, Czech Republic, 2011
(  0) 0) |
| [6] |
Hochreiter S, Schmidhuber J. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8): 1 735-1 780 DOI:10.1162/neco.1997.9.8.1735
(  0) 0) |
| [7] |
李文静, 王潇潇. 基于简化型LSTM神经网络的时间序列预测方法[J]. 北京工业大学学报, 2021, 47(5): 480-488 (Li Wenjing, Wang Xiaoxiao. Time Series Prediction Method Based on Simplified LSTM Neural Network[J]. Journal of Beijing University of Technology, 2021, 47(5): 480-488)
(  0) 0) |
| [8] |
潘轶, 岳建平, 宋亚宏, 等. 1993—2015年中国南海海平面变化的初步研究[J]. 地理空间信息, 2017, 15(10): 9-13 (Pan Yi, Yue Jianping, Song Yahong, et al. Initial Research on Sea Level Change in the South China Sea from 1993 to 2015[J]. Geospatial Information, 2017, 15(10): 9-13)
(  0) 0) |
| [9] |
赵健. 中国南海及东海近海测高海平面变化监测与预测[J]. 测绘学报, 2020, 49(5): 670 (Zhao Jian. Sea Level Change Monitoring and Prediction Using Satellite Altimetry in South China Sea and East China Sea Coastal Ocean[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(5): 670)
(  0) 0) |
| [10] |
赵健, 樊彦国, 张音. 基于EEMD-BP组合模型的区域海平面变化多尺度预测[J]. 系统工程理论与实践, 2019, 39(10): 2 713-2 722 (Zhao Jian, Fan Yanguo, Zhang Yin. Multi-Scale Prediction of Regional Sea Level Variations Based on EEMD-BP Combined Model[J]. Systems Engineering-Theory and Practice, 2019, 39(10): 2 713-2 722)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


