2. 沈阳建筑大学交通与测绘工程学院,沈阳市浑南中路25号,110168;
3. 中北大学材料科学与工程学院,太原市学院路3号,030051;
4. 南京农业大学公共管理学院,南京市卫岗1号,210095
从20世纪末开始,GNSS不仅广泛应用于大地测量,而且还广泛应用于大气参数估计[1-3]。当GNSS信号通过大气层时,它会受到电离层和对流层误差的影响。使用两个不同的载波相位和测距码,可以将电离层误差的一阶项从方程中消除[4-5]。然而,电离层误差的二阶项和三阶项误差通常被忽略。随着科学技术的进步和高精度GNSS的应用,如位置或大气参数估计,高阶电离层(HOI)延迟对GNSS的影响已不再可以忽略。GNSS信号因对流层延迟产生的误差只能通过建立相应的模型进行消除。对流层延迟由两部分组成:天顶静力学延迟(zenith hydrostatic delay, ZHD)和天顶湿延迟(zenith wet delay, ZWD)。ZHD通常与大气中气体的浓度有关,而ZWD则与温度、压力和湿度等大气参数有关[2,6]。
对流层延迟和梯度可从GNSS观测中估算,GNSS观测已广泛用于全球和区域层面的大气研究和预测,使用其近实时、实时或后处理解决方案[7-9]。一些学者研究HOI延迟对GNSS定位的影响,Cai等[10]研究HOI对多模GNSS精密单点定位(PPP)的影响,结果表明,HOI延迟可以影响多模GNSS PPP的三维位置解,最大值为6 mm;Zhou等[11]研究HOI延迟对实时动态定位(real time kinematic, RTK)模糊度固定可靠性的影响,结果表明,在电离层活跃期,HOI延迟对双差(double difference, DD)网络解的影响达到7 mm,在GNSS数据处理中可影响模糊度固定成功率达30%,当新卫星出现时,HOI延迟影响更为显著,可改变约0.3%的模糊度修正结果。此外,HOI延迟也会在定位解决方案中引入几mm的误差。
本文通过GAMIT10.71分析澳大利亚地区8个MGEX(multi-GNSS experiment)跟踪站的BDS数据,分别在太阳活动低水平和高水平时期比较HOI延迟对于B2I、B2a和B3I三种频段信号对对流层参数估计的影响。
1 数据与方法 1.1 测站选择考虑到BDS的B2I频段信号主要服务于亚太地区,因此本次实验选择澳大利亚地区的MGEX跟踪站。按照连续性、稳定性、高精度、多种解、平衡性和精度一致性等原则[12],选取8个MGEX跟踪站(ALIC、CEDU、HOB2、KARR、KAT1、MCHL、MOBS、NNOR)。其中,太阳活动低水平时期,通过GAMIT10.71解算MGEX跟踪站BDS数据的日期为2022-08-01~05;太阳活动高水平时期,则为2022-08-25~29。
1.2 算法原理电离层高阶项效应的载波相位和伪距观测方程可表示为:
| $ \left\{\begin{array}{l} {\mathit{\Phi}}_{L i}=\rho^{\prime}+\mathrm{ZTD}-\mathrm{HOI}+c\left(\delta t_{\mathrm{r}}-\delta t^{\mathrm{s}}\right)+ \\ \quad \lambda N_{L i}+\alpha_{\mathrm{r}}-\alpha^{\mathrm{s}}+v_{\Phi_{L i}} \\ \mathrm{PR}_{L i}=\rho^{\prime}+\mathrm{ZTD}+\mathrm{HOI}+ \\ \quad c\left(\delta t_{\mathrm{r}}-\delta t^{\mathrm{s}}\right)+d_{\mathrm{r}}-d^{\mathrm{s}}+v_{\mathrm{PR}_{L i}} \end{array}\right. $ | (1) |
式中,Li(i=1, 2)为信号频率,ρ′为卫星到GNSS接收机之间的几何距离,cδtr和cδts为卫星和接收机的时钟误差,λ为波长,Ni为相位模糊度,αr和dr是接收机硬件误差,αs和ds是卫星硬件误差,vΦLi和vPRLi为相位和伪距残差。
通过使用无电离层组合(ionosphere free, IF)的DD网络解能够消除电离层一阶项延迟,但电离层二阶和三阶项延迟仍然保留。二阶项延迟与电离层折射率上的地磁场有关,而三阶项延迟与射线弯曲误差有关。因此,在高精度GNSS应用中使用地磁场模型是必要的。IGRF(international geomagnetic reference field)模型向用户提供北向、东向和垂直向下方向的地磁场分量。由于信号传播路径上的分量不同,因此在广义坐标系中,IGRF模型数据采用矢量表示。对于每个频率观测值,二阶项(Id,Li(2))可表示为:
| $ I_{d, L i}^{(2)}=\frac{e A}{f_{L i}^3 2 \pi m_{\mathrm{e}}}\|\boldsymbol{B}\||\cos \theta| \mathrm{TEC} $ | (2) |
三阶项(Id,Li(3))可以表示为:
| $ I_{d, L i}^{(3)}=\frac{3 A^2}{8 f_{L i}^4} \eta N_{e, \max } \text { TEC } $ | (3) |
式中,A=80.6 m3/s2,e=1.602 18×10-19为库仑电子,me=9.109 39×10-31 kg为电子质量,||B||为地磁感应矢量B的大小,η为函数因子(常取近似值0.66),Ne, max为电子峰值密度,信号传播路径中的TEC可表示为:
| $ \begin{gathered} \mathrm{TEC}=\frac{f_{L 1}^2 f_{L 2}^2}{40.3\left(f_{L 1}^2-f_{L 2}^2\right)} \cdot \\ \left(\mathrm{PR}_{L 1}-\mathrm{PR}_{L 2}-c\left(\mathrm{DCB}_{\mathrm{r}}+\mathrm{DCB}_{\mathrm{s}}\right)+\varepsilon_{L 1 L 2}\right) \end{gathered} $ | (4) |
式中,fLi(i=1, 2)是GNSS信号频率,DCBr和DCBs分别是接收机和卫星的差分码偏差(即两个频率间的硬件延迟),c为真空中的光速,εL1L2为所有未建模的残差效应。
通过GAMIT10.71软件分别处理HOI校正前后的BDS数据,使用相同的处理策略,即IF的线性组合(linear combination, LC)、Saastamoinen模型和全球映射函数(global mapping function,GMF)模型。此外,GAMIT10.71软件的DD网络解方案中使用了FES2004全球海潮模型、ITRF2014固体潮模型、USNO Bulletin-b地球定向参数模型、13参数ECOMC光压模型以及CODE(Center for Orbit Determination in Europe)时钟和轨道参数的最终产品。最终,GAMIT10.71的对流层延迟和梯度输出的时间分辨率设置为1 h。对流层延迟可表示为:
| $ \begin{gathered} T_d=T_{\mathrm{W} d}+T_{\mathrm{D} d}=T_{\mathrm{ZW} d} \mathrm{MF}_{\mathrm{wet}(\varepsilon)}+ \\ T_{\mathrm{ZD} d} \mathrm{MF}_{\mathrm{dry}(\varepsilon)}+A_{d(\varepsilon, \alpha)} \end{gathered} $ | (5) |
式中,Td为对流层延迟,TWd和TDd为对流层干、湿延迟,TZDd和TZWd为天顶干、湿延迟,MFdry和MFwet分别为干、湿映射函数,ε为卫星高度角。大气延迟中Ad(ε,α)的方位不对称效应包含在模型中,可表示为:
| $ \begin{gathered} A_{d(\varepsilon, a)}=\mathrm{NS}_{\mathrm{grad}} \cos \alpha \mathrm{MF}(\varepsilon)+\mathrm{EW}_{\mathrm{grad}} \sin \alpha \mathrm{MF}(\varepsilon), \\ \mathrm{MF}_{\varepsilon}=\frac{1}{\sin \varepsilon \tan \varepsilon+0.0032} \end{gathered} $ | (6) |
式中,α为方位角,NSgrad和EWgrad分别是南北梯度和东西梯度,MF(ε)是梯度的映射函数。
综上所述,MGEX跟踪站BDS数据处理策略之间的唯一区别在于是否应用HOI的电离层模型文件IONEX。通过式(1)中表示的数学模型,估算选定MGEX跟踪站的对流层ZTD和梯度。在载波相位模糊、站坐标固定、使用卫星轨道和时钟相同的情况下,作为未知数进入方程的唯一参数是ZTD、梯度分量NSgrad和EWgrad。因此,DD网络解的估计参数向量可表示为:
| $ \boldsymbol{X}=\left(\overline{\mathrm{ZTD}}, \mathrm{NS}_{\mathrm{grad}}, \mathrm{EW}_{\mathrm{grad}}\right), \overline{\mathrm{ZTD}}=T_{\mathrm{ZW} d}+T_{\mathrm{ZD} d} $ | (7) |
中国空间环境预报中心发布太阳活动状况如表 1所示,2022-08-01~05太阳活动整体处于极低水平状态,其中08-05射电流量和太阳黑子数较高,但仍处于太阳活动低水平状态。
|
|
表 1 太阳活动低水平时期状况 Tab. 1 Status of low solar activity |
统计BDS的ZTD在HOI延迟改正前后差值(difference, Diff)的均值(mean)和均方根值(RMS),如表 2(单位mm)所示。综合比较HOI延迟改正前后MGEX跟踪站BDS的ZTD差值mean和RMS,并绘制出mean和RMS综合数值较大的MGEX跟踪站BDS的ZTD和ZTD差值的时间序列图(图 1)。
|
|
表 2 ZTD差值mean和RMS Tab. 2 Mean and RMS values of the ZTD |

|
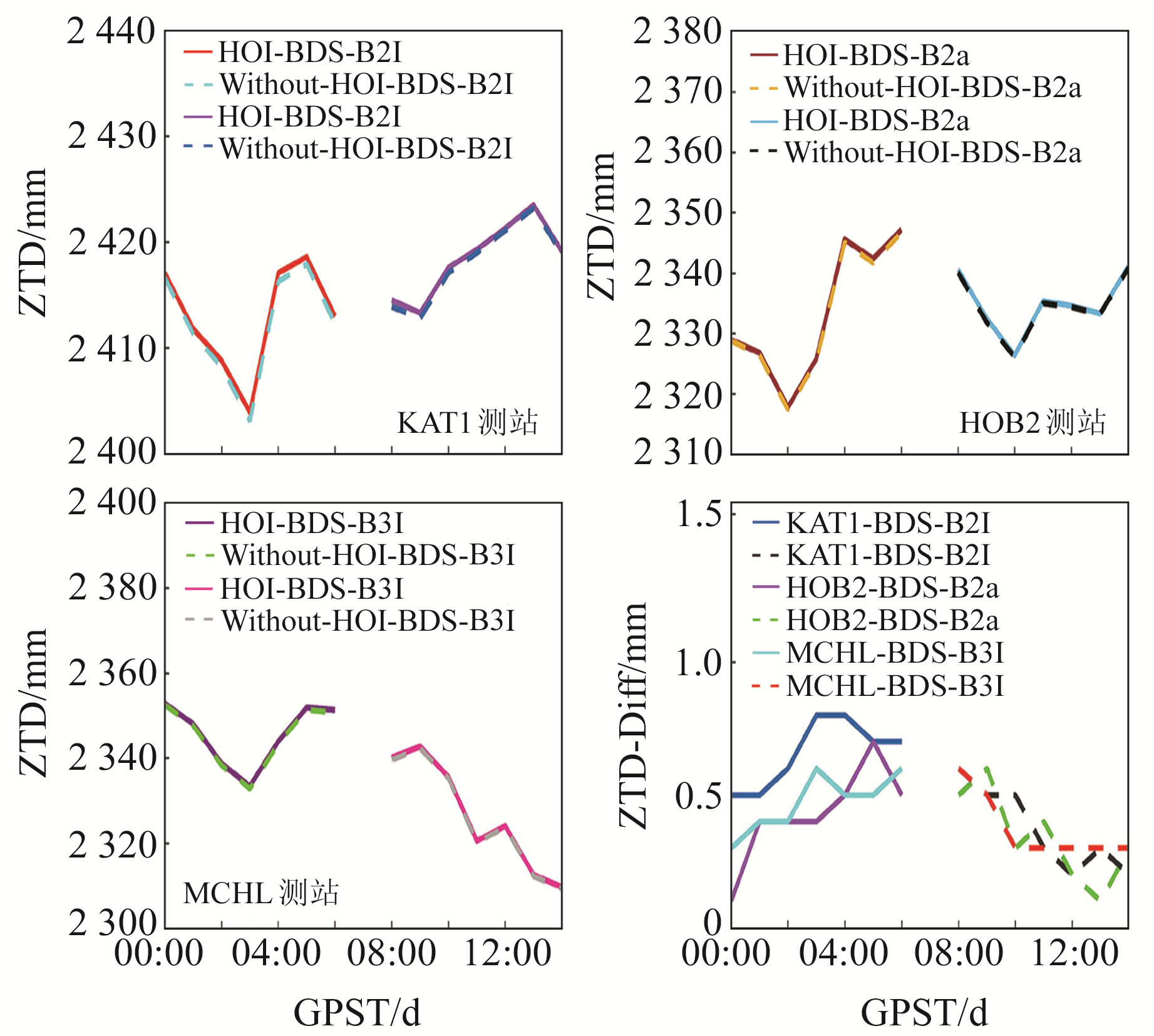
图 1 ZTD和ZTD差值时间序列 Fig. 1 Time series of the ZTD and ZTD differences |
由图 1可知,KAT1测站B2I的ZTD时间序列图整体重合较好,没有明显差异,ZTD差值峰值出现在GPS时(GPST)08-01 3:00,达到0.80 mm;HOB2测站B2a的ZTD时间序列图出现几处明显偏差,ZTD差值峰值出现在GPST 08-05 20:00,达到3.60 mm;MCHL测站B3I的ZTD时间序列图整体一致性较好,ZTD差值峰值出现在GPST 08-03 14:00,达到1.60 mm。
统计BDS的梯度在HOI延迟改正前后的差值mean和RMS值,如表 3(单位mm)所示。综合比较HOI延迟改正前后MGEX跟踪站BDS的梯度差值mean和RMS值,并绘制mean和RMS综合数值较大的MGEX跟踪站BDS的梯度和梯度差值的时间序列图(图 2,图 3)。
|
|
表 3 南北和东西梯度差值mean和RMS Tab. 3 Mean and RMS values of the NS and EW gradients differences |
|
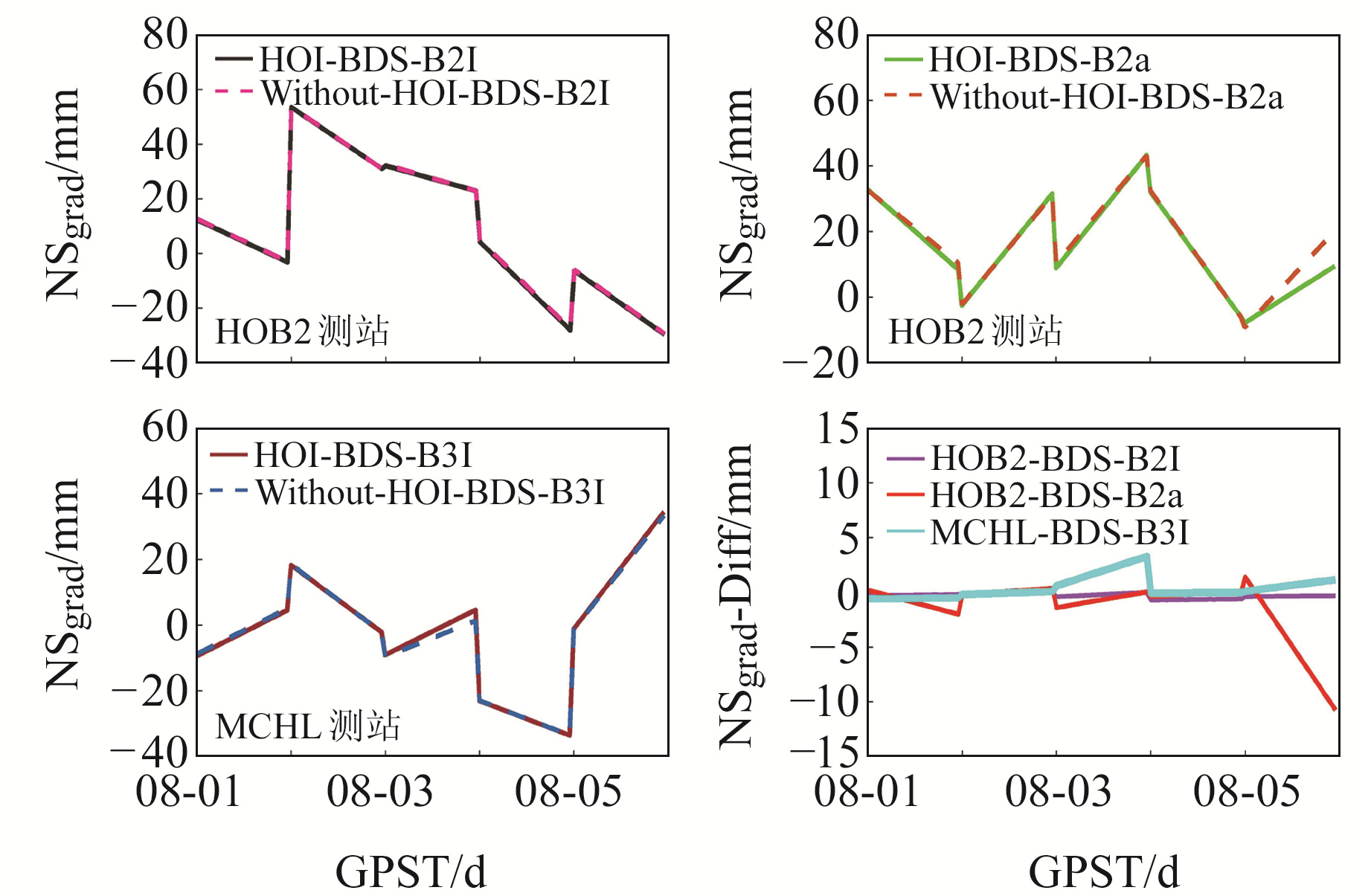
图 2 NSgrad和NSgrad差值时间序列 Fig. 2 Time series of the NS gradients and NS gradients differences |

|
图 3 EWgrad和EWgrad差值时间序列 Fig. 3 Time series of the EW gradients and EW gradients differences |
通过图 2和图 3可知,HOB2和KAT1测站B2I的NSgrad和EWgrad时间序列图整体一致性较好,没有出现明显偏差。NSgrad和EWgrad差值峰值出现在GPST 08-03 00:00和23:00,分别达到0.60 mm和0.99 mm。HOB2和ALIC测站B2a的NSgrad和EWgrad时间序列出现几处明显的不重合。NSgrad和EWgrad差值峰值均出现在GPST 08-06 23:00,分别达到10.77 mm和10.74 mm。MCHL测站B3I的NSgrad和EWgrad时间序列图整体一致性较好,但在08-03出现明显偏差。NSgrad和EWgrad差值峰值出现在GPST 08-03 23:00和00:00,分别达到3.28 mm和5.90 mm。
2.1.2 HOI在昼夜对流层ZTD估计中的影响进一步研究HOI延迟对于白天(day time)和夜晚(night time)ZTD估计的影响。为便于研究,本次实验仅绘制部分白天(GPST 00:00~06:00)和夜晚(GPST 08:00~14:00)的ZTD和ZTD差值时间序列,图 4展示08-01白天和夜晚时间序列,图 5统计了8个MGEX跟踪站白天和夜晚的ZTD差值均值。
|
图 4 2022-08-01 ZTD差值时间序列 Fig. 4 Time series of the ZTD differences on August 1 |

|
图 5 MGEX跟踪站昼夜ZTD差值均值 Fig. 5 Daytime and nighttime ZTD differences mean of MEGX tracking stations |
由图 4可见,2022-08-01 KAT1测站的B2I、HOB2测站的B2a和MCHL测站的B3I在白天对应的GPST 00:00-06:00时段内,ZTD差值时间序列曲线整体呈现上升的趋势,在夜晚对应的GPST 8:00-14:00时段内,ZTD差值时间序列曲线整体呈现下降的趋势。
由图 5可见,2022-08-01~05 B2I和B3I的8个MGEX跟踪站HOI延迟对于ZTD的影响均表现为白天远高于夜晚,而B2a的ALIC、HOB2和MCHL测站出现异常,这可能与这3个测站追踪的IGSO卫星的B2a频段信号丢失有关。进一步观察可以发现,HOI延迟对于昼夜的B2a影响较小,B2I则较大。
2.2 太阳活动高水平时期中国空间环境预报中心发布的太阳活动状况如表 4所示,2022-08-25~ 08-29太阳活动整体处于高水平状态,其中08-28射电流量达到峰值,黑子相对数较高,太阳活动处于极高水平状态。
|
|
表 4 太阳活动高水平时期状况 Tab. 4 Status of high solar activity |
使用§2.1相同的研究方法,绘制出mean和RMS综合数值较大的MGEX跟踪站BDS的ZTD和ZTD差值以及梯度和梯度差值的时间序列图(图 6~8)。

|
图 6 ZTD和ZTD差值时间序列 Fig. 6 Time series of the ZTD and ZTD differences |
|
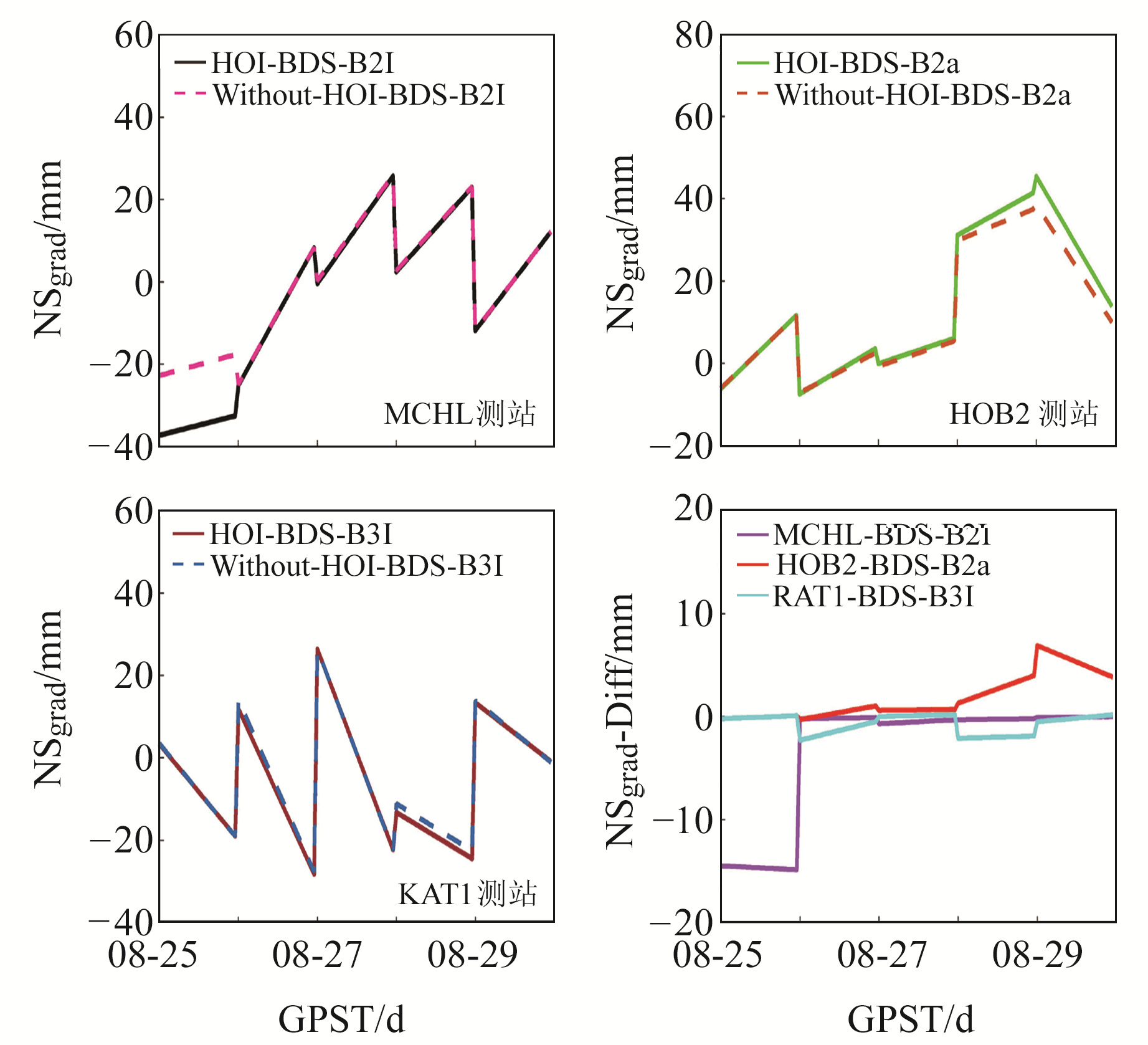
图 7 NSgrad和NSgrad差值时间序列 Fig. 7 Time series of the NS gradients and NS gradients differences |
|
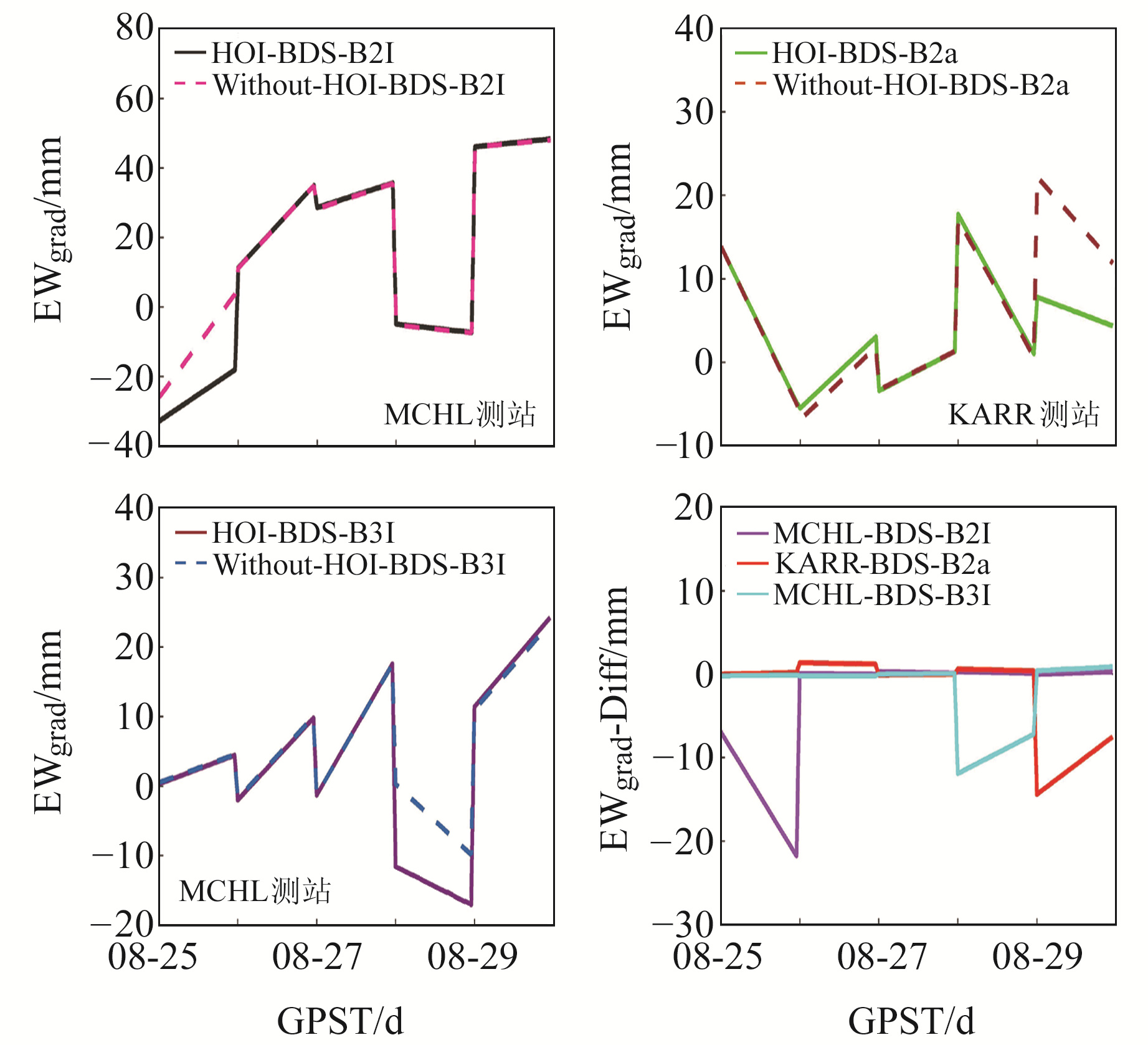
图 8 EWgrad和EWgrad差值时间序列 Fig. 8 Time series of the EW gradients and EW gradients differences |
由图 6可见,KARR测站B2I的ZTD时间序列在GPST 08-25出现明显偏差,ZTD差值峰值出现在GPST 08-25 00:00零时,达到6.20 mm;CEDU测站B2a的ZTD时间序列出现多处明显偏差,ZTD差值峰值出现在GPST 08-28 13:00,达到9.00 mm;MCHL测站B3I的ZTD时间序列整体一致性较好,ZTD差值峰值出现在GPST 08-27 08:00,达到3.30 mm。
通过图 7和图 8可知,MCHL测站B2I的NSgrad和EWgrad时间序列在GPST 08-25出现明显偏差,NSgrad和EWgrad差值峰值均出现在GPST 08-25 00:00,分别达到14.88 mm和21.75 mm。HOB2和KARR测站的B2a的NSgrad和EWgrad时间序列出现多处明显的不重合,NSgrad和EWgrad差值峰值均出现在GPST 08-29 00:00,分别达到6.90 mm和14.40 mm。KAT1和MCHL测站的B3I的NSgrad和EWgrad时间序列整体一致性较好,但在GPST 08-26和08-28出现明显偏差,NSgrad和EWgrad差值峰值出现在GPST 08-26 00:00和08-28 00:00,分别达到2.30 mm和11.90 mm。
3 结语本文通过GAMIT10.71分别处理太阳活动低水平和高水平时期的MGEX跟踪站BDS数据,计算对流层ZTD和梯度差值mean和RMS,比较BDS的B2I、B2a和B3I三种频段信号的ZTD和梯度以及差值时间序列,分析HOI延迟对于BDS的B2I、B2a和B3I三种频段信号对对流层参数估计的影响。
实验结果表明,太阳活动低水平时期,HOI延迟对B2I影响最小,对B2a影响最大。太阳活动高水平时期,HOI延迟对B2I、B2a和B3I三种频段信号产生了更大的影响,其中,B2I、B2a和B3I三种频段信号的EWgrad影响最大分别达到21.75 mm、14.40 mm和11.90 mm。实验结果进一步表明,B3I受太阳活动影响整体较小,更适合应用在高精度GNSS服务中;HOI延迟对于BDS对流层参数估计的影响白天高于夜晚、低纬度地区高于高纬度地区。
| [1] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research, 1992, 97(D14)
(  0) 0) |
| [2] |
Bevis M, Businger S, Chiswell S, et al. GPS Meteorology: Mapping Zenith Wet Delays Onto Precipitable Water[J]. Journal of Applied Meteorology, 1994, 33(3): 379-386 DOI:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2
(  0) 0) |
| [3] |
Businger S, Chiswell S R, Bevis M, et al. The Promise of GPS in Atmospheric Monitoring[J]. Bulletin of the American Meteorological Society, 1996, 77(1): 5-18 DOI:10.1175/1520-0477(1996)077<0005:TPOGIA>2.0.CO;2
(  0) 0) |
| [4] |
Yuan Y B, Zhang K F, Rohm W, et al. Real-Time Retrieval of Precipitable Water Vapor from GPS Precise Point Positioning[J]. Journal of Geophysical Research: Atmospheres, 2014, 119(16): 10 044-10 057 DOI:10.1002/2014JD021486
(  0) 0) |
| [5] |
Gurbuz G, Jin S G. Long-Time Variations of Precipitable Water Vapour Estimated from GPS, MODIS and Radiosonde Observations in Turkey[J]. International Journal of Climatology, 2017, 37(15): 5 170-5 180 DOI:10.1002/joc.5153
(  0) 0) |
| [6] |
Rocken C, Van Hove T, Johnson J, et al. GPS/STORM-GPS Sensing of Atmospheric Water Vapor for Meteorology[J]. Journal of Atmospheric and Oceanic Technology, 1995, 12(3): 468-478 DOI:10.1175/1520-0426(1995)012<0468:GSOAWV>2.0.CO;2
(  0) 0) |
| [7] |
Jin S, Park J U, Cho J H, et al. Seasonal Variability of GPS-Derived Zenith Tropospheric Delay(1994-2006) and Climate Implications[J]. Journal of Geophysical Research: Atmospheres, 2007, 112(D9)
(  0) 0) |
| [8] |
Jin S G, Li Z, Cho J. Integrated Water Vapor Field and Multiscale Variations over China from GPS Measurements[J]. Journal of Applied Meteorology and Climatology, 2008, 47(11): 3 008-3 015 DOI:10.1175/2008JAMC1920.1
(  0) 0) |
| [9] |
Jin S G, Luo O F. Variability and Climatology of PWV from Global 13-Year GPS Observations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(7): 1 918-1 924 DOI:10.1109/TGRS.2008.2010401
(  0) 0) |
| [10] |
Cai C S, Liu G, Yi Z H, et al. Effect Analysis of Higher-Order Ionospheric Corrections on Quad-Constellation GNSS PPP[J]. Measurement Science and Technology, 2019, 30(2)
(  0) 0) |
| [11] |
Zhou H T, Wang L, Fu W, et al. Impact of Higher-Order Ionospheric Delay on the Reliability of RTK Ambiguity Estimation[J]. Advances in Space Research, 2022, 69(1): 727-736 DOI:10.1016/j.asr.2021.09.031
(  0) 0) |
| [12] |
曹炳强, 成英燕, 许长辉, 等. 间距分区法在解算卫星连续运行站数据中的应用[J]. 测绘通报, 2016(11): 15-17 (Cao Bingqiang, Cheng Yingyan, Xu Changhui, et al. Application of Space Partition Method in the CORS Data Processing[J]. Bulletin of Surveying and Mapping, 2016(11): 15-17)
(  0) 0) |
2. School of Transportation and Geomatics Engineering, Shenyang Jianzhu University, 25 Mid-Hunnan Road, Shenyang 110168, China;
3. School of Materials Science and Engineering, North University of China, 3 Xueyuan Road, Taiyuan 030051, China;
4. College of Public Administration, Nanjing Agricultural University, 1 Weigang, Nanjing 210095, China
 2023, Vol. 43
2023, Vol. 43


