目前,中国北斗卫星导航系统BDS在轨提供服务的卫星达到45颗,包括15颗北斗二号卫星和30颗北斗三号卫星[1]。北斗二号卫星由中国空间技术研究院(CAST)制造,北斗三号卫星由CAST和中国科学院上海微小卫星工程中心(SECM)制造。混合星座结构、更大的全球跟踪网络观测数据、全球内更多更均匀分布监测站、多样化天线等新特点推动了天线相位中心改正PCC模型的不断更新和改进,PCC模型由天线相位中心偏差PCO和天线相位中心变化(phase center variation, PCV)组成。
国际GNSS服务(international GNSS service, IGS)组织于1996年开始对接收机相位中心进行观测值改正,改正模型经历了由最初的相对模型到目前采用的改正精度较高的绝对模型[2]。目前,IGS发布的最新igs14.atx文件中给出了大部分大地测量型接收机天线的GPS/GLONASS系统PCC模型,但仅有极少部分天线提供北斗系统的PCC模型[3]。考虑到缺乏接收机端BDS B1I和B3I频点的PCC模型,因此一般采用接收机GPS L1/L2频点的PCC模型分别代替或者忽略[4]。IGS在第3次重处理(IGS repro 3, IGS R3)中公布的igsR3_2077.atx中包含部分接收机在IGb R3框架下的北斗PCC模型,涵盖大多数北斗卫星精密定轨使用的测站,为北斗系统精密数据处理中接收机天线的PCC模型提供了新选择。PCC模型对卫星精密定轨中保持参考框架的一致性和多系统解的一致性至关重要,对于高精度的定位和测量,天线相位中心改正必须全面考虑,其对于站点坐标,特别是高程方向不容忽视[5]。对此,国内外学者已作过大量研究。Dilssner等[6]对北斗IGSO和MEO上L波段发射天线阵列进行早期相位中心修正;Dach等[7]研究认为,采用更新后的GLONASS天线相位中心模型有助于提高轨道质量;Qu等[8]对IGb 14和IGS R3框架下的北斗IGSO和MEO卫星相位中心校正进行研究,结果表明,轨道一致性受益于在轨标定的PCO/PCV模型;Yan等[9]利用GNSS地面跟踪数据在轨估计北斗三号MEO卫星的高精度PCO和PCV;Araszkiewicz等[10]研究天线相位中心模型对测站坐标的影响;Xia等[11]比较不同SRP模型在北斗PCO估计中的性能;王嘉琛等[3]采用历元间差分方法对接收机天线多个频点的PCO和PCV分别进行标定和拟合;胡新乔等[12]从定位角度验证利用GPS代替BDS天线相位中心改正参数策略的有效性;Huang等[13]利用PCO参数模型估计北斗二号IGSO和MEO卫星的相位中心偏移。尽管国内外已有大量PCO和PCV模型相关研究,但大多数针对GPS系统以及卫星端,较少涉及BDS接收机端天线相位中心模型的性能分析。通常,接收机主要采用室外标定和德国汉诺威大学及Geo++公司提出的绝对天线相位中心标定方法——机器人标定法,后续研究则主要集中在接收机天线相位中心误差处理方面[14]。
本文首先明确接收机天线相位中心模型及其特性,通过将GPS系统IGb R3与IGb 14标定值进行比较,验证在未提供北斗接收机天线IGb 14标定值的情况下采用IGb R3标定值代替的可行性;然后对北斗卫星精密定轨中接收机PCC模型分别采用IGb R3标定值代替、GPS L1/L2频点值代替以及PCC赋0三组模型进行对比,分析3种模型在精密定轨中的性能差异,建立当前北斗精密定轨接收机PCC模型最优化策略;再采用PCC赋0模型进行单北斗系统定轨,分析接收机PCC误差对卫星定轨性能的影响;最后针对BDS接收机天线相位中心改正模型的应用提出建议和展望。
1 接收机天线相位中心及改正模型接收机天线相位中心与天线参考点(antenna reference point, ARP)不一致会导致天线相位中心改正(PCC)误差[15]。其中,PCO是指天线平均相位中心(mean phase center, MPC)和ARP之间的改正;GNSS信号实际测量的天线瞬时相位中心与平均相位中心MPC的差值称为PCV[16]。
由于IGS天线文件中给出的PCO值是在测站地平坐标系下的3个分量(N、E、U),因此首先将其转换到地心地固系,再对测站坐标进行偏差改正;PCV改正首先根据信号入射高度角和方位角进行内插,然后再将其改正到几何距离观测值中[17]。具体过程如下:
1) 利用旋转矩阵将局部坐标系中的偏心矢量转换至地固坐标系:
| $ \Delta \boldsymbol{r}_k=\boldsymbol{r}_k-\boldsymbol{r}_E $ | (1) |
| $ \begin{gathered} \Delta \boldsymbol{r}_{\mathrm{ek}}=\boldsymbol{R}_H\left(270^{\circ}-\lambda\right) \boldsymbol{R}_E\left(\varphi-90^{\circ}\right) \Delta \boldsymbol{r}_k= \\ {\left[\begin{array}{ccc} -\sin \lambda & -\cos \lambda \sin \varphi & \cos \lambda \sin \varphi \\ \cos \lambda & -\sin \lambda \sin \varphi & \sin \lambda \cos \varphi \\ 0 & \cos \varphi & \sin \varphi \end{array}\right]} \end{gathered} $ | (2) |
式中,Δrk为PCO值,接收机PCO一般使用局部坐标表示,由天线相位中心相对于基点的垂直方向偏差ΔU、北方向偏差ΔN和东方向偏差ΔE表示;rk、rE为地固坐标系中接收机相位中心和ARP的位置矢量;λ、φ分别为测站地心经度、纬度;RH、RE为旋转矩阵;Δrek为地心地固系下的PCO值。
2) 接收机相位中心偏差对观测距离的影响Δρk可表示为:
| $ \Delta \boldsymbol{\rho}_k=\Delta \boldsymbol{r}_{\mathrm{ek}} \cdot \hat{\boldsymbol{\rho}} $ | (3) |
式中,
3) 接收机天线改正项可表示为:
| $ \Delta \boldsymbol{r}(a, e)=\Delta \boldsymbol{r}_{\mathrm{PCV}}(a, e)+\Delta \boldsymbol{\rho}_k $ | (4) |
式中,Δr (a,e)、ΔrPCV(a,e)分别为与方位角a和高度角e相关的接收机PCC、PCV改正值。
2 接收机天线PCC差异及特性在IGb 14框架下北斗B1I/B3I频点精密数据处理中接收机PCC模型采用GPS L1/L2值替代或IGb R3值替代均与理论值存在一定差异,其中理论值与GPS L1/L2值之间的差异可抽象为同一框架间不同系统PCO值的差异(以下简称系统间);理论值与IGb R3值之间的差异可抽象为同一系统间不同框架PCO值的差异(以下简称框架间),与理论值差异越小则越可能获得更优的定轨效果。利用igs14_wwww.atx、igsR3_2077.atx分别统计不同接收机天线不同系统PCO各分量的标定值和差异,对接收机天线PCC进行定量分析。其中,igs14_wwww.atx为IGS提供的基于IGb 14地球参考框架的包含卫星和接收机天线相位校正值的文件;igsR3_2077.atx为基于IGb R3地球参考框架的包含卫星和接收机天线相位校正值的文件。
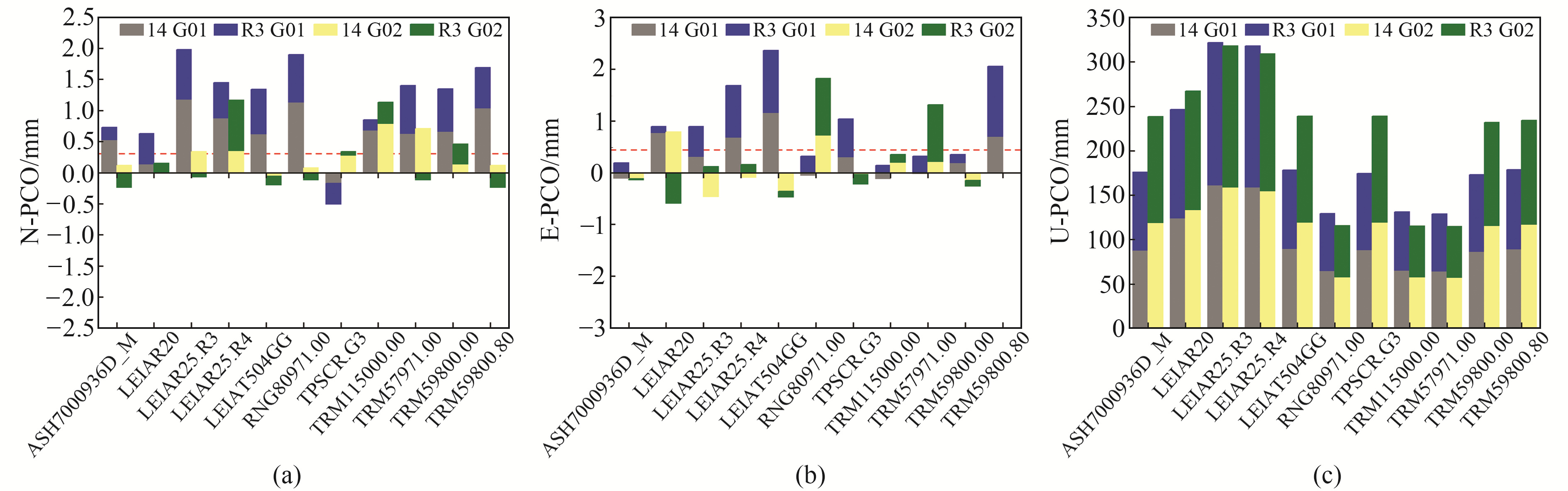
2.1 同一系统不同框架间PCO差异比较igs14_wwww.atx以及igsR3_2077.atx中各接收机天线均提供GPS系统的PCO改正值,统计11种接收机天线分别在IGb 14框架与IGb R3框架下的PCO值及其差异。图 1为GPS接收机IGb14框架PCO与IGb R3框架下N、E、U三个方向的PCO值,红色虚线表示2组框架下PCO差异值的算术平均值。需要说明的是,U方向(图 1(c))相较于刻度变化量不明显,其算术平均值约为0.4 mm。由图可知,对于同一GPS系统IGb R3和IGb 14框架下接收机各个方向PCO模型值之差一般小于0.5 mm,差异较小。
|
图 1 IGb 14框架与IGb R3框架下接收机GPS系统PCO值及差异 Fig. 1 PCO value and difference of receiver in the GPS system under IGb 14 frame and IGb3 frame |
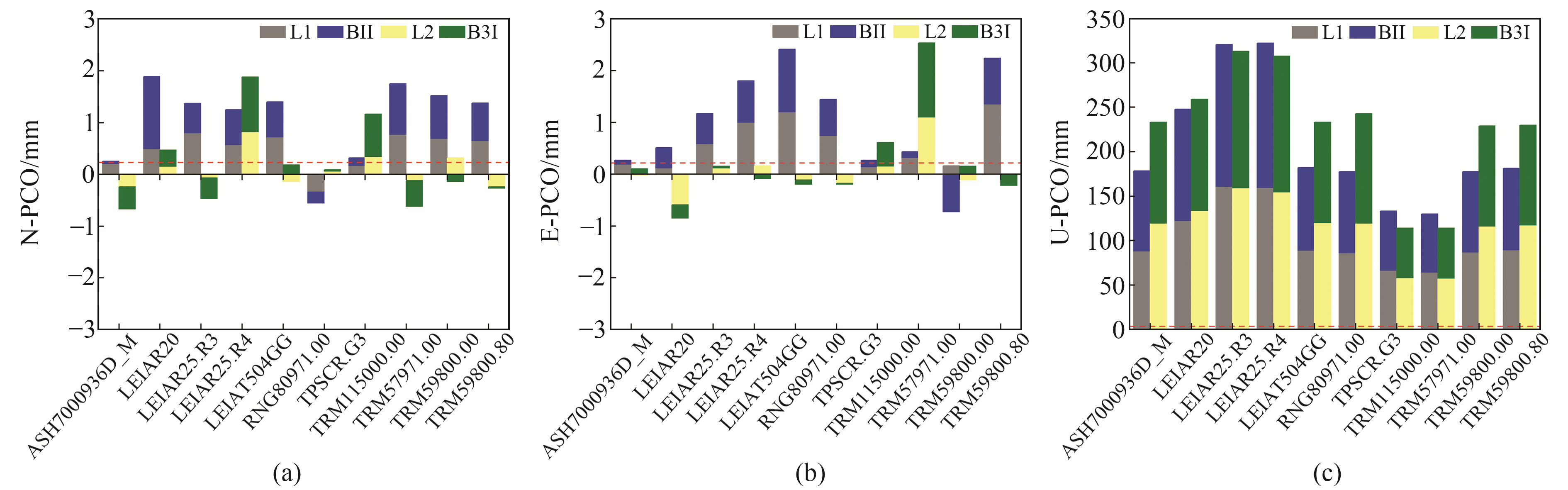
igsR3_2077.atx中部分接收机天线同时提供GPS L1/L2与BDS B1I/B3I频点的PCO改正值。选取10种接收机天线,图 2为接收机端天线在GPS L1/L2以及BDS B1I/B3I频点上PCO的标定值及L1/B1I、L2/B3I频点之间的差异。结果表明,不同天线在同一频点的相位中心校正值在平面方向的差异通常在mm级,而在高程方向差异达cm级;同一天线不同频点的相位中心校正值在高程方向差异较大[18]。以天线LEIAT504GG/NONE为例,其在高程方向上L1和B1I频点相位中心改正值差异达4.3 mm,L2和B3I频点差异达6.1 mm。
|
图 2 接收机端天线GPS及BDS频点相位中心改正比较 Fig. 2 Comparison of receiver antenna frequencies phase center correction between GPS and BDS |
表 1(单位mm)为上述2种方案在N、E、U方向上相位中心改正差异绝对值的平均值统计结果。可以看出,对于接收机天线,在水平方向系统间差异与框架间差异较小,均未超过0.5 mm,在高程方向系统间差异则远大于框架间差异,U方向框架间平均差异为0.4 mm,而系统间平均差异则达到3.38 mm。因此,可以认为IGb 14框架下北斗B1I/B3I PCO理论值与北斗B1I/B3I IGb R3值之间的差异小于IGb 14框架下GPS L1/L2值,初步证明在IGb 14框架下北斗B1I/B3I频点精密数据处理中,未提供北斗接收机天线IGb 14标定值情况下采用IGb R3标定值代替优于采用IGb 14框架下GPS L1/L2值代替。IGb 14框架下接收机北斗系统PCC模型仍需标定,特别是在高程方向。
|
|
表 1 N、E、U方向相位中心改正差异的绝对值均值 Tab. 1 Average absolute value of phase center correction difference inN,E andU directions |
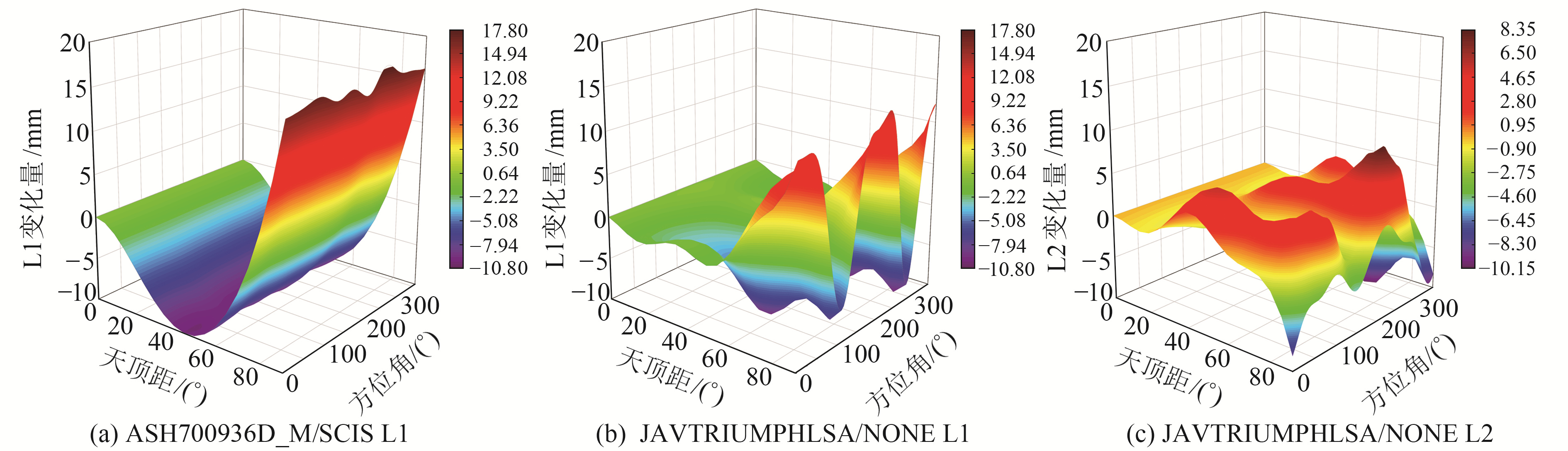
图 3为不同接收机天线不同频点的PCV标定值。以图 3(a)天线为例可知,ASH700936D_M/SCIS天线L1频点的相位中心变化受天顶距变化影响较大,方位角变化次之。在天顶距为45°时,PCV达到负向最大值,在天顶距接近90°时达到正向最大值,在天顶距接近0°,即卫星高度角90°时相位中心变化最小。对比图 3(a)和3(b)可知,不同天线同一频点的PCV有所不同且变化趋势存在差异;对比图 3(b)和3(c)可知,同一天线不同频点的PCV也存在一定差异,天线PCV与高度角和方位角相关,一般高度角对其影响较大,方位角对其影响较小[19]。
|
图 3 接收机天线PCV Fig. 3 PCV ofreceiver antenna |
综上所述,对于接收机天线,同系统不同框架间的PCO差异不大,均未超过0.5 mm。而同一框架不同系统和频点间的PCO在U方向差异最大为3.38 mm。因此,在进行卫星精密定轨时,顾及同一框架不同系统和频点间差异,为提高定轨精度,须进行接收机天线相位中心改正。
3 精密定轨算例分析本文利用2021年年积日(day of year, doy) 180~195约120个全球均匀分布的MGEX(the multi-GNSS experiment)跟踪站数据进行精密定轨,为保证框架与IGb 14对齐,采用北斗B1I/B3I频点数据和GPS L1/L2数据联合定轨,将测站坐标紧约束至IGS公布的SNX文件中提供的精确坐标,北斗和GPS卫星端PCC均固定至igs14_wwww.atx。主要处理策略及模型见表 2。
|
|
表 2 数据处理策略 Tab. 2 The data processing strategies |
为分析不同接收机天线北斗系统PCC模型性能,设计3种方案进行精密定轨:方案1,接收机天线北斗PCC采用IGb R3标定值,简称为GC_R3;方案2,接收机天线北斗PCC采用IGb 14框架的GPS L1/L2改正代替,简称为GC_G;方案3,接收机天线北斗PCC赋值为0,简称为GC_0。
将相邻2 d精密轨道进行拟合,计算2 d弧段拟合残差的1D RMS值作为精密轨道精度的评价标准,该方法可以评价精密轨道的内符合精度。图 4为3种方案各卫星的拟合精度平均值,表 3(单位mm)为根据卫星类型总结各方案轨道拟合1D RMS精度。

|
图 4 3种方案下不同北斗卫星轨道2D拟合精度 Fig. 4 2D fitting accuracy of different Beidou satellite orbits under three schemes |
|
|
表 3 各方案轨道拟合精度1D RMS Tab. 3 1D RMS of orbit fitting accuracy of each scheme |
由表可见,对于北斗二号IGSO、MEO,方案2的平均轨道拟合精度优于方案1。对于北斗三号CAST-MEO、SECM-MEO和IGSO,与方案2相比,方案1北斗三号CAST MEO、SECM MEO和IGSO的平均轨道拟合1D RMS分别减少约0.51 mm(2.4%)、2.32 mm(9.75%)和0.97 mm(1.57%),方案1结果优于方案2。北斗二号各方案的定轨精度呈现出与北斗三号不同的特性,对于IGSO卫星,方案3结果最优;对于MEO卫星,方案2结果最优。但由于IGSO卫星的区域分布特性和较高的轨道高度会造成较小的天底角范围,其对PCC垂直方向的改正并不敏感。北斗二号MEO卫星由于数量较少,其定轨精度也较北斗三号MEO卫星差,其定轨结果可能具有一定偶然性,或受到其他误差改正项影响。北斗三号MEO卫星的结果更具参考性,因此在未提供IGb 14框架下接收机天线北斗标定值情况下,北斗精密数据处理推荐采用IGb R3框架下的北斗标定值。
值得注意的是,GC_0即接收机天线北斗PCC赋0方案中,北斗二号及北斗三号MEO卫星的定轨精度显著降低,IGSO卫星本身定轨精度较低且对PCC垂直方向的改正并不敏感,其影响则较小,北斗二号IGSO卫星结果略优于GC_R3、GC_G方案,北斗三号IGSO卫星结果略差于GC_R3、GC_G方案。
为进一步研究接收机PCC对定轨精度的影响,并分析GC_0方案MEO卫星定轨精度显著降低的原因,设计方案4作为对比,排除GPS系统对框架和公共参数的贡献,进行单北斗系统精密定轨,接收机天线北斗PCC赋值为0,其余策略与表 2相同,该方案简称为C_0。
图 5为C_0与GC_0方案的轨道拟合1D RMS精度,并选取GC_R3轨道拟合1D RMS精度为基准作为对比。表 4(单位mm)为根据不同方案总结北斗二号、北斗三号MEO卫星的平均轨道拟合1D RMS精度。由表可见,相比于GC_0方案,C_0方案MEO卫星定轨精度显著提升,但整体上仍然比GC_R3方案差。由此可知,在北斗和GPS双系统定轨时,由于GPS系统具有更多的观测值和更高的定轨精度,GPS和北斗系统轨道的参考框架以及接收机钟差等公共参数紧约束至GPS解,由于测站坐标进行紧约束,接收机天线北斗PCC的误差则被更多地传递到北斗轨道中。在单北斗系统定轨时,由于没有GPS框架等限制,接收机天线北斗PCC的误差则更容易被接收机钟差等参数吸收,因此,C_0方案的定轨精度显著优于GC_0方案,但由于其仍存在更多模型误差,北斗三号MEO卫星的定轨精度仍明显差于GC_R3方案。

|
图 5 3种方案下不同北斗卫星轨道2D拟合精度 Fig. 5 2D fitting accuracy of different Beidou satellite orbits under three schemes |
|
|
表 4 各方案轨道拟合精度1D RMS及方案间差值 Tab. 4 1D RMS of orbit fitting accuracy of each scheme and their difference |
本文利用2021年doy180~195约120个测站数据,为保证框架与IGb 14对齐,采用北斗B1I/B3I频点数据和GPS L1/L2数据联合定轨,将相邻2 d弧段拟合残差的1D RMS值作为精密轨道精度的评价标准,分析不同北斗接收机天线相位中心改正模型的定轨性能,得到以下结论:
1) 对于接收机天线,同系统不同框架间的PCO差异较小,均未超过0.5 mm;而同一框架不同系统和频点间的PCO在U方向差异最大为3.38 mm。
2) 对于北斗二号,采用IGb 14框架的GPS L1/L2改正代替方案精密定轨结果略优于采用IGb R3框架下接收机天线北斗系统标定值代替方案;对于北斗三号,采用IGb R3框架下接收机天线北斗系统标定值代替方案可以取得最好的精密定轨结果。北斗三号MEO卫星定轨结果最优,其结果更具参考性,因此推荐在缺少接收机天线北斗PCC标定值时进行IGb 14框架下北斗系统精密数据处理中,选取IGb R3框架下接收机天线的北斗PCC标定值进行改正。接收机天线PCC赋0方案中,MEO卫星的定轨结果最差,表明接收机天线PCC对MEO卫星定轨的影响大于对IGSO卫星定轨的影响。
3) 当GPS与北斗双系统联合解算时,GPS和北斗系统轨道的参考框架以及接收机钟差等公共参数紧约束至GPS解,接收机天线北斗PCC误差则被更多传递到北斗轨道中。北斗单系统精密定轨中接收机天线北斗PCC误差更容易被接收机钟差等参数吸收,因此,接收机PCC赋0时北斗单系统精密定轨精度显著优于GPS与北斗双系统联合定轨,但由于仍存在较多模型误差,其定轨精度仍然较差。
本文选取IGb R3标定值代替和IGb 14框架GPS标定值代替均与IGb 14框架下接收机天线北斗PCC理论值存在差异。为保障多GNSS系统联合数据处理中框架的一致性,IGb 14框架下接收机北斗系统PCC模型仍需标定。
| [1] |
Johnston G, Riddell A, Hausler G. The International GNSS Service[A]//Teunissen P, Montenbruck O. SpringerHandbook of Global Navigation Satellite Systems[M]. New York: Springer, 2017
(  0) 0) |
| [2] |
刘洋洋, 许长辉, 庞辉, 等. 接收机天线相位中心改正对IGS/IGMAS站的影响[J]. 测绘科学, 2019, 44(5): 21-26 (Liu Yangyang, Xu Changhui, Pang Hui, et al. Analysis of Influence of Phase Correction of Receiver Antenna on IGS/IGMAS Station[J]. Science of Surveying and Mapping, 2019, 44(5): 21-26)
(  0) 0) |
| [3] |
王嘉琛, 刘根友, 郭爱智, 等. BDS接收机天线相位中心标定[J]. 测绘学报, 2020, 49(3): 312-321 (Wang Jiachen, Liu Genyou, Guo Aizhi, et al. BDS Receiver Antenna Phase Center Calibration[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(3): 312-321)
(  0) 0) |
| [4] |
张勤, 燕兴元, 黄观文, 等. 北斗卫星天线相位中心改正模型精化及对精密定轨和定位影响分析[J]. 测绘学报, 2020, 49(9): 1-1 111 (Zhang Qin, Yan Xingyuan, Huang Guanwen, et al. Refinement of BeiDou Satellite Antenna Phase Center Correction Model and Its Impact on Precision Orbit Determination and Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1-1 111)
(  0) 0) |
| [5] |
黄功文, 王小瑞, 党引群, 等. GNSS接收机天线相位中心改正对高精度定位影响[J]. 全球定位系统, 2014, 39(2): 49-53 (Huang Gongwen, Wang Xiaorui, Dang Yinqun, et al. Influence GNSS Receiver Antenna Phase Center Corrections on Precise Positioning[J]. GNSS World of China, 2014, 39(2): 49-53)
(  0) 0) |
| [6] |
Dilssner F, Springer T, Schönemann E, et al. Estimation of Satellite Antenna Phase Center Corrections for Beidou[C]. International GNSS Service Workshop 2014, Pasadena, USA, 2014
(  0) 0) |
| [7] |
Dach R, Schmid R, Schmitz M, et al. Improved Antenna Phase Center Models for GLONASS[J]. GPS Solutions, 2011, 15(1): 49-65 DOI:10.1007/s10291-010-0169-5
(  0) 0) |
| [8] |
Qu Z Y, Guo J, Zhao Q L. Phase Center Corrections for BDS IGSO and MEO Satellites in IGb14 and IGSR3 Frame[J]. Remote Sensing, 2021, 13(4)
(  0) 0) |
| [9] |
Yan X Y, Huang G W, Zhang Q, et al. Estimation of the Antenna Phase Center Correction Model for the BeiDou-3 MEO Satellites[J]. Remote Sensing, 2019, 11(23)
(  0) 0) |
| [10] |
Araszkiewicz A, Völksen C. The Impact of the Antenna Phase Center Models on the Coordinates in the EUREF Permanent Network[J]. GPS Solutions, 2017, 21(2): 747-757 DOI:10.1007/s10291-016-0564-7
(  0) 0) |
| [11] |
Xia F Y, Ye S R, Chen D Z, et al. Estimation of Antenna Phase Center Offsets for BeiDou IGSO and MEO Satellites[J]. GPS Solutions, 2020, 24(4)
(  0) 0) |
| [12] |
胡新乔, 刘万科, 刘晓磊, 等. 北斗天线相位中心改正策略及其对定位精度的影响分析[J]. 大地测量与地球动力学, 2018, 38(11): 1 137-1 142 (Hu Xinqiao, Liu Wanke, Liu Xiaolei, et al. Approach to BDS Antenna Phase Center Correction and Its Influences on Positioning[J]. Journal of Geodesy and Geodynamics, 2018, 38(11): 1 137-1 142)
(  0) 0) |
| [13] |
Huang G W, Yan X Y, Zhang Q, et al. Estimation of Antenna Phase Center Offset for BDS IGSO and MEO Satellites[J]. GPS Solutions, 2018, 22(2)
(  0) 0) |
| [14] |
胡志刚, 赵齐乐, 李陶, 等. 一种基于精密机械臂的室外GNSS接收机绝对天线相位中心校正方法: ZL201410780992.4[P]. 2015-04-08 (Hu Zhigang, Zhao Qile, Li Tao, et al. A Method of Absolute Antenna Phase Center Correction for Outdoor GNSS Receivers Based on Precision Mechanical Arm: 201410780992.4[P]. 2015-04-08)
(  0) 0) |
| [15] |
江峻毅, 尹潇, 李东, 等. 接收机天线相位中心改正对Galileo定位精度的影响分析[J]. 测绘工程, 2021, 30(1): 14-19 (Jiang Junyi, Yin Xiao, Li Dong, et al. Analysis of Receiver Antenna Phase Center Correction on Galileo Positioning[J]. Engineering of Surveying and Mapping, 2021, 30(1): 14-19)
(  0) 0) |
| [16] |
张磊, 兰孝奇, 房成贺, 等. 天线相位中心改正对GPS精密单点定位的影响[J]. 测绘工程, 2018, 27(3): 35-38 (Zhang Lei, Lan Xiaoqi, Fang Chenghe, et al. Impacts of the Antenna Phase Center Offset and Variant on GPS Positioning[J]. Engineering of Surveying and Mapping, 2018, 27(3): 35-38)
(  0) 0) |
| [17] |
张小红, 李星星, 郭斐. GNSS精密单点定位理论方法及其应用[M]. 北京: 国防工业出版社, 2021 (Zhang Xiaohong, Li Xingxing, Guo Fei. GNSS Precise Point Positioning Theory, Methods and Applications[M]. Beijing: National Defense Industry Press, 2021)
(  0) 0) |
| [18] |
苏牡丹, 赵齐乐, 郭靖, 等. 接收机端天线相位中心标定及其对北斗导航卫星精密定轨的影响[J]. 测绘学报, 2018, 47(增1): 78-85 (Su Mudan, Zhao Qile, Guo Jing, et al. Phase Center Calibration for Receiver Antenna and Its Impact on Precise Orbit Determination of BDS Satellites[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(S1): 78-85)
(  0) 0) |
| [19] |
马德强. GNSS接收机天线相位中心误差改正方法研究[D]. 西安: 长安大学, 2014 (Ma Deqiang. Study on the Correction Method of GNSS Receiver Antenna Phase Center Error[D]. Xi'an: Chang'an University, 2014)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


