2. 地理信息工程国家重点实验室,西安市雁塔路中段1号,710054
GRACE型卫星双星Z轴不对地定向,而是偏离径向约1°,用以实现双星严格互瞄。由于其主载荷星间测距仪(K-band ranging assembly,KBR)相位中心、星敏感器安装矩阵在卫星入轨后发生变化,可能导致星间指向出现系统性偏差,该偏差可通过星间指向定标进行确定,并上注(GRACE卫星仅在2003年上注)至卫星姿轨控系统[1-2],以实现准确的星间指向。星间指向性能评估可以监视星间指向状态,评估卫星姿控性能,辅助评估载荷状态,识别卫星机动事件。
Bandikova等[3]的研究表明,星间指向角定标参数的确定有在轨和地面两条实现途径:对于星间指向定标来说,一般通过在轨途径; 对于星间指向监视与评估,一般通过地面途径。然而,其并未给出在轨路径的实现策略。
GRACE-FO双星必须维持严格的星间指向,以保证其主载荷KBR和实验载荷卫星激光测距系统(the laser ranging interferometer,LRI)正常工作。尽管KBR在星间指向偏差达到4°时仍能进行观测,但必将导致较大的多路径效应。GRACE-FO星间指向角的设计指标为俯仰角(pitch)和偏航角(yaw)方向1 mrad、横滚角(roll)方向10 mrad,由姿轨控冷气推进系统和磁力矩器联合实现该姿控要求,其deadband一般设置为3~5 mrad[3]。LRI对星间指向要求更为严格,为了补偿星间指向常偏,通过差分波前传感技术测量本地信号波与接收波前之差,将其从数值控制回路返回给快速转动镜,以补偿卫星姿态抖动[4]。Goswami等[5]通过快速转动镜的输入数据获取卫星pitch和yaw方向的星间指向角,可作为评估星间指向角的一种备选方法。而在卫星间双向激光信号捕获过程中,为了完成星间激光链路的构建,需要维持星间指向角在0.04 mrad(3σ)以内[6],且持续36 h。
为研究GRACE型卫星星间指向定标算法,评估星间指向性能,本文推导了一种基于在轨路径,利用下传遥测数据计算星间指向定标参数的算法,给出定标实现策略,并利用GRACE-FO实测数据,基于地面路径对卫星星间指向性能进行评估。
1 GRACE型卫星星间指向维持策略GRACE-FO卫星姿轨控系统配备有12个10 mN的姿控推力器和2个50 mN的轨控推力器,同时,卫星每轴配备有磁偶极矩为27.5 mA2的磁力矩器作为主要的姿控器件。磁力矩器(magnetic torque,MTQ)三轴与卫星星体三轴平行安装,三轴磁力矩棒由圆柱形芯体和2个线圈组成。通过对指定轴向施加电流,能够产生该方向的磁力偶m,当与地球磁场B产生相互作用时,便能产生所需磁力矩T=m×B。为了实现双星互瞄,卫星需获得目标姿态,A星通过调整自身姿态至目标姿态,使得卫星KBR天线相位中心指向B星;B星以同样方式指向A星。由于A、B星之间无数据链路,因此无法获得对方的位置,必须从地面上传A、B星两行根数至双星,通过星上轨道预报计算对方星的位置,同时计算卫星视线方向(LOS,line-of-sight)连线作为目标姿态,通过姿轨控系统使得卫星姿态与视线方向一致。
为了获得高精度的星间指向,GRACE-FO卫星在通过两行根数计算目标姿态角时,采用Schlepp等[6]提出的基于自身GPS实时定轨结果修正星间指向的策略。而当进行LRI激光信号捕获时,需采用地面精密定轨结果,拟合上述GPS修正的星间相对位置,获得拟合参数,并与两行根数同步上注,以获得最高精度的星间指向结果。
当卫星KBR相位中心或星敏(star camera assembly,SCA)安装矩阵更新后,需要对星间指向定标参数进行更新。在GRACE卫星中,将SCA至星间指向的旋转矩阵定义为QKS1B,在GRACE-FO中定义为QCP1B[7]。相关参数及含义见表 1。
|
|
表 1 星间指向相关的1B级数据 Tab. 1 Level-1B data related to inter-satellite pointing |
将K-Frame(KBR天线相位中心框架)到LOS-Frame(卫星视线参考框架)的方向余弦矩阵定义为星间指向方向余弦矩阵RKF→LOS,将其转换为欧拉角的形式:
| $ \boldsymbol{R}_{\mathrm{KF} \rightarrow \mathrm{LOS}}=\boldsymbol{R}_x(\psi) \boldsymbol{R}_y(\theta) \boldsymbol{R}_z(\varphi) $ | (1) |
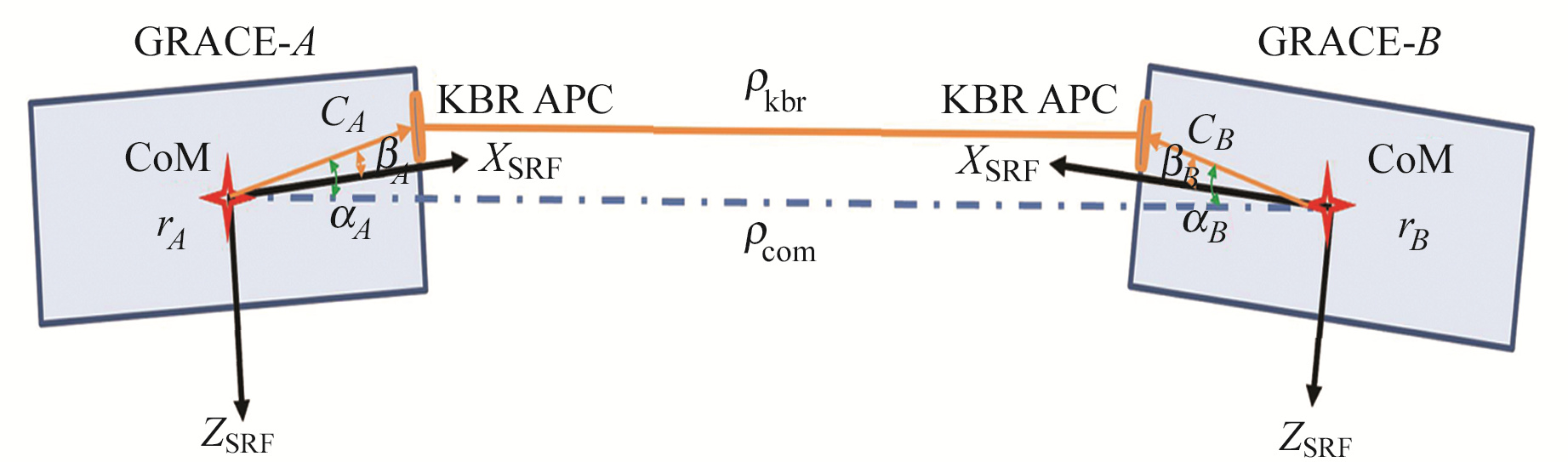
式中,ψ为绕x轴的横滚角(roll),θ为绕y轴的俯仰角(pitch),φ为绕z轴的偏航角(yaw)。在图 1中,用立体角αA和αB分别表示A、B星的pitch和yaw方向的星间指向角之和,用立体角βA和βB分别表示A、B星的KBR天线相位中心(antenna phase center,APC)在科学坐标系下的指向角。
|
图 1 GRACE型卫星星间指向角示意图 Fig. 1 Diagram of inter-satellite pointing angle of GRACE satellite |
由欧拉角ψ、θ、φ计算方向余弦矩阵RKF→LOS的公式为:
| $ \begin{aligned} & \boldsymbol{R}_{\mathrm{KF} \rightarrow \mathrm{LOS}}=\left[\begin{array}{c} \cos \theta \cos \varphi \\ -\cos \psi \sin \varphi+\sin \psi \sin \theta \cos \varphi \\ \sin \psi \sin \varphi+\cos \psi \sin \theta \cos \varphi \end{array}\right. \\ & \left.\begin{array}{cc} \cos \theta \sin \varphi & -\sin \theta \\ \cos \psi \cos \varphi+\sin \psi \sin \theta \sin \varphi & \sin \psi \cos \theta \\ -\sin \psi \cos \varphi+\cos \psi \sin \theta \sin \varphi & \cos \psi \cos \theta \end{array}\right] \\ & \end{aligned} $ | (2) |
反之,由方向余弦矩阵计算欧拉角的公式为:
| $ \left\{\begin{array}{l} \psi=-\arctan \left(\frac{R_{23}}{R_{33}}\right) \\ \theta=\arcsin \left(R_{13}\right) \\ \varphi=-\arctan \left(\frac{R_{12}}{R_{11}}\right) \end{array}\right. $ | (3) |
式中,Rij是RKF→LOS矩阵的各个元素。
2.2 在轨路径星间指向定标姿轨控系统星间指向维持依据的是在轨预报的卫星位置和在轨实时测量的卫星姿态,因此,一般依据在轨路径进行星间指向定标。可依据事后地面路径获得的1B级数据计算准确的星间指向,用于评估其性能。2条路径的计算流程如图 2所示。

|
图 2 星间指向角计算的2种方法 Fig. 2 Two methods for calculating the inter-satellite pointing angle |
在轨路径的星间指向计算公式为:
| $ \boldsymbol{R}_{\mathrm{KF} \rightarrow \mathrm{LOS}}=\boldsymbol{R}_{\text {iner } \rightarrow \mathrm{LOS}} \cdot\left(\boldsymbol{R}_{\text {iner } \rightarrow \mathrm{SCF}}\right)^{\mathrm{T}} \cdot\left(\boldsymbol{R}_{\mathrm{SCF} \rightarrow \mathrm{KF}}\right)^{\mathrm{T}} $ | (4) |
式中,Riner→LOS为惯性系到视线参考坐标系的转换矩阵,其卫星位置由星上轨道积分器基于两行根数TLE获取,通过遥测数据下传; Riner→SCF为惯性系转换到星敏框架的转换矩阵,由星上定姿解算获得,通过遥测数据下传; RSCF→KF为星敏框架转换到KBR相位中心参考框架的转换矩阵,由星敏感器和KBR相位中心矢量安装矩阵给出,将其转换为四元数形式,即为星间指向定标参数QKS1B。
基于在轨路径计算星间指向角需要从遥测数据中获取轨道预报和实时姿态测量数据,根据式(4)进行计算。因此,反算星间指向定标参数QKS1B亦需要获取遥测参数中的相关数据,而一般用户难以获得该数据。故本文仅对计算QKS1B的相关公式进行推导,不进行实测数据验证。
通过计算数天的RKF→LOS,可以获得旋转欧拉角的平均值。若roll方向平均值偏离超过10 mrad,或者pitch和yaw方向超过1 mrad,则需要对RSCF→KF进行修正,以获得新的RSCF→KF定标参数,使得RKF→LOS的均值趋于0。
依据在轨路径的星间指向定标主要步骤如下:
1) 通过式(4)计算自上次QKS1B更新以来的星间指向角方向余弦矩阵RKF→LOS,选取数据时排除质心定标机动、KBR定标机动等大的姿态机动等事件影响段全天的数据;
2) 通过式(3)计算对应的欧拉角,并计算欧拉角的均值ψ0、θ0、φ0;
3) 通过式(2)计算QKS1B的修正矩阵RΔQKS=Rx(-ψ0)Ry(-θ0)Rz(-φ0);
4) 计算新的QKS1B方向余弦矩阵RQKS1B=RSCF→KF·R TΔQKS1B;
4) 将RQKS1B转换为四元数形式,得到更新后的QKS1B,上注至卫星姿轨控分系统。
2.3 地面路径星间指向精度评估地面路径的星间指向计算公式为:
| $ \boldsymbol{R}_{\mathrm{KF} \rightarrow \mathrm{LOS}}=\boldsymbol{R}_{\text {iner } \rightarrow \mathrm{LOS}} \cdot\left(\boldsymbol{R}_{\text {iner } \rightarrow \mathrm{KF}}\right)^{\mathrm{T}} $ | (5) |
其中,
| $ \boldsymbol{R}_{\text {iner } \rightarrow \mathrm{KF}}=\left[\begin{array}{c} \boldsymbol{R}_{\mathrm{SRF} \rightarrow \text { iner }} \frac{\mathrm{pc}}{|\mathrm{pc}|} \\ \boldsymbol{Z}_{\mathrm{KF}} \times \boldsymbol{X}_{\mathrm{KF}} \\ \boldsymbol{X}_{\mathrm{KF}} \times \boldsymbol{y}_{\mathrm{SRF}} \end{array}\right] $ | (6) |
式中,pc从VKB1B中获取,则
对比式(4)和式(5),Riner→LOS由惯性系下的双星位置确定,在轨路径时依赖星上预报轨道,地面路径时则采用GNI1B数据,可以得到:
| $ \boldsymbol{R}_{\text {iner } \rightarrow \mathrm{LOS}}=\left[\begin{array}{c} \frac{r_i-r_j}{\left|r_i-r_j\right|} \\ x_{\mathrm{LOS}_j} \times \frac{r_A}{\left|r_A\right|} \\ x_{\mathrm{LOS}_j} \times y_{\mathrm{LOS}_j} \end{array}\right] $ | (7) |
式中,i、j=A、B,r为卫星在惯性系下的位置。
3 GRACE-FO卫星星间指向性能评估使用2018-06-01~2022-06-23的1B级GRACE-FO实测数据,基于地面路径对星间指向性能进行评估。
3.1 星间指向精度评估为评估2018-06-01以来的星间指向角精度,依据轨道平面与太阳位置夹角(β角)周期322 d,分别统计C、D卫星星间指向情况。β角计算公式为:
| $ \beta=\arccos \left(\frac{n \cdot r_{\odot}}{|n| \cdot r_{\odot}}\right)-90^{\circ} $ | (8) |
式中,n为卫星轨道面法线,r⊙为日地连线。因此,当日地连线与卫星轨道面法线平行时,β角为±90°,此时卫星光照最强。
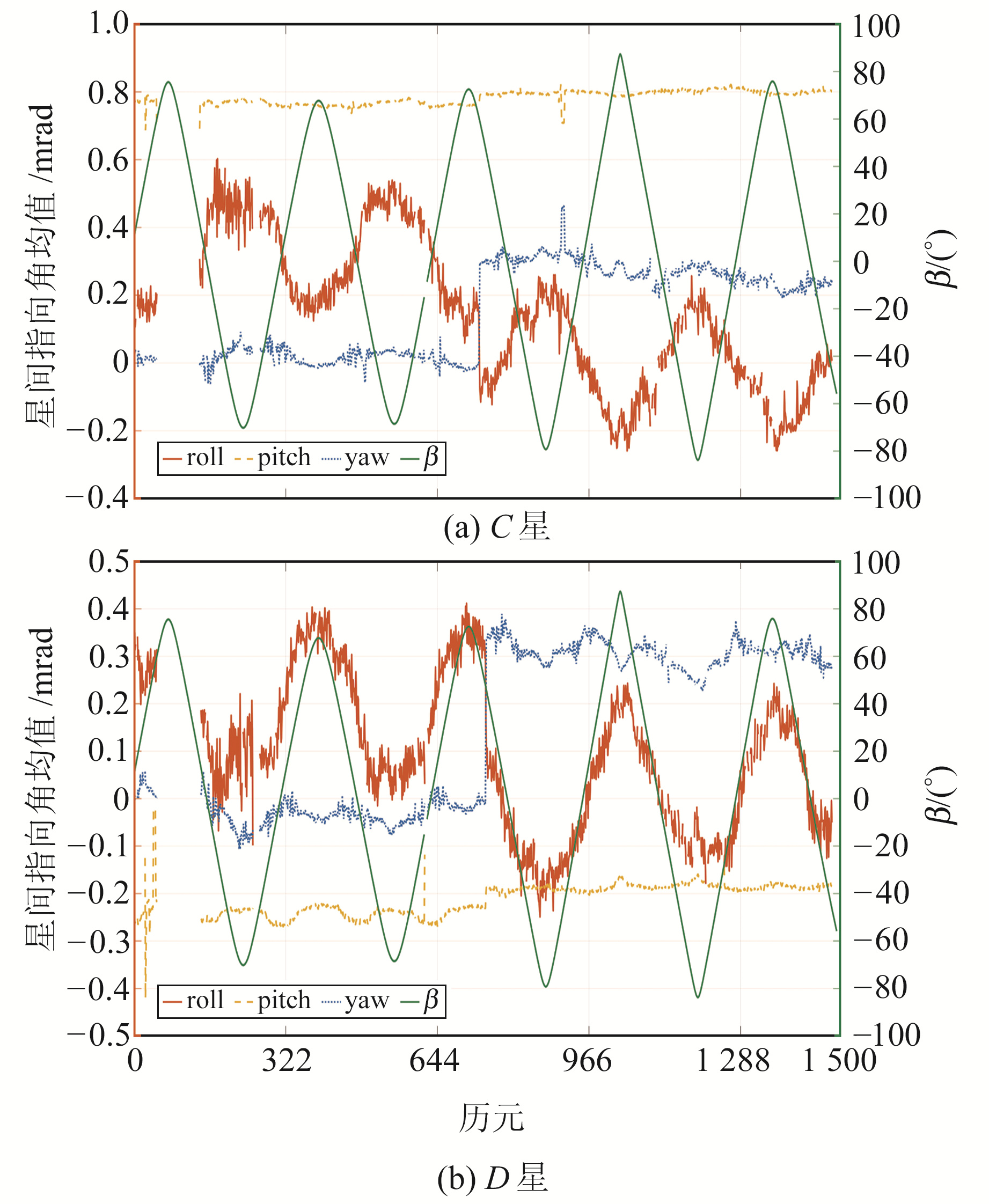
图 3显示2018-06-01以来每天的星间指向角均值曲线,可以看出,C星星间指向角pitch方向均值约为0.8 mrad、yaw方向由0左右上升到0.25 mrad左右;D星星间指向角pitch方向均值由-0.25 mrad左右上升至-0.2 mrad左右、yaw方向由0左右上升到0.3 mrad左右。C、D星的roll方向指向角与β角有很强的相关性,而β角反映卫星所受光照条件,所以二者的相关性可能源于星敏定姿结果存在随温度变化的系统差。C星星间指向角跳变的日期为2020-06-02,D星为2020-06-16。查阅JPL公布的卫星事件文件TN-01a_SCE可知,C星于2020-06-02更新了星敏2、3安装矩阵(QSA1B)。
|
图 3 GRACE-FO卫星2018-06-01~2022-06-23期间星间指向角均值 Fig. 3 The mean value of inter-satellite pointing angle of GRACE-FO from 2018-06-01 to 2022-06-23 |
事实上,图 3中的均值曲线去掉了受卫星事件影响的天数。例如,统计天数为1 484 d,C星曲线中仅显示1 264 d,D星曲线中仅显示1 253 d,有89 d因为D星GPS数据中断无法计算星间指向角; 其余天包含的卫星事件有质心定标机动、切换到对地指向模式(nadir pointing)、KBR定标机动、切换到安全模式[8](acquisition and safe mode,ASM)、推力器校正实验、轨道控制、防碰撞机动、C星yaw turn机动(yaw方向指向角切换到180°)等。卫星事件会导致星间指向角标准差变大,因此可以通过星间指向角的单日标准差STD进行自动判断。当roll标准差大于1.4 mrad、pitch大于0.4 mrad或yaw大于1.4 mrad时,即认为当天含有影响星间指向角精度的卫星事件。典型卫星事件,如质心定标机动可以参考文献[9]中相关星间指向情况,KBR定标机动可以参考文献[10]中相关星间指向情况。
按照β角周期,对1 484 d的星间指向角标准差进行统计(去掉影响星间指向精度评估的卫星事件),如表 2所示。
|
|
表 2 自发射以来的星间指向角标准差 Tab. 2 The standard deviation of the inter-satellite pointing since launch |
可以看出,按照各个周期统计获得的星间指向角标准差较为一致,且与全部1 484 d的统计结果较为一致。
绘制2018-06-01以来每天的星间指向角标准差曲线(图 4),可以看出,标准差并未受到β角周期的影响,表明β角仅带来roll方向星间指向角系统差,并不影响roll方向星间指向角精度。而C、D星roll方向星间指向角精度在2018-11-15~2019-02-06期间明显变大,查阅TN-01a_SCE可知,在2018-11-15上注了新的姿轨控系统精细指向(fine pointing,FP)控制参数,而恢复原参数的时间并未记录。其中,C星pitch方向在2021-06-01开始对地定向实验后,仍有部分机动影响时段并未完全消除,但量级较小。

|
图 4 GRACE-FO卫星2018-06-01~2022-06-23的星间指向角标准差 Fig. 4 The STD of inter-satellite pointing angle of GRACE-FO from 2018-06-01 to 2022-06-23 |
星间指向角RMS在roll方向应小于10 mrad、在pitch和yaw方向应小于1 mrad,为此,绘制去除影响星间指向角卫星事件后的星间指向角RMS(图 5)。显然,自发射以来,星间指向角满足性能指标要求。

|
图 5 GRACE-FO卫星2018-06-01~2022-06-23的星间指向角RMS Fig. 5 The RMS of inter-satellite pointing angle of GRACE-FO from 2018-06-01 to 2022-06-23 |
卫星姿控系统主要依靠姿控推力器和磁力矩器,联合实现对卫星的姿态控制。为了评估其姿控性能,选取2021-11-04~21的MAG1B数据,绘制该段时间内的C星星间指向角RMS和磁场强度经纬度分布(图 6)。

|
图 6 C星2021-11-04~21的星间指向角RMS和磁场强度 Fig. 6 The RMS of inter-satellite pointing angle of GRACE-C from 2021-11-04 to 2021-11-21 and magnetic field strength |
由图 6(a)可见,星间指向角精度与地磁场分布强相关,roll方向星间指向角在地磁赤道处精度较好; pitch方向星间指向角在全部区域存在明显常偏,但其波动最小,在0.70~0.95 mrad之间,仅在南大西洋磁异常区精度稍差; yaw方向星间指向角在地磁赤道和南大西洋磁异常区精度较差。由图 6(b)可见,磁强计测量精度较为一致,可以为磁力矩器工作提供较好的磁场强度测量数据。
根据T=m×B,地球磁场B在某纬度单方向的磁场强度及期望的力矩方向决定了磁力偶m的通电电流方向。参考图 6(b)磁场强度分布,可以推断磁力矩器在不同纬度工作时的磁力矩器轴通电情况和姿态控制能力(表 3)。选取2021-11-04~21的THR1B数据,将C、D星推力器点火事件按照经纬度分布情况绘制(图 7),可以看出,C、D星推力器点火的经纬度分布规律较为一致,roll推力器点火集中在赤道附近,pitch点火事件极为稀少,yaw推力器点火分布在高纬度区域,且符合表 3所推测的情况。图 6和图 7显示出姿轨控系统磁力矩和姿控推力器能够配合实现姿控要求。
|
|
表 3 磁力矩器在不同纬度的姿控能力 Tab. 3 The attitude control ability of magnetic torquer at different latitudes |

|
图 7 GRACE-FO卫星2021-11-04~21的姿控点火事件 Fig. 7 The thruster events of GRACE-FO from 2021-11-04 to 2021-11-21 |
1) 基于地面路径的星间指向评估能够识别星间指向角常偏,对星间指向定标有借鉴意义。
2) 2020-06-02C星的2、3星敏安装矩阵(QSA1B)更新后,星间指向角常偏略微变大。
3) roll方向星间指向角均值与β角有强相关性。
4) 从星间指向角统计的标准差和RMS可以看出,GRACE-FO卫星的星间指向满足要求,保证了KBR正常工作所需的基本条件。
5) GRACE-FO卫星姿轨控系统的磁力矩和姿控推力器能够配合完成姿控需求。
| [1] |
Kornfeld, R P, Arnold, B W, Gross, M A, et al. GRACE-FO: The Gravity Recovery and Climate Experiment Follow-On Mission[J]. Journal of Spacecraft and Rockets, 2019, 56(3): 931-951 DOI:10.2514/1.A34326
(  0) 0) |
| [2] |
Bandikova T. The Role of Attitude Determination for Inter-Satellite Ranging[D]. Hannover: Leibniz University of Hannover, 2015
(  0) 0) |
| [3] |
Bandikova T, Flury J, Ko U D. Characteristics and Accuracies of the GRACE Inter-Satellite Pointing[J]. Advances in Space Research, 2012, 50(1): 123-135 DOI:10.1016/j.asr.2012.03.011
(  0) 0) |
| [4] |
闫易浩. GRACE/GRACE-FO重力卫星星间测距系统数据处理关键技术研究[D]. 武汉: 华中科技大学, 2021 (Yan Yihao. Research on the Raw Data Processing Technology of the Inter-Satellite Ranging System of GRACE/GRACE-FO Gravimetric Missions[D]. Whuhan: Huazhong University of Science and Technology, 2021))
(  0) 0) |
| [5] |
Goswami S, Francis S P, Bandikova T, et al. Analysis of GRACE Follow-On Laser Ranging Interferometer Derived Inter-Satellite Pointing Angles[J]. IEEE Sensors Journal, 2021, 21(17): 19 209-19 221 DOI:10.1109/JSEN.2021.3090790
(  0) 0) |
| [6] |
Schlepp B, Kirschner M, Sweetser T H, et al. Flight Dynamics Challenges for the GRACE Follow-On Mission[C]. 25th International Symposium on Space Flight Dynamics(ISSFD), Munich, 2015
(  0) 0) |
| [7] |
Wen H Y, Kruizinga G, Paik M, et al. Gravity Recovery and Climate Experiment Follow-On(GRACE-FO) Level-1 Data Product User Handbook; Technical Report JPL, D-56935[R]. NASA Jet Propulsion Laboratory/California Institute of Technology: Pasadena, 2019
(  0) 0) |
| [8] |
Cossavella F, Herman J, Hoffmann L, et al. Attitude Control on GRACE Follow-On: Experiences from the First Years in Orbit[M]. Cham: Springer, 2022
(  0) 0) |
| [9] |
Huang Z Y, Li S S, Cai L, et al. Estimation of the Center of Mass of GRACE-Type Gravity Satellites[J]. Remote Sensing, 2022(14): 4 030
(  0) 0) |
| [10] |
Huang Z Y, Li S S, Huang L Y, et al. On-Orbit Calibration of the KBR Antenna Phase Center of GRACE-Type Gravity Satellites[J]. Remote Sensing, 2022(14): 3 395
(  0) 0) |
2. State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi 'an 710054, China
 2023, Vol. 43
2023, Vol. 43


