2. 中国地震台网中心,北京市三里河南横街5号,100045
对于钻孔应变仪来说,除了要标定位移敏感元件外,还要标定由钢筒、固结水泥及围岩构成的轴对称结构。本文钻孔应变仪的标定特指对轴对称结构的标定。
位移敏感元件沿任意水平方向(用方位角θ表示)观测的钢筒内壁的线应变Sθ与所在区域的水平应变状态(用最大主应变ε1、最小主应变ε2和最大主应变方向的方位角φ表示)之间的关系为[1]:
| $ S=A\left(\varepsilon_1+\varepsilon_2\right)+B\left(\varepsilon_1-\varepsilon_2\right) \cos 2(\theta-\varphi) $ | (1) |
式中,A为面应变的灵敏系数;B为剪应变的灵敏系数。基于式(1),可由在钻孔应变仪钢筒内沿不同水平方向上安设的位移敏感元件(最少需要3个)观测的线应变计算出所在区域的水平应变状态(ε1,ε2,φ)。标定钻孔应变仪就是要确定A和B的值[2]。
钻孔应变仪的标定方法主要有2种:1)通过共同观测应变固体潮,用理论应变固体潮标定钻孔应变仪[3];2)通过共同观测远震面波,用地震仪标定钻孔应变仪[2]。但理论固体潮给出的不是台站所在地的实际观测值,没有真正解决钻孔应变仪的准确标定问题,而地震仪给出的是台站所在地的实际观测值。
邱泽华[2]应用Igel等[4]给出的瑞利面波的水平振动应变与水平振动速度之间的关系和勒夫面波的水平振动应变与水平振动速度之间的关系,将地震仪观测的瑞利波水平振动速度转换为水平振动应变,将地震仪观测的勒夫波水平振动速度转换为水平振动应变,从而使得地震仪与钻孔应变仪有了共同观测的对象——振动应变,奠定了用地震仪标定钻孔应变仪的基础。
应用上述方法,基于多个远震的面波标定仁和地震台的YRY-4型钻孔应变仪。结果发现,用不同的远震面波标定出的A值和B值差别较大。这是因为上述方法缺少标定的准确性评价,即评价A值和B值哪一个更准确。为此,本文以用地震仪准确标定钻孔应变仪为目标,在全面论述标定方法的基础上,重点解决标定的准确性评价问题,为钻孔应变仪的进一步应用,特别是与地震仪联合测震奠定基础。
1 原理与方法如果把钢筒内壁想象为无限薄的筒,那么安设在垂向钢筒内的位移敏感元件直接观测的实际上是钢筒内壁的水平正应变。式(1)实际上给出的是在任意方位θ上,钢筒内壁的水平正应变S(用水平面应变ε10+ε20、水平最大剪应变ε10-ε20和水平最大主应变ε10的方位角φ0表示)与钻孔应变仪所在区域的水平应变状态(用水平面应变ε1+ε2、水平最大剪应变ε1-ε2和水平最大主应变ε1的方位角φ表示)之间的理论关系。容易推得下面的公式:
| $ \varepsilon_1+\varepsilon_2=\frac{\varepsilon_1^0+\varepsilon_2^0}{2 A} $ | (2) |
| $ \varphi=\varphi^0 $ | (3) |
| $ \varepsilon_1-\varepsilon_2=\frac{\varepsilon_1^0-\varepsilon_2^0}{2 B} $ | (4) |
显然,可以由钢筒内壁的水平应变状态(ε10+ε20,ε10-ε20,φ0)通过2个需要标定的常数值A和B间接计算出所在区域的水平应变状态(ε1+ε2,ε1-ε2,φ)。因此,ε1+ε2、ε1-ε2和φ称为钻孔应变仪的间接输出量。
根据式(2)~(4)和瑞利波的波动一阶微分方程可以导出:
| $ \begin{gathered} \frac{v_R}{\alpha}=-\frac{\varepsilon_1^0+\varepsilon_2^0}{4 A}-\frac{\varepsilon_1^0-\varepsilon_2^0}{4 B} \cos 2\left(\theta-\varphi^0\right)= \\ -\frac{\varepsilon_1^0+\varepsilon_2^0}{4 A}-\frac{\lambda_{R T}^0}{4 B} \end{gathered} $ | (5) |
式中,λRT0=(ε10-ε20)cos2(θ-φ0)为钢筒内壁的径向差应变,υR为瑞利波径向振动速度。
式(5)就是用钢筒内壁的面应变ε10+ε20和径向差应变λRT0表示的瑞利波径向分量的波动一阶微分方程。
根据式(2)~(4)和勒夫波的波动一阶微分方程可以导出:
| $ \frac{v_T}{\beta}=\frac{\varepsilon_1^0-\varepsilon_2^0}{2 B} \sin 2\left(\theta-\varphi^0\right)=-\frac{\gamma_{R T}^0}{2 B} $ | (6) |
式中,γRT0=-(ε10-ε20)sin2(θ-φ0)为钢筒内壁的径向剪应变,υT为勒夫波切向振动速度
式(6)就是用钢筒内壁的径向剪应变γRT0表示的勒夫波的波动一阶微分方程。
瑞利波和勒夫波的走时曲线为直线,斜率不随震中距变化而变化[5],说明它们的传播速度(α和β)是恒定的,可作为已知值处理。因此,可以应用式(5)和式(6)标定A值和B值。考虑到式(5)中既包含A值又包含B值,而式(6)中只包含B值,因此,本文采取的标定策略是先用式(6)标定出B值,再用式(5)标定出A值。
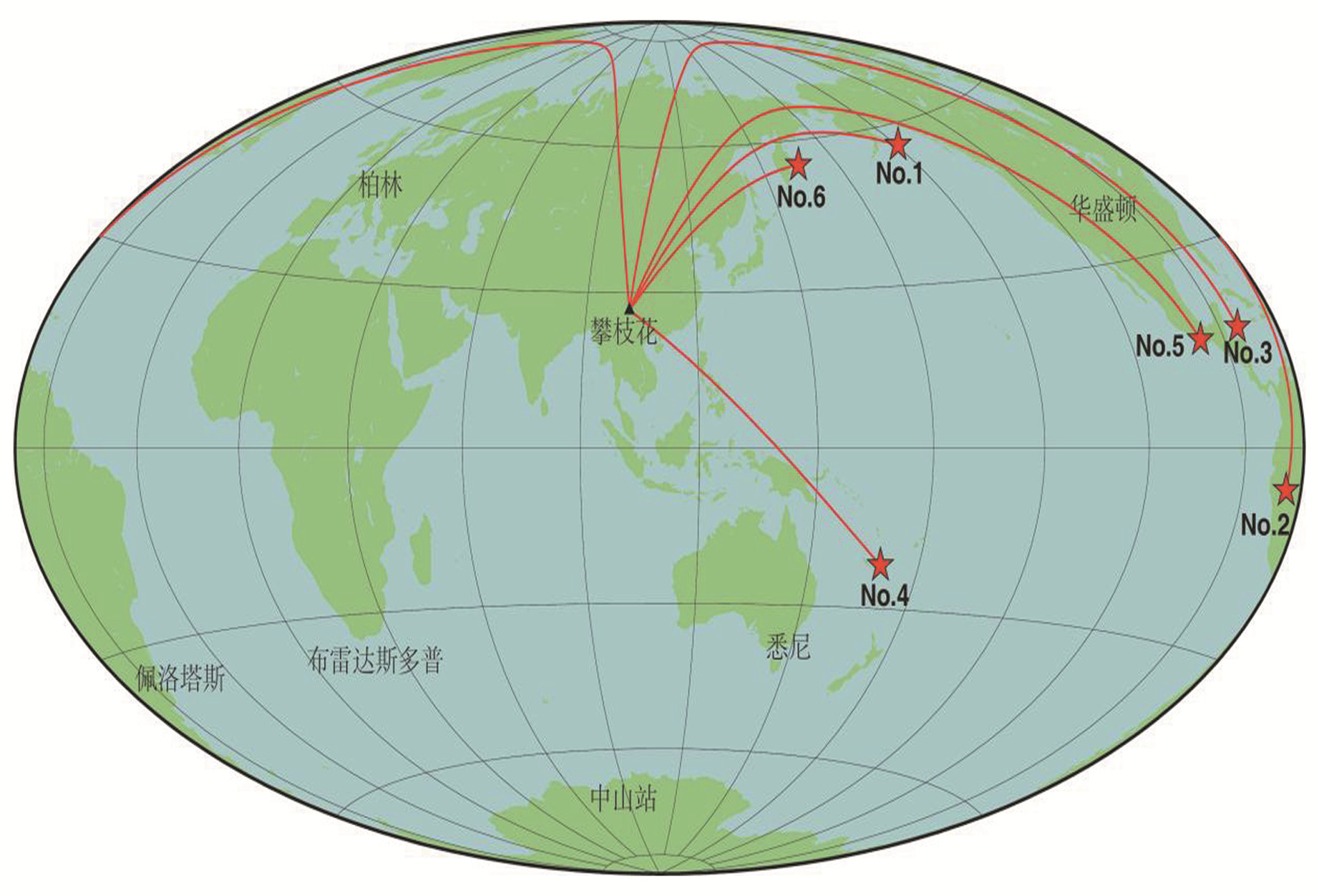
2 应用选择仁和台的钻孔应变仪验证本文标定方法。表 1列出了标定中用到的一些基本参数,其中,瑞利波和勒夫波的速度值来自文献[5]。表 2列出了标定用的6个震级较大的远震,其空间分布见图 1。根据震源的经纬度和台站的经纬度计算的6个地震的震中距Δ和地震射线的方位角θ见表 3。
|
|
表 1 基本参数 Tab. 1 Basic parameters |
|
|
表 2 地震基本信息 Tab. 2 Basic information of earthquakes |
|
图 1 仁和地震台及6个远震震中分布 Fig. 1 Distribution of epicenters of six teleseisms and Renhe seismic station |
|
|
表 3 仁和台钻孔应变仪的标定计算 Tab. 3 Calibration calculation of borehole strainmeter at Renhe station |
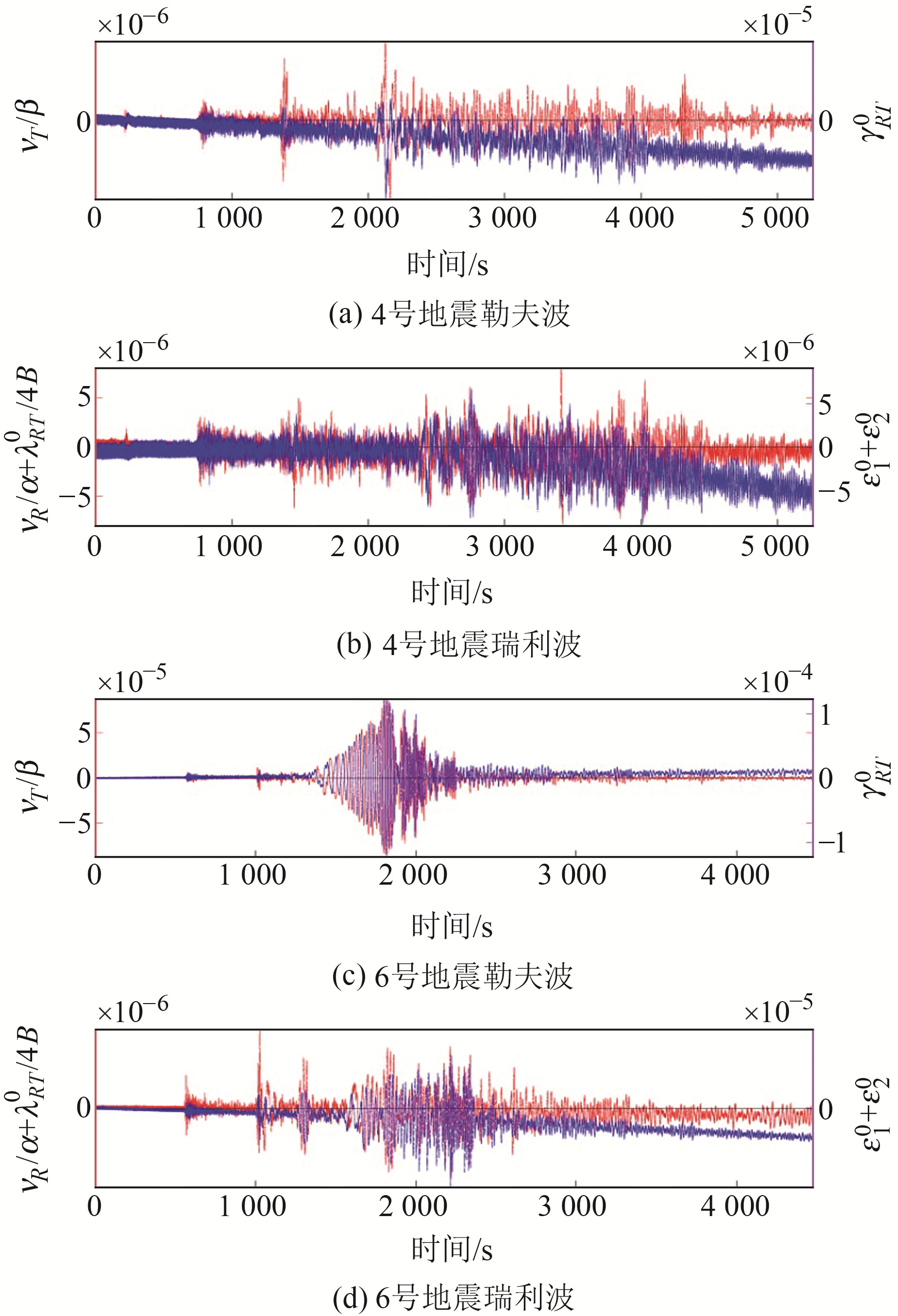
图 2(b)、2(d)展示了滤波前4号与6号地震的υR/α+λRT0/4B(红线)和ε10+ε20(蓝线)。可以看出,两者都存在明显的长周期变化和高频噪声。
|
图 2 滤波前勒夫波和瑞利波波形 Fig. 2 Love and Rayleigh waveforms before filtering |
图 2(a)、2(c)展示了滤波前4号与6号地震的υT/β(红线)和γRT0(蓝线)。可以看出,γRT0存在明显的长周期变化,υT/β和γRT0均存在高频噪声,但γRT0的高频噪声更大些。
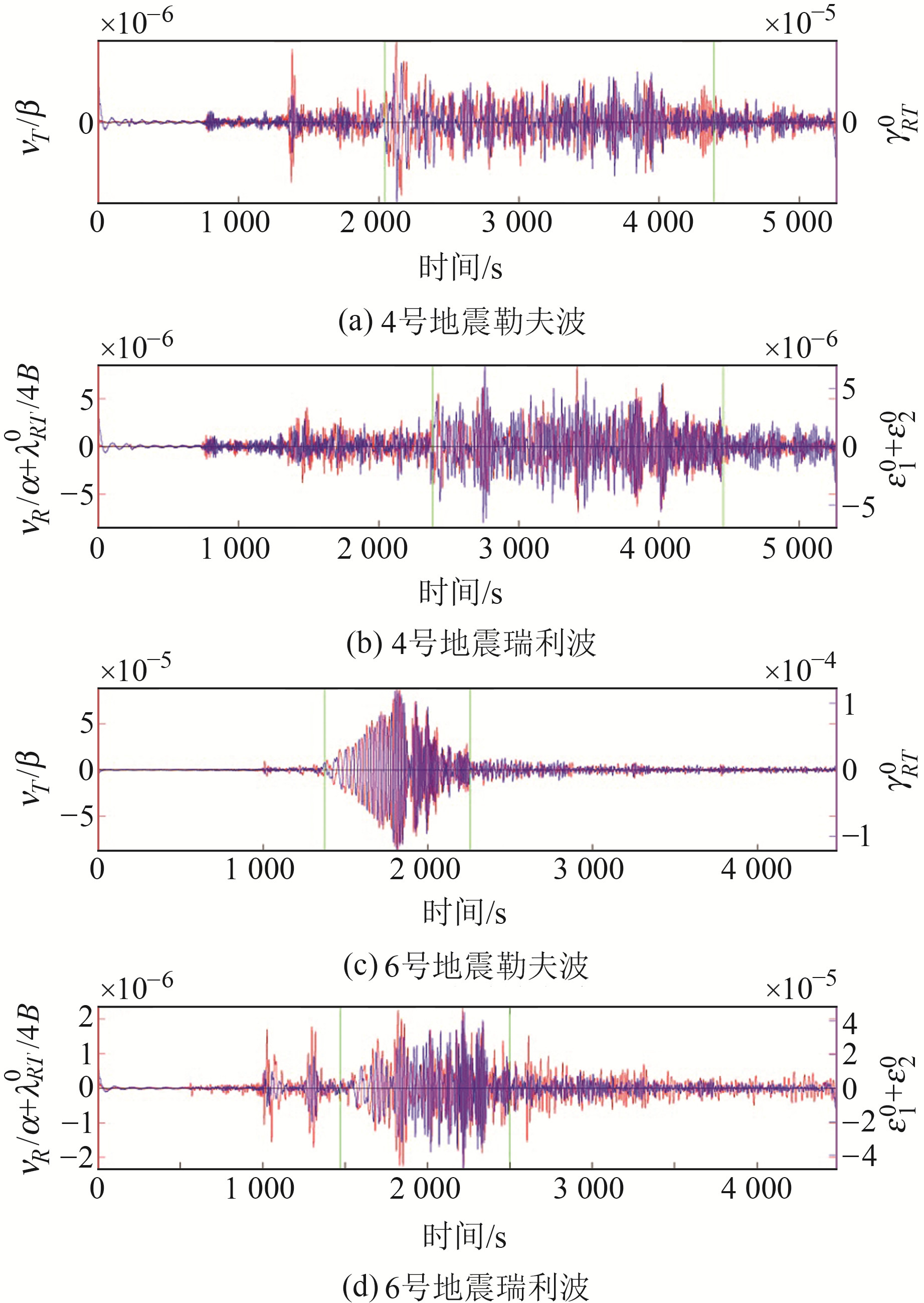
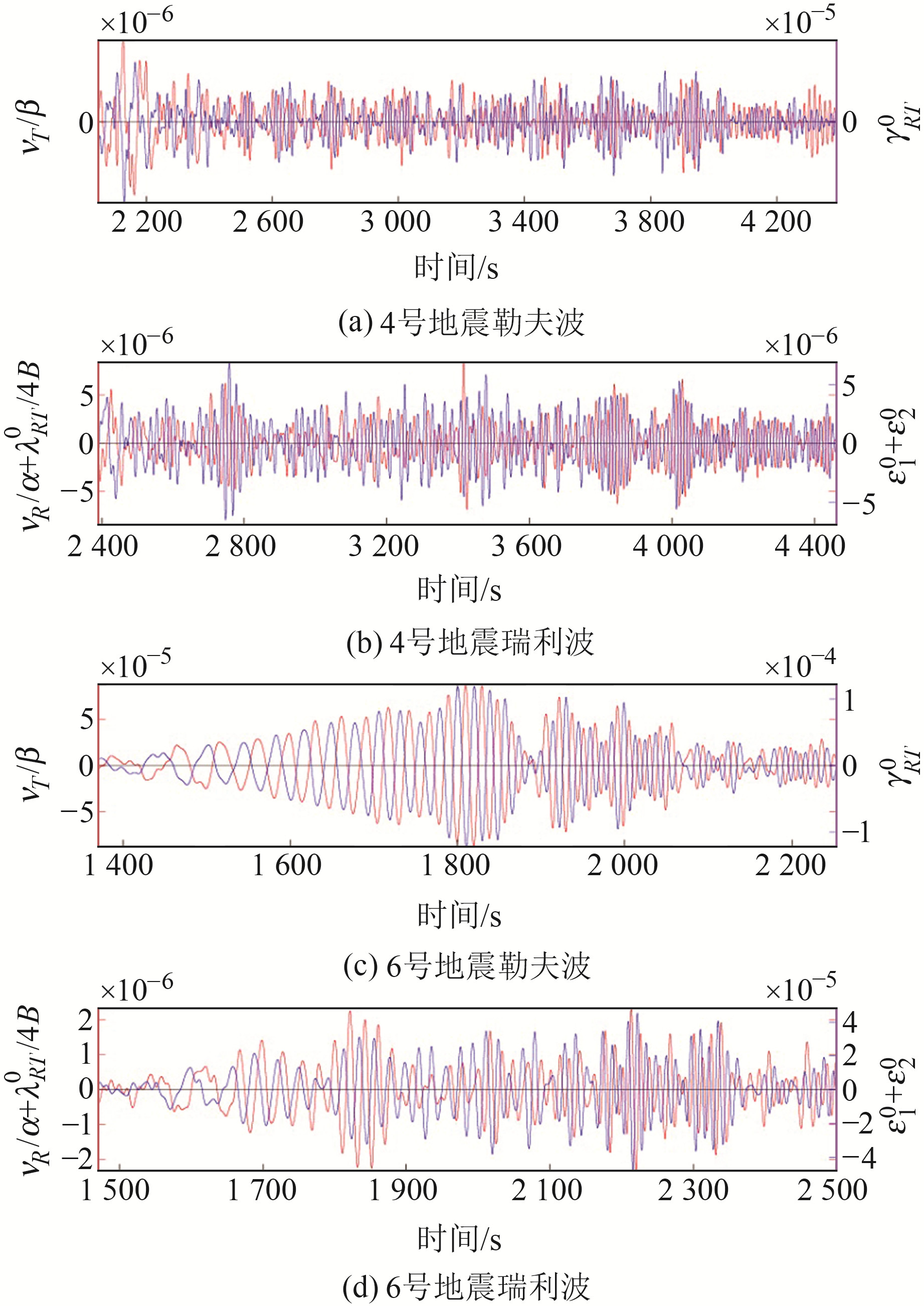
图 3(b)、3(d)为4号与6号地震滤波后的υR/α+λRT0/4B(红线)和ε10+ε20(蓝线)结果;图 3(a)、3(c)为4号与6号地震滤波后的υT/β(红线)和γRT0(蓝线)结果。图 3(b)、3(d)绿色线分别标示出了4号与6号地震的瑞利波起止范围,放大展示于图 4(b)、4(d);图 3(a)、3(c)绿色线分别标示出了4号与6号地震的勒夫波起止范围,放大展示于图 4(a)、4(c)。
|
图 3 滤波后勒夫波和瑞利波波形 Fig. 3 Love and Rayleigh waveforms after filtering |
|
图 4 根据标定结果绘制的勒夫波和瑞利波波形曲线 Fig. 4 Love and Rayleigh waveforms based on calibration results |
由式(2)可知,钢筒内壁的面应变与所在区域的面应变之比为2A,因此,面应变的灵敏系数为2A,而不是传统认识上的A。由式(3)、(4)可知,在任意方位θ上,钢筒内壁的剪应变γ0与所在区域的剪应变γ之比为2B,因此,2B为剪应变的灵敏系数,而不是传统认识上的B。
式(3)中,φ=φ0说明钢筒内壁的水平应变主轴与所在区域的水平应变主轴完全重合,即2个应变状态的结构完全相同,不同的只是数值的大小,钢筒内壁面应变是所在区域面应变的2A倍,钢筒内壁剪应变是所在区域剪应变的2B倍。因此,2A≥0、2B≥0,即A≥0、B≥0。当2A=0、2B=0,即A=0、B=0时,ε10+ε20=0、γ0=0,说明钢筒内壁不随区域发生形变。当2A=1、2B=1,即A=0.5、B=0.5时,ε10+ε20=ε1+ε2、γ0=γ,钢筒内壁的应变状态与所在区域的应变状态完全相同,可视作虚孔观测情形。
不同远震面波数据的信噪比不同,不同信噪比的数据能够准确标定出A值和B值的程度也不同,也就是说标定效度是不同的。标定效度越大,标定出的B值和A值就越准确。6个地震的B值和A值标定效度列于表 3。可以看到,6号地震的B值和4号地震的A值标定效度最接近-1,取其相应的B值和A值作为最终标定值。故仁和地震台钻孔应变仪的最终标定结果为A=0.36,B=0.73。
面应变的灵敏系数2A=0.72,说明钢筒内壁的面应变相比于所在区域的面应变缩小;最大剪应变的灵敏系数2B=1.46,说明钢筒内壁的剪应变相比于所在区域的剪应变放大。
由表 3还可以看到,6号地震的B值标定效度最接近-1,但其A值的标定效度离-1最远;4号地震的A值标定效度最接近-1,但其B值标定效度离-1最远,这可能是震源辐射方向性所致。由此可知,用一个地震难以同时标定好A值和B值。
致谢: 感谢苏凯之研究员和薛兵研究员提供的帮助。
| [1] |
潘立宙. 测量地应力的钻孔变形法[C]//地应力测量的原理和应用. 北京: 地质出版社, 1981 (Pan Lizhou. Borehole Deformation Method for Measuring In-Situ Stress[C]//Principles and Applications of Ground Stress Measurement. Beijing: Geological Publishing House, 1981)
(  0) 0) |
| [2] |
邱泽华. 钻孔应变观测理论与应用[M]. 北京: 地震出版社, 2017 (Qiu Zehua. Borehole Strain Observation: Theory and Application[M]. Beijing: Seismological Press, 2017)
(  0) 0) |
| [3] |
Qiu Z H, Tang L, Zhang B H, et al. In Situ Calibration of and Algorithm for Strain Monitoring Using Four-Gauge Borehole Strainmeters(FGBS)[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(4): 1 609-1 618
(  0) 0) |
| [4] |
Igel H, Schreiber U, Flaws A, et al. Rotational Motions Induced by the M8.1 Tokachi-Oki Earthquake, September 25, 2003[J]. Geophysical Research Letters, 2005, 32(8)
(  0) 0) |
| [5] |
Shearer P M. Imaging Global Body Wave Phases by Stacking Long-Period Seismograms[J]. Journal of Geophysical Research: Solid Earth, 1991, 96(B12): 20 353-20 364 DOI:10.1029/91JB00421
(  0) 0) |
2. China Earthquake Networks Center, 5 Nanheng Street, Sanlihe, Beijing 100045, China
 2023, Vol. 43
2023, Vol. 43


