传统大坝变形预测方法一般利用单一的预测模型,它们方便简单、各具特点,但往往难以得到很好的预测结果,在实际应用中有一定的局限性。为了提高大坝变形预测精度,将传统的预测方法与智能优化算法结合进行预测成为新的趋势[1]。黄军胜等[2]建立以经验模态分解法(empirical mode decomposition,EMD)和果蝇优化算法(fruit fly optimization algorithm,FOA)优化BP神经网络的大坝变形预测模型,解决了模型陷入极值的问题,提高了模型收敛速度,但忽略了EMD中的模态混叠问题,导致分解得到的分量不精确。陈竹安等[3]提出一种结合变分模态分解(variational mode decomposition,VMD)和长短期记忆(long short-term memory,LSTM)神经网络的大坝变形预测模型,提升了分解-预测-重构模型的预测性能,但忽略了LSTM超参数的寻优,影响最后的预测精度。张明岳等[4]建立一种结合VMD和双向长短期记忆(bidirectional long short-term memory,BiLSTM)神经网络的滑坡位移预测模型,能更深入地挖掘原始数据包含的信息,有效提高了预测精度,但模型训练收敛时间较长。
针对上述模型预测精度不高、训练时间较长等问题,本文采用VMD和猎食者算法(hunter-prey optimizer,HPO)优化的BiLSTM,建立VMD-HPO-BiLSTM组合预测模型,并将该模型应用到某水电站大坝变形预测中,以验证其可行性。
1 基本原理与方法 1.1 变分模态分解VMD常用于处理非线性信号,可以将复杂的原始数据进行分解,得到一系列模态分量[5],能有效提取大坝变形数据的特征,降低其非线性和非平稳性对预测结果的影响。
VMD算法的主要步骤为:1)将大坝变形原始信号通过希尔伯特变换,得到一系列的模态函数uk(t),计算得到单侧频谱;2)将频谱变换为基频带,通过估算带宽来构造对应的约束性变分问题;3)将约束性变分问题转化为非约束性变分问题[6]。计算方程如下:
| $ \begin{gathered} L\left(\left\{u_k\right\}, \left\{u_k\right\}, \lambda\right)= \\ \alpha \sum\limits_k\left\|\partial_t\left[\left(\delta(t)+\frac{\mathrm{j}}{{\rm{ \mathsf{ π} }} t}\right) * u_k(t)\right] \mathrm{e}^{-\mathrm{j} \omega_k t}\right\|_2^2+ \\ \left\|f(t)-\sum\limits_k u_k(t)\right\|_2^2+\left\langle\lambda(t), f(t)-\sum\limits_k u_k(t)\right\rangle \end{gathered} $ | (1) |
式中,{uk}和{ωk}分别为模态分量和对应的中心频率,α为惩罚函数,λ为拉格朗日乘子。多次实验结果表明,当α取2 000时,分解结果较好,因此本文将α设置为2 000。利用乘法算子交替方向法来寻求非约束性变分问题的鞍点,从而求解出VMD的k个模态分量。
1.2 HPOHPO通过模拟狼、豹子和狮子等食肉动物对鹿和羊等猎物的捕食过程对问题进行寻优,具有收敛性好、参数少以及寻优能力强的优点[7]。
假设HPO在d维空间中进行搜索,每个猎人或猎物的位置为xi=(x1, x2, …, xn), 那么其搜索代理在d维空间中的下一个位置的更新公式为[8]:
| $ \begin{gathered} x_i(t+1)= \\ \left\{\begin{array}{l} x_i(t)+0.5\left[\left(2 C Z P_{\mathrm{pos}}-x_i(t)\right)+\right. \\ \left.\left(2(1-C) Z \mu-x_i(t)\right)\right], R_5 <\beta \\ T_{\mathrm{pos}}+C Z \cos \left(2 {\rm{ \mathsf{ π} }} R_4\right)\left(T_{\mathrm{pos}}-x_i(t)\right), R_5 \geqslant \beta \end{array}\right. \end{gathered} $ | (2) |
式中,x(t)为搜索代理的当前位置,x(t+1)为搜索代理的下一次迭代位置,R5为[0, 1]范围内的随机数,β为一个调节参数,设为0.1。当R5 < β,搜索代理将被视为猎人,其猎物的位置为Ppos,μ为所有位置的平均值;当R5≥β,搜索代理将被视为猎物,Tpos为全局最优位置,R4为范围[-1, 1]内的随机数,C为平衡参数,Z为自适应参数。
1.3 BiLSTMBiLSTM在LSTM的基础上增加了一个反向LSTM层,结合前向和后向的输入序列信息,能够更深入地挖掘原始数据所包含的信息[9]。BiLSTM结构如图 1表示,其输出ht′为:

|
图 1 BiLSTM结构 Fig. 1 BiLSTM structure |
| $ h_t^{\prime}=w_y \cdot\left[\vec{h}_t, \overleftarrow{h}_t\right]+b_y $ | (3) |
式中,
以引起大坝发生变形位移的因素作为模型的输入变量,主要为水压、温度和时效因子。用T0表示温度因子,其正余弦谐波因子取sin(2πt/365)、sin(4πt/365)、cos(2πt/365)、cos(4πt/365),用H1、H12、H13表示水压因子,用θ、lnθ表示时效因子,其中θ=0.01t(t为当前观测距离起始观测的天数)[10]。选取H1、T0、sin(2πt/365)、sin(4πt/365)、θ、lnθ等6个影响因子作为模型输入变量。
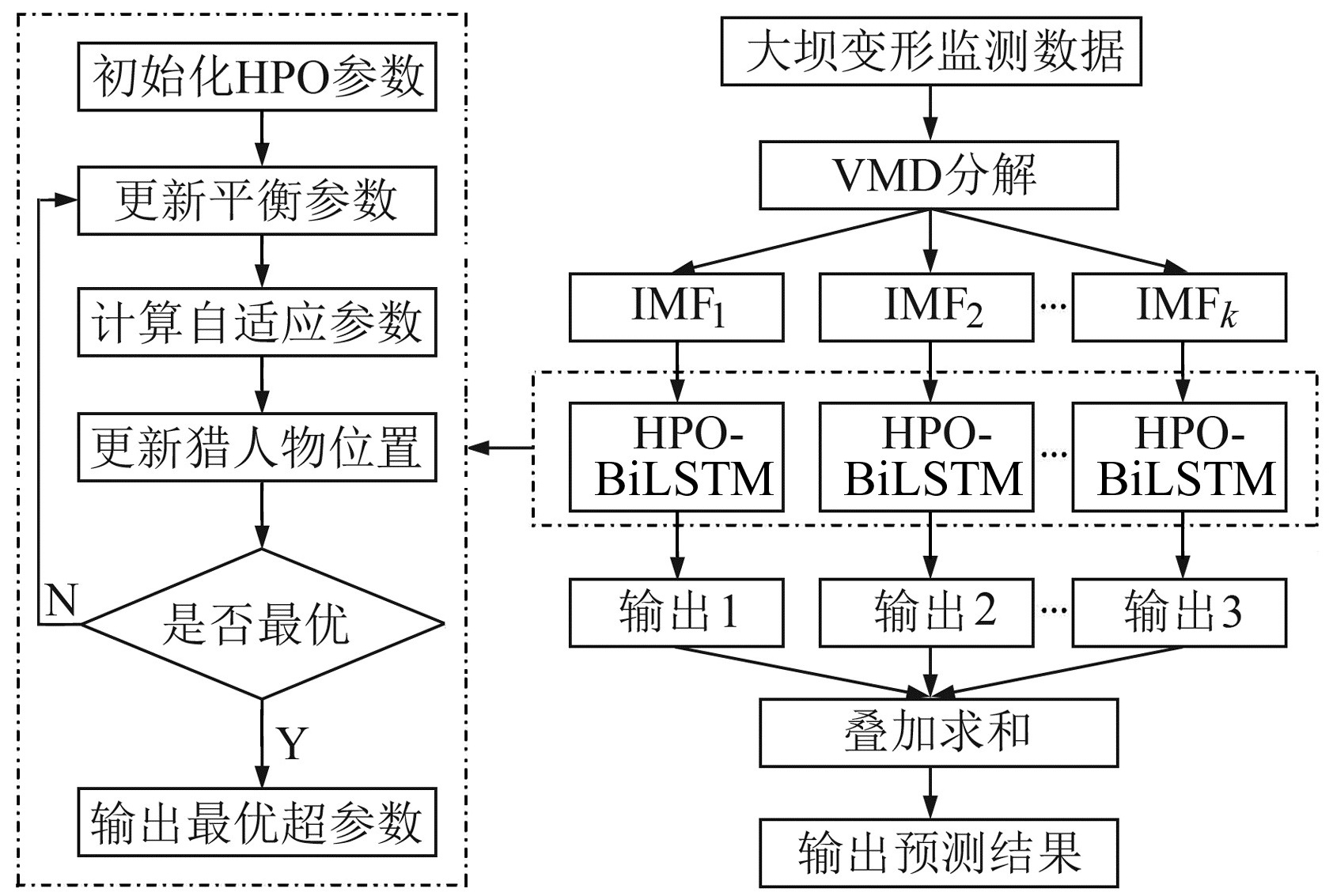
2.2 模型构建将VMD与BiLSTM结合,并利用HPO对BiLSTM模型进行优化,从而得到基于VMD-HPO-BiLSTM的大坝变形预测模型。使用VMD分解大坝原始数据,得到K个分量,将训练集分量以及对应的影响因子变量输入到BiLSTM模型中进行训练。此时需要确定BiLSTM模型的2个隐藏层节点数、学习率和训练次数,而使用试凑法的时间成本太高。为此,利用HPO算法进行优化,得到最优参数值。VMD-HPO-BiLSTM模型的流程如图 2所示。
|
图 2 VMD-HPO-BiLSTM模型流程 Fig. 2 Flow chart of VMD-HPO-BiLSTM model |
VMD-HPO-BiLSTM模型构建的具体步骤如下:
1) 利用VMD对大坝变形数据进行分解, 得到各个模态分量,并进行归一化处理,同时划分前70%为训练集,后30%为测试集;
2) 根据各个分量特征分析其影响因素;
3) 选择待优化参数,将BiLSTM模型中2个隐藏层节点数、学习率和训练次数作为寻优对象;
4) 初始化HPO算法的参数,包括种群大小、最大迭代次数、平衡参数、自适应参数以及待优化参数的取值范围;
5) 输入预处理后的训练集数据及对应影响因素,利用HPO算法进行寻优,不断更新平衡参数,对猎人和猎物位置进行更新,直到符合最优解要求结束,输出最优参数到BiLSTM;
6) 根据最优的2个隐藏层节点数、学习率和训练次数建立VMD-HPO-BiLSTM模型;
7) 利用VMD-HPO-BiLSTM模型对各分量测试集进行预测,将各分量预测结果相加,同时反归一化处理得到最终预测结果。
采用均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)作为模型预测结果的精度评价指标。
3 工程应用 3.1 工程简介选取吉林省某水电站大坝1985-01-04~1990-02-20共250期的变形监测数据,包括坝体温度数据、上游库水位数据以及某坝段监测点水平位移监测数据,如图 3所示。将前175期大坝变形数据划分为训练集,后75期数据划分为测试集。由图 3可见,监测点的水平位移变形数据具有明显的非线性和非平稳性特征,本文以此为基础进行基于VMD-HPO-BiLSTM模型的大坝变形预测研究。

|
图 3 大坝原始监测数据 Fig. 3 Dam raw monitoring data |
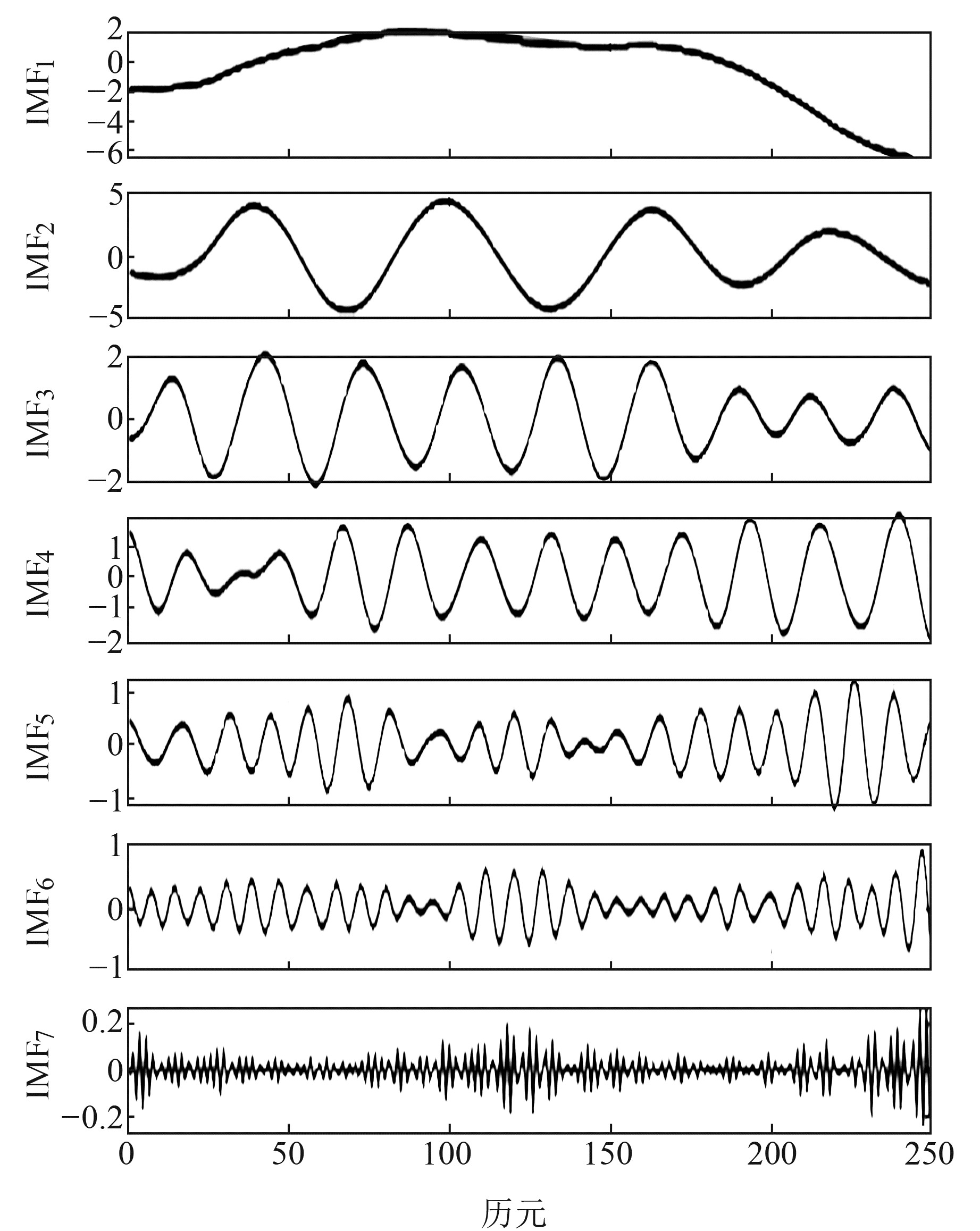
首先,对监测点的数据进行VMD,经多次实验,k取7时分解效果较好,因此设k=7,将数据分解为7组不同频率尺度的IMF分量,如图 4所示。从图 4看出,各分量依次从低频到高频分布,低频分量IMF1、IMF2主要是趋势分量,呈现大坝的长期变形趋势,其与水位和温度变化无明显相关性,故只考虑时效;较低频率分量IMF3~IMF6为波动分量,反映大坝变形数据的周期性趋势,其变化趋势与温度变化趋势相近,故考虑其影响因素为温度;高频分量IMF7可认为是大坝变形数据的随机影响部分,振幅较大,考虑其影响因素为水位、温度及时效。
|
图 4 VMD分量 Fig. 4 VMD components |
其次,将通过VMD得到的训练集分量分别构建HPO-BiLSTM模型,并输入对应影响因素。利用HPO算法对BiLSTM的2个隐藏层节点数、学习率和训练次数进行优化。经多次实验,将上述参数取值范围分别设为[1, 100]、[0.001, 0.01]和[1, 200]。同时将HPO算法进行初始化,其种群大小设为5,最大迭代次数设为20。通过HPO算法训练得到子序列BiLSTM的超参数如表 1所示。
|
|
表 1 子序列分量预测参数 Tab. 1 Prediction parameters of sub-series components |
最后,将所得测试集数据及影响因素输入到优化参数后的模型中,预测对应的变形位移量,将各个分量预测值相加得到最后的预测结果。
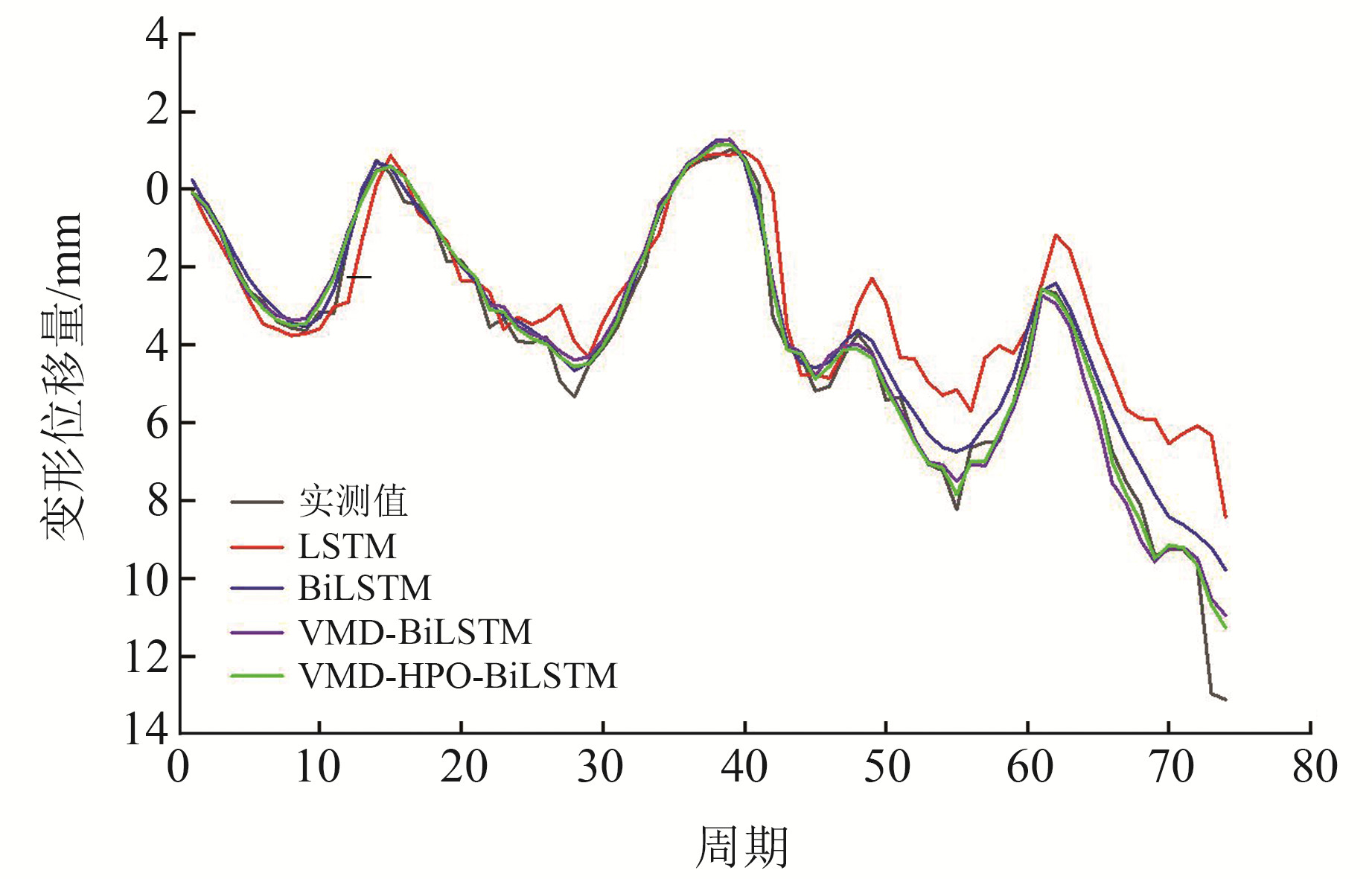
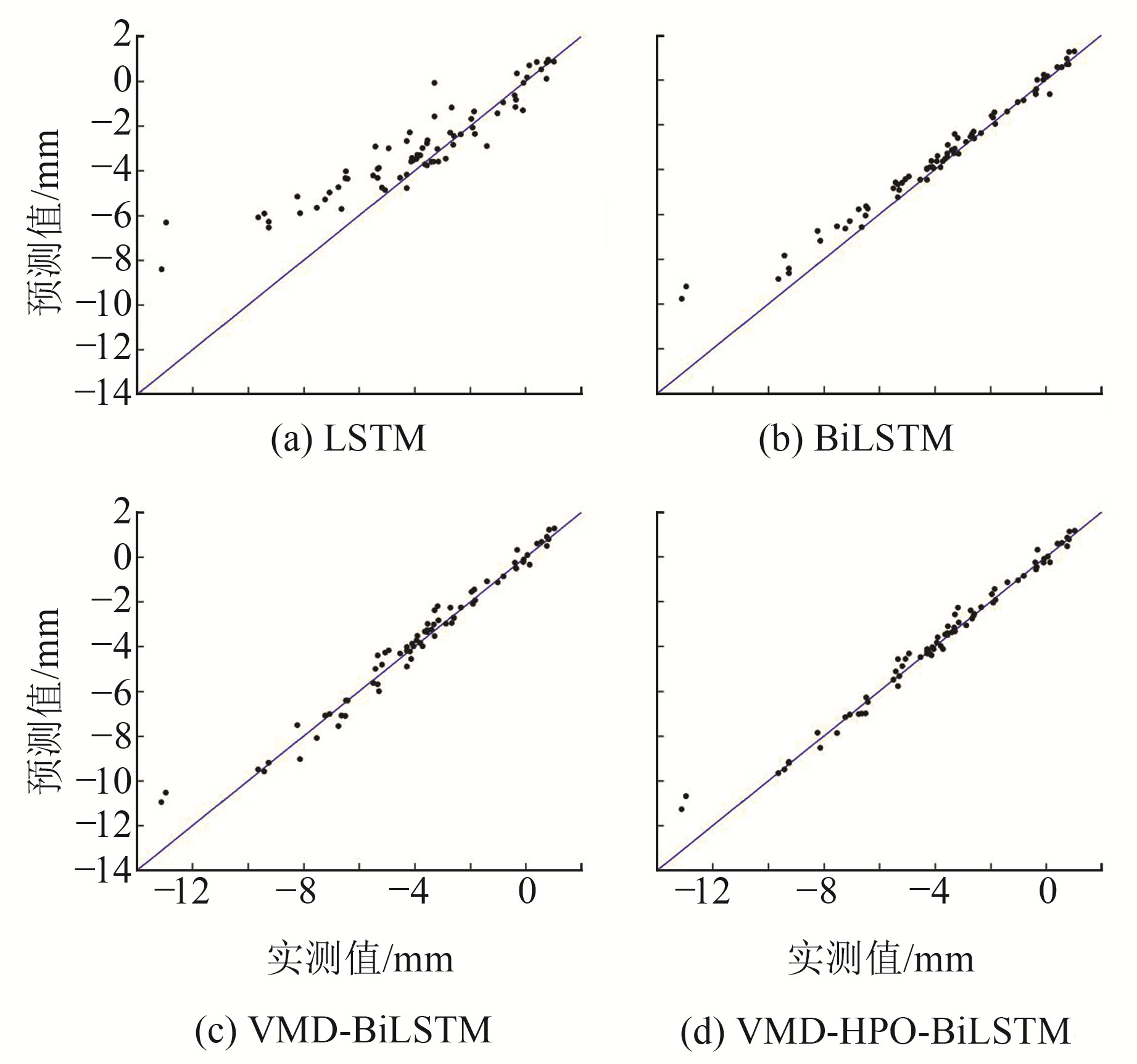
3.3 模型预测及分析为验证VMD-HPO-BiLSTM模型的性能,将其与LSTM、BiLSTM和VMD-BiLSTM模型进行对比。统一采用原始数据作为输入,设置40个隐含层节点数以及相同的模型训练次数,采用RMSE、MAE、MAPE作为模型预测效果的评价指标,各模型测试结果如图 5所示,预测值与实测值的对比如图 6所示,各模型的评估指标如表 2所示。
|
图 5 各模型预测结果 Fig. 5 Prediction results of each model |
|
图 6 实测值与预测值对比 Fig. 6 Comparison of measured values and predicted values |
|
|
表 2 各模型预测性能对比 Tab. 2 Comparison of prediction performance of each model |
从图 5看出,单一预测模型中,BiLSTM模型预测结果优于LSTM模型,LSTM模型的预测偏差较大,具有滞后性,测试集所得到的预测值与实测值具有明显的差异,而BiLSTM模型预测较贴近于实际值,但在中后段预测曲线出现明显偏离,呈现出不稳定性。相比于单一模型,组合模型VMD-BiLSTM对测试集的预测效果更好,但与BiLSTM模型相似,其在中后段数据预测效果较差,明显偏离真实值,这是因为BiLSTM网络超参数没有得到最优解。相比于以上模型,基于VMD-HPO-BiLSTM模型的预测效果最好,虽然某些突变数据上的预测值与实际值有所差异,但总体预测结果与实际值一致,波动周期也近似,能够真实反映出监测点位移的变形情况。
从图 6可知,预测结果最好的模型是VMD-HPO-BiLSTM,其余依次是VMD-BiLSTM、BiLSTM、LSTM。
从表 2可以看出,相比于LSTM模型,BiLSTM模型的3项评价指标明显降低,尤其是MAPE降低28%左右,这是因为BiLSTM模型能够同时保存过去和未来的信息,更好地提取各数据间的特征,得到较好的预测结果。对比单一模型与VMD-BiLSTM模型可以发现,经过VMD的BiLSTM模型预测效果更优,3项评价指标都有所下降,体现了组合预测模型使预测过程更细致化、精确化的特点,说明VMD可降低大坝变形数据的非线性和非平稳性对预测精度的影响。对比VMD-BiLSTM模型与VMD-HPO-BiLSTM模型可以看出,后者精度更高,预测效果更好,其RMSE、MAE、MAPE分别为0.446 mm、0.264 mm、18.593%,均远低于其他模型,说明VMD-HPO-BiLSTM模型具有更高的预测精度,可应用于大坝变形预测。
4 结语本文将VMD和BiLSTM引入大坝变形预测研究,并结合HPO优化算法,建立基于VMD-HPO-BiLSTM的大坝变形预测模型,通过工程实例进行对比研究,得到以下结论:
1) 将VMD应用于大坝变形数据,可以降低大坝变形数据非线性和非平稳性对预测精度的影响,有效降低原始数据的复杂性。同时,采用HPO优化BiLSTM的超参数,能够有效提高BiLSTM模型的泛化能力以及预测精度。
2) 工程实例表明,VMD-HPO-BiLSTM模型的预测精度明显优于LSTM、BiLSTM和VMD-BiLSTM模型,验证了该模型应用于大坝变形预测的准确性和可行性。
尽管VMD-HPO-BiLSTM模型预测结果较好,但其仅考虑了BiLSTM模型的超参数寻优,而忽略了VMD中参数k和α的优化,对此仍需要进行进一步研究。
| [1] |
胡祚晨. 基于STL-CS-LSTM组合模型的大坝变形预测方法研究[D]. 赣州: 江西理工大学, 2021 (Hu Zuochen. Research on Dam Deformation Prediction Method Based on STL-CS-LSTM Combination Model[D]. Ganzhou: Jiangxi University of Science and Technology, 2021)
(  0) 0) |
| [2] |
黄军胜, 黄良珂, 刘立龙, 等. 基于EMD-FOA-BP神经网络的大坝变形预测研究[J]. 水力发电, 2019, 45(2): 106-110 (Huang Junsheng, Huang Liangke, Liu Lilong, et al. Study on Dam Deformation Prediction Based on EMD-FOA-BP Neural Network[J]. Water Power, 2019, 45(2): 106-110)
(  0) 0) |
| [3] |
陈竹安, 熊鑫, 游宇垠. 变分模态分解与长短时神经网络的大坝变形预测[J]. 测绘科学, 2021, 46(9): 34-42 (Chen Zhu'an, Xiong Xin, You Yuyin. Variational Mode Decomposition and Long Short Time Neural Network for Dam Deformation Prediction[J]. Science of Surveying and Mapping, 2021, 46(9): 34-42)
(  0) 0) |
| [4] |
张明岳, 李丽敏, 温宗周. 基于变分模态分解和双向长短时记忆神经网络模型的滑坡位移预测[J]. 山地学报, 2021, 39(6): 855-866 (Zhang Mingyue, Li Limin, Wen Zongzhou. An Updated Approach to Predict Landslide Displacement by Combining Variational Modal Decomposition with Bidirectional Long Short-Term Memory Neural Network Model[J]. Mountain Research, 2021, 39(6): 855-866)
(  0) 0) |
| [5] |
Dragomiretskiy K, Zosso D. Variational Mode Decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544 DOI:10.1109/TSP.2013.2288675
(  0) 0) |
| [6] |
韩斐, 牛瑞卿, 李士垚, 等. 基于变分模态分解和深度置信神经网络模型的滑坡位移预测[J]. 长江科学院院报, 2020, 37(8): 61-68 (Han Fei, Niu Ruiqing, Li Shiyao, et al. Landslide Displacement Prediction Based on Variational Mode Decomposition and Deep Confidence Neural Network Model[J]. Journal of Yangtze River Scientific Research Institute, 2020, 37(8): 61-68)
(  0) 0) |
| [7] |
Naruei I, Keynia F, Molahosseini A S. Hunter-Prey Optimization: Algorithm and Applications[J]. Soft Computing, 2022, 26: 1 279-1 314 DOI:10.1007/s00500-021-06401-0
(  0) 0) |
| [8] |
Ramadan H A, Khan B, Zaki Diab A A. Accurate Parameters Estimation of Three Diode Model of Photovoltaic Modules Using Hunter-Prey and Wild Horse Optimizers[J]. IEEE Access, 2022, 10: 87 435-87 453 DOI:10.1109/ACCESS.2022.3199001
(  0) 0) |
| [9] |
王欢, 李鹏, 曹敏, 等. 基于CNN_BiLSTM的长短期电力负荷预测方法[J]. 计算机仿真, 2022, 39(3): 96-103 (Wang Huan, Li Peng, Cao Min, et al. Long-Term and Short-Term Power Load Online Prediction Method Based on CNN_BiLSTM[J]. Computer Simulation, 2022, 39(3): 96-103)
(  0) 0) |
| [10] |
杨恒, 岳建平, 邢尹, 等. 基于深度全连接神经网络的大坝变形预测研究[J]. 大地测量与地球动力学, 2021, 41(2): 162-166 (Yang Heng, Yue Jianping, Xing Yin, et al. Research on Dam Deformation Prediction Based on Deep Fully Connected Neural Network[J]. Journal of Geodesy and Geodynamics, 2021, 41(2): 162-166)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


