变形监测数据一般包含真值和噪声2个部分,对变形监测数据进行去噪处理、提取变形特征、分析变形规律,是变形分析研究的重要内容[1]。小波分析具有良好的时频特性,被广泛应用于变形分析中,特别是小波阈值去噪在非平稳变形监测数据处理中取得了较好的效果[2-3]。众多学者从影响小波去噪的关键因素出发,如小波分解层数[4-5]、去噪评价[6-7]、阈值函数[8-10]、阈值估计[8-11]等对传统小波阈值去噪进行研究。在阈值估计方面,常用的4种阈值分别为通用阈值、启发式阈值、自适应阈值和极大极小阈值。其中,自适应阈值和极大极小阈值选取规则比较保守,仅将部分系数置0;而通用阈值和启发式阈值选取规则的去除噪声效果更佳,但易将有用信号的高频部分当作噪声信号除去[9]。考虑到噪声在小波变换下随尺度增大而减小的特性,学者们给出了改进阈值估计算法,取得了一定效果,但也存在一些不足。如李明峰等[8]给出的阈值算法首层阈值估计过小,去噪不彻底;甘若等[10]、赵瑞珍等[11]给出的阈值算法首层阈值估计过大,易产生“过扼杀”小波系数的现象,且上述文献都没有考虑带噪小波系数含噪幅度随尺度增加而减小的函数关系。基于以上问题,本文提出一种新的小波阈值估计算法,并通过理论分析、工程实例验证其优越性和有效性。
1 小波阈值去噪法小波阈值去噪是基于小波变换的“集中”或“聚焦”能力。通常认为,信号在经过小波变换后,由信号产生的小波系数包含有信号的重要信息,其幅值大、数目少,而噪声对应的小波系数幅值小、数目多。通过在不同分解尺度上选取合适的阈值,并将小于该阈值的小波系数置0,保留大于阈值的小波系数,使信号噪声得到有效抑制,最后经过小波逆变换,得到去噪后的重构信号。
1.1 ZR阈值法考虑到噪声在小波变换下随尺度增大而减小的特性[10],给出小波阈值法的改进法(称为ZR阈值法)[11]:
| $ \hat{d}_{j, k}=\left\{\begin{array}{l} \operatorname{sgn}\left(d_{j, k}\right) \sqrt{d_{j, k}^2-\lambda_j^2}, \left|d_{j, k}\right| \geqslant \lambda_j \\ 0, \left|d_{j, k}\right| <\lambda_j \end{array}\right. $ | (1) |
式中,
当尺度j=1时,
对于均值为0、方差为σ2的高斯白噪声n(t),其二进小波变换为WTj, kn(t),若小波函数ψj, k(t)为实函数时,则有[4]:
| $ \left|\mathrm{WT}_{j, k} n(t)\right|^2=\left|\iint_R n(t) \psi_{j, k}(t) \mathrm{d} t\right|^2 $ | (2) |
由于E[n(t)n(t)]=σ2,小波函数ψj, k(t)为小波基ψ(t)伸缩平移所得,小波函数中每一个都有规范化的范数‖ψj, k(t)‖=‖ψ‖=1,故:
| $ E\left[\left|\mathrm{WT}_{j, k} n(t)\right|^2\right]=\frac{\sigma^2}{2^j} $ | (3) |
即随着小波分解尺度的增加,含有噪声的观测序列在低频信号中噪声影响幅度按1/2的规律逐渐减小[12]。随着分解尺度的增加,高一级尺度上的低频信号中含有的噪声影响幅度会越来越小,曲线也会也来越光滑。
对变形观测数据序列进行如式(4)所示的小波分解与重构:
| $ \begin{gathered} a_{n+1}=a_n+d_n=a_{n-1}+d_{n-1}+d_n= \\ \cdots=a_0+d_1+d_2+\cdots+d_n \end{gathered} $ | (4) |
式中,an为低频信号,表现为趋势项,dn为高频信号,含有噪声、粗差等局部变形信息。
设an噪声影响幅度为σ2,由以上分析规律可知,an-1噪声影响幅度为σ2/2,由式(4)可知,dn-1=an-an-1,即an噪声影响幅度σ2在高一级尺度上一分为二,也就是an-1分解到的噪声影响幅度为σ2/2,dn-1分解到的噪声影响幅度为σ2/2。同理,dn-2=an-1-an-2,dn-2分解到的噪声影响幅度为σ2/4。因此,随着分解尺度的增加,高频信号分解到的噪声影响幅度也是按1/2的规律逐渐减小。
综上所述,噪声在小波变换下随着分解尺度的增大而减小,且高频信号分解到的噪声影响幅度也是按1/2的规律逐渐减小。据此,本文给出新阈值计算公式(称1/2阈值法):
| $ \hat{\lambda}_j=\sigma \sqrt{2 \ln N} / 2^{j-1} $ | (5) |
式中,
多期的变形监测信号一般包括趋势项、周期项及多种噪声,为保证与实际观测数据相符合,构造复合信号进行仿真模拟实验。如图 1所示,仿真信号时长为120 s,其中包括2个趋势项、2个周期项及随机噪声项,实验采用MATLAB中自带的awgn函数,添加信噪比为db10的高斯白噪声,其表达式为:
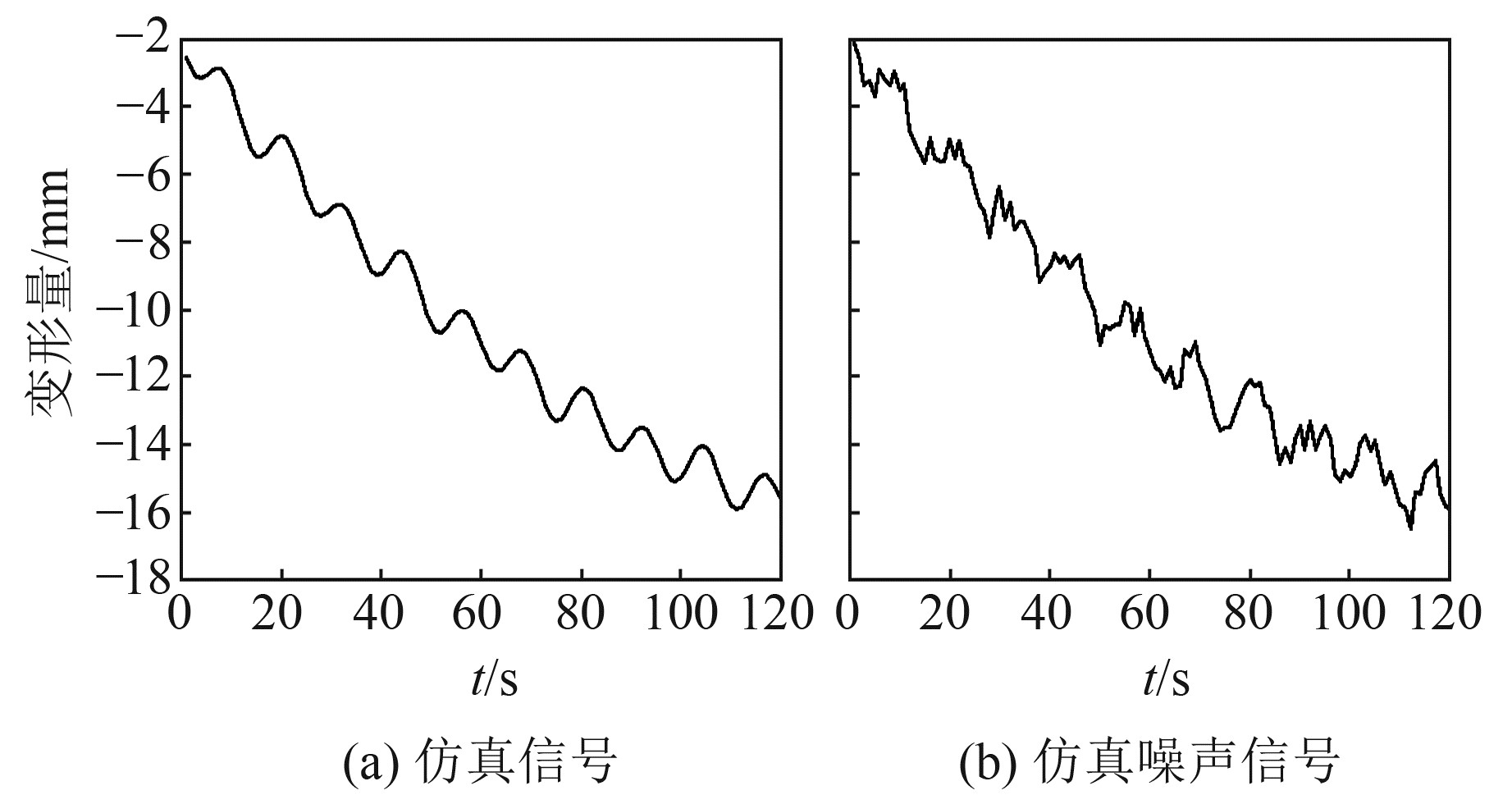
|
图 1 仿真数据 Fig. 1 Simulation data |
| $ \begin{gathered} Y=0.0006 t^2-0.1852 t- \\ 0.6499 \sin (2 {\rm{ \mathsf{ π} }} t / 12+0.1537)+ \\ 0.1477 \sin (2 {\rm{ \mathsf{ π} }} t / 20+0.4240)- \\ 2.0380+\text { noise } \end{gathered} $ |
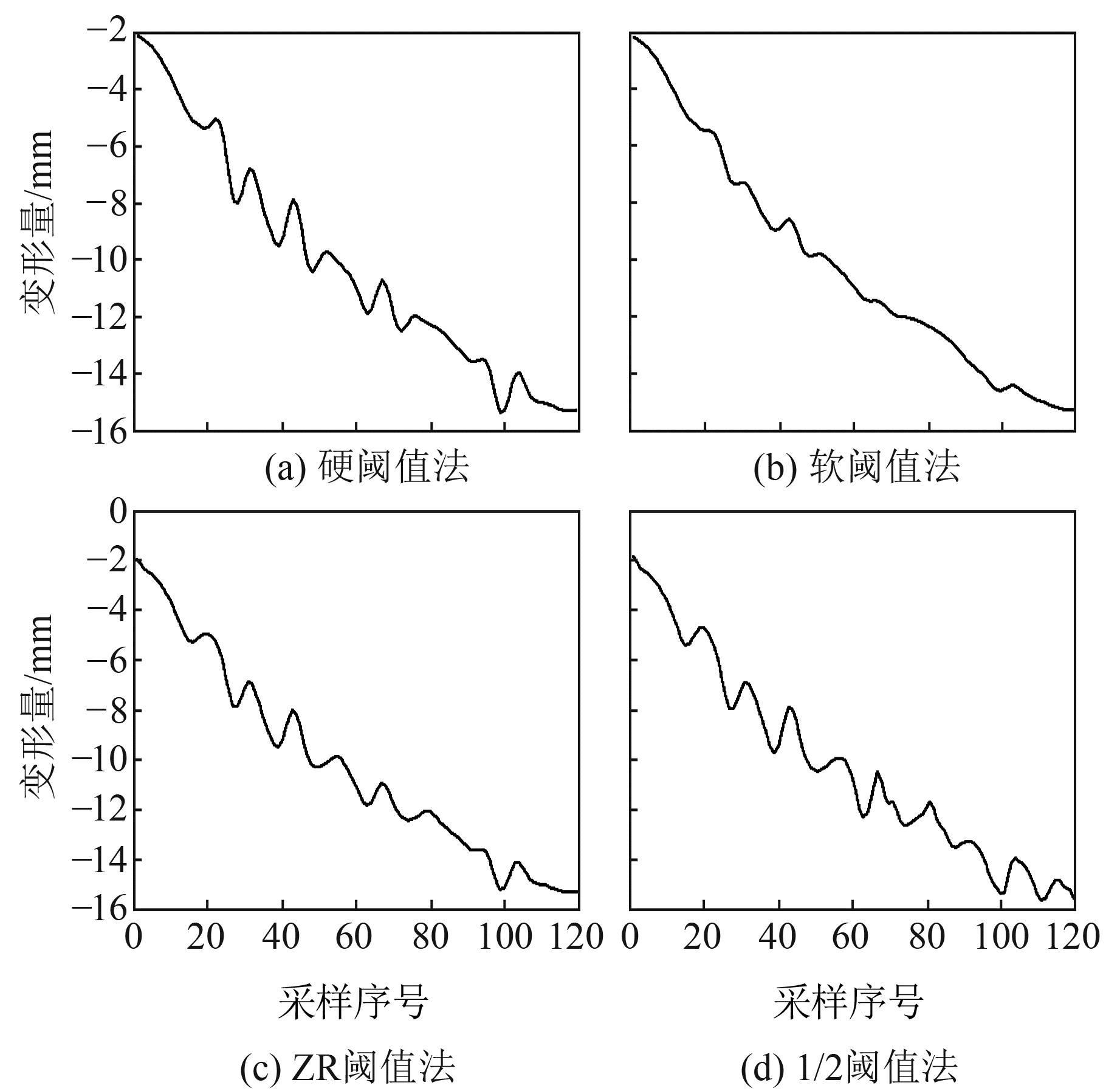
为验证本文1/2阈值法的降噪效果,采用分解能力较好的sym8小波基,使用文献[4-5]的方法确定该信号最佳分解尺度为3层。使用硬阈值方法、软阈值法、ZR阈值法进行对比,使用信噪比(SNR)、均方根误差(RMSE)作为小波去噪的评价指标。
消噪的信号如图 2所示。可以看出,软阈值法去噪后曲线过于光滑,未能有效提取周期性信号,去噪效果最差;硬阈值法由于阈值函数的不连续性,在采样序号75处有较大折线现象,即伪吉布斯现象,对周期性信号的提取有所提高,但在采样序号5~10处未能提取到信息;ZR阈值法去噪信号曲线光滑,无多余折线现象,在采样序号5~10处也未能提取到信息;1/2阈值法去噪信号曲线光滑程度最好,无多余振荡,对周期性信号提取最好。从表 1可知,1/2阈值法去噪的SNR最大,RMSE最小,去噪效果最佳,说明1/2阈值法去噪是可行的。

|
图 2 4种方法去噪结果 Fig. 2 Denoising results of four methods |
|
|
表 1 4种阈值法的去噪指标 Tab. 1 Denoising indicators of four threshold methods |
为进一步验证本文小波阈值法去噪的有效性和优越性,对文献[10]中某江岸危岩上H监测点10 a的沉降监测数据进行实例分析,如图 3所示。可以看出,该危岩H点的高程随时间的增加呈现出下降趋势,同时含有周期性变形信息。由于各种不确定的因素,该信号含有很多毛刺,严重影响变形监测的准确分析和后续预测,因此需要对其进行去噪处理。

|
图 3 原始变形监测数据 Fig. 3 Original measuring deformation data |
为了验证1/2阈值法去噪的优越性,采用分解能力较好的sym8小波基,使用文献[4-5]的方法确定该信号最佳分解尺度为3层,同时使用硬阈值法、软阈值法、ZR阈值法进行对比,去噪结果如图 4所示。可以看出,软阈值法由于估计小波系数和带噪小波系数间有恒定的偏差,导致重构的信号失真比较严重,去噪后曲线过于光滑,未能有效保留周期性细节变形信息,去噪效果最差。硬阈值法由于阈值函数的不连续性,在采样序号43处有较大折线现象,即伪吉布斯现象,去噪后曲线光滑性最差,对周期性细节变形信息保留有提高,如在采样序号20~40处保留了周期性细节变形信息。ZR阈值法克服了软、硬阈值法的缺点,也考虑到噪声在小波变换下随尺度增大而减小的特性,去噪后曲线的光滑性好,对周期性细节变形信息的保留程度有所提高,如在采样序号50~60处保留了周期性细节变形信息。1/2阈值法克服了软、硬阈值法的缺点,不仅与噪声在小波变换各尺度上的传播特性相一致,也更符合带噪小波系数随分解尺度增加而减小的函数关系,去噪后曲线的光滑性好,没有多余振荡,特别是在采样序号110~120处,对周期性细节变形信息保留最好。从表 2可知,1/2阈值法去噪的SNR最大,RMSE最小,与其他阈值法去噪对比,效果更好,对周期性细节变形信息提取更准确。
|
图 4 4种方法去噪结果 Fig. 4 Denoising results of four methods |
|
|
表 2 4种阈值法的去噪指标 Tab. 2 Denoising indicators of four threshold methods |
通过理论分析与工程实例可知,本文1/2阈值法去噪效果优于软、硬阈值法及ZR阈值法,能更有效地恢复被噪声湮没的周期性细节变形信息,进一步提高去噪的精度与可靠性,更好地反映危岩变形规律。1/2小波阈值法不仅与噪声在小波变换各尺度上的传播特性相一致,也更符合带噪小波系数随分解尺度的增加而减小的函数关系。需要指出的是,变形监测数据具有受噪声干扰相对较小的特点,对噪声干扰较大的复杂信号,本文方法的去噪效果有待进一步研究。
| [1] |
杨兵, 杨志强, 田镇, 等. 联合EMD-HD和小波分解的GNSS坐标时间序列降噪分析[J]. 测绘学报, 2022, 51(9): 1 881-1 889 (Yang Bing, Yang Zhiqiang, Tian Zhen, et al. Denoising Analysis of GNSS Coordinate Time Series by Combining EMD-HD and Wavelet Decomposition[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(9): 1 881-1 889)
(  0) 0) |
| [2] |
罗甘, 梁月吉, 黄仪邦. 基于双树复小波的变形监测数据去噪分析[J]. 大地测量与地球动力学, 2018, 38(9): 958-963 (Luo Gan, Liang Yueji, Huang Yibang. Deformation Analysis Based on a Dual-Tree Complex Wavelet Transform Method[J]. Journal of Geodesy and Geodynamics, 2018, 38(9): 958-963)
(  0) 0) |
| [3] |
王民顿, 尚俊娜. 基于CEEMD和改进小波阈值法的钢架结构沉降数据去噪方法[J]. 大地测量与地球动力学, 2022, 42(11): 1 191-1 195 (Wang Mindun, Shang Junna. Denoising Method of Steel Frame Structure Settlement Data Based on CEEMD and Improved Wavelet Threshold Method[J]. Journal of Geodesy and Geodynamics, 2022, 42(11): 1 191-1 195)
(  0) 0) |
| [4] |
向东, 贡建兵. 变形序列小波消噪最佳分解尺度量化指标的确定[J]. 武汉大学学报: 信息科学版, 2014, 39(4): 467-470 (Xiang Dong, Gong Jianbing. To Determine the Quantitative Index for the Optimal Decomposition Scale in Wavelet De-Noising of Deformation Series[J]. Geomatics and Information Science of Wuhan University, 2014, 39(4): 467-470)
(  0) 0) |
| [5] |
陶珂, 朱建军. 多指标融合的小波去噪最佳分解尺度选择方法[J]. 测绘学报, 2012, 41(5): 749-755 (Tao Ke, Zhu Jianjun. A Hybrid Indicator for Determining the Best Decomposition Scale of Wavelet Denoising[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 749-755)
(  0) 0) |
| [6] |
谢政宇, 刘学广, 张巩, 等. 利用小波去噪进行步态加速度信号预处理[J]. 武汉大学学报: 信息科学版, 2022, 47(11): 1 956-1 962 (Xie Zhengyu, Liu Xueguang, Zhang Gong, et al. Gait Acceleration Signal Preprocessing with Wavelet Denoising[J]. Geomatics and Information Science of Wuhan University, 2022, 47(11): 1 956-1 962)
(  0) 0) |
| [7] |
王旭, 王昶. 一种基于熵权法的小波去噪复合评价指标[J]. 大地测量与地球动力学, 2018, 38(7): 689-694 (Wang Xu, Wang Chang. A Kind of Wavelet De-Noising Composite Evaluation Index Based on Entropy Method[J]. Journal of Geodesy and Geodynamics, 2018, 38(7): 689-694)
(  0) 0) |
| [8] |
李明峰, 欧江霞, 王永明, 等. 基于改进小波阈值去噪法的变形预测研究[J]. 大地测量与地球动力学, 2014, 34(3): 68-71 (Li Mingfeng, Ou Jiangxia, Wang Yongming, et al. Study on Deformation Prediction Based on Improved Wavelet Threshold De-Noising Method[J]. Journal of Geodesy and Geodynamics, 2014, 34(3): 68-71)
(  0) 0) |
| [9] |
王旭, 王昶. 一种改进小波阈值去噪方法的研究[J]. 大地测量与地球动力学, 2017, 37(10): 1 038-1 041 (Wang Xu, Wang Chang. Improved Wavelet Threshold De-Noising Method Research[J]. Journal of Geodesy and Geodynamics, 2017, 37(10): 1 038-1 041)
(  0) 0) |
| [10] |
甘若, 陈天伟, 郑旭东, 等. 改进的小波阈值函数对变形监测数据的去噪研究[J]. 大地测量与地球动力学, 2020, 40(1): 17-22 (Gan Ruo, Chen Tianwei, Zheng Xudong, et al. Research on Denoising of Deformation Monitoring Data by Improved Wavelet Threshold Function[J]. Journal of Geodesy and Geodynamics, 2020, 40(1): 17-22)
(  0) 0) |
| [11] |
赵瑞珍, 宋国乡, 王红. 小波系数阈值估计的改进模型[J]. 西北工业大学学报, 2001, 19(4): 625-628 (Zhao Ruizhen, Song Guoxiang, Wang Hong. Better Threshold Estimation of Wavelet Coefficients for Improving Denoising[J]. Journal of Northwestern Polytechnical University, 2001, 19(4): 625-628)
(  0) 0) |
| [12] |
文鸿雁. 基于小波理论的变形分析模型研究[D]. 武汉: 武汉大学, 2004 (Wen Hongyan. Research on Deformation Analysis Model Based on Wavelet Transform Theory[D]. Wuhan: Wuhan University, 2004)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43

