2. 中国地震局地震大地测量重点实验室,武汉市洪山侧路40号,430071
地震危险性分析是对工程场地未来可能遭遇的强地震动进行估计,是在工程场址周围地震活动性和地震地质环境研究的基础上估计工程场址的设计地震动参数。评定某个工程场址的地震危险性须考虑3个方面:1)确定该场址周围未来一定时间内可能发生破坏性地震的地点、强度和性质;2)通过强震观测数据和历史地震资料,了解地震波传播途径的区域特性,确定地震动衰减关系;3)详细勘察场地条件,分析局部场地条件对地震动的影响[1]。目前地震危险性分析方法大体上分为确定性方法和概率方法[2]两大类,其中概率地震危险性分析方法由章在墉等[3]率先引入国内,经高孟潭[4]和时振梁等[5]改进。改进后的方法能够反映我国地震活动的时空不均匀性,被广泛应用于地震安全性评价和地震小区划等工作中。
地震灾害普查中要求按国家级30″×30″网格、省级6″×6″网格、市级3″×3″网格、县级1″×1″网格划分经纬度计算地震危险性,计算控制点数量达到千万量级。若每个计算点耗时0.5 s,则省级计算点约1 000万个,耗时约1 300 h,因此优化相关计算方法是一个重要的研究课题。大空间网格的计算结果显示,各相邻点之间的危险性计算结果变化较为平稳,若能够通过大间隔网格控制点的危险性结果插值获得可靠的小空间间隔控制点的地震危险性结果,将大大节省计算时间。基于此,本文先计算120″、60″、30″、15″、9″和6″经纬度划分网格的地震危险性,然后插值得到较小网格的地震危险性结果,最后比较直接计算的小网格地震危险性结果和大空间网格插值得到的小网格地震危险性结果,评估由较大空间间隔插值所获结果的可靠性、适用性及使用要求,以讨论地震灾害风险普查中兼顾可靠性和效率的计算地震危险性的最优插值网格。
1 概率地震危险性分析方法概率地震危险性分析方法(PSHA)于20世纪80年代引入我国,之后逐渐形成了具有中国特色的考虑地震时空分布不均匀性的概率性地震危险性分析方法(CPSHA),GB 17741-2005《工程场地地震安全性评价》和GB 18036-2015《中国地震动参数区划图》(简称五代区划图)都采用CPSHA方法,其计算步骤如图 1所示,包含确定地震区带及其地震活动性参数、选定地震动衰减关系和进行地震危险性计算等主要步骤。
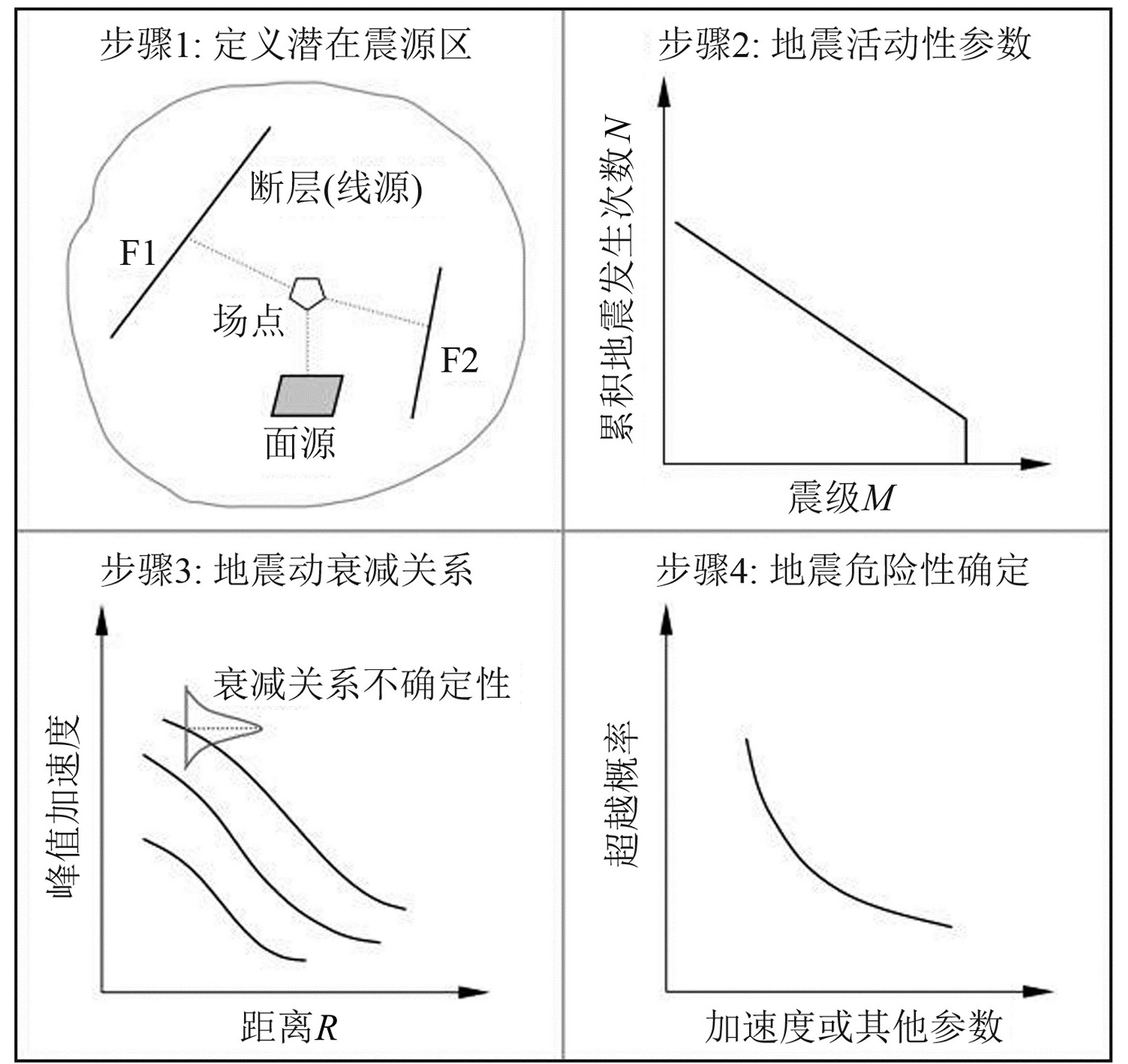
|
图 1 概率地震危险性分析步骤 Fig. 1 Steps of probabilistic seismic hazard analysis |
根据地震风险普查规范,区域的标准网格分为国家、省、市、县4种,国家级网格为30″×30″ (约1 km),省级网格为6″×6″(约200 m),市级网格为3″×3″(约100 m),县级网格为1″×1″ (约30 m)。其中30″标准网格文件可通过软件平台下载,6″标准网格严格按照标准制作,地震、地质、气象等所有灾种统一使用。标准网格基准点(西北角)为73°E、54°N,行列号向东及向南逐渐增加;标准网格制作中,行列号根据给定公式进行计算,作为对计算点的标签,使用网格点中心点坐标(xcenter,ycenter)计算地震危险性;标准网格要求经纬度保留小数点后8位,空间位置与属性信息字段的经纬度位置保持一致;分别计算50 a 63%、50 a 10%、50 a 2%和100 a 1%共4个概率水准的峰值加速度(PGA),不计算反应谱,给出基岩和场地调整的PGA,其中场地条件采用全国1 ∶100万宏观场地类别数据,场地调整系数参考《地震危险性图编制规范FXPC/DZ P-01》,场地类别根据标准网格中心点进行判别,地震危险性分级方法按照《地震危险性图编制规范FXPC/DZ P-01》以100 a 1%概率结果作为分级指标(不使用50 a 10%),分级排序采用降序(危险性最高为1级,最低为4级)。该策略的目的一方面是为了避免使用50 a 10%造成混淆误解;另一方面,万年一遇可反映计算点可能遭受的最大地震动。潜在震源区、地震活动性参数和衰减关系使用五代区划图资料,不考虑近几年的潜源调整。
因本文主要关注计算效率和插值方法的有效性问题,故区域范围统一采用计算点周围150 km范围截取潜在震源的方法确定,暂不考虑150 km范围外远大震的影响,PGA计算结果统一保留小数点后1位。
2 测试区域选取测试区范围为34.55°~35.88°N、114.80°~116.42°E(图 2),主要基于以下考虑:1)根据五代区划图,区域场地地震动分类较全,0.05~0.20 g都有,便于比较不同等级分解处插值是否合理;2)地震安全性评价报告资料丰富,便于对比;3)区域大小合适,采用不同网格间隔进行划分,网格点数跨越几千到几百万量级,利于全面研究不同量级的计算效率和精度。
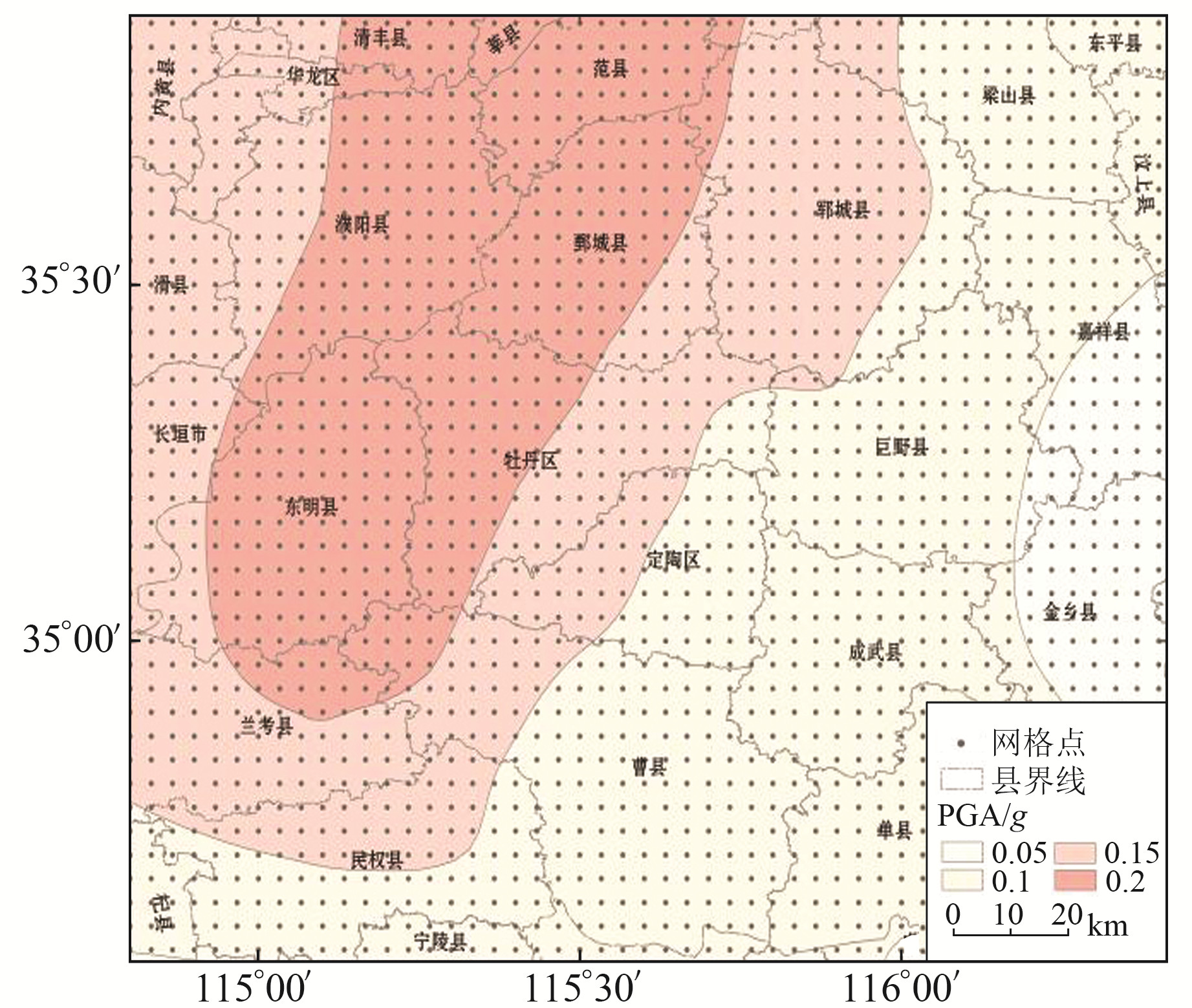
|
图 2 测试区位置及120″间隔网格点分布 Fig. 2 Location of test area and distribution of 120″ interval grid |
计算区间及网格划分参数为:全国网格划分统一起点纬度为54°,起点经度为73°,网格间隔δ为3″,分别使用120″、60″、30″、15″、9″、6″及3″进行网格划分;行号起点为10 001+int[((ycenter-54)×3 600-δ/2)/δ+0.5],列号起点为10 001+int[((xcenter-73)×3 600-δ/2)/δ+0.5],式中,int表示取整数。按照规范,不同级别的网格行列号的起点数不同,本文不作区分,只要能够通过行列号找到对应的点即可。
单个控制点地震危险性分析计算输出结果保存在以“点序号-列号-行号”命名的单独文件夹中,其中包括5个周期(0 s,0.2 s,1.0 s,2.0 s,6.0 s)的危险性结果及相应潜源的贡献、150 km范围内五代区划图中潜源分布(图 3)、各潜源的空间分布函数和风险普查要求的4个概率水准PGA。前期不同周期的危险性结果和潜源贡献分别存放在不同的文件中;后期为减少文件读写数目,尽可能提高计算效率,将危险性结果和潜源贡献结果合并存储在同一个文件中。实际计算表明,该措施对计算速度的影响不大,但可减少小文件的数目,提高计算机存储空间的利用率。风险普查要求计算4个概率水准(50 a 63%、50 a 10%、50 a 2%和100 a 1%)下5个周期的谱加速度值,由于数据量巨大,且不同周期、不同场地条件下结果类似,本文仅展示基岩场地50 a超越概率10%的PGA比较结果。

|
图 3 测试区内某个计算点周边150 km范围内五代区划图潜源分布 Fig. 3 Distribution of potential sources within 150 km of a calculation point in the test area in five generations zoning map |
将测试区划分出120″、60″、30″、15″、9″、6″和3″间隔的网格,计算所有网格点各种概率水准下的PGA。如表 1所示,不同间隔划分的总网格点数随着划分间隔的减小呈指数增长,相应的计算耗时也大幅增长。首先分别计算不同空间间隔的各网格点的地震危险性,然后根据较大空间间隔的计算结果,按照空间距离平方倒数加权的插值方式得到所有较小空间间隔点的PGA,最后将插值所得PGA与直接计算的网格点PGA(准确值)进行比较,计算误差最大值、最小值及标准差(表 2,单位Gal)。
|
|
表 1 不同空间间隔的计算量和耗时 Tab. 1 The computation amount and time of different space intervals |
|
|
表 2 不同大网格插值结果的误差最大值、最小值、标准差 Tab. 2 The maximum, minimum and standard deviation error of interpolation results with different larger grids |
表 1给出不同处理器的计算耗时,其中,CPU为i7-11700的台式机计算了全部数据,其他几种处理器只处理了15″以上间隔的数据,更小间隔的数据是根据单点速度乘以计算量估算出来的。由于每个点地震危险性计算相互独立,不存在数据交叉,可以完全并行计算而不冲突。程序采用多线程,总体来看,每个程序的线程数对速度影响并不大。单个程序运行时,CPU为i7-9850H的移动工作站计算速度最慢,计算效率约5 000点/h,CPU为i7-11700的台式机计算速度最快,计算效率约10 000点/h。为进一步提高计算速度,测试同一台计算机采用2、4、8个相同程序同时计算不同区域的方法。结果表明,计算速度总和有所提高,但无论采用多少个应用程序,单台计算机总最高计算速度约为18 000点/h,这个速度上限可能是由计算机的CPU处理能力决定的。
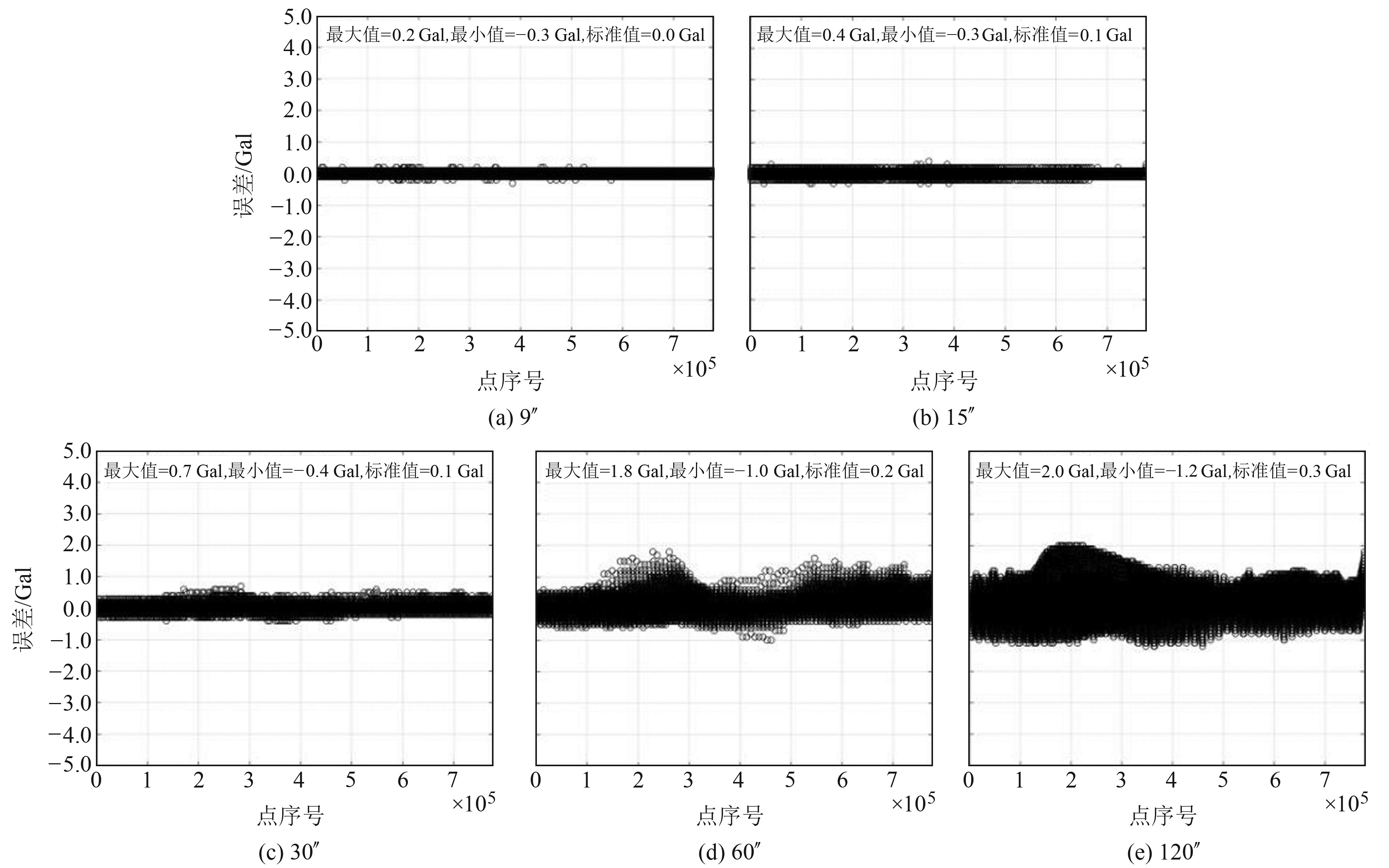
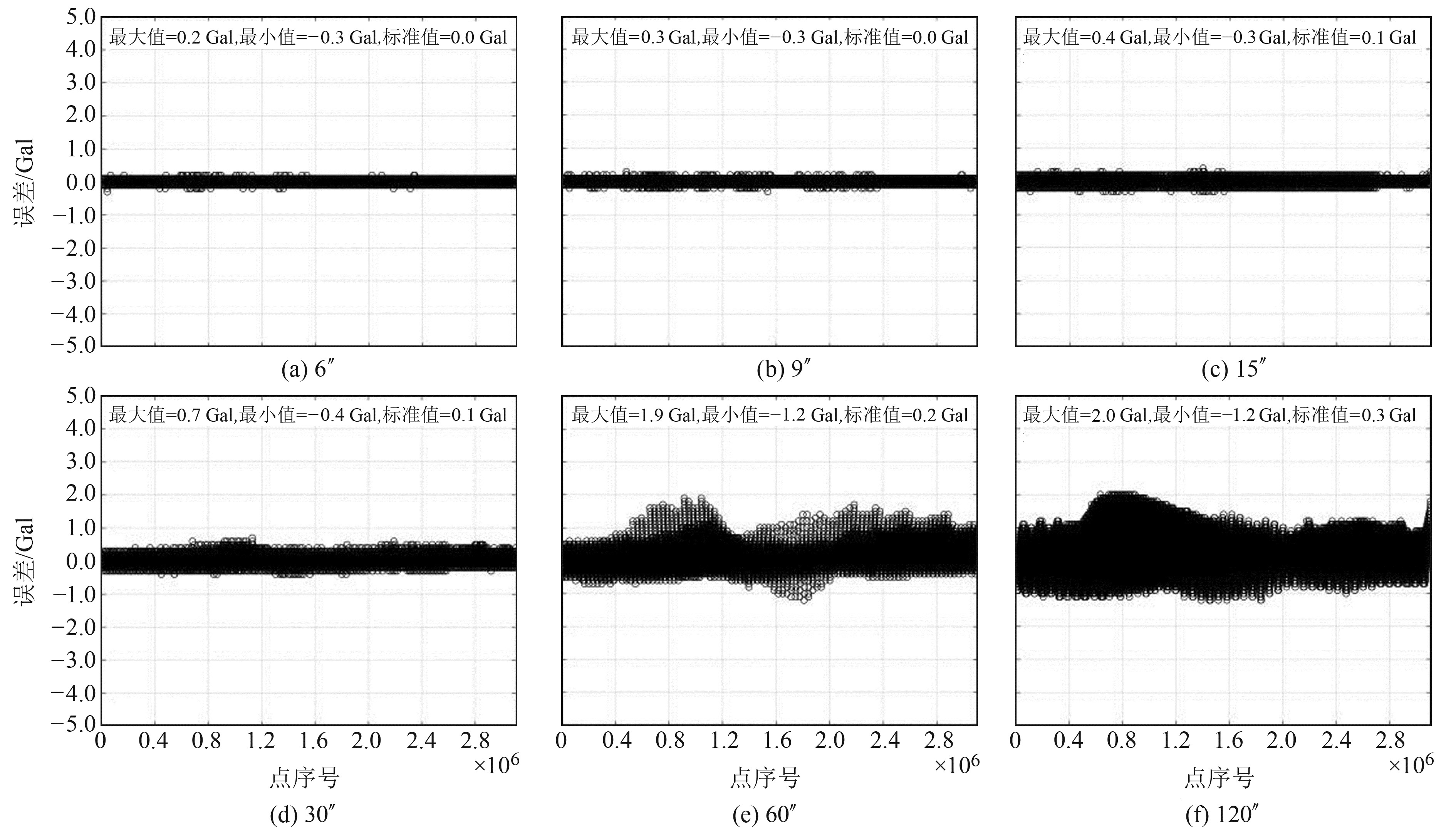
从表 2和部分大网格插值得到的小网格结果的误差分布(图 4~7)可以看出:1)利用120″网格插值结果的误差最大值都达到2.0 Gal,这可能是由大网格相邻2点危险性计算值的差值决定的;60″网格插值结果的最大误差为1.9 Gal;30″网格插值结果的最大误差为0.7 Gal;15″网格插值结果的最大误差为0.4 Gal;9″网格插值结果的最大误差为0.3 Gal;6″网格插值结果的最大误差为0.2 Gal。2)所有大网格插值结果的误差的标准差都较小,说明绝大多数点的误差较小,插值结果误差分布也说明了这一点。3)对于国家级30″网格,采用60″网格的计算值进行插值,误差小于1 Gal;对于省级6″网格,采用30″、15″和9″网格的计算值进行插值,误差小于1 Gal;对于市级3″网格,采用30″、15″、9″和6″网格的计算值进行插值,误差小于1 Gal;同理,对于县级1″网格,有理由推测采用30″、15″、9″、6″和3″网格的计算值进行插值,误差也小于1 Gal。
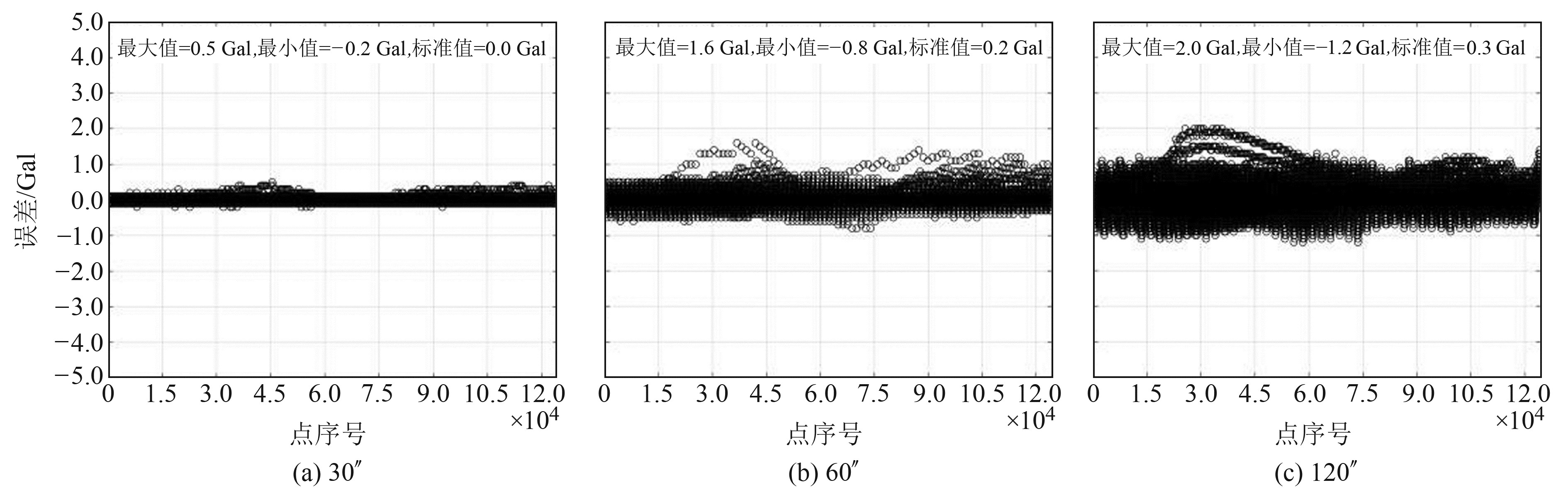
|
图 4 不同大网格插值得到15″网格PGA的误差分布 Fig. 4 The error distribution of 15″ grid PGA interpolated from different larger grids |
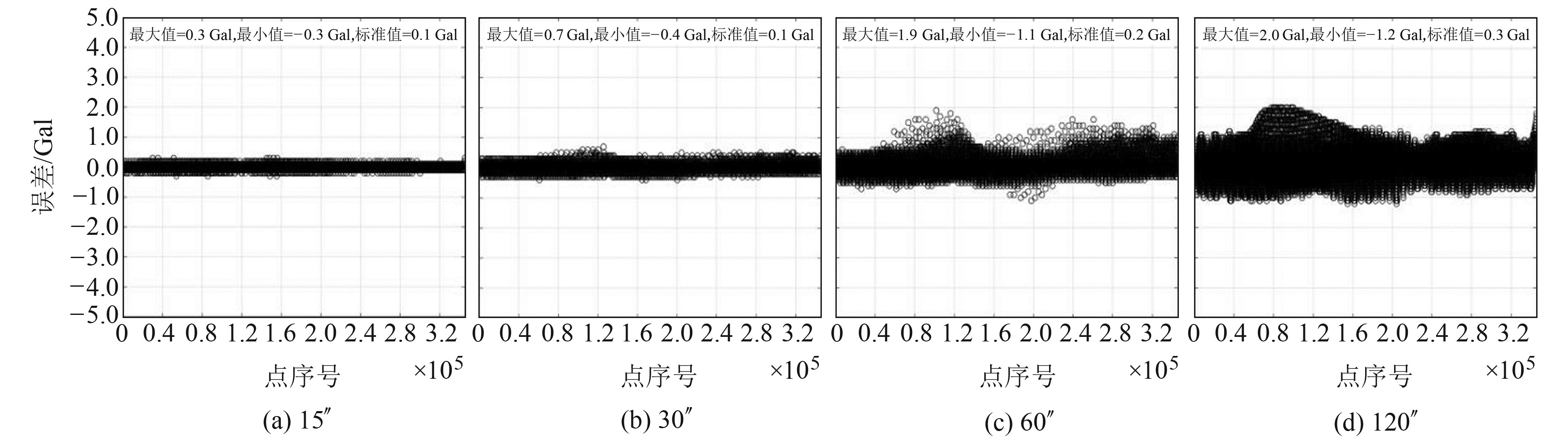
|
图 5 不同大网格插值得到9″网格PGA的误差分布 Fig. 5 The error distribution of 9″ grid PGA interpolated from different larger grids |
|
图 6 不同大网格插值得到6″网格PGA的误差分布 Fig. 6 The error distribution of 6″ grid PGA interpolated from different larger grids |
|
图 7 不同大网格插值得到3″网格PGA的误差分布 Fig. 7 The error distribution of 3″ grid PGA interpolated from different larger grids |
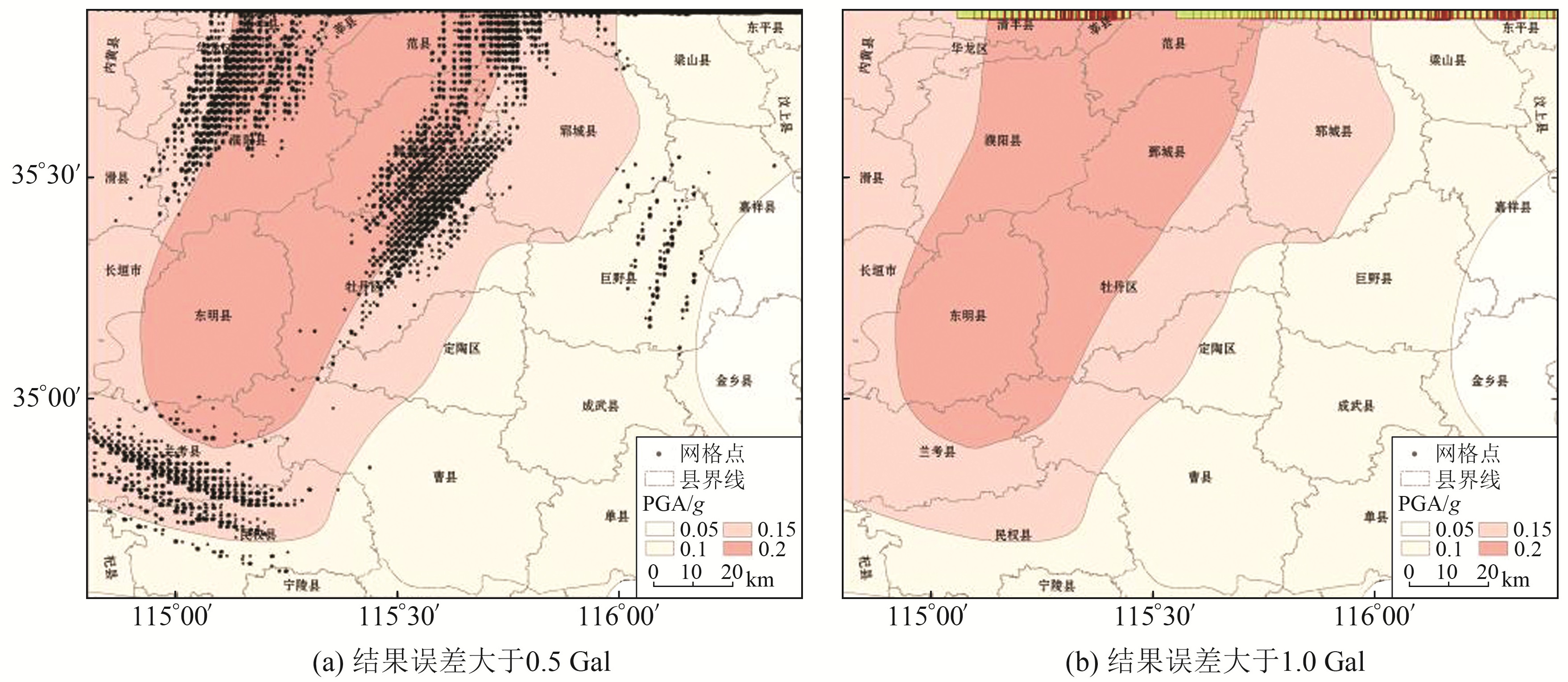
为进一步研究插值误差产生的原因,将误差较大的点投影到地图上。图 8给出由60″网格地震危险性计算值插值得到3″网格地震危险性结果时误差大于0.5 Gal和大于1.0 Gal点的分布,其他大网格计算值插值得到较小网格结果的情况与之类似。图 8(a)显示,误差较大的点主要位于分区边界处、较复杂处及计算区域边界处;图 8(b)显示,边界处误差较大,这主要是由于待插值的点位于计算值网格的外侧,而插值约束点非常少,此时采用空间距离反距加权方法不能反映变化的趋势性。可以通过扩大计算区范围,将所有需要插值的点都作为内点进行插值,或对于计算区域外边界点采用趋势外推插值的方法进行插值。由此可见,目前地震风险普查实践中一般要求计算点取行政边界外围扩大10 km的标准格网,以减少边界效应对插值结果影响的做法是合适的。
|
图 8 由60″网格插值得到3″网格的PGA误差分布 Fig. 8 The PGA error distribution of 3″ grid interpolated from 60″ grid |
本文基于五代区划图的潜在震源区划分方案,采用全国地震灾害风险普查统一的危险性计算方法,分别获得了120″、60″、30″、15″、9″和6″经纬度网格插值得到较小网格的地震危险性结果,并将其与直接计算的小网格地震危险性结果进行比较。结果表明,30″网格计算值插值得到各种小网格的地震危险性结果误差都小于1 Gal,是兼顾精度和速度比较合理的网格间隔。
由于误差较大的点主要位于地震动区划图分区边界处、较复杂处及计算区域边界处,通过扩大计算区范围,将所有需要插值的点都作为内点进行插值,可以解决计算区域边界处误差较大的问题。当然,在不需要等待很长时间的情况下,还是选择尽可能小的网格进行计算,特别是潜在震源区比较复杂的区域。
在实际地震灾害风险普查的危险性计算中,根据精度要求和时间因素进行一些前期计算实验,综合评估精度和效率,再确定计算方案是很有必要的。值得注意的是,本文主要是研究地震灾害危险性普查中地震危险性计算的效率问题,对地震危险性计算中的地震潜在震源、地震动衰减关系分析等都进行了简化,因此本文结果不能直接应用于测试区的地震安全性评价。
| [1] |
地震工程学编委会. 中国防震减灾百科全书(地震工程学)[M]. 北京: 地震出版社, 2014 (Earthquake Engineering Editorial Board. China Encyclopedia of Earthquake Prevention and Disaster Mitigation(Earthquake Engineering)[M]. Beijing: Seismological Press, 2014)
(  0) 0) |
| [2] |
Cornell C A. Engineering Seismic Risk Analysis[J]. Bulletin of the Seismological Society of America, 1968, 58(5): 1 583-1 606 DOI:10.1785/BSSA0580051583
(  0) 0) |
| [3] |
章在墉, 陈达生. 二滩水电站坝区场地地震危险性分析[J]. 地震工程与工程振动, 1982, 2(3): 1-15 (Zhang Zaiyong, Chen Dasheng. Seismic Hazard Analysis of the Ertan Dam Site[J]. Earthquake Engineering and Engineering Vibration, 1982, 2(3): 1-15)
(  0) 0) |
| [4] |
高孟潭. 地震危险性分析方法概述[J]. 国际地震动态, 1986(11): 11-14 (Gao Mengtan. Overview of Seismic Risk Analysis Method[J]. International Earthquake Dynamics, 1986(11): 11-14)
(  0) 0) |
| [5] |
时振梁, 鄢家全, 高孟潭. 地震区划原则和方法的研究: 以华北地区为例[J]. 地震学报, 1991, 13(2): 179-189 (Shi Zhenliang, Yan Jiaquan, Gao Mengtan. Research on the Methodology and Principle of Seismic Zonation—Results of the Trials in Northern China[J]. Acta Seismologica Sinica, 1991, 13(2): 179-189)
(  0) 0) |
2. Key Laboratory of Earthquake Geodesy, CEA, 40 Hongshance Road, Wuhan 430071, China
 2023, Vol. 43
2023, Vol. 43


