多年的连续工作使gPhone弹簧相对重力仪发生老化,导致观测值和实际重力值之间存在一定误差,通常用一个无量纲的常数(格值系数)对观测值进行改正[1-3]。
gPhone重力仪格值系数的标定方法主要包括长短重力基线法、垂直重力基线法、同址重力比测法、重力潮汐参数标定法以及人工加速度法。重力基线法是指使用仪器在已知段差的重力基线两端往返观测,将实测段差与已知段差进行对比得到仪器的格值系数[4],该方法需要固定不变的重力段差,实际应用存在一定误差。同址重力比测法利用绝对重力仪(AG)或超导重力仪(SG)与gPhone重力仪进行同时、同址观测,基于最小二乘原理标定gPhone重力仪格值系数[3-6],但我国gPhone台站较多(约62个)、分布较广[4],利用AG或SG比测标定难度较大、耗时较长、成本较高[4]。目前国内也没有可用于重力仪标定的人工加速度重力平台[4]。因此,以理论潮汐模型为约束,对gPhone重力仪进行格值系数标定是目前最经济、便捷的方法。
通常使用M2潮波标定法确定gPhone重力仪格值系数,但该方法只考虑了M2潮波带来的影响,忽视了其他振幅较大的潮波的影响,如O1、P1、K1、N2、S2潮波,因此存在一定的局限性,改正结果也不符合海潮负荷改正规律[3]。
本文使用理论潮汐模型进行约束,对台站gPhone重力仪进行格值系数标定,并使用潮汐因子中误差等指标评定标定结果。最后,分析我国台站格值系数随经纬度的变化规律。
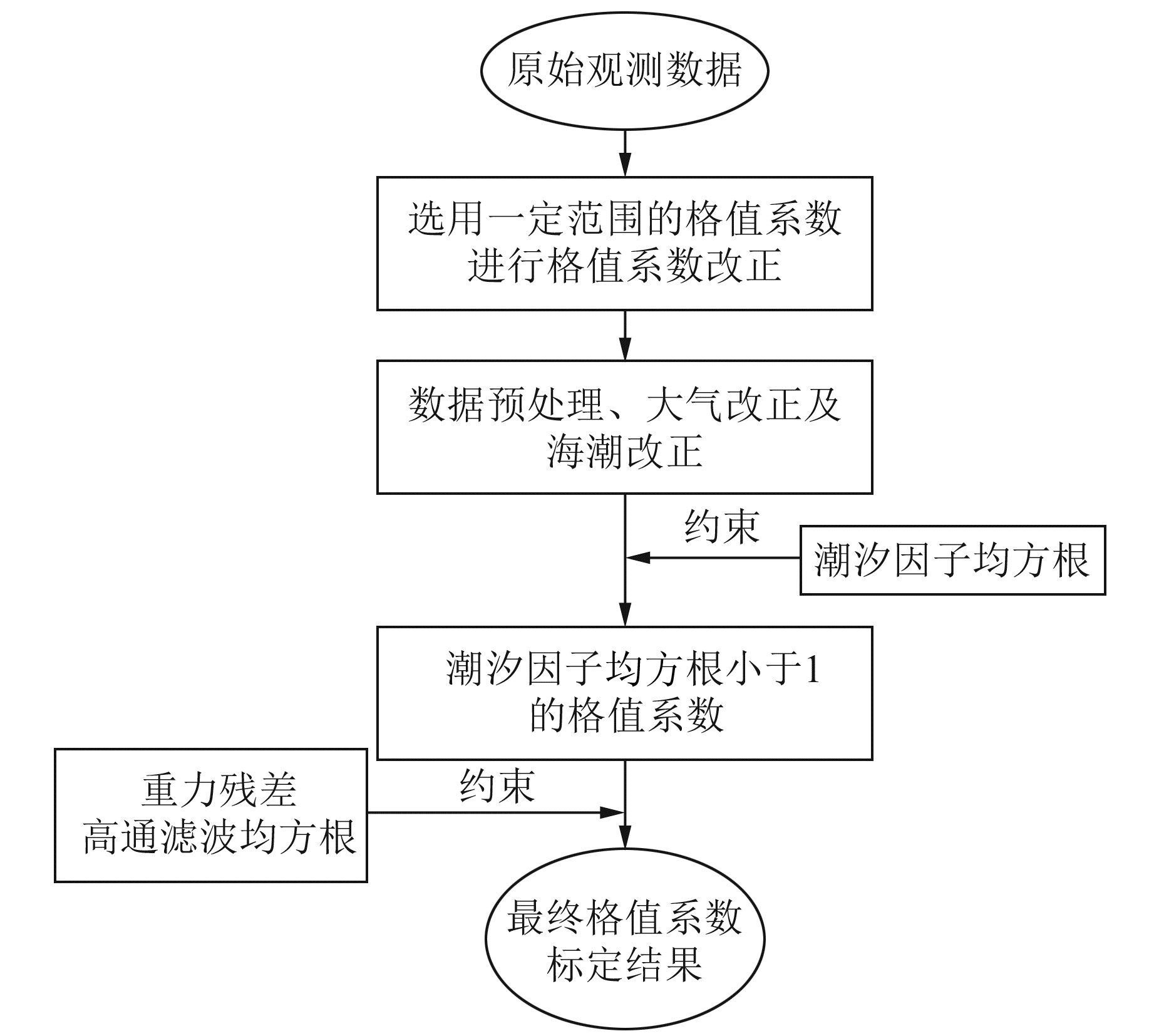
1 数据与格值系数标定本文选用沿海随纬度变化以及由沿海至内陆随经度变化的2条测线共计9个台站2018年的观测资料,使用理论潮汐模型进行约束,对台站gPhone重力仪进行格值系数标定,并使用潮汐因子相对误差、重力残差高通滤波均方根和改正前后的重力残差矢量等指标评定标定结果(图 1)。
|
图 1 格值系数标定流程 Fig. 1 The flow of scale factor calibration |
为去除不同时段地震、台风等因素造成的影响,使最终分析结果能够更好地体现格值系数的空间分布规律,选用大连等9个gPhone连续重力观测台站(沿海台站6个、内陆台站3个)同一时间(2018年)的观测数据。表 1给出了各台站的观测时长和数据完整度。
|
|
表 1 重力台站观测时长与数据完整度 Tab. 1 Observation duration and data completeness of gravity stations |
受到地震、降水、环境噪声等因素的影响,观测数据中可能出现偏离背景值、粗差较大的情况,并对格值系数的标定结果产生影响。因此,需要对重力数据和气压数据进行预处理:
1) 使用低通滤波器对原始观测数据进行滤波,去除观测数据中的高频部分,得到分钟采样值。为了保证数据修正过程的独立性和正确性,对观测数据按月份分别进行处理[7]。
2) 使用Tsoft软件[8]计算理论固体潮模型,扣除理论固体潮得到观测残差,对观测数据中出现的间断、突跳、阶跃等粗差进行手动改正;然后使用一阶多项式拟合对观测残差进行零漂改正;最后再加回理论固体潮,得到经过预处理后的分钟值数据。
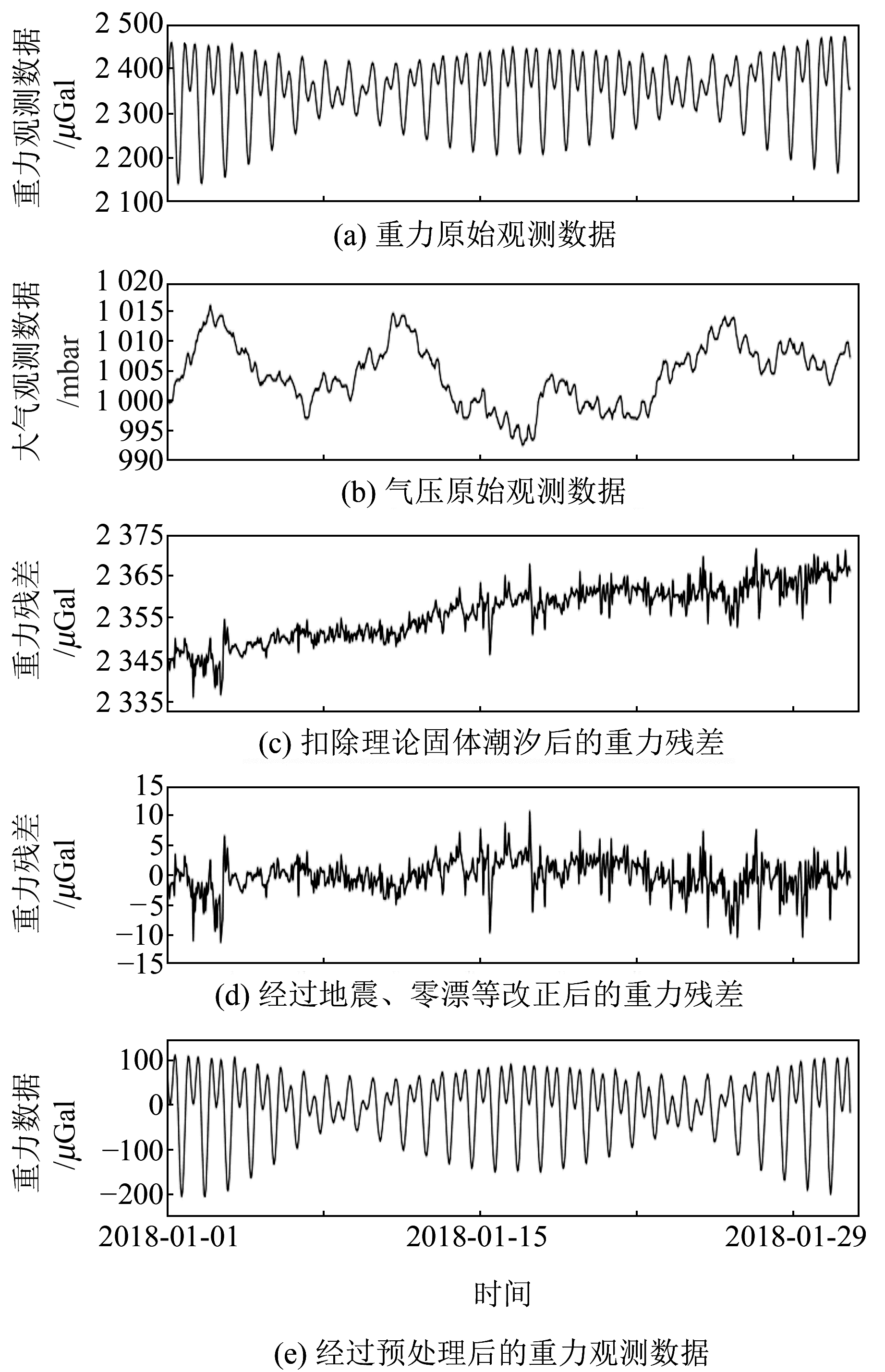
3) 对分钟值数据进行改正后,再次对数据进行降采样处理,得到小时值数据。最后将经过处理的各月小时值数据连接在一起,得到标准格式的数据[9]。图 2给出西安站数据预处理流程。
|
图 2 西安站数据预处理流程 Fig. 2 The data preprocessing flow of Xi'an station |
由于gPhone重力仪在出厂前一般都经过标定,在投入使用后的格值系数标定结果均在1.009 2±0.004范围内[1],因此本文采用范围为0.9~1.1、步长为0.001的一系列格值系数分别对数据进行处理。
对经过格值系数改正后的观测数据进行大气改正以及海潮改正:
| $ g_{\mathrm{re}}=g_{\mathrm{obs}} f-g_{\mathrm{th}}-a a_{\mathrm{st}}-g_{\mathrm{otl}} $ | (1) |
式中,gre为大气改正与海潮改正后的残差值,gobs为经过预处理后的原始数据,f为重力仪的格值系数,a为大气导纳值,ast为仪器测得的大气压值,gth为理论固体潮重力潮汐,gotl为计算得到的海潮重力负荷。
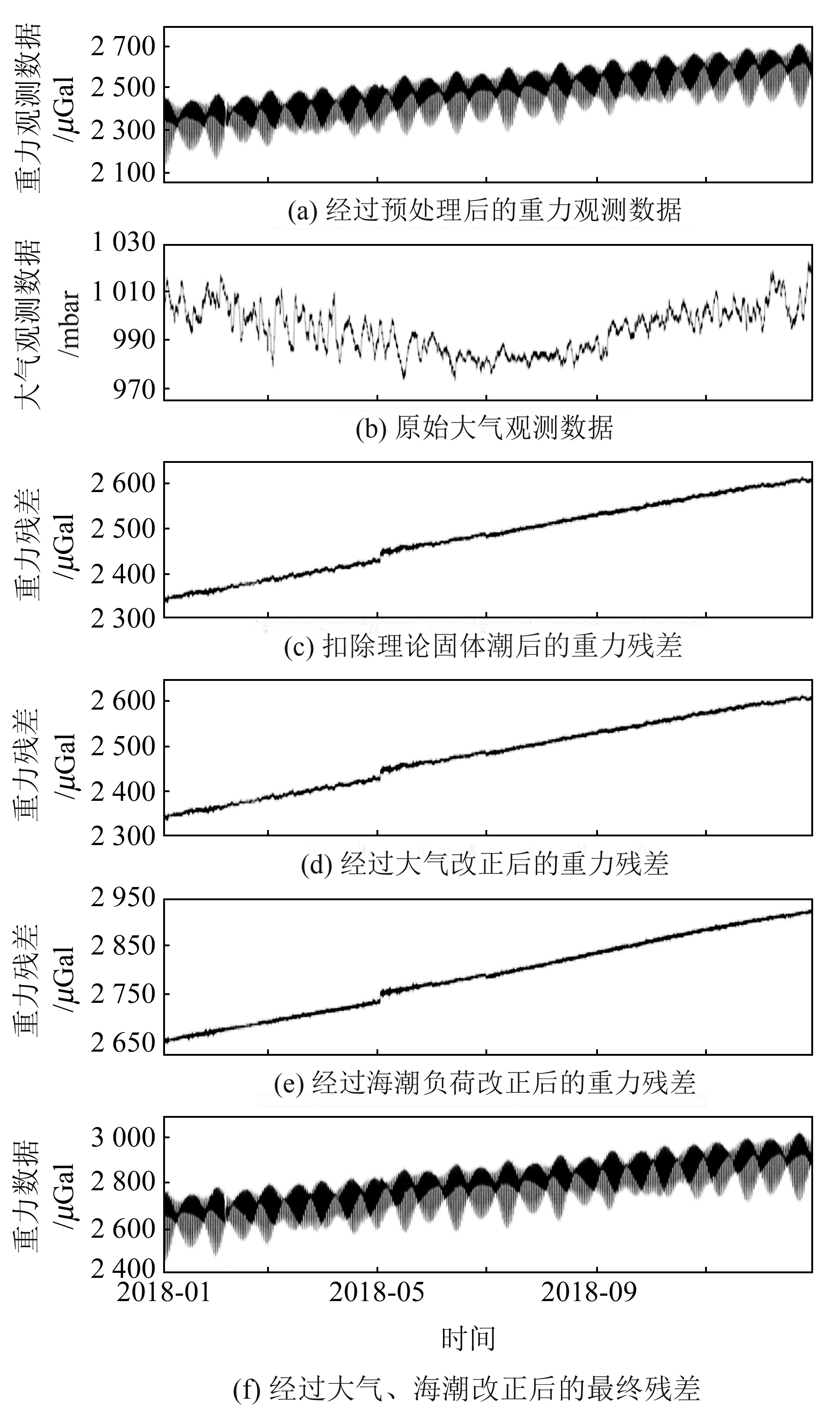
采用移去-恢复法[7]进行改正:1)使用原始重力值乘以格值系数得到实测重力潮汐值,然后使用Tsoft计算DDW理论固体潮模型重力潮汐模拟信号,在实测重力潮汐变化中扣除理论潮汐信号得到残差;2)利用Tsoft人机交互界面对残差进行改正,包括去除尖峰、阶跃、掉格和地震等干扰信号的影响,得到改正残差;3)采用理论大气导纳值(-3.4×10-9 m/(s2 ·hPa))对得到的残差进行大气改正,然后再恢复扣除的DDW理论重力潮汐信号,得到经过第1次处理后的重力潮汐信号;4)使用ETERNA软件[10]对得到的重力潮汐信号进行调和分析,得到重力潮汐的潮波调和参数,即重力合成潮;5)利用得到的合成潮潮汐参数作为模型潮汐参数,重复步骤1)~2),求得观测残差,并与大气信号作联合回归分析,得到大气导纳值a;6)采用新的大气导纳值进行大气改正;7)使用海潮计算软件SPOTL[11],选用全球模型为FES2004、近海模型为osu.chinasea.2010的组合海潮模型计算海潮在台站引起的海潮重力负荷效应,随后扣除海潮负荷引起的重力影响,得到观测重力残余;8)将合成重力潮汐模型加回,得到经过改正之后的重力观测数据(图 3)。
|
图 3 西安站数据处理流程 Fig. 3 The data processing flow of Xi'an station |
传统的以M2潮波为约束的标定方法仅考虑振幅最大的M2潮波带来的影响。其对经过预处理之后的观测数据进行潮汐分析,得到M2潮波的潮汐因子,随后使用理论潮汐模型(如DDW固体潮模型)M2潮波潮汐因子对观测数据进行改正,将二者的比值作为格值系数[3]:
| $ f_{\mathrm{M}_2}=\delta_{\mathrm{DDW}} / \delta_{\mathrm{M}_2} $ | (2) |
式中,fM2为格值系数,δDDW为DDW模型M2潮波潮汐因子,δM2为观测数据M2潮波潮汐因子。
M2潮波标定法步骤简单,但由于忽略了其他振幅较大的潮波对大陆的影响,因此得到的格值系数结果存在一定误差。本文在M2潮波标定法的基础上,充分考虑振幅较大的6个潮波(O1、P1、K1、N2、M2、S2)对观测数据产生的影响,并以此为约束对格值系数进行标定。改进方法主要分2步进行:
1) 基于潮汐因子均方根(factor RMS, FRMS) 确定格值系数范围。使用FRMS评价理论潮汐模型DDW和经过改正之后的观测固体潮之间的各潮波累积误差:
| $ \begin{aligned} \mathrm{FRMS}= & \left\{\sum _ { i = 1 } ^ { I } \left[\left(\delta_m A_0 \cos \varphi_m-\delta_0 A_0 \cos \varphi_0\right)^2+\right.\right. \\ & \left.\left.\left(\delta_m A_0 \sin \varphi_m-\delta_0 A_0 \sin \varphi_0\right)^2\right]\right\} \end{aligned} $ | (3) |
式中,δ0、A0和φ0分别为理论固体潮模型的振幅因子、理论振幅和理论相位(0°),δm和φm分别为实测数据经过大气和固体潮改正之后的振幅因子和相位,I为潮波的分波数量。
使用ETERNA软件对经过格值系数、大气、海潮改正之后的数据进行潮汐调和分析,得到各重力站不同格值系数下的潮汐因子;然后利用式(3)计算不同格值系数各潮波累积均方根;最后筛选FRMS最小区间的格值系数作为均方根检验的结果[6]。表 2为经过均方根检验后的格值系数取值范围。
|
|
表 2 经过均方根检验后的格值系数取值范围 Tab. 2 Value range of scale factors after RMS test |
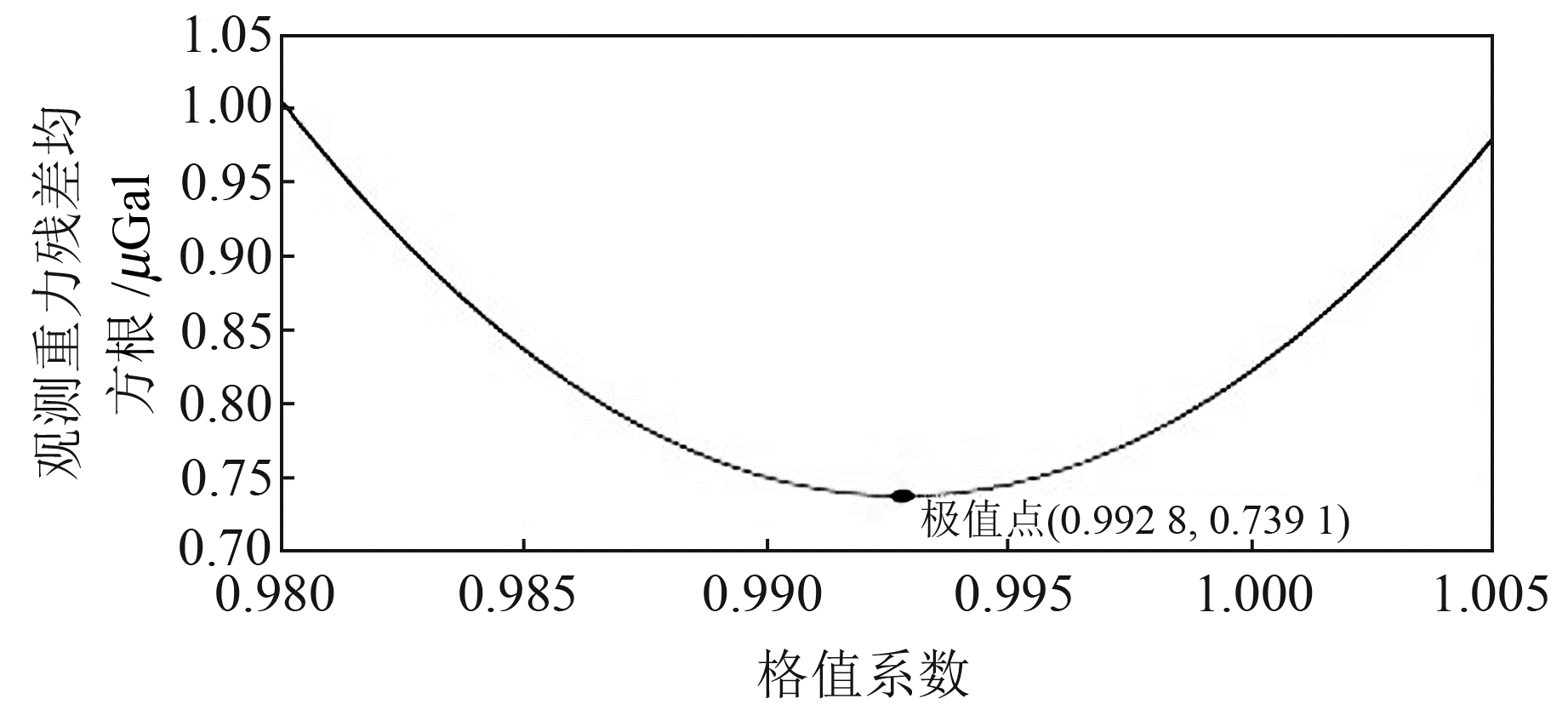
2) 基于重力残差均方根选定最优格值系数。经过均方根检验之后,进一步对格值系数标定结果进行检验。为分析观测数据的半日波和周日波信号,选用潮汐周日波最高频率1.000 CPT作为截止频率进行高通滤波,得到观测重力残差高通滤波值,之后计算重力残差高通滤波值的均方根,即为gPhone重力仪的观测数据精度,最终得到格值系数与观测重力残差均方根一一对应的结果(图 4)。
|
图 4 西安台格值系数与观测重力残差均方根 Fig. 4 RMS of observed gravity residuals and scale factor at Xi'an station |
由图 4可以看出,格值系数和重力残差均方根存在二次函数对应关系,重力残差均方根先随着格值系数的增加而减小,在到达一个最小值后随着格值系数的增大而增大。因此,格值系数存在一个极值使得重力残差均方根值最小。对该二次函数进行求导得出其极值,对应的格值系数即为固体潮模型约束下的标定结果(表 3)。
|
|
表 3 格值系数标定结果 Tab. 3 Results of scale factor calibration |
采用时间域内改正的方法,使用经过检验之后的格值系数标定结果对预处理数据进行改正;之后进行大气改正与海潮改正,得到改正后的固体潮重力信号;再对这些信号进行调和分析,得到经过改正后的观测重力数据振幅因子和相位。为验证格值系数标定结果的准确性,将改正得到的潮汐因子与理论固体潮模型DDW进行对比,其中DDW模型是由Dehant等[12]提出的使用PREM地球模型[13]计算出的流体非静力非弹性地球潮汐模型。采用(观测改正结果-DDW固体潮模型)/观测改正结果的比值来计算相对误差,并以此评价标定结果的精度。表 4给出各台站观测模型M2潮波潮汐因子、中误差以及与DDW模型之间的相对误差。
|
|
表 4 各台站标定结果相对误差 Tab. 4 Relative error of calibration results for each station |
可以看出,经过格值系数、大气改正、海潮改正之后,各台站M2潮波因子潮波中误差在0.000 4~0.001 2之间,说明本文所使用的台站gPhone重力仪观测精度已经接近早期超导重力仪的水平[6]。比较经过格值系数标定前后的潮汐因子与DDW模型之间的相对误差可以看出,经过格值系数改正之前的M2潮波平均相对误差为0.590 1%,而经过格值系数改正之后,M2潮波平均相对误差为0.215 2%。经过格值系数改正,M2潮波潮汐因子的精度有显著提高。
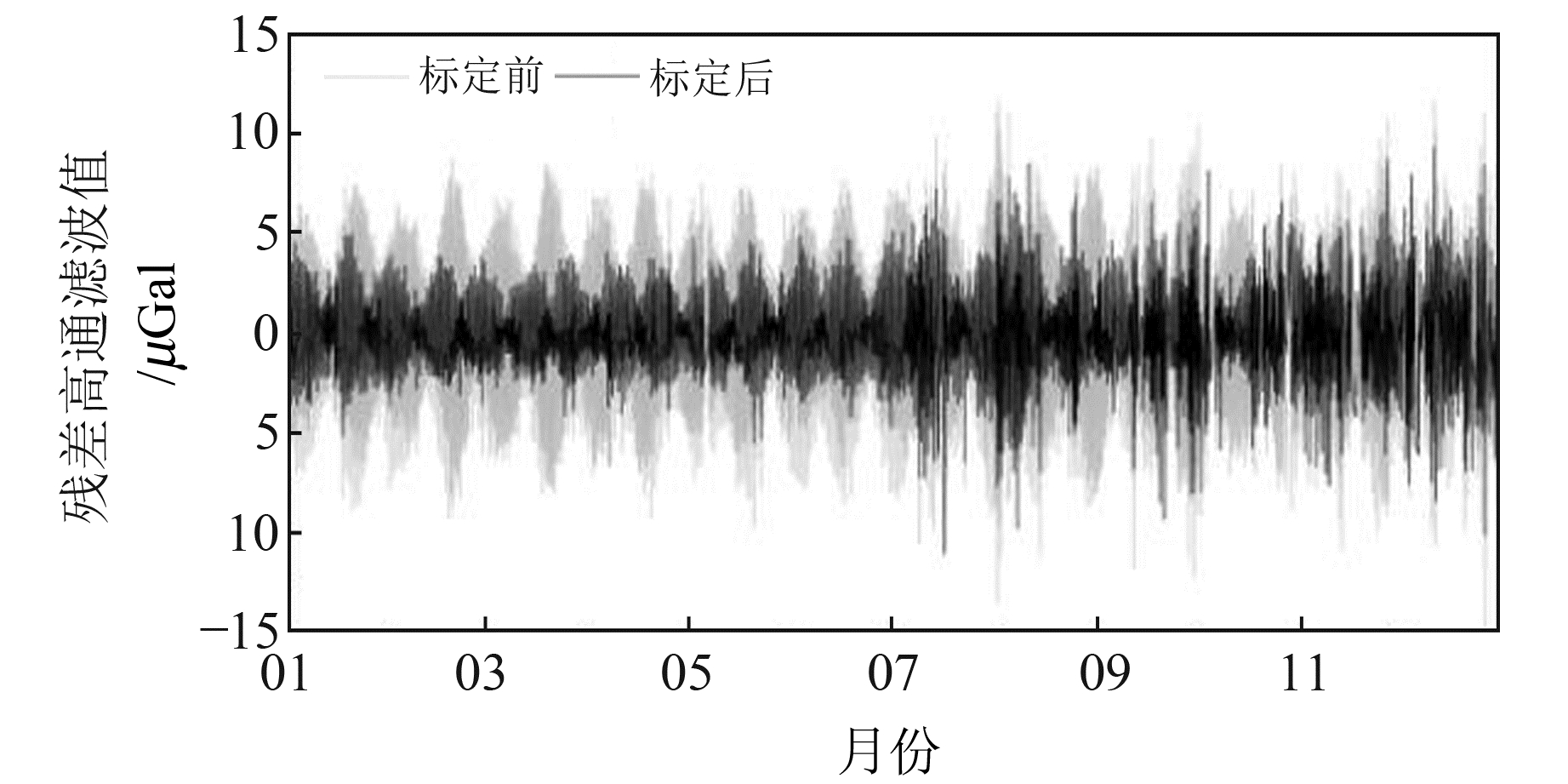
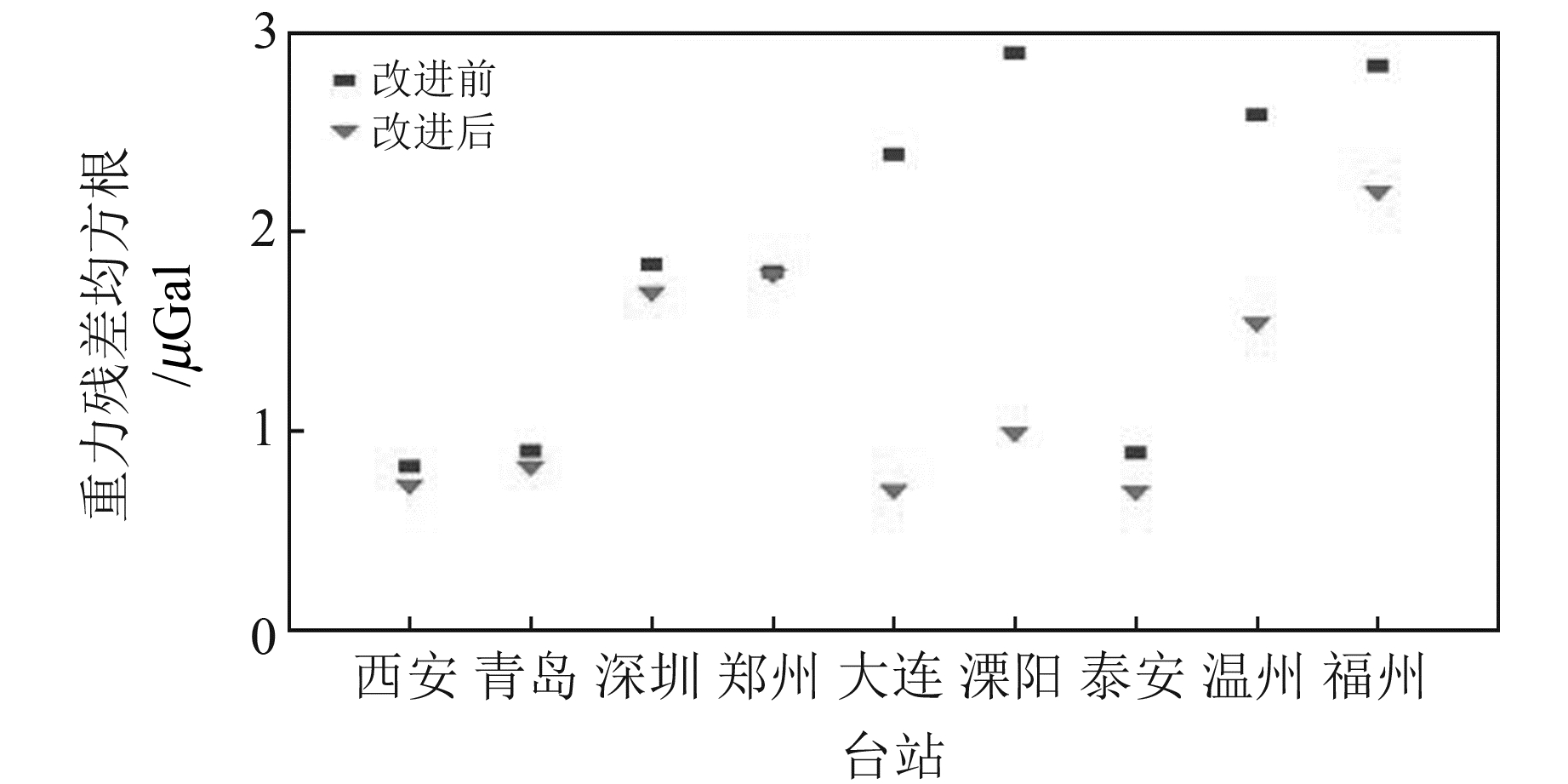
2.2 标定前后残差振幅比较对gPhone重力仪格值系数标定前后的观测数据分别扣除固体潮、大气、海潮、仪器漂移项得到重力残差,然后进行振幅频谱分析,以频率1.000 CPT作为截止频率进行高通滤波得到残差振幅谱。图 5为西安站标定前后残差振幅高通滤波频率谱,图 6为9个台站标定前后重力残差均方根。
|
图 5 西安站格值系数标定前后残差高通滤波振幅谱 Fig. 5 Residual high-pass filtered amplitude spectrum before and after scale factor calibration at Xi'an station |
|
图 6 9个台站经过格值系数改正前后重力残差均方根 Fig. 6 The RMS of gravity residuals before and after correction of scale factors at nine stations |
由图 5可知,在标定之前,西安站的重力残差高通滤波值分布在7 μGal左右;经过格值系数改正之后,重力残差明显降低,高通滤波值分布在4 μGal左右。
从图 6看出,经过格值系数改正之后,各台站的残差振幅都明显减小,且均在2.5 μGal以下,均值为1.690 2 μGal,与韦进等[3]使用FG5绝对重力仪比测方法得到的2 μGal的精度相当。改正之后的残差振幅平均降低15%,其中溧阳站格值系数改正效果最明显,残差降低58.68%。
2.3 标定前后重力残差与残余矢量比较将重力台站按照经度大小自西向东排序,计算海潮改正前后的重力残差矢量和重力残余矢量,并与M2潮波标定法结果进行对比(表 5)。
|
|
表 5 台站经纬度与重力残差/残余矢量 Tab. 5 Gravity residual vector and latitudes and longitudes of the stations |
从表 5中可以看出,本文使用以潮汐模型为约束的标定方法的结果不仅符合重力残差矢量由于海潮影响而出现的随经度自西向东逐渐减小的特征,同时也符合由于海潮负荷改正导致重力残余矢量小于重力残差矢量的规律。M2潮波标定法虽然也满足重力残差随经度变化的规律,但是出现了海潮改正后重力残余矢量大于改正前重力残差矢量的现象,改正结果不符合海潮负荷改正规律。因此,本文使用的以潮汐模型为约束的标定法要优于M2潮波标定法的结果,且标定结果能用于我国大陆海潮负荷相关研究。
综上所述,经过格值系数标定之后,gPhone重力仪观测数据M2潮波潮汐因子的中误差在0.000 4~0.001 2之间,与DDW模型之间的相对误差也提高了68.82%,达到0.215 2%;同时,观测重力残差振幅高通滤波值均方根平均降低15%,数据精度和质量明显提高。标定结果符合我国大陆重力残差矢量自西向东逐渐减小的分布规律,也符合海潮负荷改正后重力残余矢量减小的规律,改正结果优于M2潮波标定法。
3 结语本文以潮汐模型为约束,提出一种改进的gPhone重力仪格值系数标定方法,并以9个台站的gPhone重力仪数据为例验证该方法的精度,主要得到如下结论:
1) 本文使用潮汐模型作为约束对格值系数进行标定,标定之后的潮汐因子与DDW模型潮汐因子相对误差平均为0.215 2%,精度相比标定前提高68.82%;重力残差振幅均方根均在2.5 μGal以下,均值为1.690 2 μGal,相对于改进前平均降低15%。
2) 本文改正结果符合大陆重力残差分布规律以及海潮负荷改正规律,且优于M2潮波标定法改正结果。
3) 本文使用的以潮汐模型作为约束的格值系数标定方法不仅可以在不依赖AG或SG数据比测的情况下对仪器进行标定,且标定后的潮汐因子中误差和残差振幅都符合实际科研工作需要,同时也可以在统一的潮汐基准下对仪器进行标定,为地震监测、重力观测等科学研究提供支持。
| [1] |
刘子维, 李辉, 韦进, 等. 利用M2潮波振幅因子精密测定gPhone弹簧重力仪的标定因子[J]. 大地测量与地球动力学, 2011, 31(5): 146-150 (Liu Ziwei, Li Hui, Wei Jin, et al. Accurate Determination of Calibration Factor of gPhone Spring Gravimeters by Using M2 Tidal Wave Amplitude Factor[J]. Journal of Geodesy and Geodynamics, 2011, 31(5): 146-150)
(  0) 0) |
| [2] |
韦进, 郝洪涛, 韩宇飞, 等. 陆态网络连续重力站近期潮汐观测精度讨论[J]. 中国地震, 2020, 36(4): 888-898 (Wei Jin, Hao Hongtao, Han Yufei, et al. The Discussion on Recent Tidal Data Accuracy by Continuous Gravity Observation Stations in CMONOC[J]. Earthquake Research in China, 2020, 36(4): 888-898)
(  0) 0) |
| [3] |
韦进, 胡敏章, 申重阳, 等. gPhone重力仪绝对标定方法研究[J]. 华中科技大学学报: 自然科学版, 2022, 50(9): 41-47 (Wei Jin, Hu Minzhang, Shen Chongyang, et al. Study on Absolute Calibration Method of gPhone Gravimeter[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2022, 50(9): 41-47)
(  0) 0) |
| [4] |
Francis O, Hendrickx M. Calibration of the LaCoste-Romberg 906 by Comparison with the Superconducting Gravimeter C021 in Membach(Belgium)[J]. Journal of the Geodetic Society of Japan, 2001, 47(1): 16-21
(  0) 0) |
| [5] |
孙和平, 陈晓东, 许厚泽, 等. GWR超导重力仪潮汐观测标定因子的精密测定[J]. 地震学报, 2001, 23(6): 651-658 (Sun Heping, Chen Xiaodong, Xu Houze, et al. Accurate Determination of Calibration Factor for Tidal Gravity Observation of a GWR Superconducting Gravimeter[J]. Acta Seismologica Sinica, 2001, 23(6): 651-658 DOI:10.3321/j.issn:0253-3782.2001.06.011)
(  0) 0) |
| [6] |
韦进, 郝洪涛, 张晓彤, 等. 利用中国北部连续重力站资料评估全球潮汐模型精度[J]. 地震学报, 2021, 43(1): 84-99 (Wei Jin, Hao Hongtao, Zhang Xiaotong, et al. Accuracy Estimation of Global Tide Models Using Continuous Gravity Observation Data in Northern China[J]. Acta Seismologica Sinica, 2021, 43(1): 84-99)
(  0) 0) |
| [7] |
孙和平, 许厚泽, 陈武, 等. 香港地区重力固体潮和海潮负荷特征研究[J]. 地球物理学报, 2006, 49(3): 724-734 (Sun Heping, Xu Houze, Chen Wu, et al. Study of Earth's Gravity Tide and Oceanic Loading Characteristics in Hong Kong Area[J]. Chinese Journal of Geophysics, 2006, 49(3): 724-734)
(  0) 0) |
| [8] |
Camp M, Vauterin P. Tsoft: Graphical and Interactive Software for the Analysis of Time Series and Earth Tides[J]. Computers and Geosciences, 2005, 31(5): 631-640 DOI:10.1016/j.cageo.2004.11.015
(  0) 0) |
| [9] |
陈晓东, 孙和平. 一种新的重力潮汐数据预处理和分析方法[J]. 大地测量与地球动力学, 2002, 22(3): 83-87 (Chen Xiaodong, Sun Heping. New Method for Pre-Processing and Analyzing Tidal Gravity Observations[J]. Journal of Geodesy and Geodynamics, 2002, 22(3): 83-87)
(  0) 0) |
| [10] |
Wenzel H. The Nanogal Software: Earth Tide Data Processing Package ETERNA 330[J]. Bull Inf Marées Terrestres, 1996, 124: 9 425-9 439
(  0) 0) |
| [11] |
Agnew D C. NLOADF: A Program for Computing Ocean-Tide Loading[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5 109-5 110
(  0) 0) |
| [12] |
Dehant V, Defraigne P, Wahr J M. Tides for a Convective Earth[J]. Journal of Geophysical Research: Solid Earth, 1999, 104(B1): 1 035-1 058
(  0) 0) |
| [13] |
Dziewonski A M, Anderson D L. Preliminary Reference Earth Model[J]. Physics of the Earth and Planetary Interiors, 1981, 25(4): 297-356
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


