重力匹配惯性导航是实现水下运载体长时间高精度导航定位的重要手段之一,能有效减弱惯性导航系统(inertial navigation system,INS)随时间推移产生的误差累积[1]。水下重力匹配惯性导航精度依赖于INS精度、水下重力传感器测量精度、重力异常基准图精度以及匹配算法等要素,其中,匹配算法是核心,主要包括基于相关分析技术的地形轮廓匹配(terrain contour matching,TERCOM)算法、迭代最近等值线点(iterated closest contour point,ICCP)算法和基于递推滤波技术的桑迪亚惯性地形辅助导航(Sandia inertial terrain aided navigation,SITAN)算法[2]等。近年来,有学者提出矢量匹配算法[3]、粒子滤波算法[4]、具有约束条件的匹配算法[5]和三角形约束算法[6]等。SITAN算法综合了卡尔曼滤波(Kalman filter,KF)技术和地形随机线性化技术,具有实时性好、可操作性强等特点,在量测值不含粗差且量测误差服从正态分布时能够求得最优无偏估值,但在实际情况下可能出现异常观测值和动力学模型误差等问题,严重时甚至会导致滤波发散。为此,学者们提出多种针对动力学模型误差[7-10]和观测粗差[11-12]的算法,取得了较好的效果。
本文在SITAN算法的基础上,提出一种基于抗差自适应扩展卡尔曼滤波(robust adaptive extended Kalman filter,RAEKF) 的SITAN算法,针对IMU运动学模型误差问题,计算自适应因子调节状态预测协方差矩阵;在此基础上,针对自适应因子的失效问题,通过求解抗差因子剔除粗差;最后利用重力异常模型数据开展仿真实验。
1 SITAN算法数学模型SITAN算法首先根据惯导指示位置,在重力异常模型中得到该处的重力异常值;然后利用搭载的水下重力传感器测量得到运载体航行位置处的真实重力异常值,将二者的差值作为Kalman滤波的量测输入;最后结合惯导误差方程和重力异常随机线性化技术,构建状态方程和量测方程。
1.1 状态方程汪凤林等[13]对重力匹配惯性导航系统的可观测性进行研究,结果表明,系统状态量需要取平面位置误差。基于此,本文取水下运载体的平面位置误差X=(δφ, δλ)T作为滤波状态量,δφ、δλ分别为纬度、经度误差。
INS位置误差微分方程为:
| $ \left[\begin{array}{l} \delta \dot{\varphi} \\ \delta \dot{\lambda} \end{array}\right]=\left[\begin{array}{ccccc} 0 & 0 & -\frac{v_N}{\left(R_M+h\right)^2} & 0 & \frac{1}{R_M+h} \\ \frac{v_E \sec \varphi \tan \varphi}{R_N+h} & 0 & -\frac{v_E \sec \varphi}{\left(R_M+h\right)^2} & \frac{\sec \varphi}{R_N+h} & 0 \end{array}\right]\left[\begin{array}{l} \delta \varphi \\ \delta \lambda \\ \delta h \\ \delta v_E \\ \delta v_N \end{array}\right] $ | (1) |
式中,δvN、δvE分别为N、E向的速度误差,RM、RN分别为子午圈、卯酉圈曲率半径,δφ、δλ和δh分别为纬度、经度和高度误差。
若不考虑速度误差和高度误差的影响,式(1)可简化为:
| $ \left[\begin{array}{l} \dot{\delta} \varphi \\ \dot{\delta \dot{\lambda}} \end{array}\right]=\left[\begin{array}{cc} 0 & 0 \\ \frac{v_E \sec \varphi \tan \varphi}{R_N+h} & 0 \end{array}\right]\left[\begin{array}{l} \delta \varphi \\ \delta \lambda \end{array}\right] $ | (2) |
令
| $ \boldsymbol{F}=\left[\begin{array}{cc} 0 & 0 \\ \frac{v_E \sec \varphi \tan \varphi}{R_N+h} & 0 \end{array}\right] $ | (3) |
则式(2)可表示为:
| $ \dot{\boldsymbol{X}}=\boldsymbol{F} \boldsymbol{X}+\boldsymbol{W} $ | (4) |
对式(3)进行离散化,得到SITAN算法的滤波状态方程:
| $ \boldsymbol{X}_k=\boldsymbol{\varPhi}_{k / k-1} \boldsymbol{X}_{k-1}+\boldsymbol{W}_{k-1} $ | (5) |
式中,Φk/k-1为一步转移矩阵,Φk/k-1=I+F(tk-1)Ts,Ts为离散化时间间隔,Xk、Xk-1分别为k、(k-1)时刻的状态向量,Wk-1为(k-1)时刻的状态噪声。
1.2 量测方程采用SITAN算法进行匹配时,首先要建立重力异常与状态位置的线性关系,即重力异常随机线性化。在量测更新时刻,对水下运载体航行位置(φ, λ)处的真实重力异常在惯导指示位置(φi, λi)处进行一阶泰勒级数展开:
| $ \begin{gathered} \Delta g(\varphi, \lambda)=\Delta g_M\left(\varphi_i, \lambda_i\right)+ \\ \frac{\partial \Delta g_M}{\partial \varphi_i}\left(\varphi-\varphi_i\right)+\frac{\partial \Delta g_M}{\partial \lambda_i}\left(\lambda-\lambda_i\right)+v_i \end{gathered} $ | (6) |
式中,Δg(φ, λ)为水下运载体航行位置处的真实重力异常,ΔgM(φi, λi)为根据惯导指示位置在重力异常基准图上读取的重力异常,∂ΔgM/∂φi为邻域内重力异常纬向梯度,∂ΔgM/∂λi为邻域内重力异常径向梯度,vi为泰勒级数展开过程中的截断误差和重力异常基准图误差。
水下运载体真实位置处的重力异常可表示为实测重力异常与量测噪声之和:
| $ \Delta g(\varphi, \lambda)=\Delta g_s\left(\varphi_t, \lambda_t\right)+v_s $ | (7) |
式中,Δgs(φt, λt)为水下运载体实际观测重力异常,vs为水下重力传感器量测噪声。
由式(6)和式(7)可得:
| $ \begin{aligned} & \Delta g_M\left(\varphi_i, \lambda_i\right)-\Delta g_s\left(\varphi_t, \lambda_t\right)= \\ & \frac{\partial \Delta g_M}{\partial \varphi_i} \delta \varphi+\frac{\partial \Delta g_M}{\partial \lambda_i} \delta \lambda+v_i-v_s \end{aligned} $ | (8) |
令
| $ \left\{\begin{array}{l} \boldsymbol{H}_k=\left[\frac{\partial \Delta g_M}{\partial \varphi_i}, \frac{\partial \Delta g_M}{\partial \lambda_i}\right] \\ \boldsymbol{V}_k=\boldsymbol{v}_i-\boldsymbol{v}_s \end{array}\right. $ | (9) |
整理式(9)可得SITAN算法的滤波量测方程为:
| $ \boldsymbol{Z}_k=\boldsymbol{H}_k \boldsymbol{X}_k+\boldsymbol{V}_k $ | (10) |
SITAN算法的滤波递推方程如下:
| $ \left\{\begin{array}{l} \hat{\boldsymbol{X}}_{k / k-1}=\boldsymbol{\varPhi}_{k / k-1} \hat{\boldsymbol{X}}_{k-1} \\ \boldsymbol{P}_{k / k-1}=\boldsymbol{\varPhi}_{k / k-1} \boldsymbol{P}_{k-1} \boldsymbol{\varPhi}_{k / k-1}^{\mathrm{T}}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} \\ \boldsymbol{K}_k=\boldsymbol{P}_{k / k-1} \boldsymbol{H}_k^{\mathrm{T}}\left(\boldsymbol{H}_k \boldsymbol{P}_{k / k-1} \boldsymbol{H}_k^{\mathrm{T}}+\boldsymbol{R}_k\right)^{-1} \\ \hat{\boldsymbol{X}}_k=\hat{\boldsymbol{X}}_{k / k-1}+\boldsymbol{K}_k\left(\boldsymbol{Z}_k-\boldsymbol{H}_k \hat{\boldsymbol{X}}_{k / k-1}\right) \\ \boldsymbol{P}_k=\left(\boldsymbol{I}-\boldsymbol{K}_k \boldsymbol{H}_k\right) \boldsymbol{P}_{k / k-1} \end{array}\right. $ | (11) |
式中,
精确的滤波模型和误差统计特性是卡尔曼滤波最优估计的基础。但在实际的水下组合导航应用中,滤波数学模型与真实模型存在偏差,且观测值会受到外界环境的影响,使得异常观测值的存在不可避免,若直接进行解算将会导致导航解次优甚至滤波发散[14]。为此,本文采用基于RAEKF的SITAN算法,其原理是利用自适应因子和抗差因子调节预测信息和观测信息对滤波结果贡献的权重[15]:
| $ \left\{\begin{array}{l} \overline{\boldsymbol{P}}_{k / k-1}=\frac{1}{\alpha_k} \boldsymbol{P}_{k / k-1} \\ \overline{\boldsymbol{R}}_k=\frac{1}{r_k} \boldsymbol{R}_k \end{array}\right. $ | (12) |
式中,αk为自适应因子,rk为抗差因子。将式(12)中的
模型误差判别统计量取预测残差统计量,预测残差
| $ \overline{\boldsymbol{V}}_k=\boldsymbol{H}_k \hat{\boldsymbol{X}}_{k / k-1}-\boldsymbol{Z}_k $ | (13) |
预测残差统计量ΔVk和对应的自适应因子αk的计算公式为:
| $ \Delta \bar{V}_k=\left(\frac{\overline{\boldsymbol{V}}_k^{\mathrm{T}} \overline{\boldsymbol{V}}_k}{\operatorname{tr}\left(\boldsymbol{\Sigma}_{\bar{V}_k}\right)}\right)^{\frac{1}{2}} $ | (14) |
| $ \alpha_k=\left\{\begin{array}{l} 1, \left|\Delta \bar{V}_k\right| \leqslant c \\ \frac{c}{\left|\Delta \bar{V}_k\right|}, \left|\Delta \bar{V}_k\right|>c \end{array}\right. $ | (15) |
式中,ΣVk为预测残差协方差矩阵,tr(·)为取迹,c为常数,一般取1.5~2.0。
抗差因子选择IGGⅢ函数模型:
| $ r_k=\left\{\begin{array}{l} 1, \left|\nabla \bar{V}_k\right| \leqslant c_0 \\ \frac{c_0}{\left|\nabla \bar{V}_k\right|}\left(\frac{c_1-\left|\nabla \bar{V}_k\right|^2}{c_1-c_0}\right), \\ c_0<\left|\nabla \bar{V}_k\right| \leqslant c_1 \\ 0, \left|\nabla \bar{V}_k\right|>c_1 \end{array}\right. $ | (16) |
式中,c0、c1为常数,分别取1~1.5、3.5~4.5,
| $ \nabla \bar{V}_k=\frac{\overline{\boldsymbol{V}}_k}{\sqrt{\boldsymbol{\Sigma}_{\bar{V}_k}}} $ | (17) |
预测残差只有在观测值不包含粗差的情况下才能反映状态预测信息的异常,即在量测信息可靠的情况下自适应因子才有效。因此,在计算自适应因子之前,应判别观测值是否包含粗差,若包含粗差,则直接选择抗差滤波进行解算;若不包含粗差,则选择自适应滤波进行解算。当预测残差统计量大于阈值时,采用自适应因子抑制IMU运动学推算误差。
基于RAEKF的SITAN算法流程见图 1。
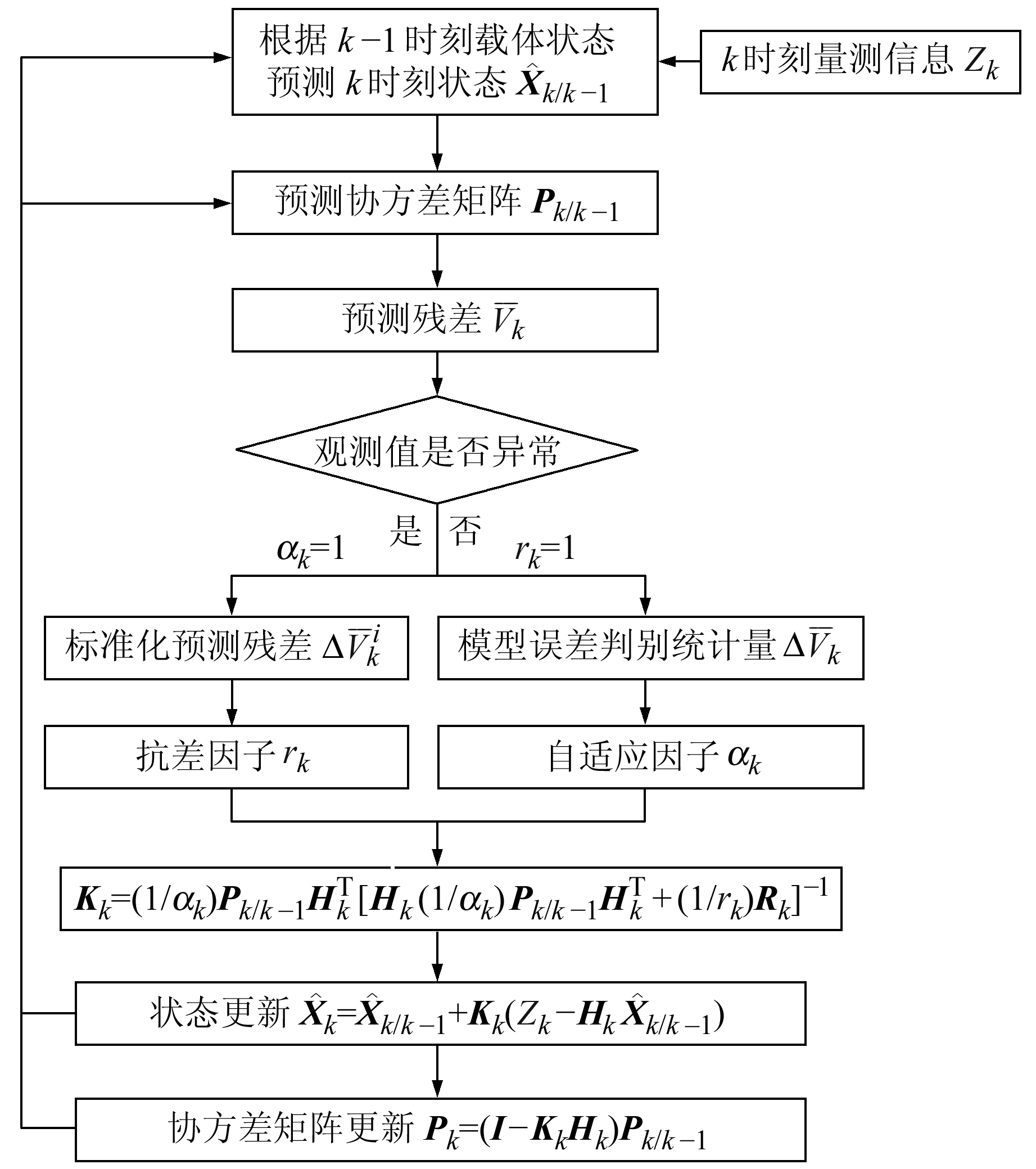
|
图 1 算法流程 Fig. 1 Flow chart of algorithm |
为验证匹配算法的有效性,选取南海一块重力异常变化丰富的海域开展仿真实验。重力异常基准图采用DTU17重力异常模型,分辨率为1'×1',中误差为2~3 mGal。初始状态量为X0=(0, 0)T,P0=10-5I, Qk=0.03I, Rk=0.25。通过在重力异常基准图数据上添加中误差为3 mGal的高斯白噪声,可以得到水下运载体的重力异常观测数据。图 2为实验海域的重力异常三维模型图。
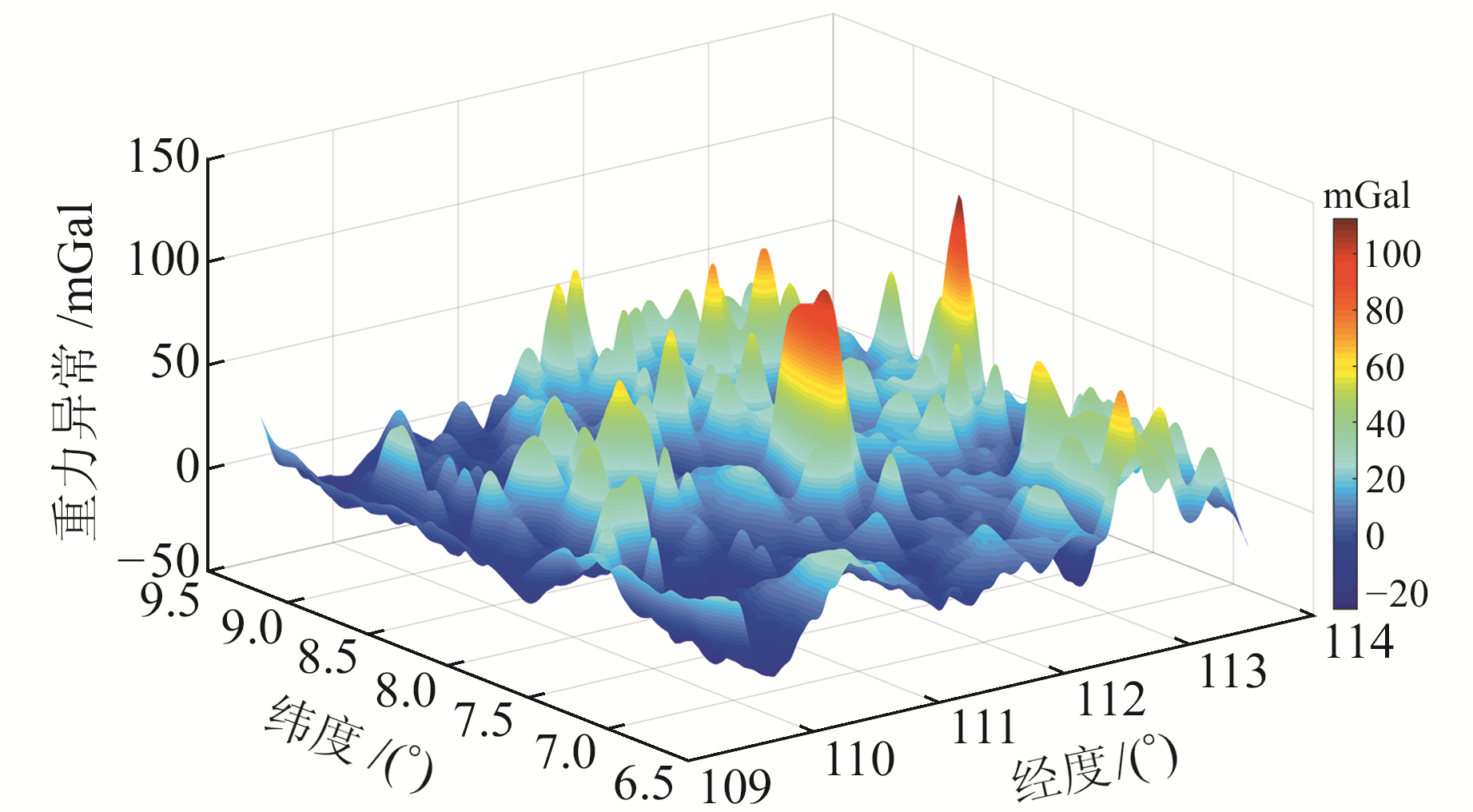
|
图 2 实验海域重力异常三维模型 Fig. 2 3D model of gravity anomaly in the test area |
利用航迹仿真算法生成参考航迹,时长为24 h,初始位置为(7°N,113°E,-100 m),初始速度为(0 m/s,0 m/s,0 m/s),初始姿态为(0°,0°,45°)。本次实验水下运载体真实航迹运动过程如下:首先以0.008 6 m/s2的加速度加速600 s,速度达到10 kn后匀速行驶28 110 s;然后左转45°,匀速行驶28 800 s;最后右转45°,匀速行驶28 890 s。设置惯导采样频率为100 Hz,基于生成的真实航迹,利用捷联惯导反演算法生成航迹上各采样点处的惯性器件输出,即角增量和速度增量。将生成的惯性器件输出表 1所示的误差参数,模拟真实环境下的惯导元器件输出,利用双子样算法进行惯导解算,生成惯导航迹。
|
|
表 1 惯性器件误差参数 Tab. 1 Inertial device error parameters |
结合载体航行速度和重力异常基准图分辨率,设置量测更新间隔为180 s,分别利用常规SITAN算法(EKF算法)和抗差自适应SITAN算法(RAEKF算法)展开重力匹配仿真实验。为对比2种算法的抗差效果,在第160~240次量测更新之间,每隔5次在原始观测值上加入30 mGal的粗差,对应滤波时段为8~12 h。
3.2 常规SITAN算法仿真真实航迹、惯导航迹以及EKF算法匹配航迹见图 3。利用EKF算法处理带有粗差观测值的匹配航迹(EKF-Outlier)、惯导航迹(INS)与EKF算法匹配航迹的位置误差见图 4。由图 3和图 4可知,在观测值未加入粗差的情况下,EKF算法能够有效修正惯导整体航迹,其匹配结果定位精度优于INS精度;在观测值加入粗差的情况下,滤波时长小于8 h,匹配航迹能收敛于真实航迹,观测值加入粗差后,滤波在纬度和经度方向上逐渐发散,导航定位精度与INS精度相当,滤波器失效。
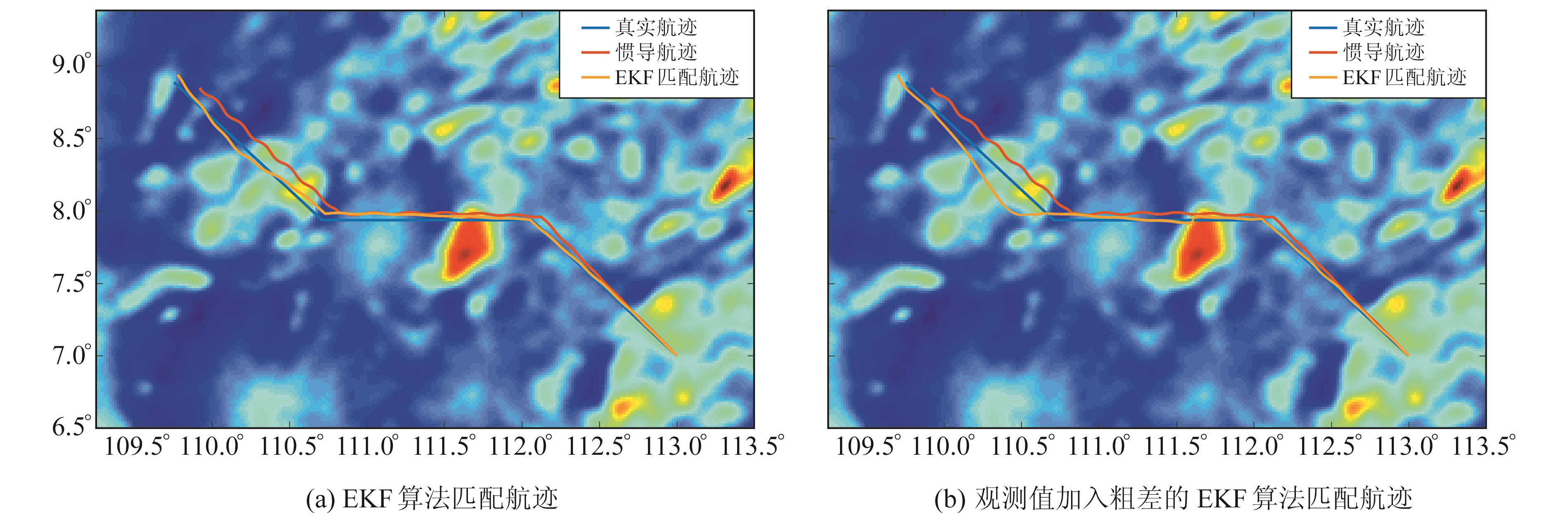
|
图 3 常规SITAN算法匹配航迹 Fig. 3 The matching tracks of ordinary SITAN algorithm |
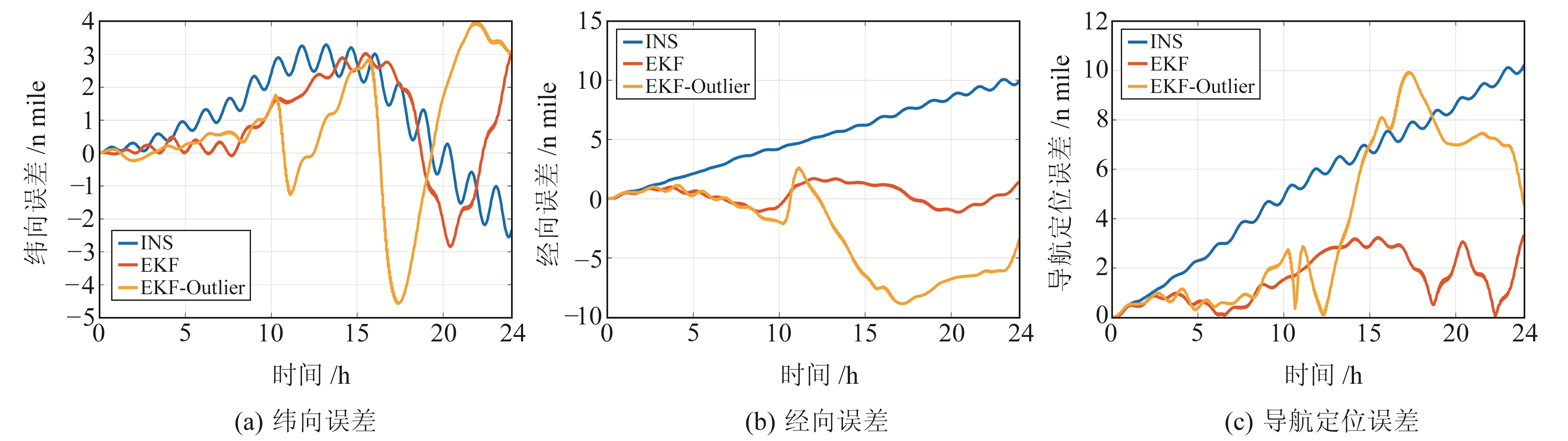
|
图 4 航迹位置误差 Fig. 4 Position error of tracks |
对EKF算法匹配结果的位置误差进行统计,并与INS的位置误差进行对比,结果见表 2(单位n mile)。由表 2可知,观测值存在粗差的情况下,EKF算法导航定位误差最大值为9.93 n mile,RMS为5.01 n mile;INS导航定位误差最大值为10.24 n mile,RMS为6.16 n mile,滤波结果失真。由此可知,EKF算法无法抵抗异常观测值的影响。因此,需要构建自适应因子和抗差因子实现状态预测信息的自适应控制以及粗差剔除。
|
|
表 2 误差统计 Tab. 2 Error statistics |
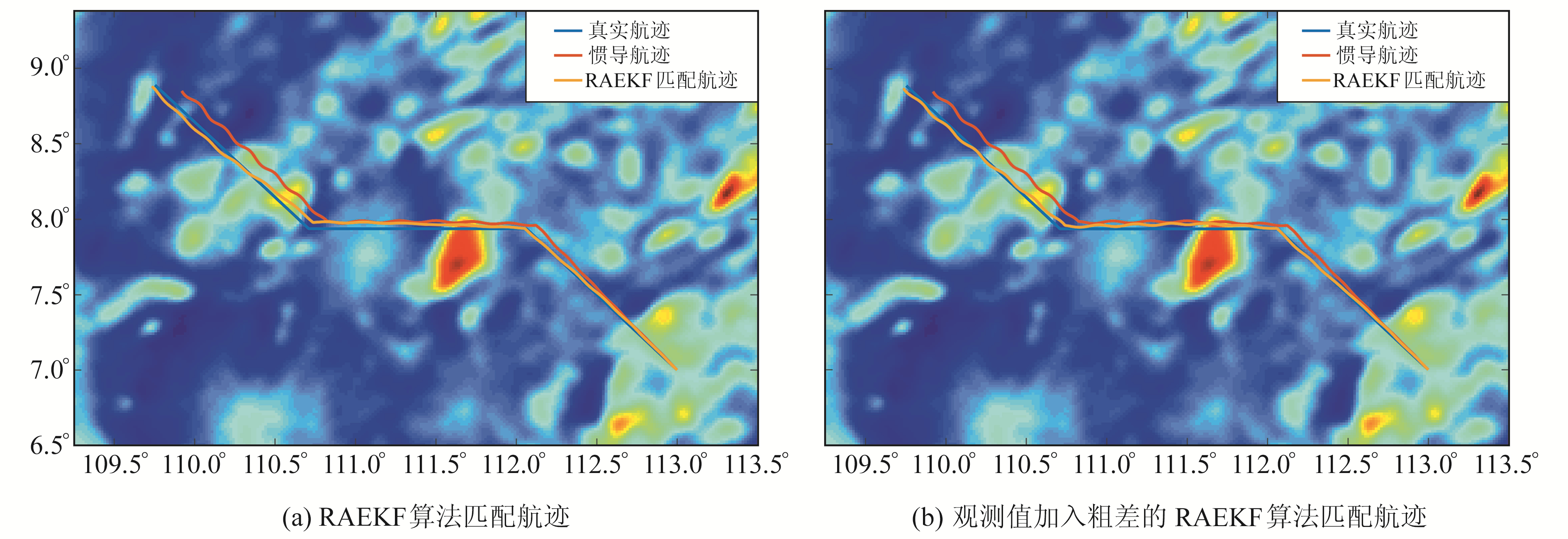
RAEKF算法匹配航迹以及航迹位置误差见图 5和图 6,其中,RAEKF-Outlier为利用RAEKF算法处理带有粗差观测值的匹配航迹。由图 5和图 6可知,在观测值未加入粗差的情况下,RAEKF算法能显著降低惯导累积误差的影响,修正惯导整体轨迹,且RAEKF算法的匹配精度远优于INS。相较于EKF算法,RAEKF算法的导航定位精度也有提升。在观测值加入粗差的情况下,RAEKF算法的效果更加显著。由此可见,在自适应因子和抗差因子的作用下,系统的稳健性和精度均有提高。
|
图 5 基于RAEKF的SITAN算法匹配航迹 Fig. 5 The matching tracks of SITAN algorithm based on RAEKF |

|
图 6 航迹位置误差 Fig. 6 Position error of tracks |
RAEKF算法匹配结果位置误差统计见表 3(单位n mile)。由表 2和表 3可知,在观测值未加入粗差的情况下,RAEKF算法相较于EKF算法的导航定位精度提升了1.6%;在观测值加入粗差的情况下,RAEKF算法相较于EKF算法在纬向和经向上的定位精度分别提高了49.5%和81.6%,整体导航定位精度提高了73.9%,滤波器运行平稳。由此可见,RAEKF算法能有效抑制观测粗差的影响。
|
|
表 3 误差统计 Tab. 3 Error statistics |
针对水下重力匹配导航中存在观测粗差和动力学模型误差的问题,提出一种抗差自适应SITAN算法,并利用重力异常模型数据开展水下重力匹配仿真实验。结果表明,在观测值存在粗差的情况下,抗差自适应SITAN算法的定位精度可达到1.31 n mile,较常规SITAN算法的精度提升73.9%。
| [1] |
欧阳明达, 孙艺轩, 邝英才, 等. 应用抗差估计SITAN算法的水下重力匹配导航方法[J]. 中国惯性技术学报, 2021, 29(2): 214-220 (Ouyang Mingda, Sun Yixuan, Kuang Yingcai, et al. Underwater Gravity Matching Navigation Method of SITAN Algorithm with Robust Estimation[J]. Journal of Chinese Inertial Technology, 2021, 29(2): 214-220)
(  0) 0) |
| [2] |
王傲明, 李姗姗, 李新星, 等. 基于自适应并行扩展卡尔曼滤波的SITAN匹配算法[J]. 中国惯性技术学报, 2022, 30(1): 81-88 (Wang Aoming, Li Shanshan, Li Xinxing, et al. SITAN Matching Algorithm Based on Adaptive Parallel Extended Kalman Filter[J]. Journal of Chinese Inertial Technology, 2022, 30(1): 81-88)
(  0) 0) |
| [3] |
Wang B, Zhu J W, Ma Z X, et al. Improved Particle Filter-Based Matching Method with Gravity Sample Vector for Underwater Gravity-Aided Navigation[J]. IEEE Transactions on Industrial Electronics, 2021, 68(6): 5 206-5 216 DOI:10.1109/TIE.2020.2988227
(  0) 0) |
| [4] |
欧阳明达, 杨元喜. 改进粒子滤波的水下重力匹配导航仿真与实验[J]. 哈尔滨工程大学学报, 2022, 43(10): 1 514-1 521 (Ouyang Mingda, Yang Yuanxi. Underwater Gravity Matching Navigation Simulation and Experiment Based on the Improved Particle Filtering Algorithm[J]. Journal of Harbin Engineering University, 2022, 43(10): 1 514-1 521)
(  0) 0) |
| [5] |
邹嘉盛, 肖云, 孟宁, 等. 一种基于约束条件的重力匹配导航算法[J]. 武汉大学学报: 信息科学版, 2020, 45(10): 1 570-1 577 (Zou Jiasheng, Xiao Yun, Meng Ning, et al. A Gravity Matching Navigation Algorithm Based on Constraint[J]. Geomatics and Information Science of Wuhan University, 2020, 45(10): 1 570-1 577)
(  0) 0) |
| [6] |
Yang Z L, Zhu Z S, Zhao W G. A Triangle Matching Algorithm for Gravity-Aided Navigation for Underwater Vehicles[J]. Journal of Navigation, 2014, 67(2): 227-247 DOI:10.1017/S0373463313000660
(  0) 0) |
| [7] |
杨元喜, 徐天河. 基于移动开窗法协方差估计和方差分量估计的自适应滤波[J]. 武汉大学学报: 信息科学版, 2003, 28(6): 714-718 (Yang Yuanxi, Xu Tianhe. An Adaptive Kalman Filter Combining Variance Component Estimation with Covariance Matrix Estimation Based on Moving Window[J]. Geomatics and Information Science of Wuhan University, 2003, 28(6): 714-718)
(  0) 0) |
| [8] |
杨元喜, 何海波, 徐天河. 论动态自适应滤波[J]. 测绘学报, 2001, 30(4): 293-298 (Yang Yuanxi, He Haibo, Xu Tianhe. Adaptive Robust Filtering for Kinematic GPS Positioning[J]. Acta Geodaetica et Cartographic Sinica, 2001, 30(4): 293-298)
(  0) 0) |
| [9] |
杨元喜, 任夏, 许艳. 自适应抗差滤波理论及应用的主要进展[J]. 导航定位学报, 2013, 1(1): 9-15 (Yang Yuanxi, Ren Xia, Xu Yan. Main Progress of Adaptively Robust Filter with Applications in Navigation[J]. Journal of Navigation and Positioning, 2013, 1(1): 9-15)
(  0) 0) |
| [10] |
高为广, 何海波, 陈金平. 自适应UKF算法及其在GPS/INS组合导航中的应用[J]. 北京理工大学学报, 2008, 28(6): 505-509 (Gao Weiguang, He Haibo, Chen Jinping. An Adaptive UKF Algorithm and Its Application in GPS/INS Integrated Navigation[J]. Journal of Beijing University of Technology, 2008, 28(6): 505-509)
(  0) 0) |
| [11] |
杨元喜. 动态系统的抗差Kalman滤波[J]. 测绘学院学报, 1997, 14(2): 79-84 (Yang Yuanxi. Robust Kalman Filter for Dynamic Systems[J]. Journal of Institute of Surveying and Mapping, 1997, 14(2): 79-84)
(  0) 0) |
| [12] |
杨元喜. 抗差估计理论及其应用[M]. 北京: 八一出版社, 1993 (Yang Yuanxi. Robust Estimation Theory and Its Application[M]. Beijing: Bayi Press, 1993)
(  0) 0) |
| [13] |
汪凤林, 蔡体菁, 王东霞. 惯性/重力匹配组合导航系统可观测性研究[J]. 安徽大学学报: 自然科学版, 2008, 32(6): 27-31 (Wang Fenglin, Cai Tijing, Wang Dongxia. Inertial/Gravity Matching Integrated Navigation System[J]. Journal of Anhui University: Natural Sciences, 2008, 32(6): 27-31)
(  0) 0) |
| [14] |
苗岳旺, 孙付平, 李飞, 等. 基于抗差EKF的INS/GNSS紧组合算法应用研究[J]. 大地测量与地球动力学, 2013, 33(3): 97-101 (Miao Yuewang, Sun Fuping, Li Fei, et al. Research on Application of Tightly Coupled INS/GNSS Based on Robust Extended Kalman Filter[J]. Journal of Geodesy and Geodynamics, 2013, 33(3): 97-101)
(  0) 0) |
| [15] |
高为广, 封欣, 朱大为. 基于神经网络构造的GPS/INS自适应组合导航算法[J]. 大地测量与地球动力学, 2007, 27(2): 64-67 (Gao Weiguang, Feng Xin, Zhu Dawei. GPS/INS Adaptively Integrated Navigation Algorithm Based on Neural Network[J]. Journal of Geodesy and Geodynamics, 2007, 27(2): 64-67)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


