2. 国家海洋局南海调查技术中心,广州市新港西路155号,510300;
3. 中国测绘科学研究院,北京市莲花池西路28号,100036
海洋变化对近海地面高程变化的影响一般包括海潮负荷和非潮汐海洋负荷。海潮负荷对测站位移的影响在某些沿海地区可达数cm[1]。非潮汐海洋负荷是由地表风动力、热量、湿度和大气压变化等环境因素导致的海水质量迁徙造成的负荷。Zerbini等[2]在CORS站的垂向时间序列中发现非潮汐海洋负荷的影响,并且采用格林函数方法,利用ECCO(estimating the circulation and climate of the ocean)海底压力模型计算该影响,计算结果和观测结果具有高相关性。Williams等[3]研究非潮汐海洋负荷和大气负荷对GPS大地高的影响,提出用高分辨率的模型来改正非潮汐海洋负荷对GPS大地高的影响。周伯烨等[4]利用ECCO海底压力模型数据研究非潮汐海洋负荷对近海岸IGS测站坐标时间序列的影响。Munekane等[5]利用海面变化研究赤道太平洋地区的非潮汐海洋负荷影响。还有部分学者利用海底压力数据对地面负荷形变进行计算,获得某些CORS站点的海洋非潮汐负荷形变,同时分析其在GPS非构造形变中的贡献[6-8]。
目前多采用ECCO海底压力模型数据计算非潮汐海洋负荷对形变的影响。但由于ECCO海底压力模型中的误差难以定量,会带入形变分析中[9],而且ECCO和OMCT(ocean model for circulation and tides)2种海底压力模型由于采用不同的海底地形模型,导致差别较大。此外,在计算非潮汐海洋负荷局部影响时,通常采用格林函数积分方法。格林函数方法是一种区域积分方法,不能很好地考虑全球影响。随着卫星测高技术的发展,可以获得高精度的海平面变化数据,为非潮汐海洋负荷计算提供了很好的数据源。
本文基于多源卫星测高数据综合获得的高精度海平面变化数据,利用球谐分析方法,将全球海面高数据建立成全球模型,使数据耦合性更好、在某个区域的计算更为一致,最后分析非潮汐海洋负荷对广东地区地面高程的影响。
1 数据处理全球海平面变化数据采用哥白尼海洋环境监测服务中心(CMEMS)全球海洋物理分析预测模型日变化产品(http://marine.copernicus.eu)。
CMEMS全球海洋物理分析预测模型产品包含非实时产品和近实时产品等多种海平面高产品,高度为正高,融合了多卫星测高数据,全球覆盖格网产品空间分辨率为0.25°×0.25°,时间分辨率为1 d或1月。
根据海平面变化数据,利用负荷球谐分析方法获得全球负荷球谐系数,进而利用负荷形变动力学方程[10]计算负荷相关影响。具体计算步骤如下:
1) 读取数据和转换格式,剔除缺失数据,用“0”替换缺省数据“NaN”,检查其他存在的数据错误。为方便后续计算与分析,将单位转换为mm,将时间与GPS周时间一一对应。
2) 大地纬度数据生成地心纬度数据。由于球谐分析采用地心纬度,因此将原始数据的大地纬度转换为地心纬度。
3) 沿海地区海平面变化数据会与地面土壤水数据产生重叠,使相关计算产生误差,当同时考虑土壤水负荷影响时,应尽量进行陆海分离。陆海分离时,以ETOPO1地形数据为参考标准确定海平面变化数据边界。
4) 选择一定的时间基准,扣除相应的平均值,采用球谐分析方法,将海平面变化等效水高展开成负荷球谐函数的级数[11]。
地面点(R, θ, λ)处等效水高变化hw的规格化负荷球谐展开式为:
| $ \begin{gathered} h_{\mathrm{w}}(R, \theta, \lambda)=R \sum\limits_{n=1}^N \sum\limits_{m=0}^n\left[\Delta C_{m m}^{\mathrm{w}} \cos (m \lambda)+\right. \\ \left.\Delta S_{n m}^{\mathrm{w}} \sin (m \lambda)\right] \bar{P}_{n m}(\cos \theta) \end{gathered} $ | (1) |
式中,R为地球平均半径,ΔCnmw、ΔSnmw为n阶m次规格化负荷球谐系数,
以负荷球谐系数为未知参数,利用转换后的海平面变化等效水高建立观测方程,估计负荷球谐系数。为了提高球谐建模的稳定性和精度,建立观测方程前扣除等效水高的平均值。
5) 利用负荷球谐系数计算非潮汐海洋负荷对大地高和正常高的影响:
| $ \left\{\begin{array}{l} \Delta \bar{C}_{n m}=\frac{3}{2 n+1} \frac{\rho_{\mathrm{w}}}{\rho_{\mathrm{e}}} \Delta C_{n m}^{\mathrm{w}} \\ \Delta \bar{S}_{n m}=\frac{3}{2 n+1} \frac{\rho_{\mathrm{w}}}{\rho_{\mathrm{e}}} \Delta S_{m m}^{\mathrm{w}} \end{array}\right. $ | (2) |
式中,ρw为水的密度,ρe为地球平均密度。由负荷形变理论,非潮汐海洋负荷对地面大地高变化的影响为:
| $ \begin{gathered} \mathrm{d} r=\frac{G M}{\gamma r} \sum\limits_{n=2}^{\infty}\left(\frac{a}{r}\right)^n h_n^{\prime} \sum\limits_{m=0}^n\left(\Delta \bar{C}_{n m} \cos (m \lambda)+\right. \\ \left.\Delta \bar{S}_{n m} \sin (m \lambda)\right) \bar{P}_{n m}(\cos \theta) \end{gathered} $ | (3) |
对地面正常高变化的影响为:
| $ \begin{gathered} \mathrm{d} r^{\prime}=\frac{G M}{\gamma r} \sum\limits_{n=2}^{\infty}\left(\frac{a}{r}\right)^n\left(h_n^{\prime}-1-k_n^{\prime}\right) \cdot \\ \sum\limits_{m=0}^n\left(\Delta \bar{C}_{n m} \cos (m \lambda)+\Delta \bar{S}_{m n} \sin (m \lambda)\right) \bar{P}_{n m}(\cos \theta) \end{gathered} $ | (4) |
式中,h'n为n阶径向负荷数,k'n为n阶位负荷数。
2 非潮汐海洋负荷对大地高的影响 2.1 数据预处理使用2018~2020年的CMEMS全球覆盖海面高格网日值数据。由于数据更新状态的问题,2020-03-07前的数据为非实时产品,2020-03-08~12-31的数据为近实时产品,数据空间分辨率为0.25°×0.25°,时间分辨率为1 d。
利用相关软件读取原始数据,以3倍标准差为判断准则,进行粗差探测和剔除,将数据单位转换为mm。以ETOPO1地形数据为参考标准,对全球海平面变化数据进行陆海分离,可提高非潮汐海洋负荷对地面形变计算的准确性。计算2018-01~12数据的平均值,将其从原始数据中扣除,方便后续球谐分析。
2.2 负荷球谐分析利用海平面变化的等效水高格网,采用负荷球谐分析公式计算负荷球谐系数;然后利用负荷大地高和正常高变化影响计算公式,计算广东地区负荷影响。采用地球潮汐负荷效应与形变监测计算系统ETideLoad辅助相关计算(http://www.zcyphygeodesy.com)。研究发现,非潮汐海洋负荷主要对近海区域影响比较大,距离海洋100 km以内的年变化幅度超过10 mm,如在2020-12-02所在的GPS周,沿海地区非潮汐海洋负荷变化影响非常明显。非潮汐海洋负荷变化对远离海洋的区域影响较小,甚至可以忽略。
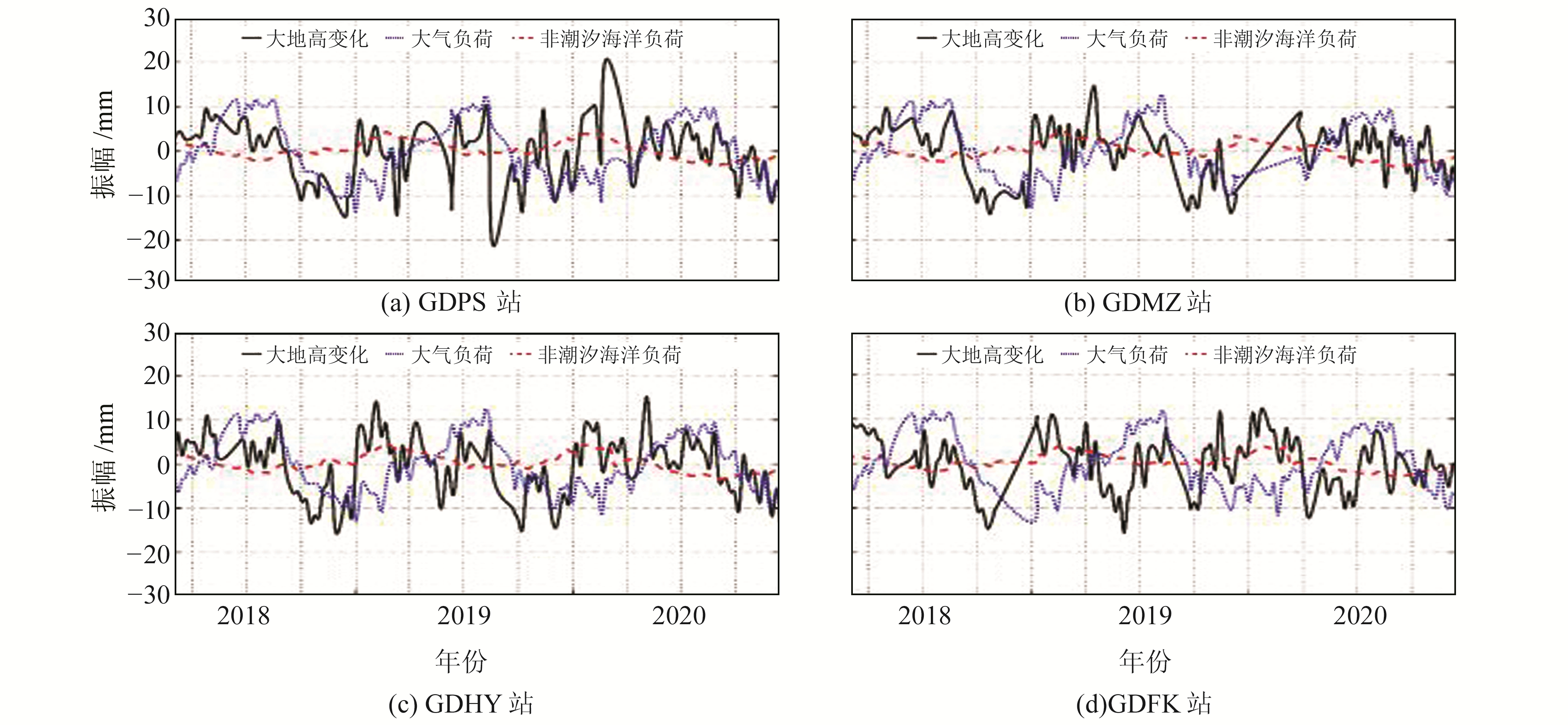
图 1为部分CORS站点处的大地高变化、大气负荷和非潮汐海洋负荷对大地高的影响。大地高变化时序利用解算的日值解经过周平均获得,已扣除线性变化,并未作相应的粗差探测和剔除、数据重构等处理,受多种因素影响,这里仅用于与大气负荷、非潮汐海洋负荷的对比。由图 1可见,大气负荷对大地高的影响相对非潮汐海洋负荷更显著。非潮汐海洋负荷具有明显的年周期性,这与Dam等[9]的研究结果一致。从图 1还可以发现,大气负荷影响和非潮汐海洋负荷影响具有负相关性。
|
图 1 CORS站处的大地高变化、大气负荷和非潮汐海洋负荷对大地高的影响 Fig. 1 Effect on geodetic height of geodetic height variation, atmosphere loading and non-tidal ocean loading at CORS stations |
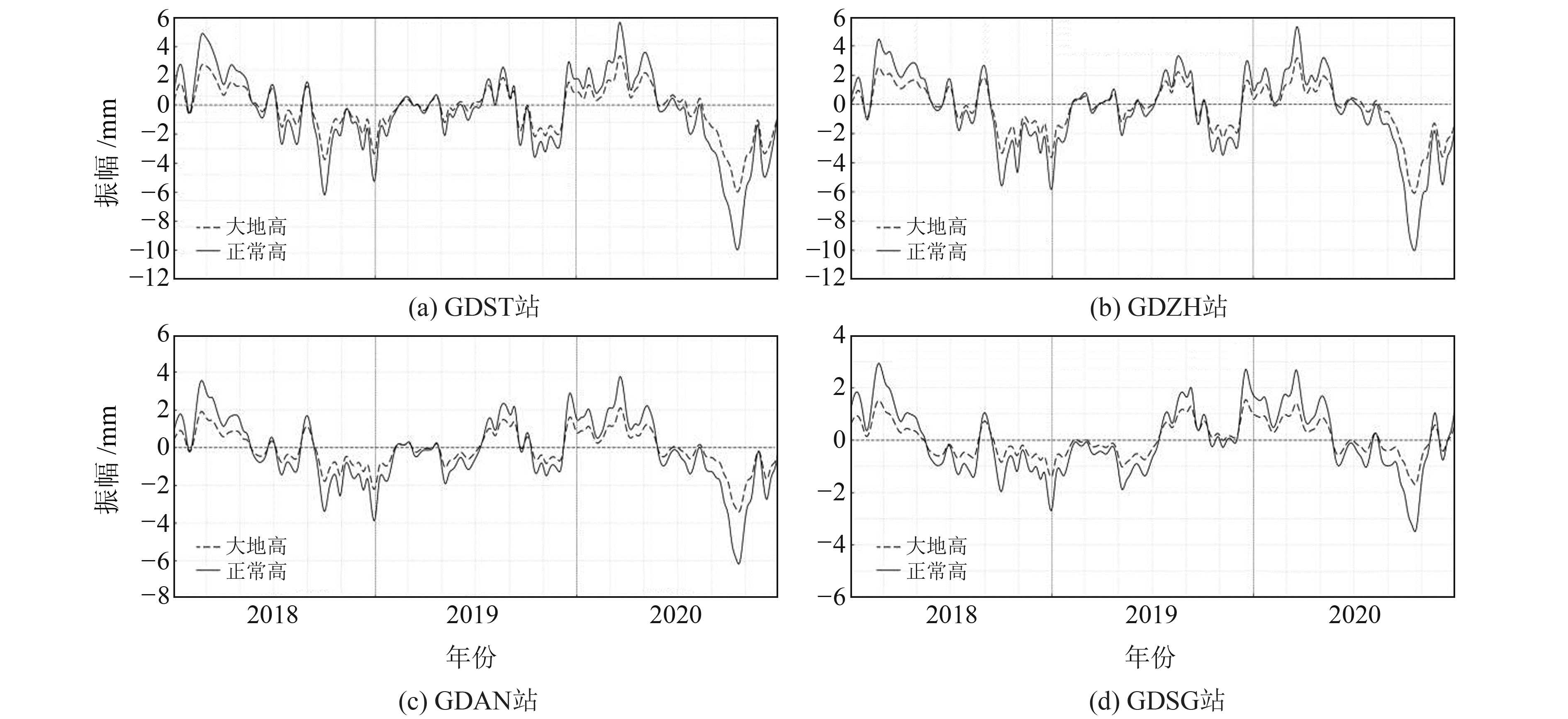
图 2列出了广东地区部分CORS站点非潮汐海洋负荷对大地高和正常高的影响。由图 2可见,汕头GDST站、珠海GDZH站距离海边较近,受影响较大。二者受到的非潮汐海洋负荷影响在沿海具有长波性质,在空间上具有较强的相关性,与国内外研究成果一致[4, 9]。随着与海边距离的增加,非潮汐海洋负荷对大地高和正常高的影响逐渐减小。在距离海洋超过300 km的韶关GDSG站,非潮汐海洋负荷影响在±3 mm内,相比周伯烨等[4]提出的平均影响量级约1.5 mm (距离海岸线200~500 km内)略大。可能因为本文采用的是高精度的实测海面高变化,相比ECCO海底压力模型具有更多高频特征。在远离海洋的内陆地区,非潮汐海洋负荷影响基本可以忽略。
|
图 2 部分CORS站非潮汐海洋负荷对大地高和正常高的影响 Fig. 2 Effect on geodetic height and normal height of non-tidal ocean loading at some CORS stations |
统计广东区域非潮汐海洋负荷变化对大地高、正常高影响的最大值、最小值、平均值和标准差,结果见表 1(单位mm)。
|
|
表 1 非潮汐海洋负荷对大地高和正常高的影响 Tab. 1 Effect on geodetic height and normal height non-tidal ocean loading |
通过以上分析发现,在靠近海洋的地方,非潮汐海洋负荷对高程年变化的影响超过10 mm,与Williams等[3]和周伯烨等[4]的成果在量级上一致,但变化幅度略大。这主要是因为前人采用的是ECCO海底压力模型,该模型需要利用现有的海底地形模型数据,同时在建模中存在一些平滑处理;而本文采用的是由多卫星测高数据综合获取的海面高变化数据,分辨率和精度更高。
4 结语本文采用高精度海平面变化数据,利用球谐分析方法计算广东地区非潮汐海洋负荷对大地高和地面高程变化的影响,并进行相应分析。研究显示,在沿海地区,非潮汐海洋负荷对CORS站点上的形变影响最大超过10 mm,在高精度形变测量分析中需要考虑这种影响;随着离海洋距离的增加,非潮汐海洋负荷的影响逐渐减小。
| [1] |
张捍卫, 郑勇, 赵方泉. 海洋负荷潮汐对测站位移影响的理论研究[J]. 大地测量与地球动力学, 2003, 23(1): 69-73 (Zhang Hanwei, Zheng Yong, Zhao Fangquan. Theoretical Research of Ocean Loading Tide Influence on Station Displacements[J]. Journal of Geodesy and Geodynamics, 2003, 23(1): 69-73)
(  0) 0) |
| [2] |
Zerbini S, Matonti F, Raicich F, et al. Observing and Assessing Nontidal Ocean Loading Using Ocean, Continuous GPS and Gravity Data in the Adriatic Area[J]. Geophysical Research Letters, 2004, 31(23)
(  0) 0) |
| [3] |
Williams S D P, Penna N T. Non-Tidal Ocean Loading Effects on Geodetic GPS Heights[J]. Geophysical Research Letters, 2011, 38(9)
(  0) 0) |
| [4] |
周伯烨, 姜卫平, 李昭. 非潮汐海洋负载效应对近海岸IGS测站坐标时间序列的影响[J]. 大地测量与地球动力学, 2016, 36(11): 1 008-1 013 (Zhou Boye, Jiang Weiping, Li Zhao. Effects of Non-Tidal Ocean Loading on IGS Stations in Coastal Areas[J]. Journal of Geodesy and Geodynamics, 2016, 36(11): 1 008-1 013)
(  0) 0) |
| [5] |
Munekane H, Matsuzaka S. Nontidal Ocean Mass Loading Detected by GPS Observations in the Tropical Pacific Region[J]. Geophysical Research Letters, 2004, 31(8)
(  0) 0) |
| [6] |
陈阜超. GPS非构造垂直形变研究[D]. 武汉: 武汉大学, 2020 (Chen Fuchao. Research on GPS Non-Tectonic Vertical Deformation[D]. Wuhan: Wuhan University, 2020))
(  0) 0) |
| [7] |
马符讯. 欧洲区域测站非线性运动中环境负载的影响研究[D]. 武汉: 武汉大学, 2017 (Ma Fuxun. The Research of the Influence of Environmental Loading on Non-Linear Motion of European GPS Stations[D]. Wuhan: Wuhan University, 2017))
(  0) 0) |
| [8] |
龚国栋, 花向红, 贺小星, 等. GPS坐标时间序列中地表环境负载效应区域特征分析[J]. 大地测量与地球动力学, 2017, 37(9): 961-967 (Gong Guodong, Hua Xianghong, He Xiaoxing, et al. Analysis of Regional Characteristics of Environment Load Effect in GPS Coordinate Time Series[J]. Journal of Geodesy and Geodynamics, 2017, 37(9): 961-967)
(  0) 0) |
| [9] |
Dam T, Collilieux X, Wuite J, et al. Nontidal Ocean Loading: Amplitudes and Potential Effects in GPS Height Time Series[J]. Journal of Geodesy, 2012, 86(11): 1 043-1 057 DOI:10.1007/s00190-012-0564-5
(  0) 0) |
| [10] |
Farrell W E. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics, 1972, 10(3): 761
(  0) 0) |
| [11] |
吴星, 张传定, 赵德军, 等. 广义球谐函数定积分计算方法的改进[J]. 测绘学院学报, 2005, 22(1): 17-20 (Wu Xing, Zhang Chuanding, Zhao Dejun, et al. Improvements on the Computation of Fixed Integral of Generalized Spherical Harmonics[J]. Journal of Institute of Surveying and Mapping, 2005, 22(1): 17-20)
(  0) 0) |
2. South China Sea Marine Survey and Technology Center, SOA, 155 West-Xingang Road, Guangzhou 510300, China;
3. Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road, Beijing 100036, China
 2023, Vol. 43
2023, Vol. 43


