2. 武汉理工大学安全科学与应急管理学院,武汉市珞狮路205号,430070;
3. 湖南省地质院,长沙市万家丽中路106号,410014;
4. 武汉大学测绘学院,武汉市珞喻路129号,430079;
5. 湖南城市学院市政与测绘工程学院,湖南省益阳市迎宾东路518号,413000
地面三维激光扫描技术的可靠性取决于扫描点云数据的质量,而点云数据质量由激光束方向精度决定,激光束方向精度又与测距、测角精度及扫描特征有关[1]。影响点云数据精度的主要因子为系统误差和偶然误差[2]:系统误差主要受仪器本身出厂设置影响,偶然误差主要受目标表面反射特性及外界环境影响[3]。激光扫描仪基于激光束反射原理得到目标点云数据,依据激光能量衰减模型[4]得到激光束反射强度,激光束反射强度主要受目标表面反射特性的影响。
很多学者对点云数据质量进行分析[5-8],为点云数据的应用奠定了基础,但鲜有学者围绕影响点云数据质量的本质性问题进行研究。本文基于激光能量衰减模型,探讨影响激光能量衰减的主要因子,分析影响点云数据质量的主要因素,并基于激光束方向精度构建修正后的测距精度模型,从根本上提高点云数据质量。
1 地面激光扫描激光能量衰减模型假设扫描的点云坐标为(xi, yi, zi),则激光束向量为Pi=[xi yi zi],Pi与表面法向量N之间的夹角为:
| $ \alpha_i=\cos ^{-1}\left(\frac{\boldsymbol{P}_i \cdot \boldsymbol{N}}{\left|\boldsymbol{P}_i\right||\boldsymbol{N}|}\right) $ | (1) |
根据大气激光雷达成像方程,地面激光扫描仪返回的激光能量与发散的激光能量之间的关系为[9]:
| $ P_R(\rho)=P_T \frac{D_R^2 \chi}{4 {\rm{\mathsf{π}}} \rho^4 \beta_t^2} \eta_{\mathrm{sys}} \eta_{\mathrm{atm}} $ | (2) |
式中,PR为接收的激光能量,PT为发射的激光能量,ρ为距离,DR为接收机天线孔径,χ为目标断面,βt为激光波束宽度,ηsys为系统损失,ηatm为大气损失。
根据朗伯体反射特性,目标断面χ为[4]:
| $ \chi={\rm{\mathsf{π}}} \rho^2 \beta_t^2 \gamma \cos \alpha $ | (3) |
式中,γ为反射率,α为入射角。
假设激光在目标表面的散射呈半球形,则接收机天线孔径DR2/4的效应等同于π。将式(3)及DR2/4=π代入式(2),得到适用于地面激光扫描仪的简化激光能量衰减公式:
| $ P_R(\rho)=P_T \frac{\cos \alpha}{\rho^2} {\rm{\mathsf{π}}} \gamma \eta_{\mathrm{sys}} \eta_{\mathrm{atm}} $ | (4) |
利用扫描仪对平面进行扫描,平面点云为p=[xi yi zi]i=1, 2, …, n,采用文献[10]中的正交整体最小二乘法对点云进行平面拟合,得到拟合参数为
| $ \hat{\boldsymbol{e}}_d=\boldsymbol{A} \hat{\boldsymbol{x}} $ | (5) |
式中,
| $ \mathrm{RMSE}_d=\sigma_{\hat{e}_d}=\sqrt{\frac{\hat{\boldsymbol{e}}_d^{\mathrm{T}} {\boldsymbol{w\hat { \boldsymbol { e } }}}_d}{n-m}} $ | (6) |
式中,w为每个点精度的权值,若所有点都是等精度观测,则w为单位矩阵,n为样本总数,m=4为估计参数的个数。
参数估计精度为:
| $ \boldsymbol{Q}_{\hat{x} \hat{x}}=\sigma_{\hat{e}_d}\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{w} \boldsymbol{A}\right)^{-1} $ | (7) |
由式(4)可知,受激光信噪比的影响,扫描的激光点不可能完全在平面上。在入射角为α的情况下,得到平面拟合正交距离与激光束方向扫描距离之间的关系为:
| $ \rho=\frac{d}{\cos \alpha} $ | (8) |
由此得到激光束方向误差为:
| $ \hat{e}_\rho=\frac{\hat{e}_d}{\cos \alpha} $ | (9) |
利用误差传播规律,得到激光束方向标准差为:
| $ \sigma_{\hat{e}_\rho}=\frac{\sigma_{\hat{e}_d}}{\cos \alpha} $ | (10) |
式中,cosα为入射角对激光束方向精度的影响因子:
| $ c_I(\alpha)=\cos \alpha $ | (11) |
由式(4)确定距离对激光束方向精度影响因子:
| $ c_R(\rho)=\frac{\rho_{\max }^2-\rho^2}{\rho_{\max }^2-\rho_{\min }^2} $ | (12) |
式中,ρmax为最远扫描距离,ρmin为最近扫描距离。
同理得反射率对激光束方向精度影响比重:
| $ c_r(\gamma)=\frac{\gamma-\gamma_{\min }}{\gamma_{\max }-\gamma_{\min }} $ | (13) |
式中,γmin为符合朗伯体反射的最小反射率,γmax为符合朗伯体反射的最大反射率。
同时考虑测距、入射角及反射率的影响,由式(11)~(13)得到激光束方向误差与正交误差的关系为:
| $ \begin{gathered} \hat{e}_d=\hat{e}_\rho c_I(\alpha) c_R(\rho) c_r(\gamma), \\ 0 \leqslant c_I(\alpha) 、c_R(\rho) 、c_r(\gamma) \leqslant 1 \end{gathered} $ | (14) |
由式(14)即可得到激光束方向标准差为:
| $ \sigma_{\hat{e}_\rho}=\frac{\sigma_{\hat{e}_d}}{c_I(\alpha) c_R(\rho) c_r(\gamma)} $ | (15) |
在相同条件下,利用Riegl-400扫描仪对不同距离、不同入射角的平板进行扫描,验证距离及入射角对激光束方向精度的影响。实验主要分2个阶段:1)固定材质和入射角,验证距离对激光束方向精度的影响;2)固定材质和距离,验证入射角对激光束噪声的影响。实验方案设计如图 1所示。

|
图 1 不同距离的旋转角度 Fig. 1 Rotation angles at different distances |
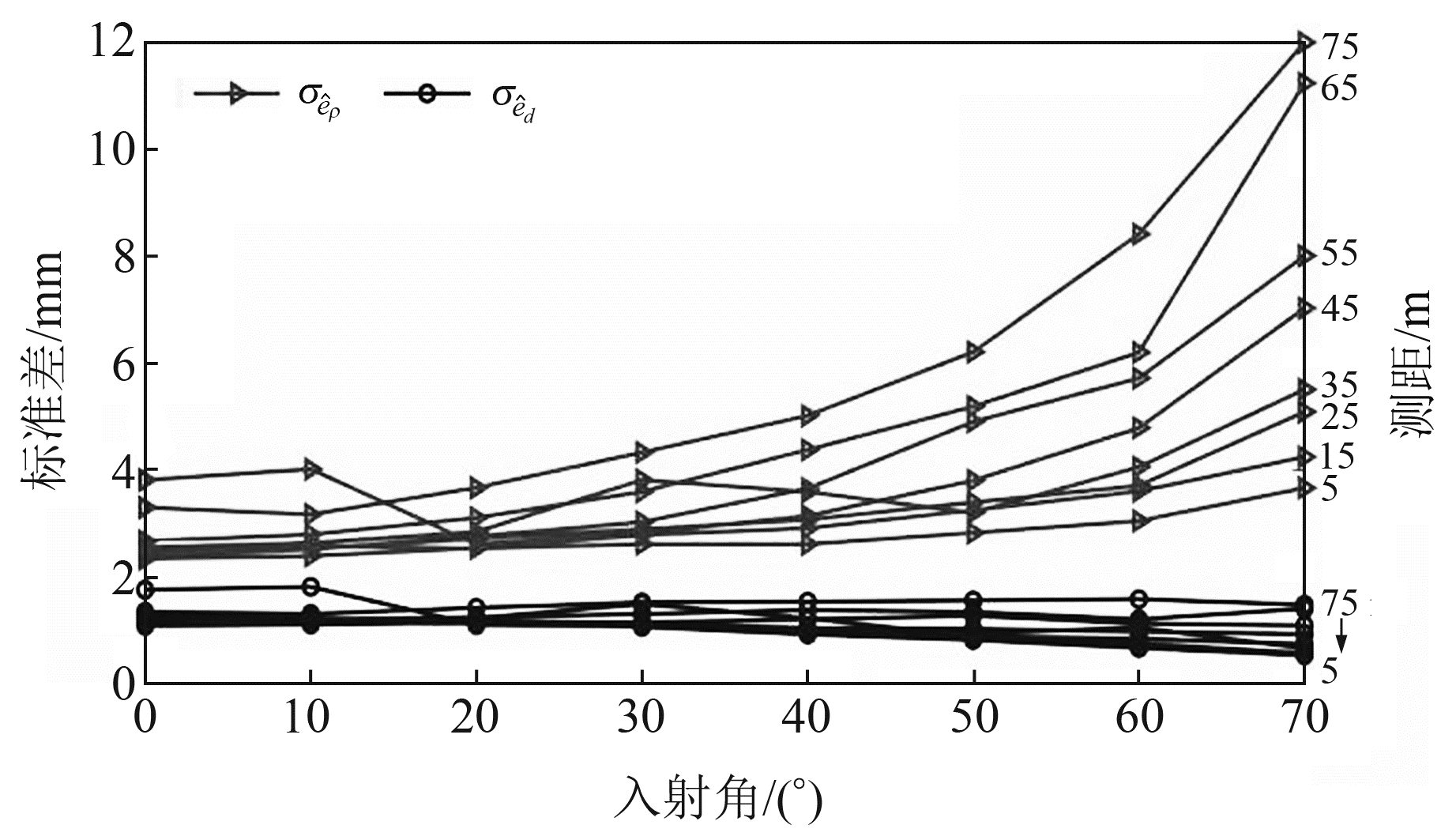
图 2为测距、入射角及反射率对激光束方向精度的影响。由图可见,考虑测距及入射角的激光束方向精度明显高于不考虑任何影响的平面拟合正交残差的标准差。根据入射角和测距对激光束方向精度的影响因子模型可知,相较于测距,入射角对激光束方向精度的影响较大,100 m范围以内的影响尤其明显。
|
图 2 测距、入射角及反射率对激光束方向精度的影响 Fig. 2 Influence of ranging, incident angle and reflectance on laser beam accuracy |
假设由激光能量衰减模型推导出的激光束方向精度为σext,由测距、测角、光斑推导的激光束方向精度为σint。利用测距、测角精度解算2种模型推导的激光束方向精度,如图 3所示。

|
图 3 2种模型的激光束方向精度 Fig. 3 Laser beam direction accuracy of two models |
由图 3(a)可知,当入射角接近0°时,2种模型的激光束方向精度基本相同,说明该条件下的激光束方向精度较为真实可靠;由图 3(b)可知,随着测距的增加,2种模型的激光束方向精度呈相似的递增趋势。
5 激光束方向精度反演测距精度根据式(15),利用激光能量衰减模型反演出不同入射角下的测距精度,如图 4所示。

|
图 4 测距精度 Fig. 4 Ranging accuracy |
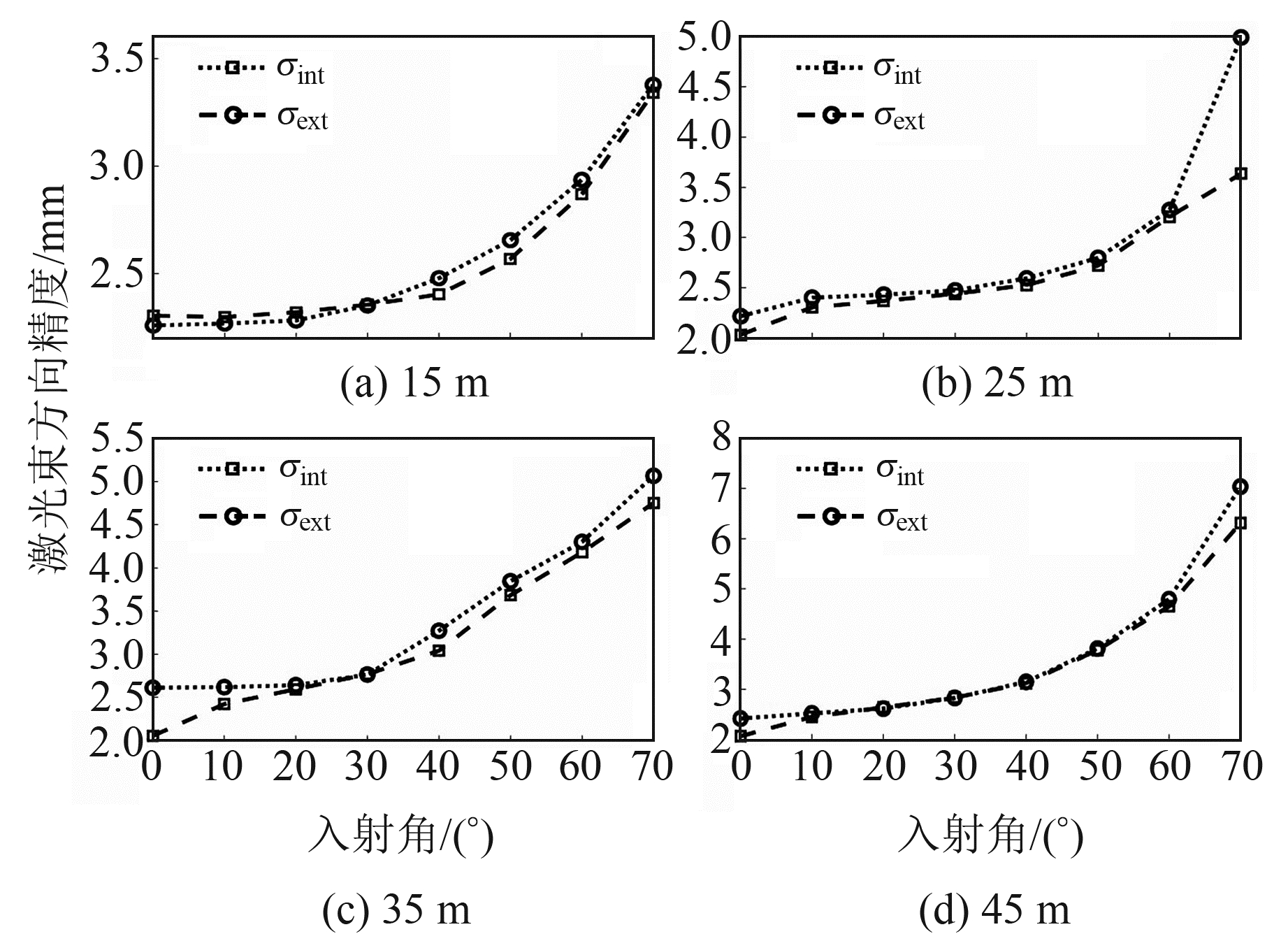
由图 4可见,入射角对测距精度的影响随距离的增加而增大。根据反演后的测距精度,利用点位误差椭球重新计算激光束方向精度σint,并将该精度与利用激光能量衰减模型推导的激光束方向精度σext进行对比分析,结果如图 5所示。
|
图 5 测距精度反演后的激光束方向精度 Fig. 5 Laser beam direction accuracy after ranging accuracy inversion |
由图 5可见,随着入射角的增大,2种模型推导出的激光束方向精度基本相同。由此可知,利用激光能量衰减模型可以实现不同入射角下测距精度的模拟。
6 结语针对三维激光扫描仪激光束方向精度,结合平面拟合正交距离与激光束方向距离的直接关系模型,研究激光束方向精度影响系数,利用平面拟合误差分析不同扫描距离及入射角对平面点云数据质量的影响。结果表明,激光扫描仪测距由15 m逐步增加到45 m时,激光束方向精度变化较为平缓,验证了基于激光束方向精度反演地面激光扫描测距精度的可行性。
| [1] |
杨蒙蒙, 万幼川, 徐景中. 激光扫描仪四棱塔镜误差分析及定位精度研究[J]. 中国激光, 2015, 42(9): 324-331 (Yang Mengmeng, Wan Youchuan, Xu Jingzhong. Research of Error Analysis and Positioning Accuracy with Four-Prism of Laser Scanning[J]. Chinese Journal of Lasers, 2015, 42(9): 324-331)
(  0) 0) |
| [2] |
郑德华, 沈云中, 刘春. 三维激光扫描仪及其测量误差影响因素分析[J]. 测绘工程, 2005, 14(2): 32-34 (Zheng Dehua, Shen Yunzhong, Liu Chun. 3D Laser Scanner and Its Effect Factor Analysis of Surveying Error[J]. Engineering of Surveying and Mapping, 2005, 14(2): 32-34)
(  0) 0) |
| [3] |
严良平, 潘月梁, 徐琼, 等. 材料表面涂层对三维激光扫描数据精度的影响分析[J]. 测绘工程, 2022, 31(5): 9-15 (Yan Liangping, Pan Yueliang, Xu Qiong, et al. Impact Analysis of Material Surface Coating on the Precision of 3D Laser Scanning Data[J]. Engineering of Surveying and Mapping, 2022, 31(5): 9-15)
(  0) 0) |
| [4] |
Soudarissanane S, Lindenbergh R, Menenti M, et al. Scanning Geometry: Influencing Factor on the Quality of Terrestrial Laser Scanning Points[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(4): 389-399 DOI:10.1016/j.isprsjprs.2011.01.005
(  0) 0) |
| [5] |
李佳龙, 郑德华, 何丽, 等. 目标颜色和入射角对Trimble GX扫描点云精度的影响[J]. 测绘工程, 2012, 21(5): 75-79 (Li Jialong, Zheng Dehua, He Li, et al. The Effects of Known Color and Incidence Angle on the Accuracy of Trimble GX 3D Scanning Point Cloud[J]. Engineering of Surveying and Mapping, 2012, 21(5): 75-79)
(  0) 0) |
| [6] |
Bolkas D, Martinez A. Effect of Target Color and Scanning Geometry on Terrestrial LiDAR Point-Cloud Noise and Plane Fitting[J]. Journal of Applied Geodesy, 2018, 12(1): 109-127 DOI:10.1515/jag-2017-0034
(  0) 0) |
| [7] |
孙德勇, 许烨璋, 段文义, 等. 地面三维激光扫描点云平面拟合精度测试与分析[J]. 勘察科学技术, 2021(1): 23-27 (Sun Deyong, Xu Yezhang, Duan Wenyi, et al. Accuracy Test and Analysis for Plane Fitting Precision of Point Cloud from Ground 3D Laser Scanning[J]. Site Investigation Science and Technology, 2021(1): 23-27)
(  0) 0) |
| [8] |
Chen X J, Zhang G, Hua X H, et al. An Average Error-Ellipsoid Model for Evaluating TLS Point-Cloud Accuracy[J]. The Photogrammetric Record, 2016, 31(153): 71-87
(  0) 0) |
| [9] |
Rees W G. Physical Principles of Remote Sensing: Electromagnetic Waves in Free Space[M]. Cambridge: Cambridge University Press, 2012
(  0) 0) |
| [10] |
张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004 (Zhang Xianda. Matrix Analysis and Application[M]. Beijing: Tsinghua University Press, 2004)
(  0) 0) |
2. School of Safety Sciences and Emergency Management, Wuhan University of Technology, 205 Luoshi Road, Wuhan 430070, China;
3. Geological Bureau of Hunan Province, 106 Mid-Wanjiali Road, Changsha 410014, China;
4. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China;
5. School of Municipal and Geomatics Engineering, Hunan City University, 518 East-Yingbin Road, Yiyang 413000, China
 2023, Vol. 43
2023, Vol. 43


