由Bayes估计原理可知，当先验信息和观测信息均可靠时，参数最小二乘估计满足无偏、一致、有效性^[1-2]。但当先验信息不可靠时，先验信息和观测信息对参数解的贡献不同。这时需要给先验信息赋予一个权值以平衡观测信息与先验信息的权比，从而控制先验信息对参数解的影响^[3]。许多学者研究了先验信息的权值问题，如Durbin^[4]和Theil等^[5-6]提出混合估计方法，Schaffrin等^[7]在混合估计的基础上提出加权混合估计。这些算法大多注重于计算效率和估计的优良性，没有提供先验信息权值的计算方法，不能直接用于大地测量数据处理。平衡损失函数综合考虑模型拟合优度与参数估计的精度，建立了一个新的参数估计准则^{[2, 8]}。在统计决策上，它是使均方误差达到最小的估计^[8]。由于现有的算法无法计算先验信息权值，平衡估计方法在测绘工程中的应用较少。本文基于Bayes估计原理，在平衡估计准则的基础上，研究观测信息可靠时先验信息对平差结果的影响，建立先验信息的判别统计量，给出一个自适应计算平衡因子的方法，控制不准确的先验信息对参数解的影响。

1 参数的Bayes估计

一般平差模型可写为：

$ \boldsymbol{L}=\boldsymbol{A} \boldsymbol{X}+\boldsymbol{e} $

(1)

式中，A为m×n维系数矩阵，rank(A) < n；L为m维观测向量；e为m维误差向量，其分布函数为N(0, Σ)，E(e)=0，cov(e)=Σ=σ²P^－1；X=(x₀, x₂, …, x_n)^T为n维未知参数向量。若假设X的先验分布为正态分布，即f(X)=N(X₀, Σ_X)，则：

$ E(\boldsymbol{X})=\boldsymbol{X}_0, \operatorname{cov}(\boldsymbol{X})=\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_X=\boldsymbol{S}^{-1} $

(2)

式中，X₀是已知向量；Σ_X为已知正定矩阵。观测向量L的条件分布f(L|X)=N(AX, Σ)，可得到参数向量X的验后分布为^[9]：

$ \begin{array}{*{20}{c}} & f(\boldsymbol{X} \mid \boldsymbol{L}) \propto \exp \left\{-\frac{1}{2 \sigma^2}\left[\left(\boldsymbol{X}-\boldsymbol{X}_0\right)^{\mathrm{T}} \boldsymbol{S}\left(\boldsymbol{X}-\boldsymbol{X}_0\right)+\right.\right. \\ & \left.\left.(\boldsymbol{L}-\boldsymbol{A} \boldsymbol{X})^{\mathrm{T}} \boldsymbol{P}(\boldsymbol{L}-\boldsymbol{A} \boldsymbol{X})\right]\right\} \\ \end{array} $

(3)

式中，∝表示成正比例关系。由Bayes估计的准则^[10]，f(X|L)=max，因此有：

$ \begin{gathered} (\boldsymbol{L}-\boldsymbol{A} \boldsymbol{X})^{\mathrm{T}} \boldsymbol{P}(\boldsymbol{L}-\boldsymbol{A} \boldsymbol{X})+ \\ \left(\boldsymbol{X}-\boldsymbol{X}_0\right)^{\mathrm{T}} \boldsymbol{S}\left(\boldsymbol{X}-\boldsymbol{X}_0\right)=\min \end{gathered} $

(4)

由式(4)对X求极值，由矩阵的微分法得：

$ \left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{A}+\boldsymbol{S}\right) \boldsymbol{X}=\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{L}+\boldsymbol{S} \boldsymbol{X}_0 $

(5)

设由Bayes估计准则得到的参数估计(极大后验估计)为$\hat{\boldsymbol{X}}_B$，则：

$ \hat{\boldsymbol{X}}_B=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{A}+\boldsymbol{S}\right)^{-1}\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{L}+\boldsymbol{S} \boldsymbol{X}_0\right) $

(6)

可以看出，X的Bayes线性无偏估计是先验信息X₀和观测信息L的一个线性组合。当观测信息的先验信息和观测信息可靠(观测误差服从正态分布)时，参数极大验后估计是一个线性无偏最小方差估计^[3]。

2 平衡准则下的参数估计

为了平衡观测信息与先验信息的权比，控制不准确的先验信息对参数解的影响，在式(4)的基础上给先验信息赋予一个权值：

$ \begin{gathered} (\boldsymbol{L}-\boldsymbol{A} \boldsymbol{X})^{\mathrm{T}} \boldsymbol{P}(\boldsymbol{L}-\boldsymbol{A} \boldsymbol{X})+ \\ \alpha\left(\boldsymbol{X}-\boldsymbol{X}_0\right)^{\mathrm{T}} \boldsymbol{S}\left(\boldsymbol{X}-\boldsymbol{X}_0\right)=\min \end{gathered} $

(7)

对参数向量X求极值：

$ -\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P}(\boldsymbol{L}-\boldsymbol{A} \boldsymbol{X})+\alpha \boldsymbol{S}\left(\boldsymbol{X}-\boldsymbol{X}_0\right)=0 $

(8)

设由平衡准则式(7)得到的平衡估计为$\hat{\boldsymbol{X}}_P$，则:

$ \hat{\boldsymbol{X}}_P=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{A}+\alpha \boldsymbol{S}\right)^{-1}\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{L}+\alpha \boldsymbol{S} \boldsymbol{X}_0\right) $

(9)

从平衡最小二乘解$\hat{\boldsymbol{X}}_P$的表达式可以看出，利用平衡因子α可以平衡观测信息和先验信息对参数估计的影响。由于$\hat{\boldsymbol{X}}_P$与L不相关，利用协方差矩阵传播定律可以得出$\hat{\boldsymbol{X}}_P$的协方差矩阵为：

$ \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\hat{X}_P}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{A}+\alpha \boldsymbol{S}\right)^{-1} $

(10)

利用平衡因子α可以控制先验信息异常对参数估值的影响。文献[8]证明了$\hat{\boldsymbol{X}}_P$优于最小二乘估计$\hat{\boldsymbol{X}}_{\rm{LS}}$的充要条件是α>1，但在实际工程中如何确定α的值是一个非常复杂的问题，现有的文献还没有关于α的计算方法。本文将对此进行研究。

3 平衡因子的计算

由于残差V_X=$\hat{\boldsymbol{X}}_{\rm{LS}}$－X₀可以反映出观测信息与先验信息的误差量级，故利用其来设计一个计算平衡因子的方法。在测绘工程中，一般假设观测信息是可靠的，如果观测信息不可靠(如存在粗差)，可以采用抗差估计方法计算等价权。如果观测信息可靠，先验信息也可靠，则由最小二乘得到的参数解与先验信息X₀之差应该很小；反之，若观测信息可靠，且残差V_X很大，则表明先验信息不准确。如此，可以依据残差V_X构造判别统计量：

$ \Delta \widetilde{X}=\left\|\hat{\boldsymbol{X}}_{\mathrm{LS}}-\boldsymbol{X}_0\right\| / \sqrt{\operatorname{tr}\left(\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{X_0}\right)} $

(11)

式中，tr表示迹，$\hat{\boldsymbol{X}}_{\rm{LS}}$－X₀=(Δx₁, Δx₂, …, Δx_m)^T。

$ \begin{gathered} \left\|\hat{\boldsymbol{X}}_{\mathrm{LS}}-\boldsymbol{X}_0\right\|= \\ \left(\Delta x_1^2+\Delta x_2^2+\cdots+\Delta x_m^2\right)^{1 / 2} \end{gathered} $

(12)

下面是根据统计量构造的一个两段函数平衡因子，其原理类似于Huber函数^[11]：

$ \alpha=\left\{\begin{array}{l} 1, |\Delta \widetilde{X}| \leqslant c \\ \frac{c}{|\Delta \widetilde{X}|}, |\Delta \widetilde{X}|>c \end{array}\right. $

(13)

式中，c为常数，取值在1.0~2.5之间^[11]，本文取1.2。显然，$|\Delta \widetilde{X}|$越大，α越小，α满足0≤α≤1。

4 模拟算例

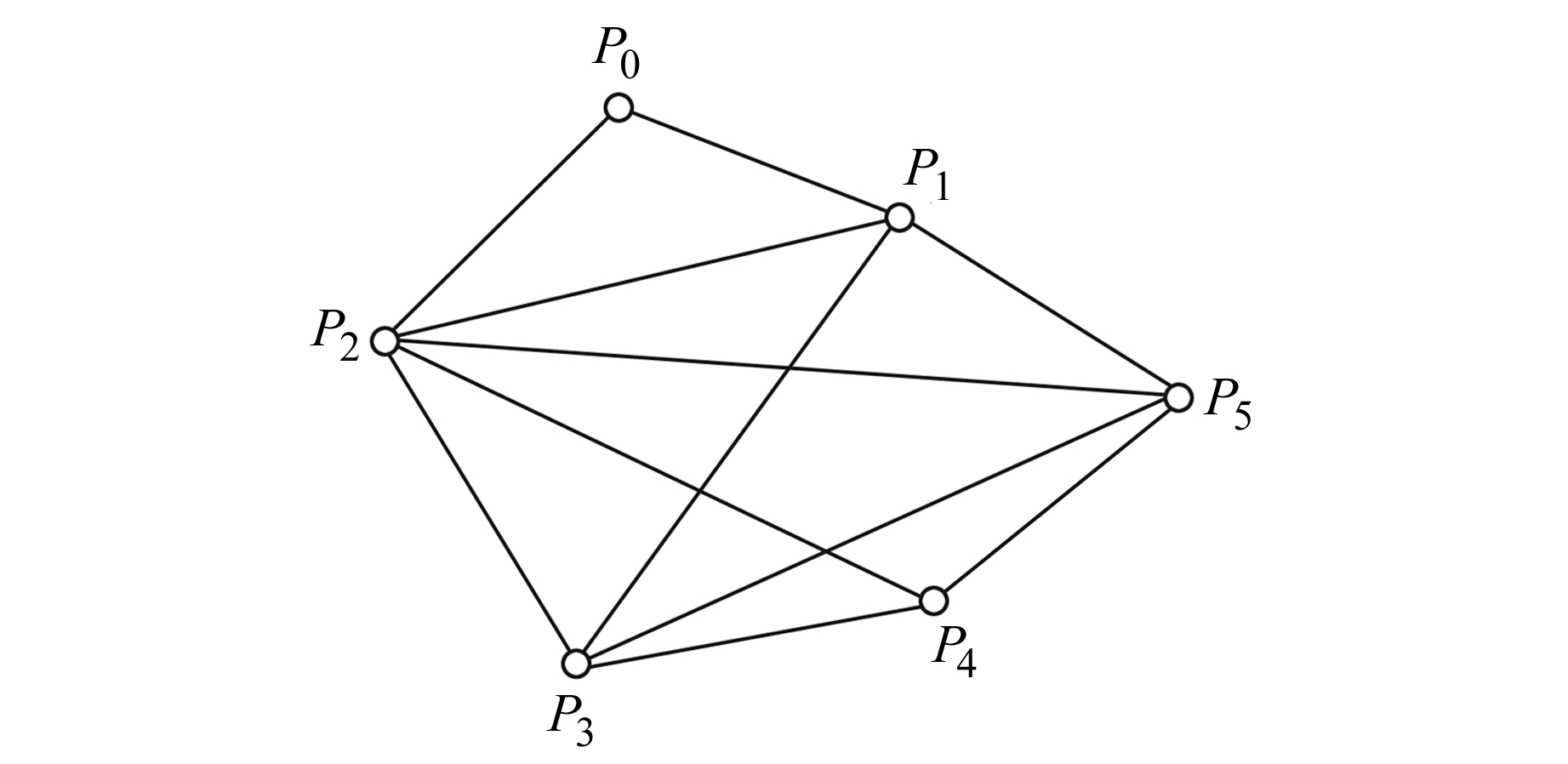
为了验证平衡估计在参数解算中的效果，设计如下算例：设有一测边网(图 1)，P₀为起算点，P₁、P₂、P₃、P₄、P₅的真实坐标已知(表 1)，边长的观测值是利用真实坐标与随机误差计算得到的，误差范围为(-0.05 m, 0.05 m)，观测边长视为同精度(表 2)。相对于近似坐标的改正数构成的未知向量为X =[x₁, y₁, x₂, y₂, x₃, y₃, x₄, y₄, x₅, y₅]^T。

对观测方程进行线性化可以得到相应平差模型L = AX + e，其中，A和L为别为：

$ \begin{gathered} \boldsymbol{L}=(-0.158\;9, 0.436\;8, -2.535\;2, -1.430\;0, -0.0411, -0.774\;4, \\ \quad 2.870\;3, 0.058\;1, -0.637\;9, -0.360\;0, -1.774\;4, -1.154\;8)^{\mathrm{T}} \end{gathered} $

$ \mathit{\boldsymbol{A = }}\left[ {\begin{array}{*{20}{c}} {0.945\;4}&{ - 0.325\;8}&0&0&0&0&0&0&0&0\\ 0&0&{0.999\;4}&{ - 0.035\;7}&0&0&0&0&0&0\\ {0.836\;0}&{0.505\;2}&{ - 0.863\;0}&{ - 0.505\;2}&0&0&0&0&0&0\\ {0.566\;6}&{0.824\;0}&0&0&{ - 0.566\;6}&{ - 0.824\;0}&0&0&0&0\\ {0.690\;8}&{0.723\;0}&0&0&0&0&{ - 0.690\;8}&{ - 0.723\;0}&0&0\\ { - 0.499\;4}&{0.866\;4}&0&0&0&0&0&0&{0.499\;4}&{ - 0.866\;4}\\ 0&0&{ - 0.791\;5}&{0.611\;2}&{0.791\;5}&{ - 0.611\;2}&0&0&0&0\\ 0&0&{ - 0.977\;3}&{ - 0.211\;7}&0&0&{0.977\;3}&{0.211\;7}&0&0\\ 0&0&{ - 0.994\;5}&{0.104\;4}&0&0&0&0&{0.994\;5}&{ - 0.104\;4}\\ 0&0&0&0&{ - 0.365\;2}&{ - 0.930\;9}&{0.365\;2}&{0.930\;9}&0&0\\ 0&0&0&0&{ - 0.989\;3}&{ - 0.145\;6}&0&0&{0.989\;3}&{0.145\;6}\\ 0&0&0&0&0&0&{ - 0.954\;9}&{0.296\;9}&{0.954\;9}&{ - 0.296\;9} \end{array}} \right] $

为验证平衡因子的有效性，假设前期观测得到的参数估计值有2个：一个是$\hat{\boldsymbol{X}}_0$，其协方差阵为$\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\hat{X}_0}$=0.2 I；另一个是X₀，其协方差阵为Σ_X0=2 I。设计如下参数估计方法来比较和说明算法的效率。

1) 经典最小二乘估计：$\hat{\boldsymbol{X}}_{\rm{LS}}$=(A^TPA)^－1A^TPL。

2) 对应先验信息$\hat{\boldsymbol{X}}_{\rm{0}}$的最大后验估计：$\hat{\boldsymbol{X}}_{{B}}$=(A^TPA + S)^－1(A^TPL + S$\hat{\boldsymbol{X}}_{\rm{0}}$)。

3) 对应先验信息$\hat{\boldsymbol{X}}_{\rm{0}}$的带有平衡因子的平衡估计：$\hat{\boldsymbol{X}}_{{P}}$=(A^TPA + αS)^－1(A^TPL + αS$\hat{\boldsymbol{X}}_{\rm{0}}$)。

4) 对应先验信息X₀的最大后验估计：$\hat{\boldsymbol{X}}_{B_1}$=(A^TPA + S₁)^－1(A^TPL + S₁$\hat{\boldsymbol{X}}_{\rm{0}}$)。

5) 对应先验信息X₀的带有平衡因子的平衡估计：$\hat{\boldsymbol{X}}_{P_1}$=(A^TPA + αS₁)^－1(A^TPL + αS₁$\hat{\boldsymbol{X}}_{\rm{0}}$)。

计算结果见表 3，算例分析与说明如下。

1) $\hat{\boldsymbol{X}}_{P}$和$\hat{\boldsymbol{X}}_{P_1}$中的α由式(13)计算得到，算法中c₀=1.2，计算结果分别为α₁=0.919 9, α₂=0.587 9。

2) 表 3中的m(X)表示如下的均方误差：

$ m(\boldsymbol{X})=\left(\hat{\boldsymbol{X}}-\boldsymbol{X}_{\text {real }}\right)^{\mathrm{T}}\left(\hat{\boldsymbol{X}}-\boldsymbol{X}_{\text {real }}\right) $

式中，X_real为真值。

3) 由于系数矩阵A病态，其法矩阵的条件数为2.916 7×10¹⁷，最小二乘估计的结果$\hat{\boldsymbol{X}}_{{\rm{LS}}}$不可靠，其均方误差偏大。

4) 准确的先验信息可以改善模型的病态性；不准确的先验信息若不进行平衡因子的调节，不能改善模型的病态性，见$\hat{\boldsymbol{X}}_{B}$和$\hat{\boldsymbol{X}}_{B_1}$。

5) 利用平衡估计准则可以很好地改善参数估计的性能，提高参数估计的准确性。α₁=0.919 9说明当先验信息准确度高时，平衡因子给予观测信息的权大；α₂=0.587 9说明当先验信息准确度低时，平衡因子给予观测信息更小的权，验证了本文方法具有按照先验信息自适应调节平衡的功能。

6) 从$\hat{\boldsymbol{X}}_{B}$和$\hat{\boldsymbol{X}}_{B_1}$的均方误差可以看出，Bayes线性无偏估计虽然可以利用先验信息，但不能控制先验信息不准确的影响。

5 结语

利用先验信息来进行参数估计，需要控制先验信息异常对参数估值的影响。合理的平衡因子可以平衡平差模型信息与先验信息的权比，控制不准确的先验信息对参数解的影响。本文给出的统计量V_X=$\hat{\boldsymbol{X}}_{{\rm{LS}}}$－X₀可以反映出观测信息与先验信息的误差量级，若观测信息和先验信息可靠，则由最小二乘得到的参数解与先验信息X₀之差应该很小；反之，若观测信息可靠，且残差V_X很大，则表明先验信息不准确，本文依此给出一种平衡因子的计算方法。然而，本文方法是假定观测信息可靠的前提下得到的，如果观测信息不可靠(如存在粗差)，还需要利用抗差估计理论进行等价权的计算。