2. 海军航空大学,山东省烟台市,264001;
3. 山东南山铝业股份有限公司,山东省烟台市南山南路6号,265706
SINS/GNSS组合导航时,若滤波过程中出现量测噪声异常,则会导致滤波精度下降甚至发散[1]。可以使用带有量测噪声估计器的自适应滤波解决此问题[2-5]。如邓传远[2]、曾庆化等[3]对基于标准Sage-Husa的组合导航自适应卡尔曼滤波进行研究,提高了组合导航的精度。但将Sage-Husa自适应卡尔曼滤波应用于组合导航系统中存在2个问题[4]:1)由于组合导航系统阶次比较高,往往存在滤波发散的情况;2)在状态及观测误差不稳定时,组合导航系统也会存在滤波发散现象。为此,本文提出一种改进的Sage-Husa自适应滤波算法。
1 组合导航系统模型导航坐标系取东北天地理坐标系,GNSS/SINS组合导航系统的状态方程表示为[6]:
| $ \boldsymbol{X}_k=\mathit{\boldsymbol{ \boldsymbol{\varPhi}}}_{k, k-1} \boldsymbol{X}_{k-1}+{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k - 1}}\boldsymbol{W}_{k-1} $ | (1) |
式中,Xk=[φE φN φU δvE δvN δvU δλ δL δh εx εy εz ▽x ▽y ▽z]T为k时刻的状态向量,其中,φE、φN、φU为数字平台角误差,δvE、δvN、δvU为速度误差,δλ、δL、δh为经度误差、纬度误差和高度误差,εx、εy、εz为三轴陀螺误差的一阶Markov过程,▽x、▽y、▽z为三轴加速度计误差的一阶Markov过程;Φk, k-1为状态一步转移矩阵;Γk-1为系统噪声矩阵;Wk-1为系统噪声。
GNSS/SINS组合导航系统的量测方程为:
| $ \boldsymbol{Z}_k=\boldsymbol{H}_k \boldsymbol{X}_k+\boldsymbol{V}_k $ | (2) |
式中,观测向量Zk取GNSS和SINS三维位置、三维速度的差值;观测噪声Vk近似为白噪声。
基于标准Sage-Husa自适应滤波的GNSS/SINS组合导航的常规卡尔曼滤波算法为[4]:
| $ \hat{\boldsymbol{X}}_{k \mid k-1}=\mathit{\boldsymbol{ \boldsymbol{\varPhi}}}_{k, k-1} \hat{\boldsymbol{X}}_{k-1 \mid k-1} $ | (3) |
| $ \boldsymbol{P}_{k \mid k-1}=\mathit{\boldsymbol{ \boldsymbol{\varPhi}}}_{k, k-1} \boldsymbol{P}_{k-1 \mid k-1} \mathit{\boldsymbol{ \boldsymbol{\varPhi}}}_{k, k-1}^{\mathrm{T}}+\mathit{\boldsymbol{ \boldsymbol{\varGamma}}}_{k-1} \boldsymbol{Q}_{k-1} \mathit{\boldsymbol{ \boldsymbol{\varGamma}}}_{k-1}^{\mathrm{T}} $ | (4) |
| $ \boldsymbol{K}_k=\boldsymbol{P}_{k \mid k-1} \boldsymbol{H}_k^{\mathrm{T}}\left(\boldsymbol{H}_k \boldsymbol{P}_{k \mid k-1} \boldsymbol{H}_k^{\mathrm{T}}+\hat{\boldsymbol{R}}_k\right)^{-1} $ | (5) |
| $ \boldsymbol{P}_{k \mid k}=\left[\boldsymbol{I}-\boldsymbol{K}_k \boldsymbol{H}_k\right] \boldsymbol{P}_{k \mid k-1} $ | (6) |
| $ \hat{\boldsymbol{X}}_{k \mid k}=\hat{\boldsymbol{X}}_{k \mid k-1}+\boldsymbol{K}_k\left(\boldsymbol{Z}_k-\boldsymbol{H}_k \hat{\boldsymbol{X}}_{k \mid k-1}\right) $ | (7) |
式中,各项参数的详细定义可以参考文献[6];式(5)中
式(3)为状态向量的预测值,则新息向量为:
| $ \boldsymbol{\varepsilon}_k=\boldsymbol{Z}_k-\boldsymbol{H}_k \hat{\boldsymbol{X}}_{k \mid k-1} $ | (8) |
基于标准Sage-Husa的估计方法为[5]:
| $ \hat{\boldsymbol{R}}_k=\left(1-d_k\right) \hat{\boldsymbol{R}}_{k-1}+d_k\left(\boldsymbol{\varepsilon}_k \boldsymbol{\varepsilon}_k^{\mathrm{T}}-\boldsymbol{H}_k \boldsymbol{P}_{k, k-1} \boldsymbol{H}_k^{\mathrm{T}}\right) $ | (9) |
| $ d_k=\frac{1-b}{1-b^k}, k=1, 2, \cdots $ | (10) |
式中,b为遗忘因子(0<b<1),b越小,对新的量测噪声变化的适应能力越强,估计结果跳变越剧烈;反之,对新的量测噪声变化的适应能力越弱。
在组合导航系统的最优卡尔曼滤波方程中,要求量测噪声的方差矩阵
在对GNSS/SINS组合导航系统运用式(3)~(7)的最优线性卡尔曼滤波时,目前常采用补偿反馈校正法,即滤波器工作时间内任何时刻均需对元件施加校正量。采用补偿反馈校正法时,考虑到工程实现,式(3)变为[1]:
| $ \hat{\boldsymbol{X}}_{k \mid k-1}=\bf{0} $ | (11) |
此时,式(8)变为:
| $ \boldsymbol{\varepsilon}_k=\boldsymbol{Z}_k=\boldsymbol{H}_k \boldsymbol{X}_k+\boldsymbol{V}_k $ | (12) |
则有:
| $ E\left[\boldsymbol{\varepsilon}_k \boldsymbol{\varepsilon}_k^{\mathrm{T}}\right]=E\left[\boldsymbol{Z}_k \boldsymbol{Z}_k^{\mathrm{T}}\right]=E\left[\boldsymbol{V}_k \boldsymbol{V}_k^{\mathrm{T}}\right]=\boldsymbol{R}_k $ | (13) |
式中,E[εkεkT]表示新息向量的方差,可取一段时间内的均值代替。用渐消记忆加权对Rk进行估计,加权系数满足[5]:
| $ \left\{\begin{array}{l} \sum\limits_{i=1}^k \beta_i=1 \\ \beta_{i-1}=b \beta_i \end{array}, \quad i=1, 2, \cdots, k\right. $ | (14) |
根据式(14)构建加权系数:
| $ \left\{\begin{array}{l} \beta_i=d_k b^{k-i} \\ d_k=\frac{1-b}{1-b^k}, \quad i=1, 2, \cdots, k \end{array}\right. $ | (15) |
对Rk进行估计:
| $ \begin{gathered} \hat{\boldsymbol{R}}_k=\sum\limits_{i=1}^k \beta_i \boldsymbol{Z}_i \boldsymbol{Z}_i^{\mathrm{T}}=\sum\limits_{i=1}^k d_k b^{k-i} \boldsymbol{Z}_i \boldsymbol{Z}_i^{\mathrm{T}}= \\ \sum\limits_{i=1}^{k-1} d_k b^{k-i} \boldsymbol{Z}_i \boldsymbol{Z}_i^{\mathrm{T}}+d_k \boldsymbol{Z}_k \boldsymbol{Z}_k^{\mathrm{T}}= \\ \frac{d_k b}{d_{k-1}} \sum\limits_{i=1}^{k-1} d_{k-1} b^{k-1-i} \boldsymbol{Z}_i \boldsymbol{Z}_i^{\mathrm{T}}+d_k \boldsymbol{Z}_k \boldsymbol{Z}_k^{\mathrm{T}}= \\ \left(1-d_k\right) \hat{\boldsymbol{R}}_{k-1}+d_k \boldsymbol{Z}_k \boldsymbol{Z}_k^{\mathrm{T}} \end{gathered} $ | (16) |
为了保证
| $ \hat{\boldsymbol{R}}_k=\left(1-d_k\right) \hat{\boldsymbol{R}}_{k-1}+d_k \operatorname{diag}\left[\operatorname{diag}\left(\boldsymbol{Z}_k \boldsymbol{Z}_k^{\mathrm{T}}\right)\right] $ | (17) |
式中,diag(·)是以某个向量为主对角线元素产生对角矩阵的函数,或以向量的形式返回一个矩阵上对角线元素的函数。
3 仿真结果及分析 3.1 仿真条件仿真参数设置如下:初始纬度、经度、高度分别为29°N、118°E、50 m,水平姿态角为0°,方向正北。设定陀螺常值漂移为3°/h,随机游走为0.3°/
根据上述设定,在正常情况下,GNSS量测噪声的RMS矩阵可以表示为:
| $ \begin{gathered} \boldsymbol{r}_{\text {root }}=\operatorname{sqrtm}(\boldsymbol{R})= \\ \operatorname{diag}\left(\left[\begin{array}{llllll} 8 & 8 & 8 & 0.2 & 0.2 & 0.2 \end{array}\right]\right) \end{gathered} $ |
式中,sqrtm(R)为对R中每个元素取开平方。
设置包括变速、爬升、转弯、平飞等机动过程的飞行航迹,飞行时间为3 600 s。飞行过程中,在不同时间段内设定GNSS量测噪声RMS稳定、发生突变与缓变3种情况,具体变化为:
| $ \boldsymbol{r}_{\text {real }}=\left\{\begin{array}{l} 8 \boldsymbol{r}_{\text {root }}, 600<t \leqslant 1\;200 \\ \boldsymbol{r}_{\text {root }}\left[1+7 \sin \left(2 \pi \cdot \frac{t-2\;000}{2\;000}\right)\right], \\ 2\;000<t \leqslant 3\;000 \\ \boldsymbol{r}_{\text {root }}, \text { others } \end{array}\right. $ | (18) |
为了综合评估本文算法估计量测噪声RMS的性能,使用4种方案进行解算:1)SHKF1,本文改进的Sage-Husa算法,b=0.95;2)SHKF2,本文改进的Sage-Husa算法,b=0.9;3)SHKF3,本文改进的Sage-Husa算法,b=0.99;4)VBKF,变分贝叶斯估计算法。
图 1为不同方案对量测位置噪声RMS的估计,对速度噪声RMS的估计效果与之类似。可以看出:1)b接近于1时,估计曲线较为平滑,但是估计结果存在较为严重的拖尾效应,当b减小时,估计结果曲线存在较为严重的波动现象;2)SHKF1和VBKF的估计精度基本一致,即选择适当的b值时,本文算法对量测噪声RMS的估计精度与变分贝叶斯滤波相当;3)通过对滤波初始值的观测,本文算法对量测噪声RMS估计的初始值与b值无关,进而增强了算法的自适应性;4)本文算法不仅能够准确估计量测噪声RMS的突变,也能准确估计量测噪声RMS的缓变,自适应性较强;5)b取0.95左右时,估计精度最佳。

|
图 1 GNSS位置量测噪声RMS的跟踪图 Fig. 1 Tracking figures of GNSS position noise RMS |
基于上述仿真数据,图 2~3分别给出基于标准KF及本文算法(SHKF,b=0.95)的位置误差、速度误差对比图。可以看出,当量测噪声RMS发生变化时,相对于标准KF,本文算法能够提供更加精确的导航信息。

|
图 2 位置误差对比 Fig. 2 Comparison of position error |
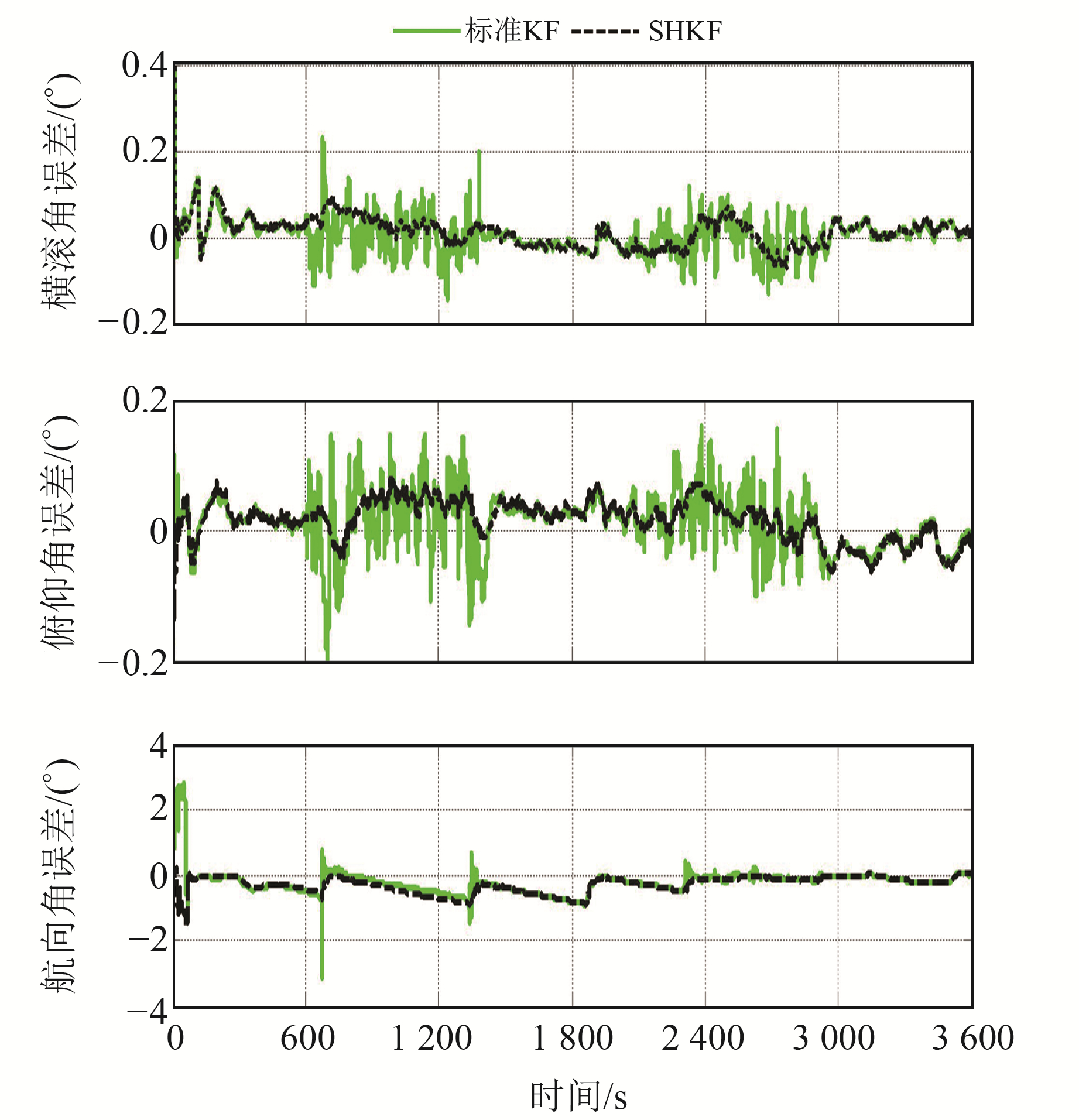
|
图 3 速度误差对比 Fig. 3 Comparison of velocity error |
为综合对比本文SHKF算法及标准KF的性能,将GNSS输出分为噪声RMS突变、缓变及恒定3个时段,分别对各导航参数误差的RMS进行统计(表 1)。可以看出,相对于标准KF,当GNSS噪声RMS突变时,SHKF算法可提高约18.8%的位置精度、约19%的速度精度;当GNSS噪声RMS缓变时,SHKF算法可提高约21%的位置精度、约23%的速度精度;当GNSS噪声RMS不变时,由SHKF算法得到的导航参数精度略低于标准KF,主要原因是由SHKF算法估计到的GNSS噪声RMS具有滞后性。同时,本文算法在执行过程中未发生滤波发散现象,克服了标准Sage-Husa自适应滤波算法在组合导航系统中存在的发散问题。
|
|
表 1 基于SHKF及标准KF的组合导航系统误差对比 Tab. 1 Error comparison of integrated navigation system based on SHKF and standard KF |
在量测噪声统计特性未知的情况下,为提高GNSS/SINS组合导航系统的滤波精度,提出一种改进的Sage-Husa自适应滤波方法。该方法能够实时、准确地估计量测噪声的未知RMS,且具有初始估计结果与遗忘因子无关、估计精度与变分贝叶斯方法相当的特点,同时克服了标准Sage-Husa自适应滤波方法存在的滤波发散问题。仿真实验表明,当量测噪声RMS发生变化时,本文方法明显优于常规卡尔曼滤波算法,有效提高了组合导航系统的滤波精度。
| [1] |
Xu S Q, Zhou H Y, Wang J Q, et al. SINS/CNS/GNSS Integrated Navigation Based on an Improved Federated Sage-Husa Adaptive Filter[J]. Sensors(Basel Switzerland), 2019, 19(17): 1-22
(  0) 0) |
| [2] |
邓传远. BDS/INS组合导航精确定位关键技术研究[D]. 合肥: 合肥工业大学, 2019 (Deng Chuanyuan. Research on Key Technologies Precise Location for BDS/INS Integrated Navigation[D]. Hefei: Hefei University of Technology, 2019)
(  0) 0) |
| [3] |
曾庆化, 赵天钰, 赵宾, 等. 基于指数渐消遗忘因子的组合导航自适应滤波算法[J]. 中国惯性技术学报, 2021, 29(3): 307-313 (Zeng Qinghua, Zhao Tianyu, Zhao Bin, et al. Adaptive Kalman Filter Algorithm Based on Exponential Attenuating Factor for Integrated Navigation System[J]. Journal of Chinese Inertial Technology, 2021, 29(3): 307-313)
(  0) 0) |
| [4] |
李宁, 祝瑞辉, 张勇刚. 基于Sage-Husa算法的自适应平方根CKF目标跟踪方法[J]. 系统工程与电子技术, 2014, 36(10): 1 899-1 905 (Li Ning, Zhu Ruihui, Zhang Yonggang. Adaptive Square CKF Method for Target Tracking Based on Sage-Husa Algorithm[J]. Systems Engineering and Electronics, 2014, 36(10): 1 899-1 905)
(  0) 0) |
| [5] |
Lim K L, Wang H. MAP Approximation to the Variational Bayes Gaussian Mixture Model and Application[J]. Soft Computing, 2018, 22(10): 3 287-3 299 DOI:10.1007/s00500-017-2565-z
(  0) 0) |
| [6] |
Lin X Y, Pan X L, Sun W W, et al. Multi-Scale Asynchronous Fusion Algorithm for Multi-Sensor Integrated Navigation System[J]. Proceedings of the Institution of Mechanical Engineers, Part Ⅰ: Journal of Systems and Control Engineering, 2022, 236(9): 1 709-1 723
(  0) 0) |
2. Naval Aeronautical University, Yantai 264001, China;
3. Shandong Nanshan Aluminum Co Ltd, 6 South-Nanshan Road, Yantai 265706, China
 2023, Vol. 43
2023, Vol. 43


