2. 大连理工大学建设工程学部,大连市凌工路2号,116024;
3. 山东农业大学机械与电子工程学院,山东省泰安市岱宗大街61号,271018
地面站要接收卫星数据,必须预报卫星位置并计算其高度角与方位角,以便地面站天线及时调整角度跟踪卫星并接收数据[1]。常用的轨道预报方法为广播星历与历书。广播星历可以提供卫星钟差、开普勒轨道参数与轨道摄动改正,由其确定的卫星位置精度较高,可用于定位计算。历书属于广播星历的概略形式,仅提供基本的轨道参数与钟差改正,由其确定的卫星位置精度较低,但是可以在较长时间内保持km级精度。然而,广播星历与历书的轨道预报误差均会随预报时间增长而迅速增大,尤其是广播星历,超过有效期后,轨道预报误差随时间呈膨胀型增长[2-3]。
北美防空司令部(North American Aerospace Defense Command,NORAD)对全球超过18 000个在轨物体进行探测、跟踪、编目与识别,以两行轨道根数(two-line element,TLE)的形式向全球公布,用于确定空间目标的位置与速度,并每天通过Spacetrack网站发布2次[4]。TLE星历不同于广播星历与历书,属于一种“平均轨道根数”,并采用特定方法去除周期扰动项[5]。TLE的生成算法未公开,因此需要结合NORAD公布的SGP4/SDP4模型才能进行卫星轨道的高精度预报[6]。其中,SGP4模型适用于近地目标(T < 225 min)的轨道预报,SDP4模型适用于高轨或深空目标(T>225 min)的轨道预报。故TLE星历结合SDP4模型可以进行BDS卫星轨道高精度预报[7],但目前这方面的研究较少。
针对上述情况,本文利用TLE星历结合SDP4模型预报BDS星座IGSO、GEO与MEO三类卫星30 d轨道,然后采用GFZ事后精密星历评估其预报精度,并与广播星历、历书的轨道预报精度进行对比分析,研究3种轨道预报方法的轨道预报精度特征及适用范围。
1 TLE星历与SDP4模型TLE星历的具体格式为:
1 AAAAAU YYLLLPPP BBBBB.BBBBBBBB. CCCCCCCC DDDDD-D EEEEE-E F GGGGZ
2 AAAAA HHH. HHHH III.IIII JJJJJJJ KKK. KKKK MMM. MMMM NN. NNNNNNNN RRRRZ
BDS星座卫星的轨道周期范围为771~1 432 min,均大于225 min,所以,基于TLE星历的BDS卫星轨道预报方法应选用SDP4模型,具体计算流程如图 1所示[8]。

|
图 1 基于SDP4模型的轨道预报算法流程 Fig. 1 The orbit prediction algorithm flow based on SDP4 model |
由于GEO与IGSO卫星是地球同步轨道卫星,所以需要轨道机动维持卫星轨道位置,且国际电信联盟(International Telecommunication Union,ITU)对GEO卫星的定点要求为优于0.1°,故GEO卫星轨道机动较为频繁。据统计,2019年BDS星座GEO卫星的轨道机动次数为6~16次。为此,本文将BDS卫星轨道预报时间设置为最长30 d(720 h)。
为了评估TLE星历结合SDP4模型预报BDS卫星轨道的精度,以目前在轨运行的IGSO1(PRN C06,NORAD 36828)、GEO5(PRN C05,NORAD 38091)与MEO3(PRN C11,NORAD 38250)卫星为例,预报2019-12-29~2020-01-31期间从星历参考时刻起约30 d(720 h) 的卫星轨道,然后选用GFZ事后精密星历评估轨道预报精度,并与广播星历、历书的轨道预报精度进行比较。
2.1 坐标系统转换由于TLE星历结合SDP4模型的BDS卫星轨道预报结果所属坐标系统为真赤道平春分点坐标系(true equator and mean equinox,TEME),与GFZ精密星历所属坐标系ITRS(ITRF2014)不一致,因此,在评估轨道预报精度时,还需要进行坐标系统的转换。TEME属于地心惯性坐标系,ITRS(ITRF2014)属于地心地固坐标系,所以TEME坐标系与ITRS(ITRF2014)坐标系的转换流程为:
1) 将TEME坐标系绕Z轴进行旋转,得到真赤道真春分点(true equator and equinox of date, TOD)坐标系,即瞬时真天球坐标系:
| $ \left(\begin{array}{l} X \\ Y \\ Z \end{array}\right)_{\text {TOD }}=R_Z(\Delta \psi \cos \varepsilon)\left(\begin{array}{l} X \\ Y \\ Z \end{array}\right)_{\mathrm{TEME}} $ | (1) |
式中,Δψ为黄经章动,表示由于章动而导致的黄经变化量;ε为黄赤交角。
2) 将瞬时真天球坐标系绕Z轴旋转GAST角,得到瞬时真地球坐标系,即准地固坐标系(pseudo Earth fixed,PEF):
| $ \left(\begin{array}{l} X \\ Y \\ Z \end{array}\right)_{\mathrm{PEF}}=R_Z(\mathrm{GAST})\left(\begin{array}{l} X \\ Y \\ Z \end{array}\right)_{\mathrm{TOD}} $ | (2) |
其中,瞬时真天球坐标系X轴与瞬时真地球坐标系X轴之间的夹角即为格林尼治真恒星时GAST。
3) 将瞬时真地球坐标系绕X轴旋转-Yp角,再绕Y轴旋转-Xp角,得到ITRS(ITRF2014)坐标系:
| $ \left(\begin{array}{c} X \\ Y \\ Z \end{array}\right)_{\text {ITRF2014 }}=R_Y\left(-X_p\right) R_X\left(-Y_p\right)\left(\begin{array}{c} X \\ Y \\ Z \end{array}\right)_{\mathrm{PEF}} $ | (3) |
式中,Xp与Yp为极移量。
2.2 评估结果分析以GFZ精密星历轨道作为参考标准,使用TLE星历、广播星历和历书计算3颗卫星的轨道预报误差,结果如图 2~4所示。其中,GEO5卫星轨道预报误差仅分析至约24 d(576 h),主要原因为2020-01-23 10:00:00~16:00:00期间GEO5卫星进行轨道机动,该时段卫星自主健康标识均为1。最后,统计3种轨道预报方法的轨道预报误差,结果如表 1所示。
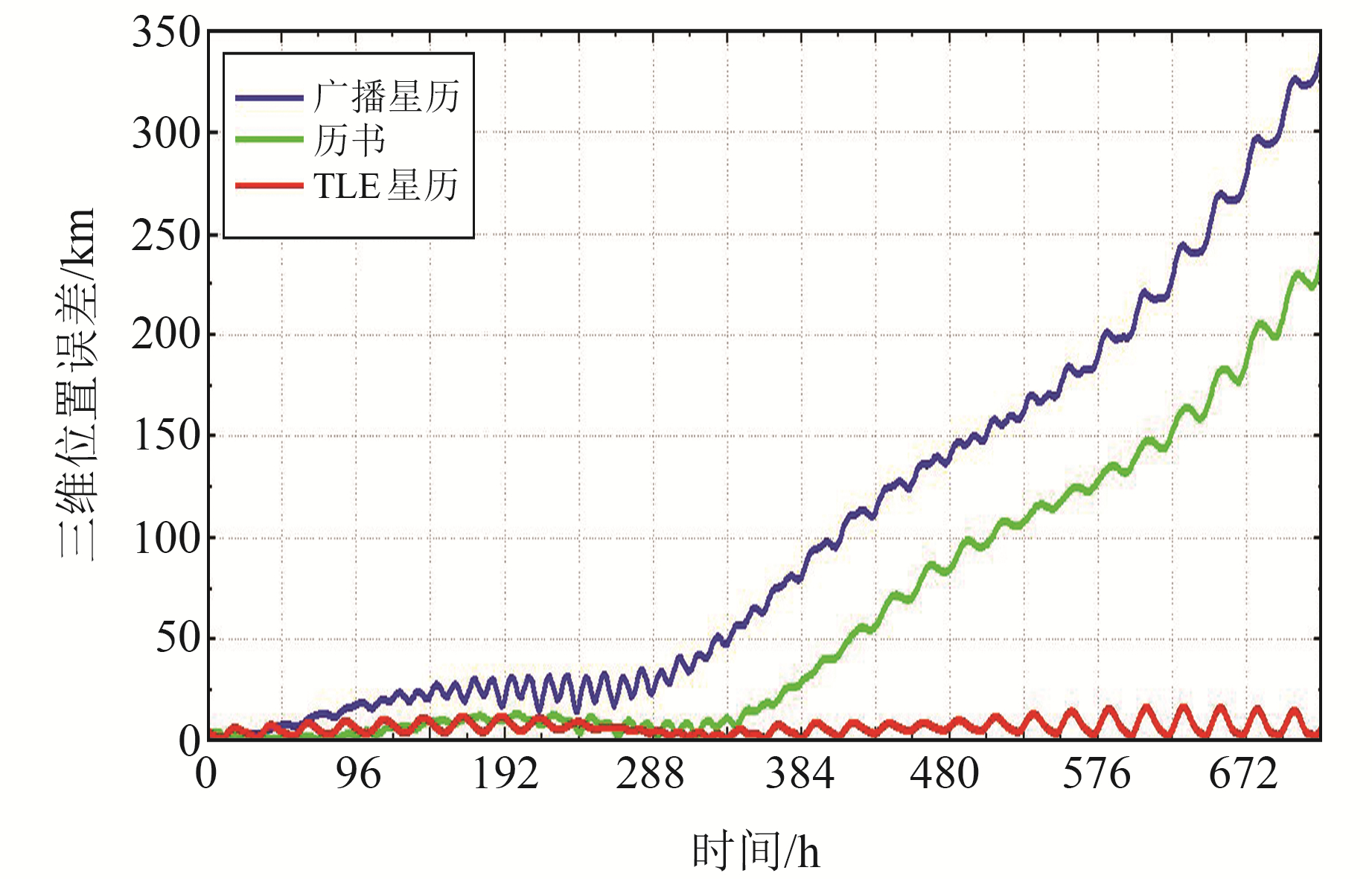
|
图 2 IGSO1卫星轨道预报的三维位置误差 Fig. 2 Three-dimensional position error of IGSO1 satellite orbit prediction |

|
图 3 GEO5卫星轨道预报的三维位置误差 Fig. 3 Three-dimensional position error of GEO5 satellite orbit prediction |
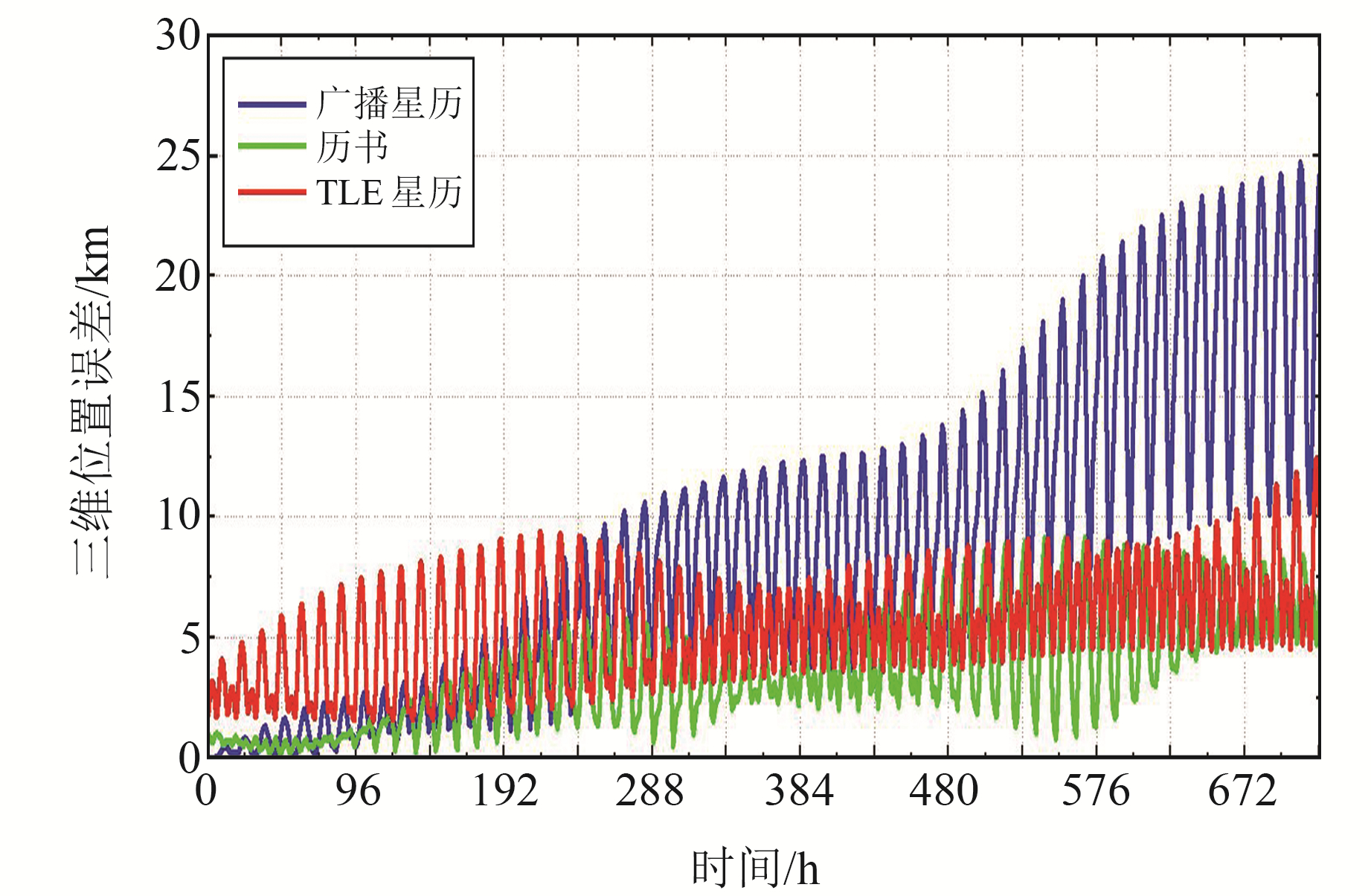
|
图 4 MEO3卫星轨道预报的三维位置误差 Fig. 4 Three-dimensional position error of MEO3 satellite orbit prediction |
|
|
表 1 3种方法的轨道预报误差 Tab. 1 The orbit prediction error of three methods |
对于IGSO1卫星轨道预报,在48 h内,广播星历、历书与TLE星历轨道预报的三维位置误差均小于8 km,其中广播星历的轨道预报精度最优。48 h后,广播星历预报的三维位置误差最先开始迅速增长,且大于历书与TLE星历。336 h后,历书预报的三维位置误差开始迅速增长,TLE星历预报的三维位置误差始终保持平稳趋势。至720 h时,广播星历与历书的轨道预报误差分别达到337.832 km与236.004 km,而TLE星历的最大轨道预报误差仅为16.552 km。
对于GEO5卫星轨道预报,在96 h内,广播星历、历书与TLE星历预报三维位置误差均小于16 km,且整体来看,广播星历与历书的轨道预报精度略优于TLE星历。96 h后,广播星历与历书预报三维位置误差迅速增长,且广播星历预报三维位置误差开始大于历书与TLE星历。192 h后,历书预报的三维位置误差开始大于TLE星历,TLE星历预报的三维位置误差始终保持微小的增长趋势,整体来看仍然较为平稳。广播星历至528 h、历书至576 h时,两者轨道预报误差分别达到240.155 km与199.567 km,而TLE星历的最大轨道预报误差仅为26.931 km。
对于MEO3卫星轨道预报,至720 h,广播星历预报的三维位置误差明显大于历书与TLE星历,TLE星历与历书的轨道预报精度基本相当,均小于13 km;然而,从历书的三维位置误差分布曲线中可以看到较为显著的线性增长趋势,而TLE星历的三维位置误差分布曲线则始终保持较为平稳的态势。
综合上述对比分析,可以得出如下结论:
1) 对于BDS的IGSO与GEO卫星,从短期的轨道预报结果来看,广播星历的轨道预报精度最优,TLE星历稍逊于广播星历与历书;从长期(30 d)的轨道预报结果来看,广播星历轨道预报精度最差,历书次之,TLE星历最优,且TLE星历的轨道预报精度明显比广播星历与历书高一个数量级。
2) 对于BDS的MEO卫星,从短期的的轨道预报结果来看,仍然是广播星历的轨道预报精度最优,TLE星历稍逊于广播星历与历书;从长期(30 d)的轨道预报结果来看,广播星历的轨道预报精度最差,历书与TLE星历的轨道预报精度基本相当,但TLE星历的轨道预报误差始终保持较为平稳的态势,历书的轨道预报误差则表现出显著的线性增长趋势。
为了验证上述结论,选取IGSO2(PRN C07,NORAD 37256)、GEO4(PRN C04,NORAD 37210)与MEO4(PRN C12,NORAD 38251)卫星TLE星历,预报2019-12-29~2020-01-31从星历参考时刻起约30 d(720 h)的卫星轨道,结果如图 5所示。可以看出,TLE星历在长期轨道预报中具有精度高、有效时间长、平稳性好等优势。

|
图 5 TLE星历轨道预报的三维位置误差 Fig. 5 Three-dimensional position error of TLE ephemeris orbit prediction |
然后,针对TLE星历的轨道预报结果,分别统计3类BDS卫星30 d内的轨道预报均方根(RMS)误差,结果如表 2所示。可以看出,利用TLE星历进行BDS卫星轨道预报时,GEO卫星精度最差,MEO与IGSO卫星精度基本相当。
|
|
表 2 BDS卫星TLE星历轨道预报误差RMS Tab. 2 TLE ephemeris orbit prediction error RMS of BDS satellites |
通过对比BDS卫星的轨道预报结果可以得出,在约30 d的长期轨道预报中,TLE星历显著优于广播星历与历书。在短期轨道预报中,TLE星历能够保持较高精度的轨道预报;在长期轨道预报中,TLE星历仍然能够保持一定的精度,主要是因为TLE星历属于平均轨道根数,能够恢复较长时间的卫星受力情况,因而能够维持稳定、高精度的轨道预报,验证了TLE星历结合SDP4模型在BDS卫星轨道预报中具有通用性强、有效时间长等优点。
3 BDS卫星轨道跟踪监测精度要求为了实现BDS卫星的轨道跟踪监测,必须保证地面站天线指向角正确,因此,BDS卫星的轨道预报误差直接决定了地面站天线接收BDS卫星信号的强度。对于高增益转台7.5 m天线,其对应的半功率波束宽度计算公式为[2-3]:
| $ 2 \theta_{0.5}=65 \lambda / D $ | (4) |
式中,λ为波长,λ=u/f,u=3.0×108 m/s为波速,f为频率;D为地面站天线直径;2θ0.5为半功率波束宽度,表示在归一化功率方向图的主瓣范围内,功率下降到主瓣最大值的一半(用功率表示时,即功率下降3 dB)的2个方向之间的夹角,如图 6所示。
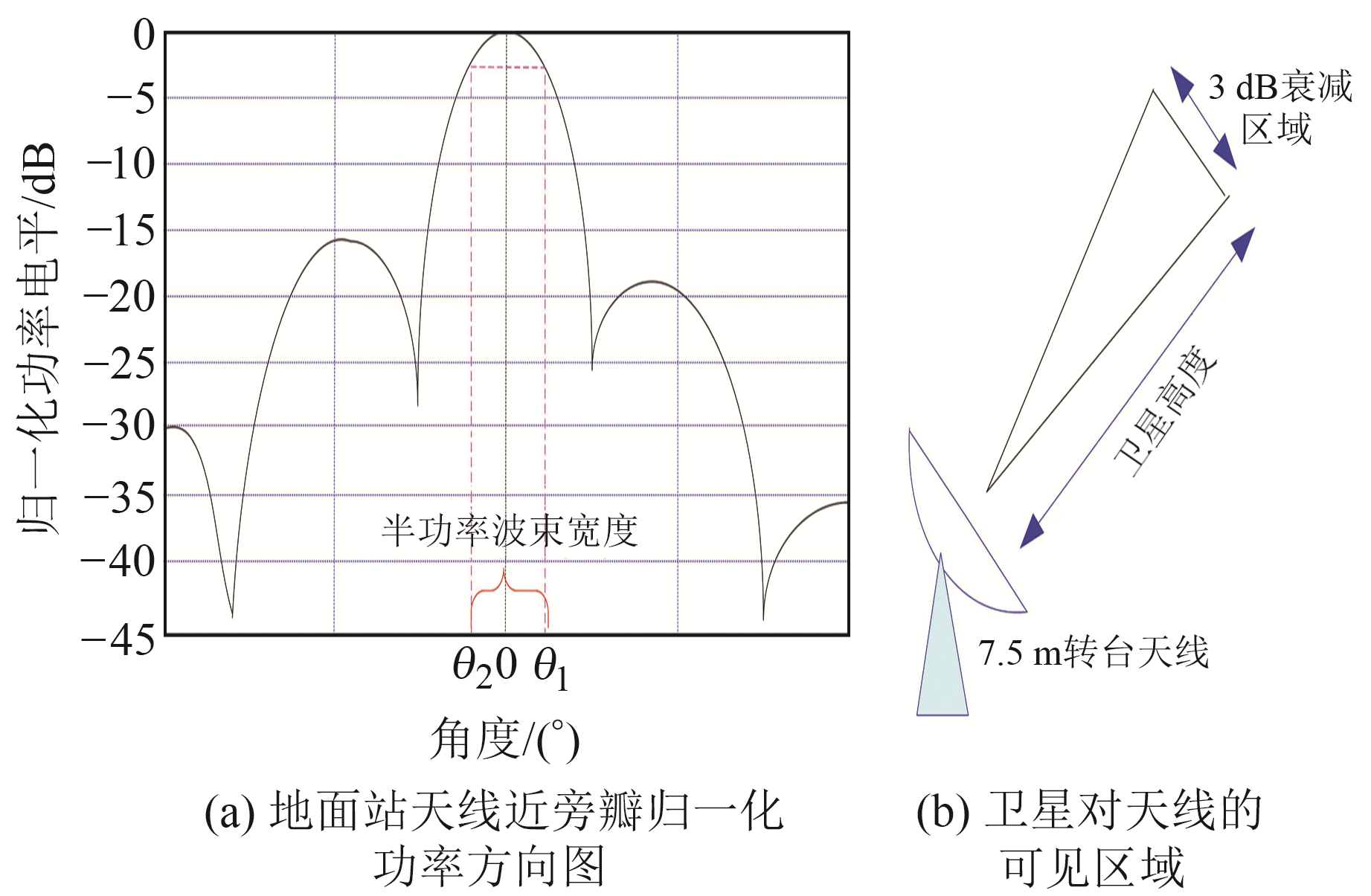
|
图 6 半功率波束宽度示意图 Fig. 6 The schematic diagram of half power beam width |
现阶段,北斗二号提供的公开服务信号分别为B1I(中心频率为1 561.098 MHz)、B2I(中心频率为1 207.140 MHz)与B3I(中心频率为1 268.520 MHz),北斗三号提供的公开服务信号分别为B1I、B1C(中心频率为1 575.42 MHz)、B2a(中心频率为1 176.45 MHz)、B2b(中心频率为1 207.14 MHz)与B3I。取BDS卫星信号的最大中心频率约1.5 GHz,按照式(4)计算其最小半功率波束宽度为2θ0.5=1.7°,即天线指向偏离卫星0.85°,信号就衰减3 dB,并且超过0.85°后,信号会加速衰减。因此,地面站天线为了实现对MEO、GEO与IGSO三类BDS卫星的跟踪监测,BDS卫星的轨道预报误差不能超过:
| $ \mathrm{d} r \leqslant r_{\min } \theta_{0.5} \Rightarrow \mathrm{d} r \leqslant 319 \mathrm{~km} $ | (5) |
式中,rmin为BDS星座的MEO、GEO与IGSO三类卫星的最低轨道高度,即21 528 km。
利用SDP4模型预报BDS星座3类卫星轨道,结果表明,GEO卫星轨道精度最差,MEO卫星与IGSO卫星轨道精度基本相当。为了验证SDP4模型的BDS卫星轨道预报精度能够满足轨道跟踪监测精度要求,选取轨道预报精度最差的GEO卫星,对全部GEO卫星进行约30 d的轨道预报,统计其三维位置误差的最大值e3D,结果如表 3所示。
|
|
表 3 GEO卫星TLE星历轨道预报误差 Tab. 3 TLE ephemeris orbit prediction error of GEO satellites |
根据BDS卫星轨道跟踪监测精度要求,BDS卫星轨道预报误差不能超过319 km。从表 3看出,即使是TLE星历轨道预报精度最差的GEO卫星也能够满足这个要求。综上,TLE星历结合SDP4模型的方法能够在长期轨道预报(30 d内)中兼顾BDS IGSO、GEO与MEO三类卫星轨道预报精度,并且能够满足BDS卫星轨道跟踪监测精度要求。
4 结语轨道预报是实现地面站跟踪监测BDS卫星的必要条件。本文利用TLE星历结合SDP4模型预报BDS星座IGSO、GEO与MEO三类卫星30 d轨道,并采用GFZ事后精密星历评估其轨道预报误差;然后,将该方法的轨道预报误差分别与广播星历、历书的轨道预报误差进行对比分析。结果表明,在短期轨道预报中,TLE星历能够保持较高精度的轨道预报;在长期轨道预报中,TLE星历精度显著优于广播星历与历书,并且能够兼顾BDS星座IGSO、GEO与MEO三类卫星轨道预报精度。主要原因为TLE星历属于平均轨道根数,能够恢复长时间的卫星受力情况,因而可以维持稳定、高精度的长期轨道预报。综上,TLE星历结合SDP4模型在BDS卫星轨道预报中具有通用性强、有效时间长等优点,能够满足BDS卫星轨道跟踪监测精度要求。
| [1] |
车通宇, 张传定, 杨力, 等. 北斗卫星轨道预报模型对比[J]. 测绘科学, 2015, 40(12): 91-96 (Che Tongyu, Zhang Chuanding, Yang Li, et al. Comparison and Analysis of BDS Satellites Orbit Prediction Models[J]. Science of Surveying and Mapping, 2015, 40(12): 91-96)
(  0) 0) |
| [2] |
车通宇, 杨力, 张传定, 等. SDP4模型用于北斗导航卫星轨道预报的精度分析[J]. 测绘地理信息, 2017, 42(2): 12-16 (Che Tongyu, Yang Li, Zhang Chuanding, et al. Accuracy Analysis for SDP4 Model Used in Beidou Navigation Satellites Orbit Prediction[J]. Journal of Geomatics, 2017, 42(2): 12-16)
(  0) 0) |
| [3] |
余小游, 覃曼丽, 吴问其, 等. 基于SDP4模型的导航卫星仰角及方位角预报[J]. 全球定位系统, 2014, 39(3): 44-48 (Yu Xiaoyou, Qin Manli, Wu Wenqi, et al. Navigation Satellite Elevation and Azimuth Prediction Based on SDP4 Model[J]. GNSS World of China, 2014, 39(3): 44-48)
(  0) 0) |
| [4] |
陈俊宇, 李彬, 桑吉章. 基于TLE数据的编目目标轨道改进及再编目[C]. 第2届中国空天安全会议, 大连, 2017 (Chen Junyu, Li Bin, Sang Jizhang. Orbit Improvement and Re-Cataloging of Catalogued Objects Based on TLE Data[C]. The Second China Aerospace Safety Conference, Dalian, 2017)
(  0) 0) |
| [5] |
刘劲宏. 基于TLE数据的空间目标大气再入预报[J]. 测绘学报, 2021, 50(5): 707 (Liu Jinhong. Prediction of Atmospheric Reentry of Space Objects Based on TLE Data[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(5): 707)
(  0) 0) |
| [6] |
Xu X L, Xiong Y Q. Study on the Orbit Prediction Errors of Space Objects Based on Historical TLE Data[J]. Chinese Astronomy and Astrophysics, 2019, 43(4): 563-578 DOI:10.1016/j.chinastron.2019.11.007
(  0) 0) |
| [7] |
张栩晨, 杜兰, 刘泽军, 等. 基于TLE时序的GEO目标东西机动预报[J]. 测绘科学技术学报, 2021, 38(4): 337-342 (Zhang Xuchen, Du Lan, Liu Zejun, et al. TLE-Based East-West Maneuver Forecast of GEOs[J]. Journal of Geomatics Science and Technology, 2021, 38(4): 337-342)
(  0) 0) |
| [8] |
Hoots F R, Roehrich R L. Models for Propagation of NORAD Element Sets[J]. Spacetrack Report, 1988(3)
(  0) 0) |
2. Faculty of Infrastructure Engineering, Dalian University of Technology, 2 Linggong Road, Dalian 116024, China;
3. College of Mechanical and Electronic Engineering, Shandong Agricultural University, 61 Daizong Street, Tai'an 271018, China
 2023, Vol. 43
2023, Vol. 43


