2. 北斗导航应用技术协同创新中心,郑州市科学大道62号,450001
目前应用最广泛的模糊度固定方法是基于整数最小二乘原则在模糊度域中确定模糊度的最小二乘模糊度去相关算法LAMBDA[1]。LAMBDA算法主要包括3个步骤:模糊度降相关、模糊度搜索、模糊度检验。其中,模糊度降相关涉及大量矩阵运算,耗时较长,因此有必要对其降相关过程进行研究,提高计算效率。国内外学者对降相关过程进行了大量研究:Liu等[2]基于上下三角过程构造联合去相关算法;Xu[3]使用Cholesky分解法构建整数高斯矩阵,在高维情况下分解得到条件数最小的浮点解协方差矩阵;陈树新[4]提出一种以降低协方差矩阵条件数为准则的模糊度去相关算法;Liu等[5]克服了Z变换可能带来的矩阵病态分解,减少了20%的解算时间;安向东等[6]根据频间偏差率范围,采用搜索方法和线性模型去除相位频间偏差对宽窄巷模糊度的影响;邱蕾等[7]提出在位移值较大的情况下通过多种载波相位组合方法解算短基线GPS整周模糊度。自从Hassibi等[8]将格理论中的规约算法Lenstra-Lenstra-Lovász(LLL) 应用于模糊度降相关以来,诸多学者从格基规约理论出发分析LLL的降相关性能:Xu[9]提出一种性能优于整数高斯去相关算法和LLL算法的逆整数Cholesky去相关方法;范龙[10]基于分块Gram-Schmidt正交化算法改进LLL算法;谢恺等[11]基于系统旋转的Houscholder正交变换对LLL算法进行改进;卢立果[12]采用分块降维方法改进LLL算法。
上述方法中,Cholesky去相关法效果较好,但也存在一定的缺陷:1) L、D、LT子矩阵的形成过程过于复杂;2)在实际编程计算中,L、D、LT矩阵元素需要较多的存储矩阵;3)各矩阵元素只能按顺序求出;4)未能有效利用各子矩阵元素之间的关系。基于此,本文提出一种改进的M-Cholesky分解法,用合成矩阵取代L、D、LT矩阵,简化了L、D、LT子矩阵的关系;之后,利用高斯算法中的四角规则计算各子矩阵元素,提升分解时的解算效率,可减少约40%的计算元素个数。
1 基于Cholesky分解的模糊度去相关模型GNSS观测方程的模型求解可以等价于求解下式的最小值问题:
| $ \min\limits_{\check{{a}}}(\hat{\boldsymbol{a}}-\check{\boldsymbol{a}})^{\mathrm{T}} \boldsymbol{Q}_{\hat{a}}^{-1}(\hat{\boldsymbol{a}}-\check{\boldsymbol{a}}), \check{\boldsymbol{a}} \in \boldsymbol{Z}^n $ | (1) |
式中,
由于模糊度分量之间通常具有很高的相关性,因此搜索效率较低。为了使求解过程更高效,可以通过整数高斯变换(Z变换)将其转化为新的最小二乘问题:
| $ \min\limits_z(\boldsymbol{z}-\hat{\boldsymbol{z}})^{\mathrm{T}} \boldsymbol{Q}_{\hat{{z}}}^{-1}(\boldsymbol{z}-\hat{\boldsymbol{z}}), \boldsymbol{z} \in \boldsymbol{Z}^n $ | (2) |
| $ \boldsymbol{z}=\boldsymbol{Z}^{\mathrm{T}} \boldsymbol{a}, \hat{\boldsymbol{z}}=\boldsymbol{Z}^{\mathrm{T}} \hat{\boldsymbol{a}}, \boldsymbol{Q}_{\hat{{z}}}=\boldsymbol{Z}^{\mathrm{T}} \boldsymbol{Q}_a \boldsymbol{Z} $ | (3) |
式中,Z为幺模矩阵,即矩阵的行列式为1。矩阵Z的元素均为整数。
利用下三角Cholesky对
| $ \boldsymbol{Q}_{\hat{a}}=\boldsymbol{L}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{L}, \boldsymbol{Q}_{\hat{z}}=\boldsymbol{Z}^{\mathrm{T}} \boldsymbol{L}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{L} \boldsymbol{Z}=\overline{\boldsymbol{L}}^{\mathrm{T}} \overline{\boldsymbol{D}} \overline{\boldsymbol{L}} $ | (4) |
式中,L和L为单位下三角矩阵,D和D为对角矩阵且对角线元素均大于0。Z的构造方程为:
| $ \boldsymbol{Z}=\boldsymbol{I}-\eta \boldsymbol{e}_i \boldsymbol{e}_j^{\mathrm{T}} $ | (5) |
式中,I为n维单位矩阵,η为对L矩阵的第i行第j列的元素取整,ei和ej为单位坐标向量。
2 M-Cholesky分解算法传统Cholesky分解模型复杂,且需要4个数组分别存放Q、LT、D、L矩阵。本文通过研究矩阵间各元素的相应关系,引入合成矩阵来减少计算所需的数组,并结合高斯算法中的四角规则提出一种改进的M-Cholesky分解法。
以4阶矩阵Q为例,给出其Cholesky分解:
| $ \begin{array}{*{20}{c}} & \boldsymbol{Q}=\left[\begin{array}{llll} q_{11} & q_{12} & q_{13} & q_{14} \\ q_{21} & q_{22} & q_{23} & q_{24} \\ q_{31} & q_{32} & q_{33} & q_{34} \\ q_{41} & q_{42} & q_{42} & q_{44} \end{array}\right]= \\ & {\left[\begin{array}{cccc} 1 & l_{12} & l_{13} & l_{14} \\ & 1 & l_{23} & l_{24} \\ & & 1 & l_{34} \\ & & & 1 \end{array}\right] \cdot\left[\begin{array}{llll} d_{11} & & & \\ & d_{22} & & \\ & & d_{33} & \\ & & & d_{44} \end{array}\right] \cdot} \\ & {\left[\begin{array}{cccc} 1 & & & \\ l_{21} & 1 & & \\ l_{31} & l_{32} & 1 & \\ l_{41} & l_{42} & l_{43} & 1 \end{array}\right]} \\ & \end{array} $ | (6) |
将LT、D、L矩阵整合得到的合成矩阵与Q矩阵各元素进行比较,合成矩阵与Q矩阵的对应元素关系如式(7)中的合成矩阵所示:
| $ \begin{array}{*{20}{c}} {\left[\begin{array}{cc} d_{11}=q_{11}-\left(d_{22} l_{12} l_{21}+d_{33} l_{13} l_{31}+d_{44} l_{14} l_{41}\right) & l_{12}=\left(q_{12}-d_{33} l_{13} l_{32}-d_{44} l_{14} l_{42}\right) / d_{22} \\ l_{21}=\left(q_{21}-d_{33} l_{23} l_{31}-d_{44} l_{24} l_{41}\right) / d_{22} & d_{22}=q_{22}-\left(d_{33} l_{23} l_{32}+d_{44} l_{24} l_{42}\right) \\ l_{31}=\left(q_{31}-d_{44} l_{34} l_{41}\right) / d_{33} & l_{32}=\left(q_{32}-d_{44} l_{34} l_{42}\right) / d_{33} \\ l_{41}=q_{41} / d_{44} & l_{42}=q_{42} / d_{44} \end{array}\right.}\\ {\left.\begin{array}{cc} l_{13}=\left(q_{13}-d_{44} l_{14} l_{43}\right) / d_{33} & l_{14}=q_{14} / d_{44} \\ l_{23}=\left(q_{23}-d_{44} l_{24} l_{43}\right) / d_{33} & l_{23}=q_{24} / d_{44} \\ d_{33}=q_{33}-d_{44} l_{34} l_{43} & l_{34}=q_{34} / d_{44} \\ l_{43}=q_{43} / d_{44} & d_{44}=q_{44} \end{array}\right]} \end{array} $ | (7) |
可以看出:1)利用式(7)进行Cholesky分解时,可在Q矩阵的基础上直接计算得到合成矩阵,仅需要1个数组即可存放原本需要3个数组存储的内存;2)合成矩阵中的元素lij与lji关于主对角线元素对称相等,因此在进行Cholesky分解时,可以仅计算对角线元素以上的lij元素,lji=lij。
在上述分析的基础上,利用四角规则给出M-Cholesky算法中合成矩阵元素的计算步骤:
1) 基于dii对第i行元素进行规约化处理,得到lij元素;
2) 将lji、l′ij代入qij(k)的计算式中进行消元处理得到qij(k),其中仅有dii=qiik完成计算(k为计算次数);
3) 将第i行的lij赋值给第i列的lji元素;
4) 对(i-1), (i-2), …, 1行依次循环,完成所有计算。
其中,步骤2)中参与计算的元素为:
| $ \left[\begin{array}{ccccc} \cdots & a_{j k}^{(i-1)}\left(a_{j k}^{(i)}\right) & \cdots & l_{j i}^{\prime}\left(l_{j i}\right) & \cdots \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ \cdots & l_{i j} & \cdots & d_{i i} & \cdots \end{array}\right] $ | (8) |
式中,dii为对角线元素,lij为始终位于对角线所在行以左的交叉元素,l′ji(lji)为始终位于对角线元素所在列以上的消元元素,括号内外为赋值前后的值,ajk(i-1)(ajk(i))为消元元素所在行与交叉元素所在列的交叉点上的计算元素,括号内外为计算前后的值,根据其所在位置可转化为相应的dii、lij、l′ji(lji)元素。
由式(8)可以看出,每次参与合成矩阵计算的4个元素均位于矩形的4个角上,因此称之为四角规则。在M-Cholesky算法计算过程中,所有计算元素转换为相应的对角元素、交叉元素和消元元素时,最多只用到3个元素,因此可以将该计算过程视为规约化后的消元计算。M-Cholesky算法与Cholesky算法在计算过程中所需的计算元素个数如表 1所示。
|
|
表 1 M-Cholesky算法与Cholesky算法所需计算元素个数对比 Tab. 1 Comparison of numbers of computing elements required by M-Cholesky algorithm and Cholesky algorithm |
由表 1可见,M-Cholesky算法可减少约40%的计算元素,提高了计算效率,且不影响计算结果的精度。
3 实验验证解算精度与时间效率是判断一个模糊度解算算法是否可行的关键,但由于本文所提出的M-Cholesky算法仅改变了计算元素,并不影响定位精度,因此仅采用仿真数据与实测数据对Cholesky算法与M-Cholesky算法的运行时间进行比较。
本文基于Microsoft Visual Studio 2019,利用C语言进行M-Cholesky算法的程序设计,并进行数值模拟测试。所有计算均在Windows 10操作系统的电脑平台上进行,处理器为16 GB内存的Intel(R) Core(TM) i7-8750H CPU@ 2.20 Hz。
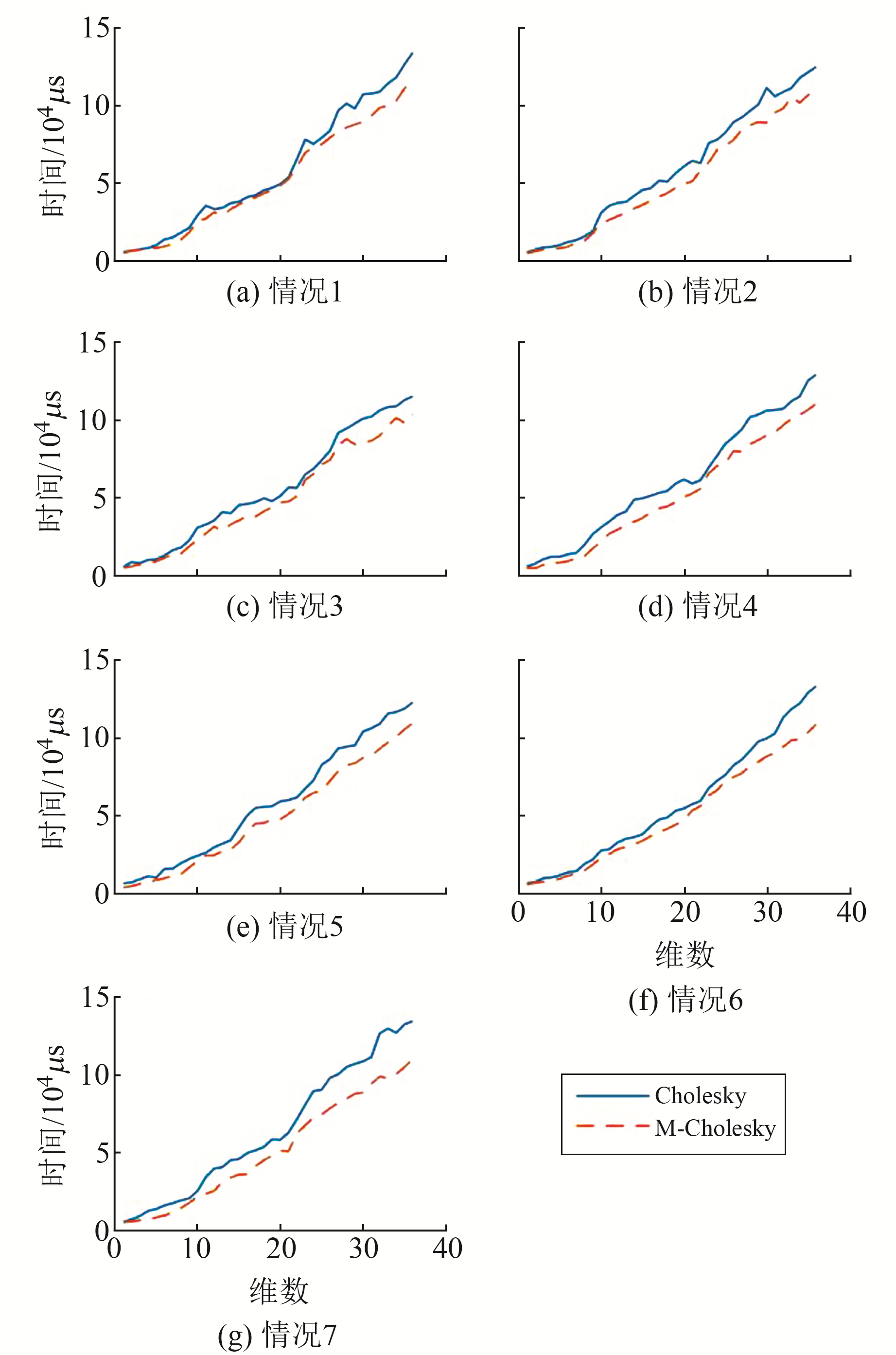
3.1 仿真实验参照文献[13]的仿真参数进行仿真实验,仿真维数为5~40。为避免偶然情况的出现,每次仿真实验取100次均值。2种算法的平均运行时间如图 1所示,所有情况下40维的平均运行时间如表 2所示。
|
图 1 平均运行时间 Fig. 1 Average running time |
|
|
表 2 40维解算时间对比 Tab. 2 Comparison of 40 dimensional solution time |
由图 1可见,在观测维数为5~40的情况下,2种方法的计算时间虽然偶尔有波动,但整体上都随维数的增加而增加,其中M-Cholesky算法计算时间总体低于Cholesky算法,且计算效率也随维数的增加而提升。由表 2可见,M-Cholesky算法的计算时间更短,相比于Cholesky算法,情况1~7中,M-Cholesky算法计算时间分别提升10.6%、13.5%、12.5%、16%、15.7%、13.5%、20.3%。
3.2 实测实验实测实验分为3组:1)短基线组采用和芯星通UB4B0-MINI板卡采集的静态观测数据,基线长89.83 m,采样间隔1 s,截取3 000个历元对解算时间和结果进行分析;2)中长基线组采用武汉大学IGS数据中心下载的香港地区HKSL和HKWS站的IGS数据,2站构成的基线长度为42.51 km,采样间隔30 s;3)长基线组采用武汉大学IGS数据中心下载的香港地区HKSL和武汉地区JFNG站的IGS数据,2站构成的基线长度为903.26 km,采样间隔30 s。所使用的数据均为标准RINEX格式数据,包括星历数据和观测数据。
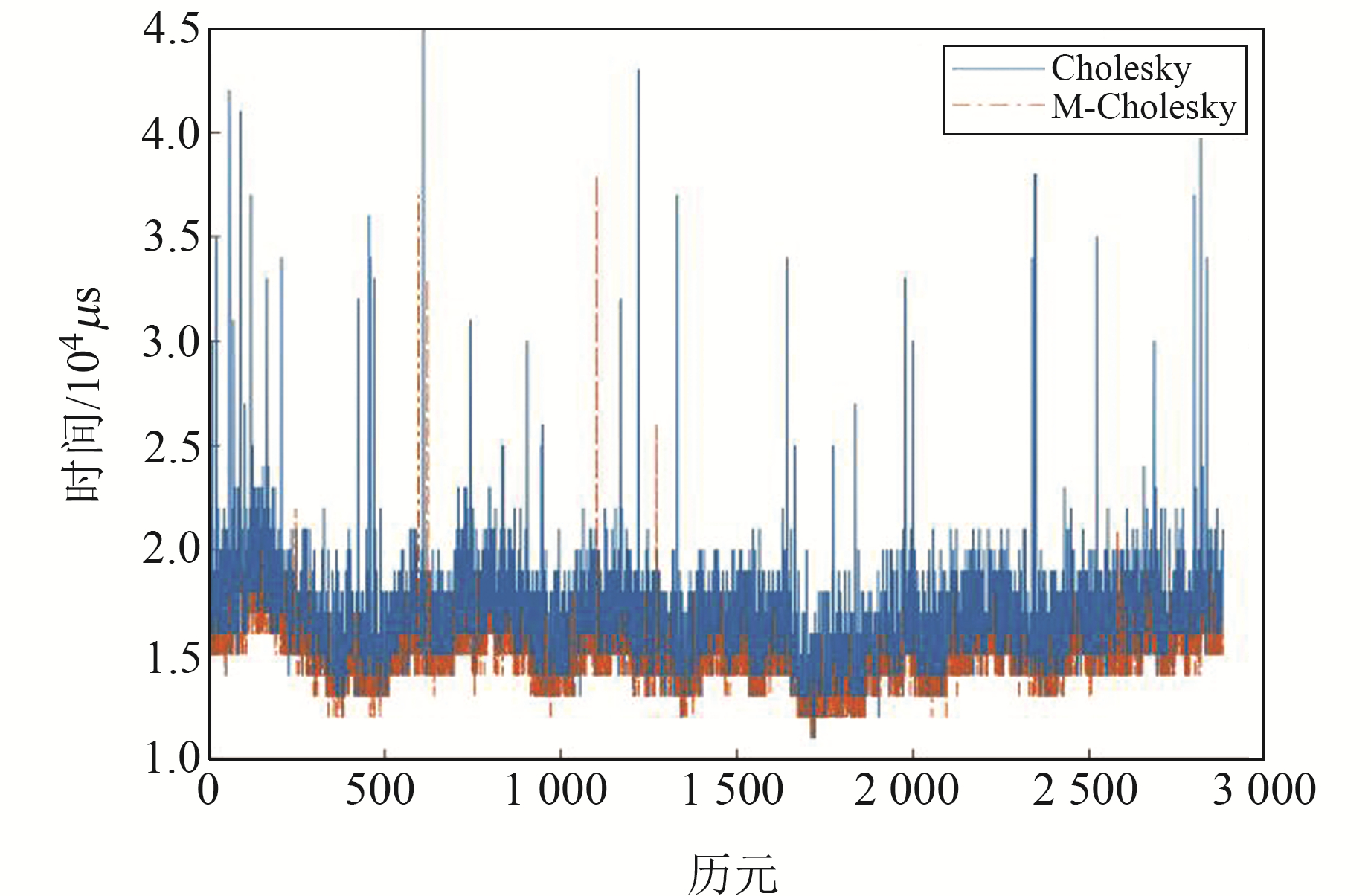
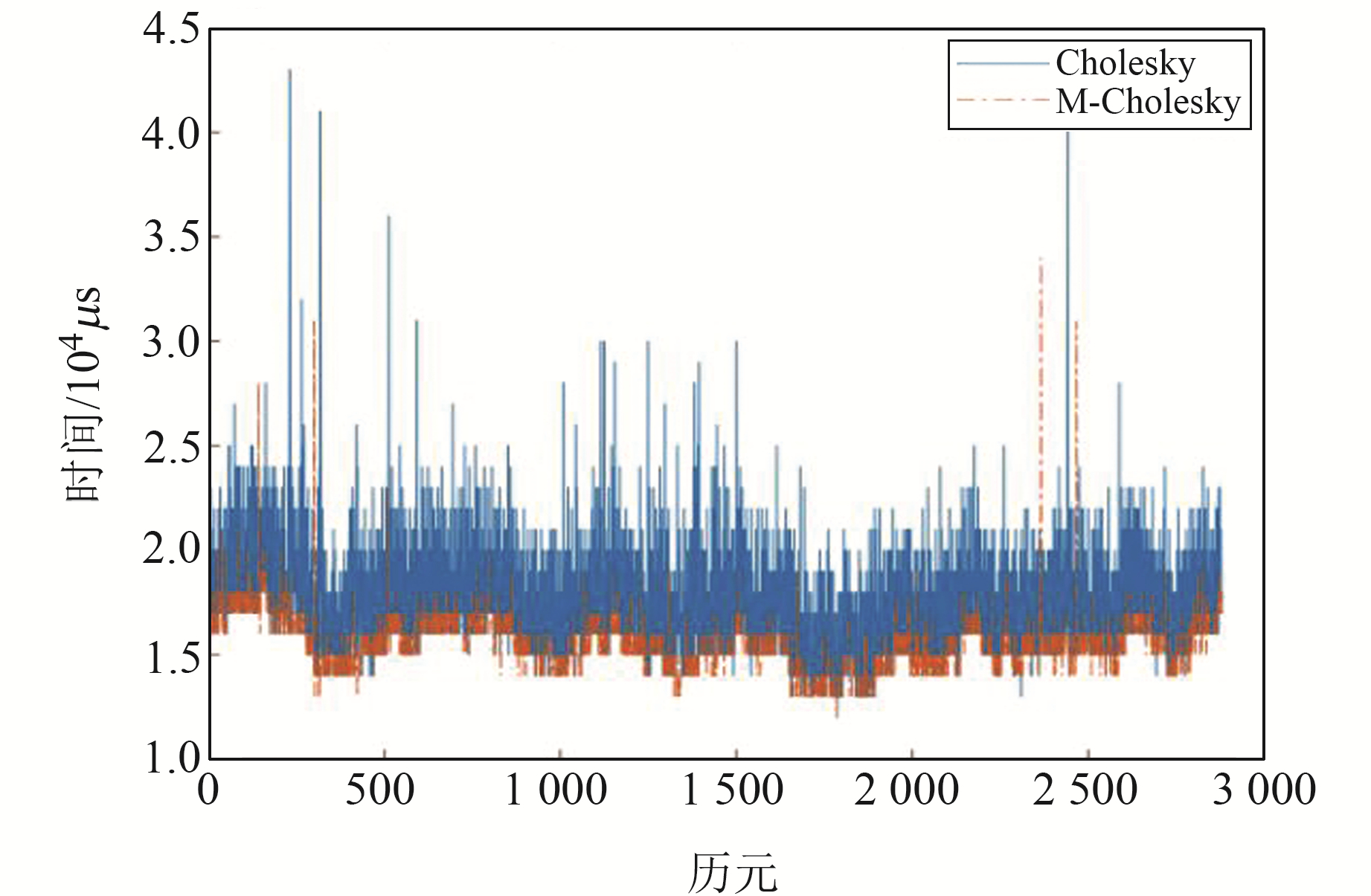
采用GPS、BDS、Galileo、GLONASS多系统数据进行整周模糊度融合解算,3种基线解算时间对比情况如图 2~4所示。

|
图 2 短基线解算时间对比 Fig. 2 Comparison of short baseline solution time |
|
图 3 中长基线解算时间对比 Fig. 3 Comparison of medium baseline solution time |
|
图 4 长基线解算时间对比 Fig. 4 Comparison of long baseline solution time |
由图 2可见,Cholesky算法的解算时间大致在(1.6~1.8)×104 μs之间,而本文提出的M-Cholesky算法解算时间大致在(1.5~1.7)×104 μs之间,所需解算时间较少,且M-Cholesky算法的整周模糊度解算结果相对稳定。由图 3、4也可以看出,M-Cholesky算法在解算时间和解算稳定性上表现更好。需要说明的是,短基线实验结果是从观测到的17 570个历元中截取的3 000个历元,采样间隔为1 s,而中长、长基线的观测时段长于短基线,采样间隔均为30 s,因此图 2解算时间曲线较图 3、4更平缓。
4 结语本文分析影响Cholesky算法计算效率的因素,引入四角规则,提出一种改进的M-Cholesky算法。实验结果表明,相对于Cholesky算法,M-Cholesky算法求解模糊度的计算时间减少约15%,提高了整周模糊度固定的效率,且解算精度与Cholesky算法一致。
如何处理四角规则中分母为0或接近0时的特殊情况,是完善M-Cholesky算法需要进一步考虑的问题。
| [1] |
Teunissen P J G. The Least-Squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82 DOI:10.1007/BF00863419
(  0) 0) |
| [2] |
Liu L T, Hsu H T, Zhu Y Z, et al. A New Approach to GPS Ambiguity Decorrelation[J]. Journal of Geodesy, 1999, 73(9): 478-490 DOI:10.1007/PL00004003
(  0) 0) |
| [3] |
Xu P L. Random Simulation and GPS Decorrelation[J]. Journal of Geodesy, 2001, 75(7): 408-423
(  0) 0) |
| [4] |
陈树新. GPS整周模糊度动态确定的算法及性能研究[D]. 西安: 西北工业大学, 2002 (Chen Shuxin. A Study of the Algorithm and Its Performance for GPS Ambiguity Resolution on the Fly[D]. Xi'an: Northwest Polytechnical University, 2002)
(  0) 0) |
| [5] |
Liu Z K, Huang S J. Research on Ambiguity Resolution Aided with Triple Difference[J]. Journal of Systems Engineering and Electronics, 2008, 19(6): 1 090-1 096 DOI:10.1016/S1004-4132(08)60202-9
(  0) 0) |
| [6] |
安向东, 陈华, 姜卫平, 等. 长基线GLONASS模糊度固定方法及实验分析[J]. 武汉大学学报: 信息科学版, 2019, 44(5): 690-698 (An Xiangdong, Chen Hua, Jiang Weiping, et al. GLONASS Ambiguity Resolution Method Based on Long Baselines and Experimental Analysis[J]. Geomatics and Information Science of Wuhan University, 2019, 44(5): 690-698)
(  0) 0) |
| [7] |
邱蕾, 花向红, 蔡华, 等. GPS短基线整周模糊度的直接解法[J]. 武汉大学学报: 信息科学版, 2009, 34(1): 97-99 (Qiu Lei, Hua Xianghong, Cai Hua, et al. Direct Calculation of Ambiguity Resolution in GPS Short Baseline[J]. Geomatics and Information Science of Wuhan University, 2009, 34(1): 97-99)
(  0) 0) |
| [8] |
Hassibi A, Boyd S. Integer Parameter Estimation in Linear Models with Applications to GPS[J]. IEEE Transactions on Signal Processing, 1998, 46(11): 2 938-2 952 DOI:10.1109/78.726808
(  0) 0) |
| [9] |
Xu P L. Parallel Cholesky-Based Reduction for the Weighted Integer Least Squares Problem[J]. Journal of Geodesy, 2012, 86(1): 35-52 DOI:10.1007/s00190-011-0490-y
(  0) 0) |
| [10] |
范龙. 基于格理论的GNSS模糊度估计方法研究[D]. 郑州: 信息工程大学, 2013 (Fan Long. Research on Method of Integer Ambiguity Estimation with Lattice Theory[D]. Zhengzhou: Information Engineering University, 2013)
(  0) 0) |
| [11] |
谢恺, 柴洪洲, 范龙, 等. 一种改进的LLL模糊度降相关算法[J]. 武汉大学学报: 信息科学版, 2014, 39(11): 1 363-1 368 (Xie Kai, Chai Hongzhou, Fan Long, et al. An Improved LLL Ambiguity Decorrelation Algorithm[J]. Geomatics and Information Science of Wuhan University, 2014, 39(11): 1 363-1 368)
(  0) 0) |
| [12] |
卢立果. GNSS整数最小二乘模糊度解算理论与方法研究[J]. 测绘学报, 2017, 46(9): 1 204 (Lu Liguo. Study on Theory and Method of GNSS Integer Least Squares Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(9): 1 204)
(  0) 0) |
| [13] |
Chang X W, Yang X, Zhou T. MLAMBDA: A Modified LAMBDA Method for Integer Least-Squares Estimation[J]. Journal of Geodesy, 2005, 79(9): 552-565 DOI:10.1007/s00190-005-0004-x
(  0) 0) |
2. Collaborative Innovation Center of BDS Research Application, 62 Kexue Road, Zhengzhou 450001, China
 2023, Vol. 43
2023, Vol. 43


