2. 安徽理工大学矿区环境与灾害协同监测煤炭行业工程研究中心,安徽省淮南市泰丰大街168号,232001;
3. 安徽理工大学矿山采动灾害空天地协同监测与预警安徽普通高校重点实验室,安徽省淮南市泰丰大街168号,232001
对流层延迟是信号在对流层中传播产生的误差,对GNSS导航定位、GNSS气象学、灾害预防等研究具有重要意义,可用对流层天顶总延迟(ZTD)和与高度角相关的投影函数的乘积表示[1-2]。ZTD是GNSS气象学中大气可降水量(PWV)反演的基础[3-4],其与信号频率无关,无法利用多频观测进行改正,一般通过区域模型改正来削弱其对GNSS定位的影响[5]。建立稳定可靠的ZTD模型是GNSS研究的热点之一[6]。区域ZTD模型分为依赖实测气象参数的经典模型和无需气象参数的经验模型,其中经典模型对于难以获取实测气象参数的区域具有局限性,而经验模型适用范围广、使用方便,但精度有限[7-8]。
近年来,机器学习方法因其能解决分类和预测等问题,且具有强大的非线性拟合能力,在区域ZTD建模、GNSS气象学等研究领域具有潜在优势,备受学者青睐[9-11]。鉴于部分经验模型精度较差,无法满足高精度的需求,本文基于GPT2w和UNB3m模型的ZTD预测值[12-14],利用机器学习方法提高模型预测精度。分别将这两种区域ZTD经验模型得到的ZTD值作为背景数据[14-16],连同测站的经纬度和大地高等数据一同作为模型输入参数,采用RF和BPNN两种机器学习方法分别建立ZTD区域改进模型,并对2种模型的拟合精度和预测精度进行对比分析。本文研究成果可为经验ZTD模型改进、区域ZTD建模、GNSS实时精密定位和水汽反演等研究提供一定的理论与方法参考。
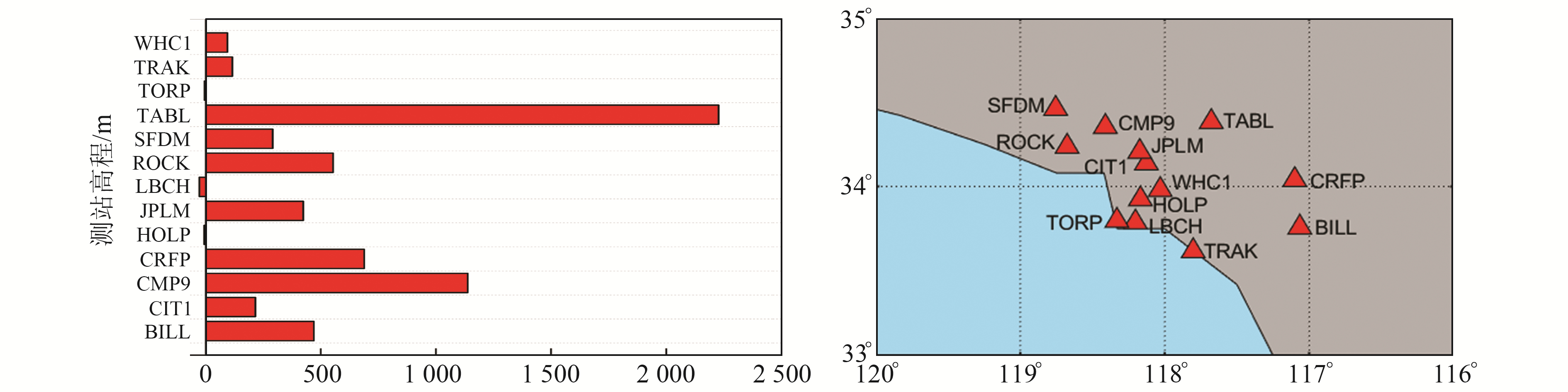
1 建模数据来源及处理本文利用美国加利福尼亚州南部13个IGS站的观测数据,以GAMIT软件解算的ZTD值作为参考值[17],测站平面和高程分布如图 1所示,测站的纬度、经度和大地高数据可从IGS官网(https://mgex.igs.org/network)获取。利用GAMIT软件对13个测站2021年doy183~213的RINEX观测数据进行解算,解算过程中引入2个长距离IGS测站(BREW和NLIB)以提高解算精度,得到分辨率为1 h的ZTD解算数据ZTD_GAMIT,将其作为真值。将美国加州13个IGS测站的经纬度等信息代入GPT2w和UNB3m模型,分别计算2种模型对应的ZTD值并作为背景数据:ZTD_GPT和ZTD_UNB。将CIT1测站的ZTD_GAMIT值用于模型精度检验,其余12个测站的纬度、经度、大地高、背景数据、时间信息和ZTD_GAMIT值用于建模。为降低数据的数量级并提高机器学习模型的训练速度,对上述数据进行归一化处理,并在得到结果后对其进行反归一化处理还原成原数量级。
|
图 1 IGS测站高程与位置 Fig. 1 Elevation and location of IGS stations |
研究表明,ZTD受纬度B、经度L、大地高H及时间因素的共同影响,因此本文构造的2种基于机器学习的区域ZTD模型将上述因素连同背景数据ZTD_GPT或ZTD_UNB一同作为自变量,预测值ZTDpre为因变量。通过机器学习方法,自变量和因变量之间的关系可以表示为:
| $\mathrm{ZTD}_{\mathrm{pre}}=\varphi\left(B, L, H, \text { doy, } h, \mathrm{ZTD}_{\text {model }}\right)$ | (1) |
式中,φ(·)为机器学习模型,doy为年积日,h为每日小时数(0~23 h),ZTDmodel为背景数据,即ZTD_GPT或ZTD_UNB。
2.1 RF建模原理RF是一种较新的机器学习模型[18],主要应用于分类和回归问题。RF本质上属于集成学习方法,通过结合多个决策树进行回归预测,最大优势在于能在复杂环境变量中找到因变量与多个自变量之间的非线性关系,并对其进行拟合以达到最佳预测效果[19]。本文采用分类回归树(CART)的决策树算法,该算法采用递归划分方法,将训练数据划分为多个同构子集,并基于确定性算法与每个子集建立多元回归树。具体过程为:先从训练数据中选择包含大约2/3样本的Bootstrap样本;然后在每个节点上随机选择输入变量,利用二叉分割递归将输入空间依次划分为更小的区域,从而使回归树生长。对于回归树,通过最小化回归误差来确定分裂点,回归误差为各子集回归误差的加权和。通过在许多单独的回归树中引入随机性,并对去相关的这些个体树的大量集合进行平均,输出的预测值可表示为:
| $\varphi(X)=\frac{1}{B} \sum\limits_{b=1}^B T_b(X)$ | (2) |
式中,X为输入变量,φ为随机森林模型的最终输出,Tb为每棵回归树的输出,B为回归树个数。
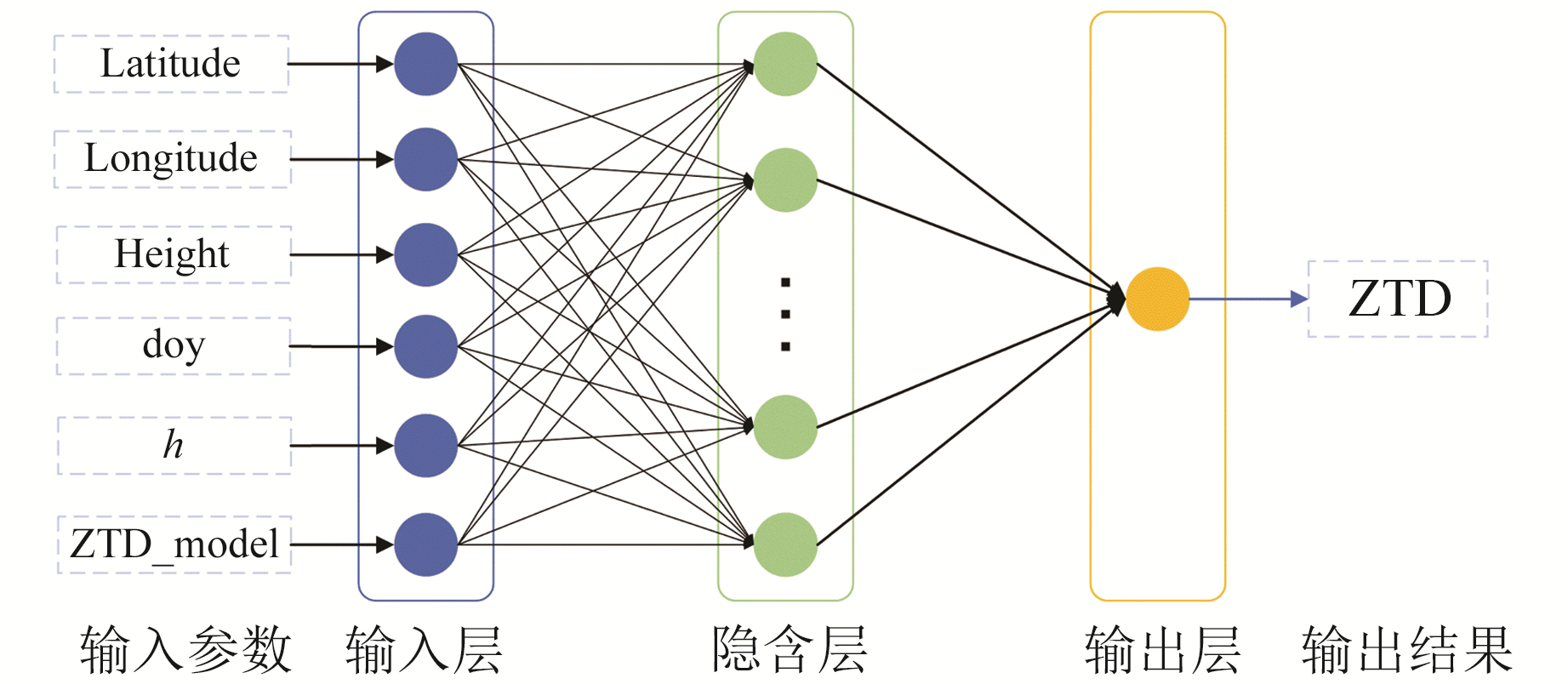
2.2 反向传播神经网络(BPNN)建模原理BPNN是一种按误差逆向传播算法训练的多层前馈网络[20],通过最小二乘准则使用梯度下降法来调整误差,减小网络输出值与目标值之间的差异,在诸多回归问题上得到广泛应用[21]。BPNN由输入层、隐藏层和输出层组成,其中输入层和输出层的神经元数量分别为自变量和因变量个数,模型结构如图 2所示。
|
图 2 BPNN结构原理 Fig. 2 BPNN structure principle |
BPNN模型中每一层神经元均通过激活函数直接连接到下一层神经元,本文采用双曲正切函数作为输入层与隐藏层之间的激活函数,采用线性函数作为隐藏层与输出层之间的激活函数。最终BPNN模型的输出可表示为:
| $Y(X)=g\left(\boldsymbol{W}_{3, 2} \cdot f\left(\boldsymbol{W}_{2, 1} \cdot X+\boldsymbol{b}_1\right)+\boldsymbol{b}_2\right)$ | (3) |
式中,X、Y为模型的输入和输出,W3, 2和W2, 1为权重矩阵,b1和b2为偏置矩阵,这4个矩阵存储BPNN模型的系数并通过反向传播算法进行优化。
3 模型精度分析十折交叉验证法可用来评估不同机器学习模型的性能[22]。将数据集随机且平均分成10组,其中9组作为训练集进行模型拟合,剩余1组作为测试集进行模型检验。由于每个样本均参与测试,十折交叉验证法具有十分可靠的模型精度评估效果。该检验过程需要重复10次,每运行完10次十折交叉验证算法后,计算并存储每个样本的残差,称之为交叉验证残差[19]。基于交叉验证残差,本文采用平均偏差(bias)和均方根误差(RMSE)作为模型的定量评价标准,bias能反映模型是否存在系统误差,RMSE则能反映预测值与真值之间的偏差,且对于数据中的异常值较为敏感,两者计算公式可表示为:
| $\operatorname{bias}=\frac{1}{N} \sum\limits_{i=1}^N\left({\rm{Z T D}}_i^{\text {pre }}-{\rm{Z T D}}_i^{\text {true }}\right)$ | (4) |
| $\mathrm{RMSE}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left({\rm{ZT D}}_i^{\mathrm{pre}}-\mathrm{ZTD}_i^{\mathrm{true}}\right)^2}$ | (5) |
式中,N为样本总数,ZTDipre为机器学习模型预测的ZTD值,ZTDitrue为GAMIT软件解算的ZTD_GAMIT。
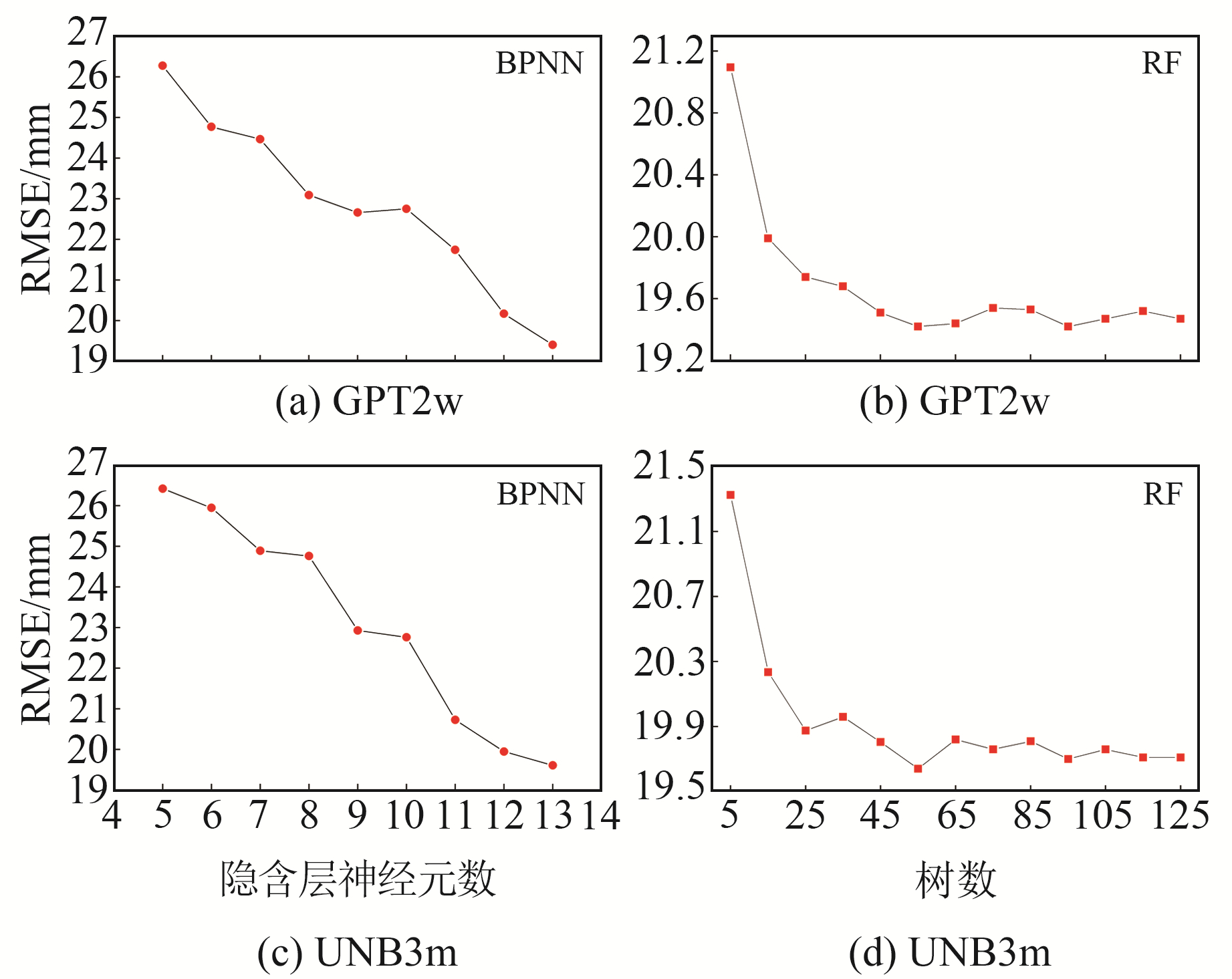
3.1 模型超参数确定实验过程中需要确定2种机器学习模型的最优超参数,即BPNN的隐含层神经元数和RF的回归树数。隐含层神经元数的确定目前无明确的方法,根据前人研究结果,隐含层的最佳神经元数可在
|
图 3 RMSE与树数、隐含层神经数的关系 Fig. 3 The relationship between RMSE and tree number and hidden layer neural number |
由图 3(a)和3(c)可知,随着隐含层神经元数的增加,基于2种背景数据的BPNN模型RMSE均减小,且都在神经元数为13时取得最小值。本文也对神经元数大于13的情况进行研究,发现RMSE虽然也在下降,但下降趋势明显减缓且需要花费很长时间进行训练,因此将BPNN的隐含层神经元数设为13。由图 3(b)和3(d)可知,随着RF模型树数的增加,基于2种背景数据的RF模型RMSE不断减小并趋于平缓,当回归树数量超过85以后,RMSE有所波动,但基本保持不变,因此将RF模型的回归树数设为85。
3.2 模型性能分析在确定超参数后,利用12个建模测站的2种背景数据等相关数据,基于十折交叉验证法分别对2种机器学习模型的拟合精度进行测试,即将建模测站的ZTD真值与拟合值进行对比,得到交叉验证残差值(bias),以分析2种模型的可靠程度。
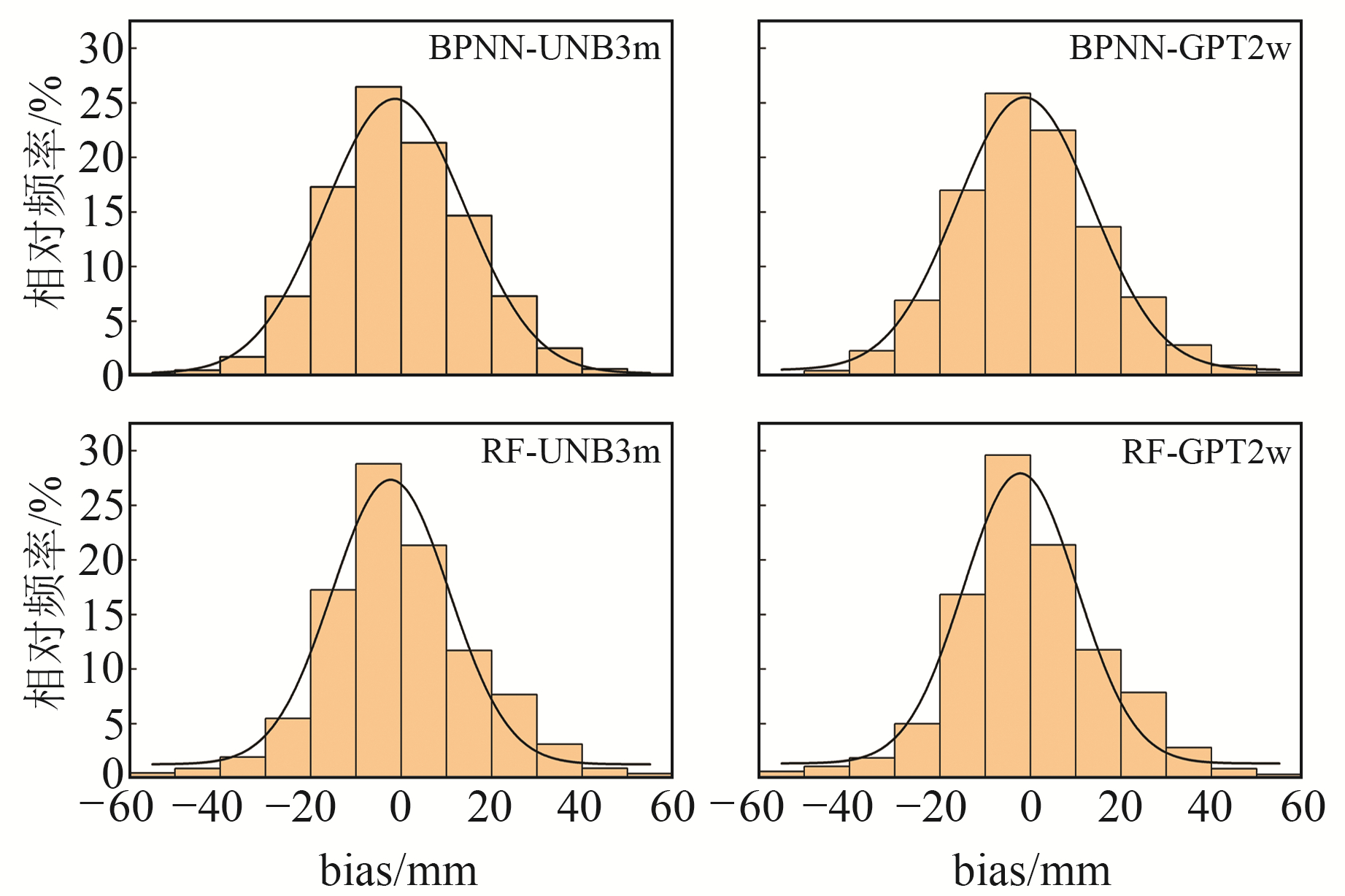
由图 4可知,2种模型的bias均近似服从正态分布,在[-20,20]分布区间内2种模型的相对频率均接近80%。但BPNN模型在[-60,-40]和[40, 60]区间的相对频率小于RF模型,说明BPNN模型的bias更加集中;BPNN模型的正负值分布也比RF模型更加均匀。上述分析表明,BPNN模型的拟合精度优于RF模型,并且以ZTD_UNB为输入参数的建模精度最好。为进一步分析2种模型的拟合精度,分别计算其bias和RMSE,结果见表 1(单位mm)。
|
图 4 基于不同背景数据的2种模型交叉验证残差值 Fig. 4 Cross-validation residual values of two models based on different background data |
|
|
表 1 2种模型的拟合精度 Tab. 1 Fitting accuracy of two models |
从整体上看,2种模型的bias均很小,说明在很大程度上消除了模型拟合的系统误差。以ZTD_UNB和ZTD_GPT为输入参数建立的2种模型的拟合精度结果表明,BPNN模型的拟合精度略高于RF模型,具有更好的拟合性能。
3.3 模型预测精度分析使用训练好的2种模型对CIT1测站31 d的ZTD值进行预测,以检验模型的预测精度。分别将每天24个真值和预测值计算平均值作为当天的真值和预测值,并以此计算2种模型每日的平均绝对偏差和RMSE误差,结果如图 5和图 6所示。
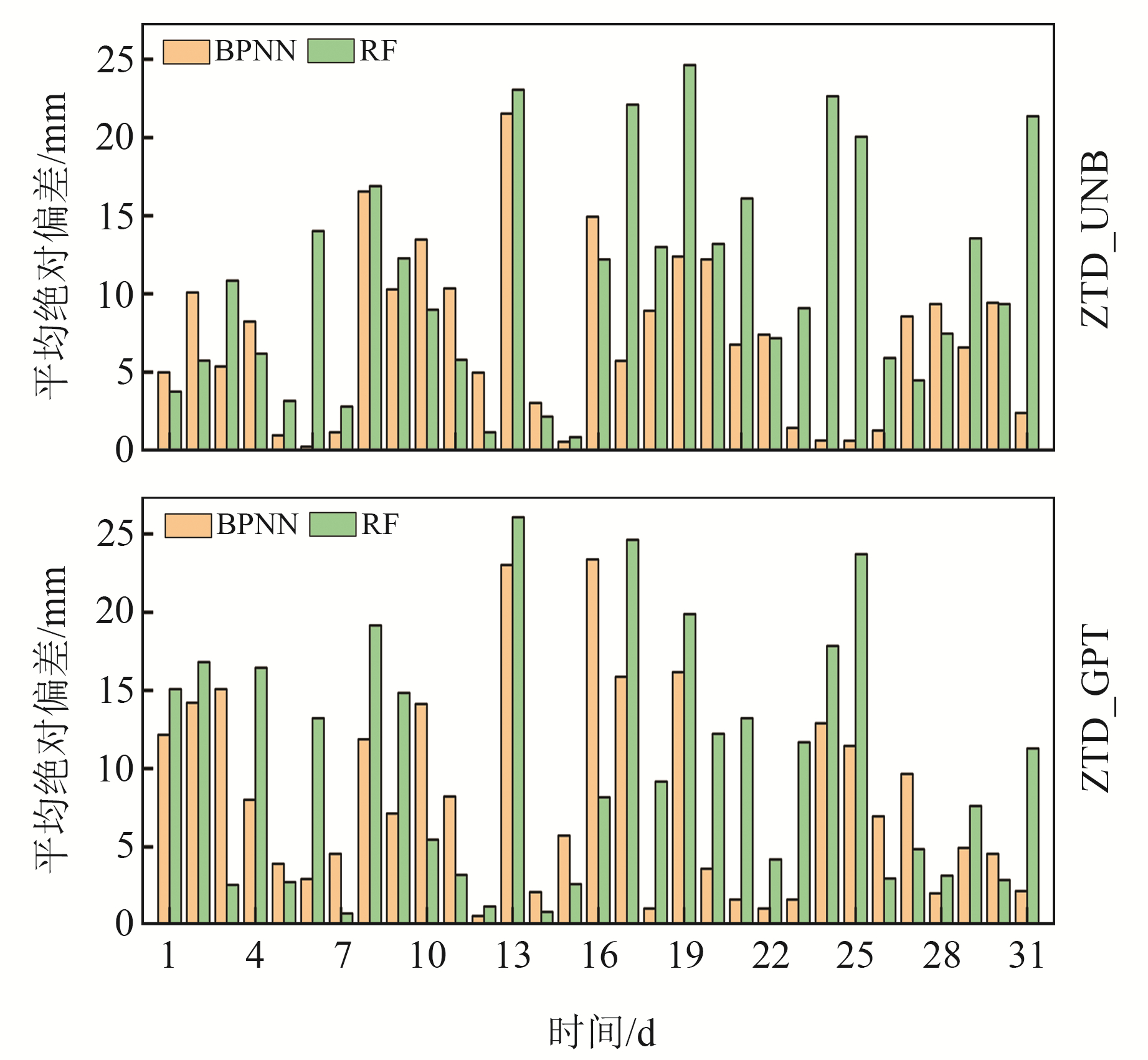
|
图 5 2种模型在CIT1测站的预测绝对偏差对比 Fig. 5 Comparison of the absolute deviation of two models in CIT1 station |
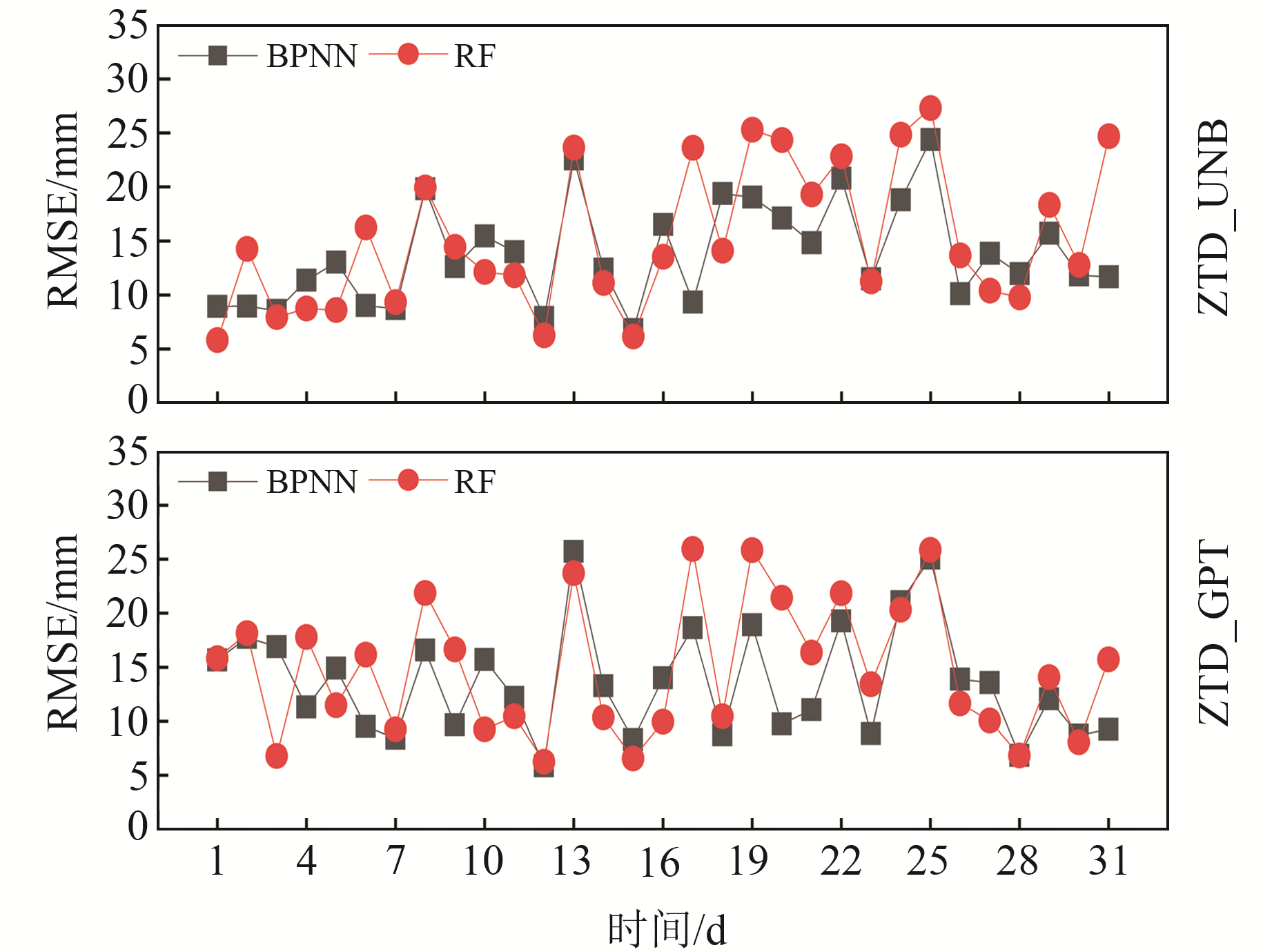
|
图 6 2种模型在CIT1测站的预测精度RMSE对比 Fig. 6 Comparison of the prediction accuracy RMSE of two models in CIT1 station |
由图 5可知,BPNN模型的预测残差总体上小于RF模型,说明BPNN模型的预测精度和整体稳定性更好。由图 6可知,2种模型预测值的RMSE基本都在20 mm以内,BPNN模型预测值的RMSE在15 mm上下波动,RF模型预测值的RMSE略差;BPNN模型整体上优于RF模型,并且具有更好的稳定性。
由表 2(单位mm)可知:1)2种模型在实际预测中均基本消除了系统误差,预测结果RMSE都在20 mm左右。BPNN模型预测ZTD值的RMSE小于RF模型,表明BPNN模型的预测精度优于RF模型。综合来看,以ZTD_UNB值为输入的BPNN模型预测效果最好,预测精度比以ZTD_GPT为输入的RF模型提高27%。但需要注意的是,由于BPNN模型的复杂度高于RF模型,在模型拟合阶段,BPNN模型所花费的时间要长于RF模型,随着数据量的增大时间差距也会逐渐增大。2)从改进模型来看,BPNN模型的预测精度优于RF模型;从输入参数来看,以UNB3m模型值为输入参数的预测结果优于以GPT2w模型值为输入参数的预测结果。
|
|
表 2 2种模型的预测精度 Tab. 2 The prediction accuracy of the two models |
对研究区分别利用UNB3m和GPT2w-5模型估计ZTD值,计算其bias和RMSE,结果见表 3(单位cm)。由表可知,2种经验模型预测的RMSE值相较于文献[14]得到的全球RMSE值均偏大,可能是因为本文研究区较小且选取的研究时段在夏季,ZTD变化幅度大,从而导致2种经验模型在研究区的预测精度比全球范围的预测精度差。将2种模型以ZTD_UNB和ZTD_GPT为输入参数得到的预测RMSE值求平均作为该模型的预测RMSE,求得BPNN模型的预测RMSE为15.23 mm,RF模型的预测RMSE为20.11 mm,相比于GPT2w-5模型的精度验证结果分别提高83.24%和77.87%,相比于UNB3m模型的精度验证结果分别提高78.73%和71.91%。
|
|
表 3 两种经验模型的预测精度 Tab. 3 The prediction accuracy of two empirical models |
本文首先介绍RF和BPNN两种机器学习算法的基本原理和模型精度,然后结合测站纬度、经度、大地高、年积日、每日小时数和背景数据构建2种区域ZTD改进模型,并讨论模型超参数的确定过程;最后在此基础上对RF和BPNN模型的拟合性能和预测精度进行对比分析。研究结果表明,2种改进模型的预测精度都在20 mm以内,相较于目前常用的GPT2w模型和UNB3m模型都有较大程度的提高;BPNN模型的预测精度优于RF模型,前者的预测RMSE比后者提高24.3%。与传统的经验ZTD模型相比,本文构造的模型结构相对简单,且无需进行大量数据准备,这对于经验ZTD模型精度优化、区域ZTD建模和较短时间内的GNSS水汽反演等具有重要意义。
本文仅对基于2种机器学习方法的区域ZTD改进模型进行研究,并对比分析两者的建模精度,但未涉及测站数目、测站地理位置分布、建模区域大小等相关因素对建模性能影响的研究,后续需开展进一步的研究、讨论和验证。
| [1] |
黄聪, 郭杭. 基于GPT3模型的ZTD及PWV反演精度分析[J]. 大地测量与地球动力学, 2022, 42(5): 489-493 (Huang Cong, Guo Hang. Accuracy Analysis of ZTD and Precipitable Water Vapor Inversion Based on GPT3 Model[J]. Journal of Geodesy and Geodynamics, 2022, 42(5): 489-493)
(  0) 0) |
| [2] |
刘江涛, 刘双童, 叶正真, 等. 一种区域精密天顶对流层延迟组合预报模型[J]. 大地测量与地球动力学, 2022, 42(9): 951-956 (Liu Jiangtao, Liu Shuangtong, Ye Zhengzhen, et al. A Regional Precise Zenith Tropospheric Delay Combined Prediction Model[J]. Journal of Geodesy and Geodynamics, 2022, 42(9): 951-956)
(  0) 0) |
| [3] |
童梦想, 於三大, 夏朋飞, 等. 顾及水汽衰减因子的中国区域大气可降水量模型的建立与分析[J]. 大地测量与地球动力学, 2022, 42(7): 745-749 (Tong Mengxiang, Yu Sanda, Xia Pengfei, et al. Analysis of Atmospheric Precipitable Water Vapor Model in China with Water Vapor Decrease Factor[J]. Journal of Geodesy and Geodynamics, 2022, 42(7): 745-749)
(  0) 0) |
| [4] |
Li H B, Wang X M, Wu S Q, et al. Development of an Improved Model for Prediction of Short-Term Heavy Precipitation Based on GNSS-Derived PWV[J]. Remote Sensing, 2020, 12(24)
(  0) 0) |
| [5] |
陈波波. 基于神经网络的GNSS区域大气延迟建模与精度分析[D]. 北京: 清华大学, 2020 (Chen Bobo. GNSS Regional Atmospheric Delay Modeling and Precision Analysis Based on Artificial Neural Network[D]. Beijing: Tsinghua University, 2020)
(  0) 0) |
| [6] |
Yang F, Guo J M, Zhang C Y, et al. A Regional Zenith Tropospheric Delay(ZTD) Model Based on GPT3 and ANN[J]. Remote Sensing, 2021, 13(5)
(  0) 0) |
| [7] |
谭勇, 姚宜斌. 常用对流层延迟修正模型的适用性分析及精化[J]. 测绘科学, 2022, 47(6): 15-20 (Tan Yong, Yao Yibin. Applicability Analysis and Refinement of Tropospheric Delay Correction Models[J]. Science of Surveying and Mapping, 2022, 47(6): 15-20)
(  0) 0) |
| [8] |
黄良珂, 陈华, 刘立龙, 等. 一种新的高精度全球对流层天顶延迟模型[J]. 地球物理学报, 2021, 64(3): 782-795 (Huang Liangke, Chen Hua, Liu Lilong, et al. A New High-Precision Global Model for Calculating Zenith Tropospheric Delay[J]. Chinese Journal of Geophysics, 2021, 64(3): 782-795)
(  0) 0) |
| [9] |
肖恭伟, 欧吉坤, 刘国林, 等. 基于改进的BP神经网络构建区域精密对流层延迟模型[J]. 地球物理学报, 2018, 61(8): 3 139-3 148 (Xiao Gongwei, Ou Jikun, Liu Guolin, et al. Construction of a Regional Precise Tropospheric Delay Model Based on Improved BP Neural Network[J]. Chinese Journal of Geophysics, 2018, 61(8): 3 139-3 148)
(  0) 0) |
| [10] |
杨旭, 何祥祥, 王媛媛, 等. 一种基于机器学习算法的区域/单站ZTD组合预测模型[J]. 全球定位系统, 2022, 47(1): 98-102 (Yang Xu, He Xiangxiang, Wang Yuanyuan, et al. A Regional/Single Station ZTD Combined Forecasting Model Based on Machine Learning Algorithm[J]. GNSS World of China, 2022, 47(1): 98-102)
(  0) 0) |
| [11] |
郭骐嘉, 姚宜斌, 周永江. 融合GNSS气象参数的PM2.5随机森林预测模型[J]. 测绘科学, 2021, 46(4): 37-42 (Guo Qijia, Yao Yibin, Zhou Yongjiang. PM2.5 Random Forest Prediction Model Incorporating GNSS Meteorological Parameters[J]. Science of Surveying and Mapping, 2021, 46(4): 37-42)
(  0) 0) |
| [12] |
李媛, 章浙涛, 何秀凤, 等. 雨雪天气对流层延迟改正模型适用性分析[J]. 导航定位学报, 2022, 10(2): 119-125 (Li Yuan, Zhang Zhetao, He Xiufeng, et al. Applicability Analysis of Tropospheric Delay Correction Model in Rain and Snow Weather[J]. Journal of Navigation and Positioning, 2022, 10(2): 119-125)
(  0) 0) |
| [13] |
黄东桂, 刘立龙, 黄良珂, 等. 桂林地区暴雨天气下两种对流层模型的适用性分析[J]. 桂林理工大学学报, 2022, 42(3): 672-678 (Huang Donggui, Liu Lilong, Huang Liangke, et al. Applicability Analysis of Two Tropospheric Models during Rainstorms in Guilin[J]. Journal of Guilin University of Technology, 2022, 42(3): 672-678)
(  0) 0) |
| [14] |
黄良珂. 顾及时空因素的高精度全球对流层关键参量模型构建研究[D]. 武汉: 武汉大学, 2020 (Huang Liangke. Development of the High-Precision Global Models for the Key Parameters of Troposphere Considering Spatiotemporal Factors[D]. Wuhan: Wuhan University, 2020)
(  0) 0) |
| [15] |
徐天河, 李耸, 王帅民, 等. 顾及气象数据的中国区域对流层延迟RBF神经网络优化模型[J]. 测绘学报, 2022, 51(8): 1 690-1 707 (Xu Tianhe, Li Song, Wang Shuaimin, et al. Improved Tropospheric Delay Model for China Using RBF Neural Network and Meteorological Data[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(8): 1 690-1 707)
(  0) 0) |
| [16] |
李耸. 基于机器学习的GNSS对流层延迟建模与预报[D]. 西安: 长安大学, 2021 (Li Song. Modeling and Predicting GNSS Tropospheric Delay Based on Machine Learning Algorithms[D]. Xi'an: Chang'an University, 2021)
(  0) 0) |
| [17] |
钟储汉, 李新瑞, 张双成, 等. GAMIT/TrackRT用于滑坡实时GNSS监测研究[J]. 测绘科学, 2022, 47(12): 57-65 (Zhong Chuhan, Li Xinrui, Zhang Shuangcheng, et al. GAMIT/TrackRT Used in Landslide Real-Time GNSS Monitoring[J]. Science of Surveying and Mapping, 2022, 47(12): 57-65)
(  0) 0) |
| [18] |
Breiman L. Random Forests[J]. Machine Learning, 2001, 45(1): 5-32
(  0) 0) |
| [19] |
杨丽萍, 苏志强, 侯成磊, 等. 基于随机森林的干旱区全极化SAR土壤含水量反演[J]. 吉林大学学报: 地球科学版, 2022, 52(4): 1 255-1 264 (Yang Liping, Su Zhiqiang, Hou Chenglei, et al. Soil Moisture Content Retrieval in Arid Area Based on Random Forest Using Polarimetric SAR Data[J]. Journal of Jilin University: Earth Science Edition, 2022, 52(4): 1 255-1 264)
(  0) 0) |
| [20] |
丁茂华, 胡伍生. 一种优化的基于神经网络的经验ZTD模型[J]. 测绘通报, 2017(1): 22-25 (Ding Maohua, Hu Wusheng. A Blind ZTD Model Based on Neural Network[J]. Bulletin of Surveying and Mapping, 2017(1): 22-25)
(  0) 0) |
| [21] |
Sun Z Y, Zhang B, Yao Y B. Improving the Estimation of Weighted Mean Temperature in China Using Machine Learning Methods[J]. Remote Sensing, 2021, 13(5)
(  0) 0) |
| [22] |
Rodríguez J D, Pérez A, Lozano J A. Sensitivity Analysis of k-Fold Cross Validation in Prediction Error Estimation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(3): 569-575
(  0) 0) |
2. Coal Industry Engineering Research Center of Mining Area Environmental and Disaster Cooperative Monitoring, Anhui University of Science and Technology, 168 Taifeng Street, Huainan 232001, China;
3. Key Laboratory of Aviation-Aerospace-Ground Cooperative Monitoring and Early Warning of Coal Mining-Induced Disasters of Anhui Higher Education Institutes, Anhui University of Science and Technology, 168 Taifeng Street, Huainan 232001, China
 2023, Vol. 43
2023, Vol. 43


