2. 63660部队,河南省洛阳市,471000;
3. 32016部队,兰州市,730020
精密单点定位技术(precise point positioning,PPP)是用户利用GNSS接收机的载波相位和测码伪距,使用高精度的轨道和钟差产品,通过模型改正等方式实现高精度定位的方法[1]。随着全球导航卫星系统(global navigation satellite system,GNSS)的发展,多系统组合数据处理能够有效利用现有星座资源,提升系统定位性能[2]。在多系统定位时,传统的处理各系统接收机方式为每个系统单独设置接收机钟差参数[3]。为更好地分析系统间特性,现在主要方法为选取一个接收机钟差基准,引入系统间偏差(inter-system bias,ISB)。许多学者对ISB的产生、特性以及相应的时变特性建模方法进行研究[4-6]。目前,ISB的时变特性模型主要有白噪声模型、随机游走模型和常数模型3种。Chen等[7-8]证明ISB与坐标参数无关,可以被钟差和模糊度参数吸收。Zhou等[9]基于不同分析中心发布的精密星历和钟差产品发现,多系统中ISB估计不仅取决于不同接收机的相关硬件延迟差异,还与钟差产品中不同GNSS间时间基准的差异相关。Liu等[10]发现ISB在1 d内具有稳定性,相邻日之间ISB的变化与MGEX时钟产品的基准变化有关。
2020-07北斗三号全球卫星导航系统(BDS-3)正式开通,并新增PPP-B2b精密单点定位服务(以下简称PPP-B2b)。该服务利用3颗地球同步轨道卫星通过B2b信号播发BDS-3和其他GNSS的轨道和钟差等改正信息,用户利用该服务可实现中国及周边区域的实时精密单点定位。研究发现,PPP-B2b服务播发的GPS卫星钟差时间基准存在多次变化的情况,因此在ISB时变模型选择时必须考虑该现象对ISB参数特性的影响。
本文详细介绍不同的ISB建模策略,分析PPP-B2b播发的GPS卫星钟差的时间基准在1 d内多次变化的现象,并通过MGEX测站数据进行静态和仿动态精密单点定位解算,分析不同的ISB时变特性建模策略对多系统组合实时定位性能的影响。
1 ISB建模在多系统PPP观测模型中,测站坐标、对流层延迟、接收机钟差、模糊度以及ISB五类参数为待估参数,参数估计采用Kalman滤波算法完成,通过逐历元读取观测文件仿实时条件处理。在Kalman滤波算法中,ISB参数中常用的历元间参数动力学模型主要有常数模型(CV)、随机游走模型(RW)和白噪声模型(WN),具体模型如下:
1) 随机游走模型,即保留上一个历元的估值ISBrC(k-1),并考虑ISB随时间变化的部分,该部分服从正态分布,即wk~N(0, σwk2),其中σwk2根据经验设置为1.7×10-7m2/s[11]。具体表达式为:
| $\operatorname{ISB}_r^C(k)=\operatorname{ISB}_r^C(k-1)+w_k$ | (1) |
式中,ISBrC(k)为第k个历元的ISB估值,wk为ISB参数对应的动态过程噪声。
2) 常数模型,即将ISB参数作为时间常数来估计。具体表达式为:
| $\operatorname{ISB}_r^C(k)=\operatorname{ISB}_r^C(k-1)$ | (2) |
3) 白噪声模型,即ISB参数被认为与时间无关,并在不同历元之间相互独立,在Kalman滤波中会赋予ISB过程噪声较大的方差,本文将σ2设置为109。具体表达式为:
| $\operatorname{ISB}_r^C(k) \sim N\left(0, \sigma^2\right)$ | (3) |
基于PPP-B2b服务的卫星钟差是经过广播星历钟差改正后得到,具体公式如下:
| $t_s=t_{\mathrm{brdc}}-C_0 / c$ | (4) |
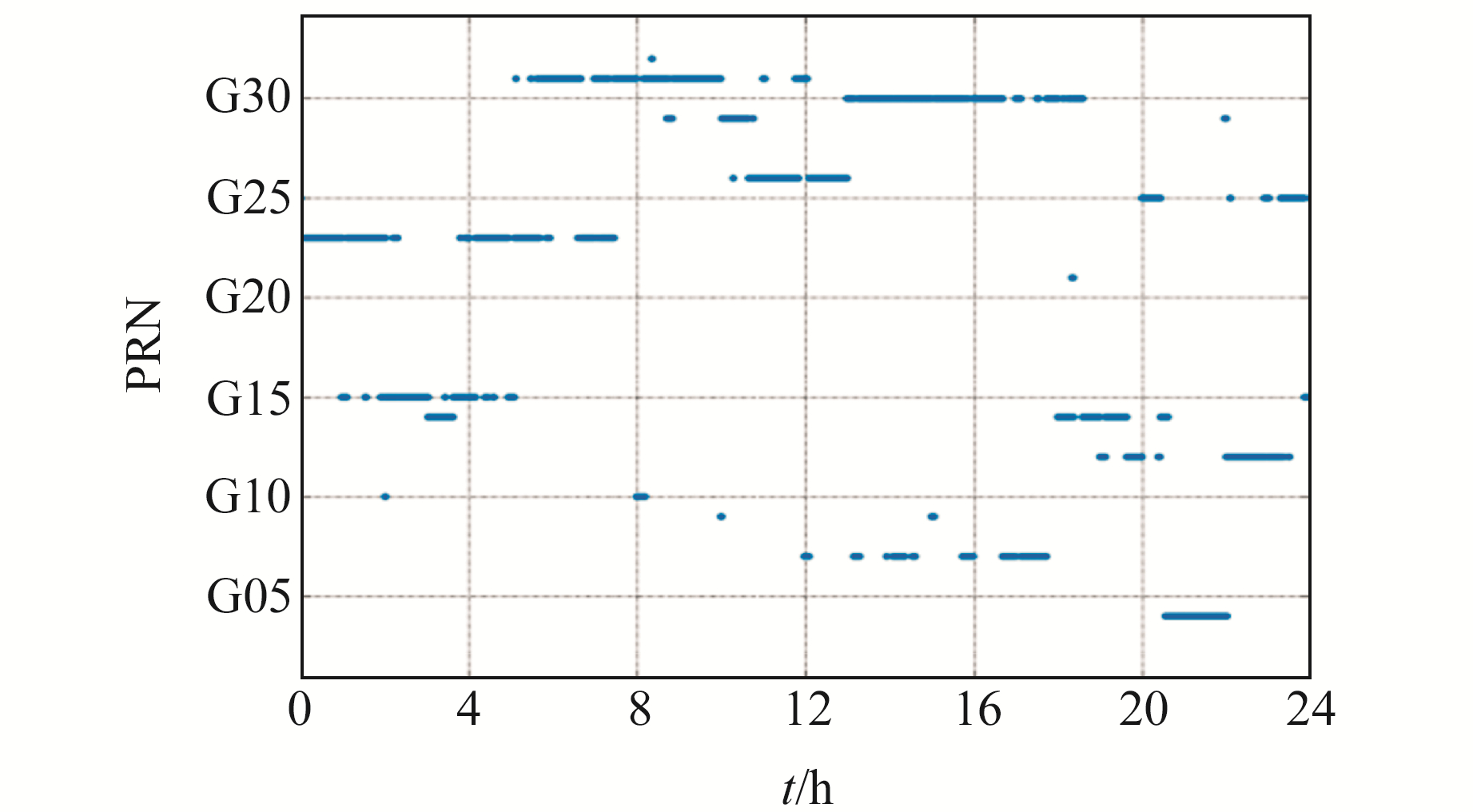
式中,ts为改正后的卫星钟差,tbrdc为广播星历的卫星钟差,C0为PPP-B2b电文中的钟差改正数,c为光速。在解码钟差改正数时发现,每个历元钟差改正数为0的卫星钟差就是通过广播星历计算得到的钟差。以2021-11-19经PPP-B2b钟差改正数恢复的钟差数据为例,图 1为该日钟差改正数为0的卫星PRN号。从图中可以看出,1 d之内钟差改正数为0的卫星发生多次变化。
|
图 1 钟差改正数为0的卫星PRN变化序列 Fig. 1 The PRN series of satellites with zero clock offset correction |
PPP-B2b采用分布在中国境内的跟踪站跟踪卫星进行观测,地面运控系统计算精密轨道钟差和差分码偏差生成快速星历参数,星历参数具有区域性、实时性等特点。一般实时卫星精密钟差ClkaS可以分为3个部分:
| $\mathrm{Clk}_a^S={O}_a+{O}_a^S+\mathrm{Clk}^S$ | (5) |
式中,S为卫星,a为分析中心,Oa为系统钟差时间基准,OaS为初始时钟偏差(初始卫星钟差与钟差真值差值),ClkS为相对卫星钟差[12]。其中卫星钟差解算中时间基准是所有卫星钟差参数的公共项,在多系统定位解算时,若单一系统的钟差时间基准在历元间发生较大变化,此项偏差会被ISB偏差参数吸收。因此,在实时PPP条件下,ISB模型的选择必须考虑系统钟差基准的变化。由式(5)可知,因OaS在连续弧段内为常数,且相对钟差在历元间的变化量级较小,可以通过钟差的历元间作差来反映时间基准在历元间的变化:
| $\nabla \mathrm{Clk}_a^S=\nabla O_a+\nabla \mathrm{Clk}^S$ | (6) |
国际GNSS服务(IGS)精密钟差产品处于同一时间基准,通过实时卫星精密钟差历元间差值减去IGS对应时刻钟差历元间差值,可以更好地反映时间基准历元间的变化情况:
| $\nabla O_a=\nabla \mathrm{Clk}_a^S-\nabla \mathrm{Clk}^S$ | (7) |
式中,
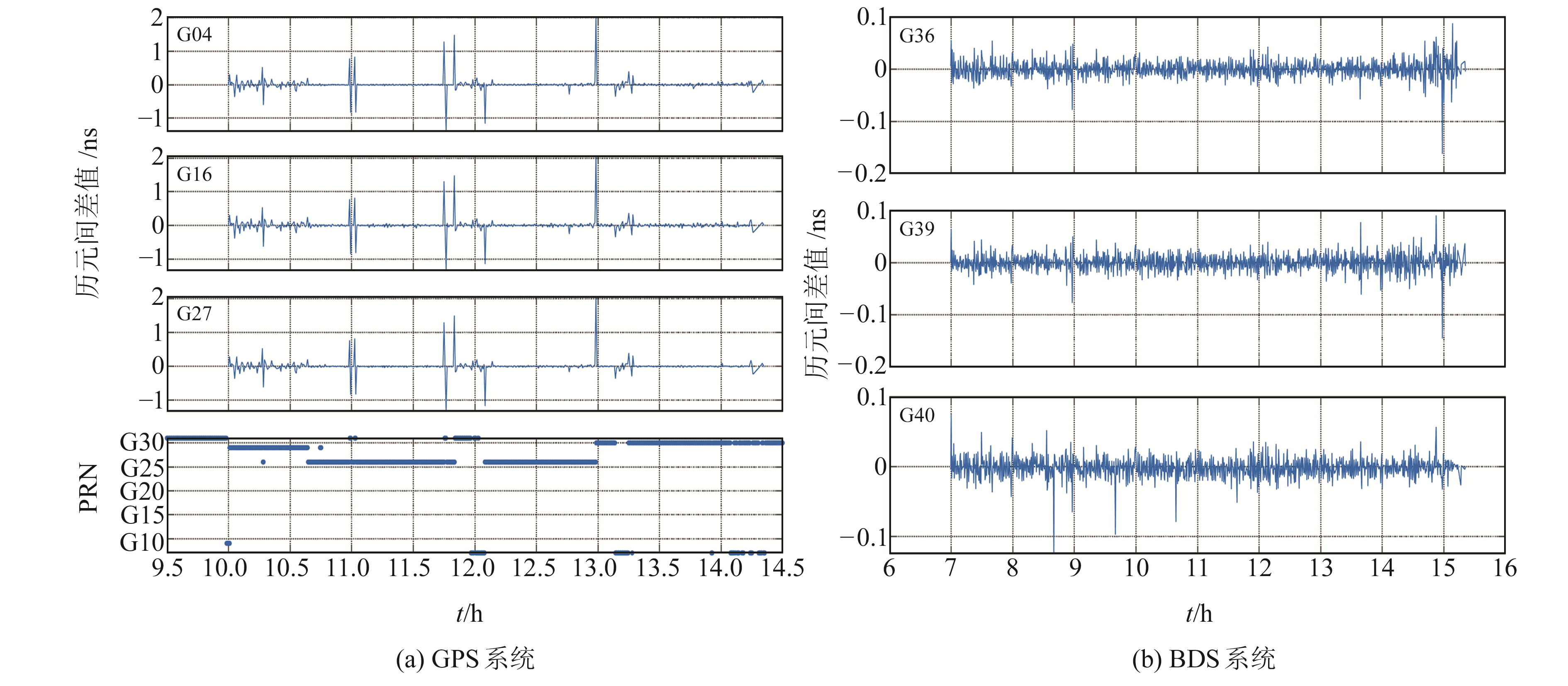
图 2为两个系统钟差历元间差值。图 2(a)为PPP-B2b钟差中G04、G16、G27三颗卫星钟差经式(7)计算得到的历元间差值以及对应时刻钟差改正数为0的卫星PRN变化序列图,可以看出,对于GPS系统,钟差时间基准发生变化会导致其他卫星的钟差差分序列发生较大跳变,且钟差为0的卫星切换时刻与卫星钟差基准变化时刻基本一致,因此可以将钟差改正数为0的卫星变化时刻作为卫星钟差时间基准变化时刻。图 2(b)为C36、C39、C40三颗卫星钟差历元间差分结果,可以看出,BDS系统卫星钟差历元间差分结果未发生较大量级的变化,且由图 1可知,BDS系统不存在钟差改正数为0的卫星,其实时钟差的时间基准未发生改变。因此,GPS与BDS两个系统卫星钟差的基准切换策略不同。
|
图 2 历元间钟差差值与钟差改正数为0的卫星PRN变化序列 Fig. 2 Clock offset difference between epochs and the PRN series of satellites with zero clock offset correction |
为评估不同ISB估计策略对PPP-B2b定位性能的影响,本文选取MGEX跟踪网中分布在亚太地区的JFNG、PTGG、USUD、URUM、GAMG五个测站2021-11-19~24观测数据,以白噪声模型、随机游走模型和常数模型分别作为ISB的时变模型,进行动静态实时定位解算实验,具体处理策略见表 1。
|
|
表 1 实验数据解算策略 Tab. 1 Processing strategy of experimental data |
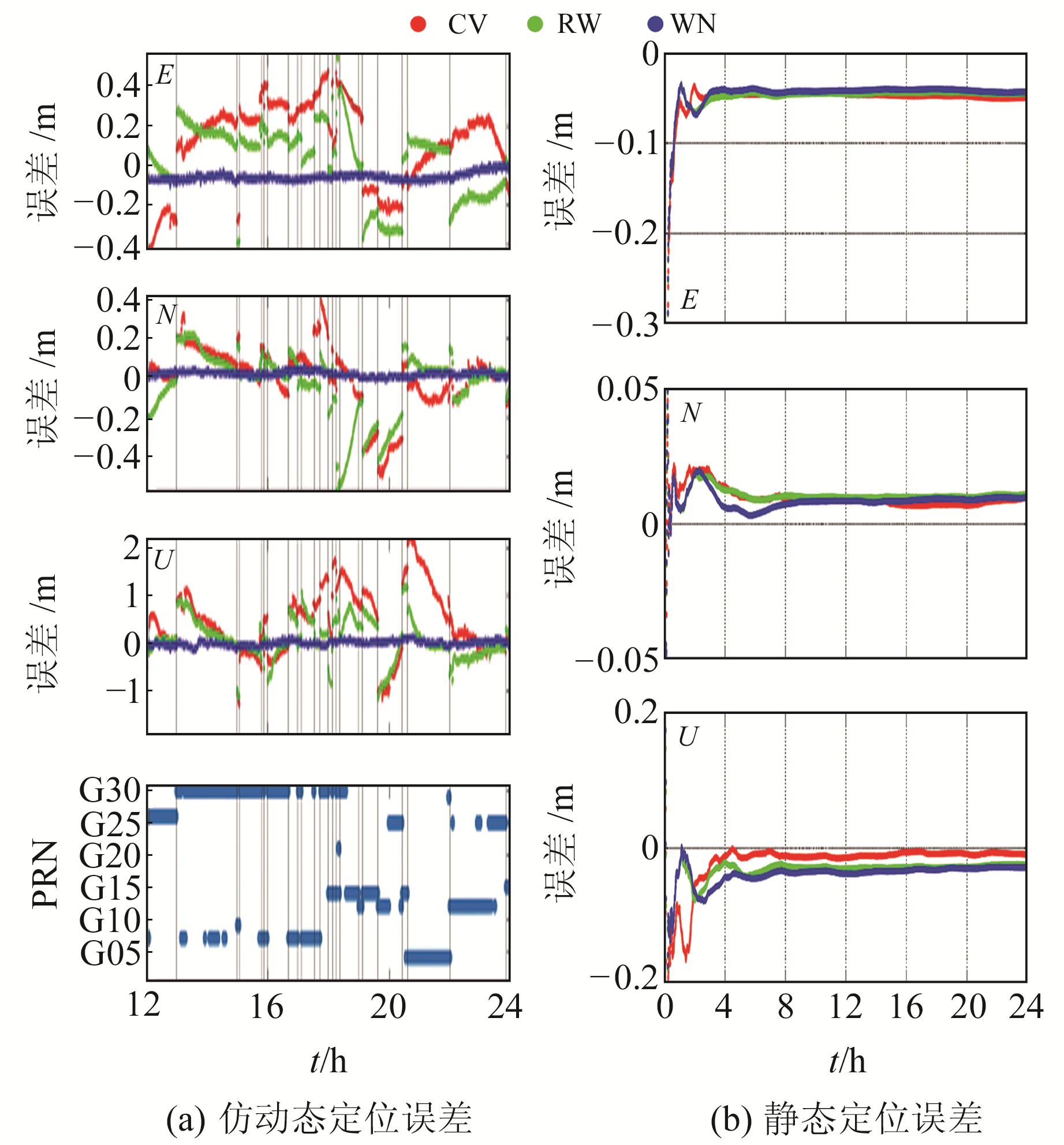
图 3为JFNG站2021-11-19基于PPP-B2b的GPS+BDS组合实时PPP误差时间序列以及相应时间段的卫星钟差时间基准变化。图 3(a)中竖线为CV和RW模型下定位结果出现明显跳变的时刻,可以看出,在仿动态模式下,ISB采用WN模型定位结果较好。当ISB采用CV和RW模型时定位曲线多次出现收敛后再次发生跳变的情况,会极大影响定位精度和稳定性。CV和RW两个模型的定位结果发生跳变时卫星钟差时间基准也会发生改变,说明在仿动态定位模式下,如果ISB参数采用CV和RW模型进行估计将无法完全吸收卫星钟差时间基准变化导致的ISB参数跳变,该部分偏差最终将被定位误差序列吸收。从图 3(b)可以看出,在静态定位模式下,CV、RW和WN三种模型收敛后各方向定位精度相当。
|
图 3 3种ISB模型实时PPP误差以及卫星钟差基准变化 Fig. 3 Real-time PPP errors of three different ISB models and satellite clock offset datum changes |
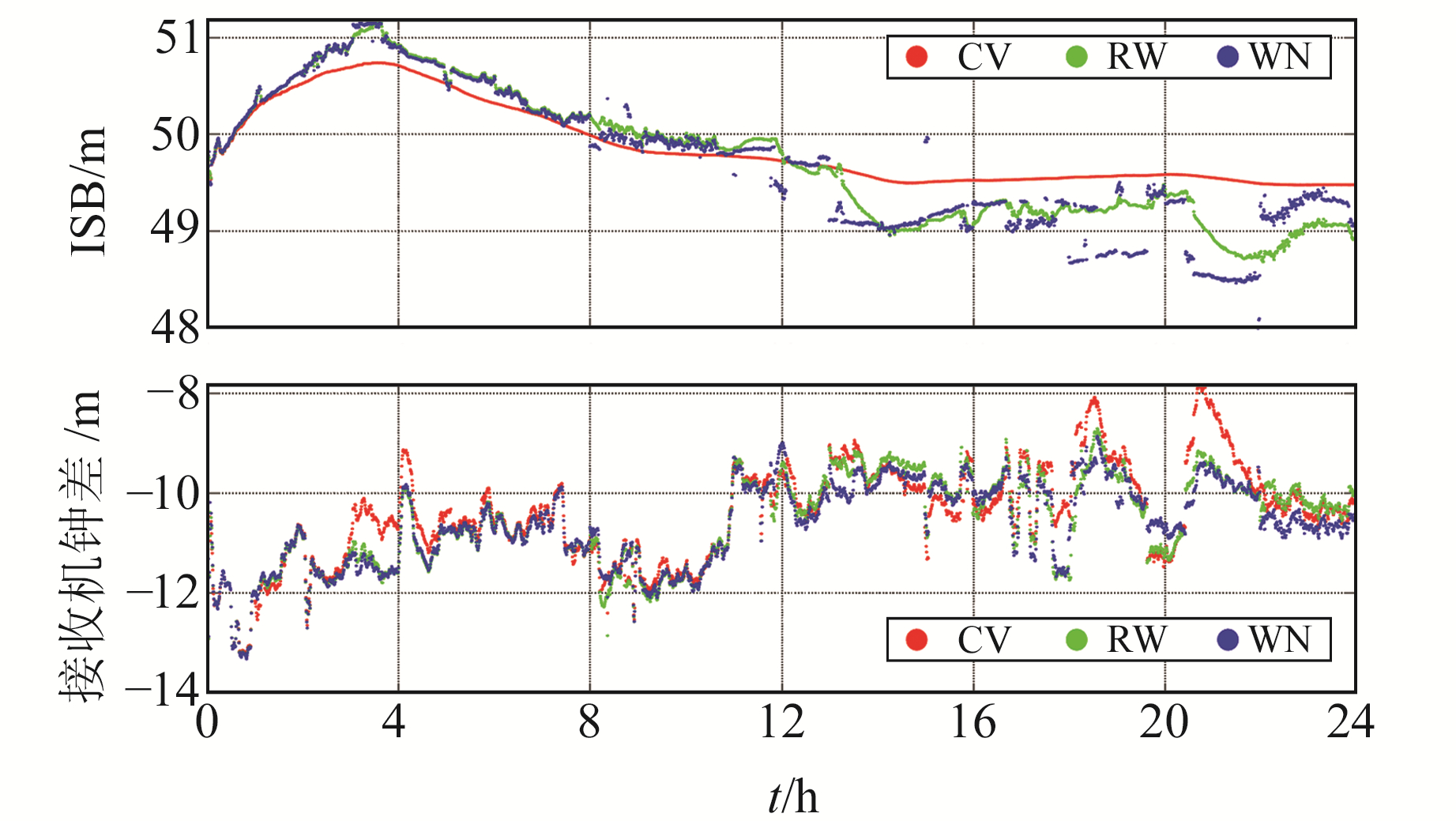
为进一步验证不同模型ISB估计结果的变化趋势,绘制JFNG站2021-11-19在动态定位条件下不同ISB模型的估值以及接收机钟差估值图(图 4)。由图可知,采用WN模型时ISB估值波动最为明显,且跳变时刻与钟差基准变化时刻基本吻合,说明在动态定位模式下,WN模型可充分吸收钟差基准变化的影响。反观接收机钟差估值,在卫星钟差基准变化时刻,CV模型的估计结果出现较大波动,WN模型波动幅度最小。对于CV和RW模型,由于无法对ISB变化进行有效建模,ISB模型误差不但会影响定位结果,同样也会对接收机钟差估计结果造成影响。
|
图 4 仿动态实时PPP下各种ISB估值与接收机钟差估值 Fig. 4 Estimation results of various ISB and receiver clock offset under simulated dynamic real-time PPP |
表 2为各测站在不同定位模式和ISB模型下6 d实时PPP定位精度。从表中可以看出,在动态定位模式下,相较于RW和CV模型,WN模型在E、N、U三个方向的定位精度有显著提升。WN模型在E、N、U三个方向的平均定位精度分别为5.4 cm、3.4 cm和11.2 cm,相较于CV模型在E方向上平均提高35.2 cm(提升约86.7%),N方向上平均提高28.0 cm(提升约89.2%),U方向上平均提高65.0 cm(提升约85.3%);在静态定位模式下,3种模型中WN模型定位精度最好,CV模型表现最差。相较于CV模型,WN模型在E方向上提升最为明显,约为27.7%。
|
|
表 2 各测站在3种ISB模型下实时PPP精度 Tab. 2 Real-time PPP accuracy of three ISB models for each station |
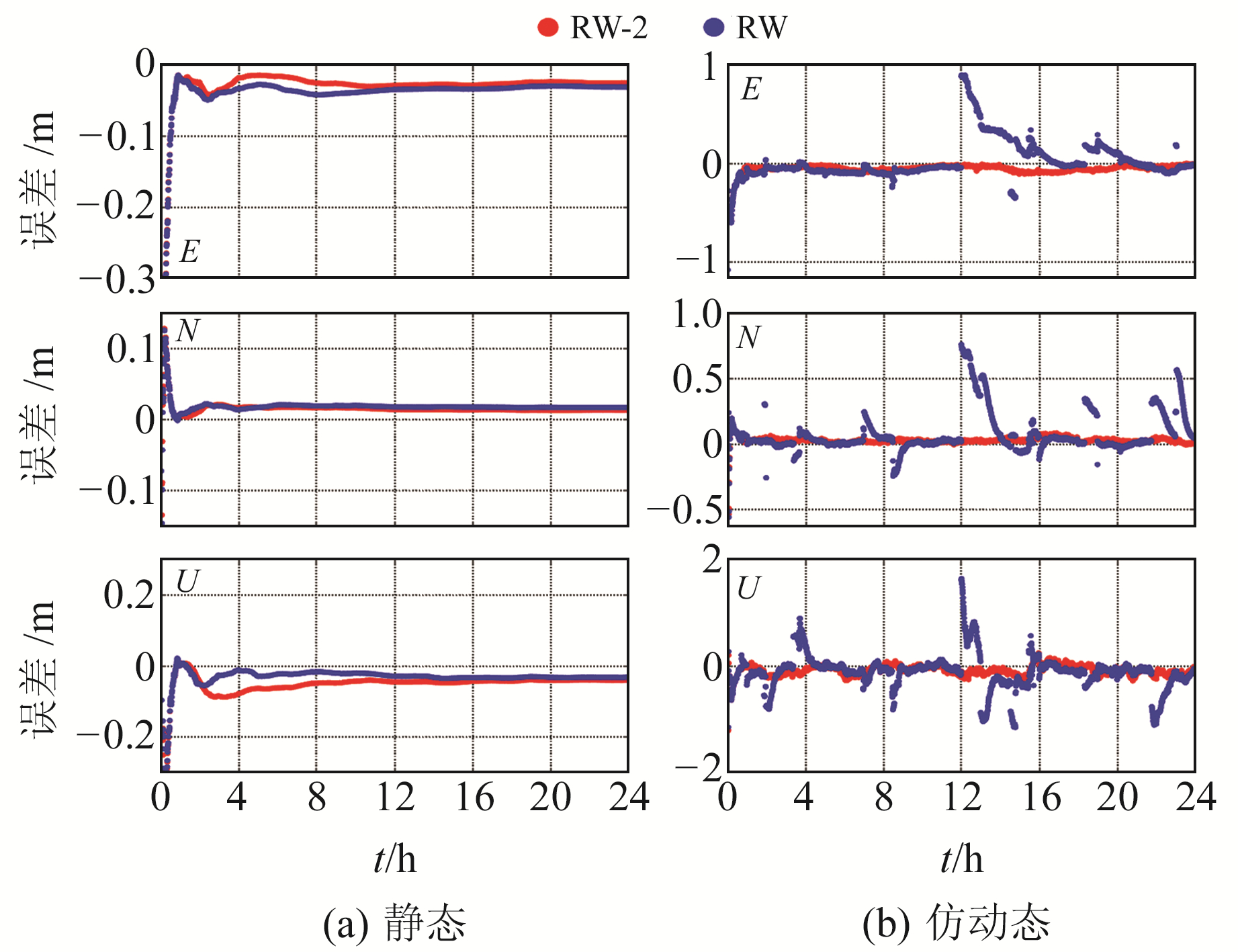
上述随机模型中过程噪声为常用经验值,为分析不同过程噪声取值的影响,同时考虑到GPS系统钟差时间基准变化量级达到ns级,因此将式(2)中过程噪声放大为1 ns,此方案记为RW-2。图 5为JFNG站动静态定位模式下随机游走模型采用不同过程噪声的误差序列。从图中可以看出,静态模式下收敛后两者定位精度相当;在动态模式下,考虑ns量级过程噪声的定位序列明显优于经验噪声。
|
图 5 不同过程噪声的RW模型误差序列 Fig. 5 Error series of RW model with different process noises |
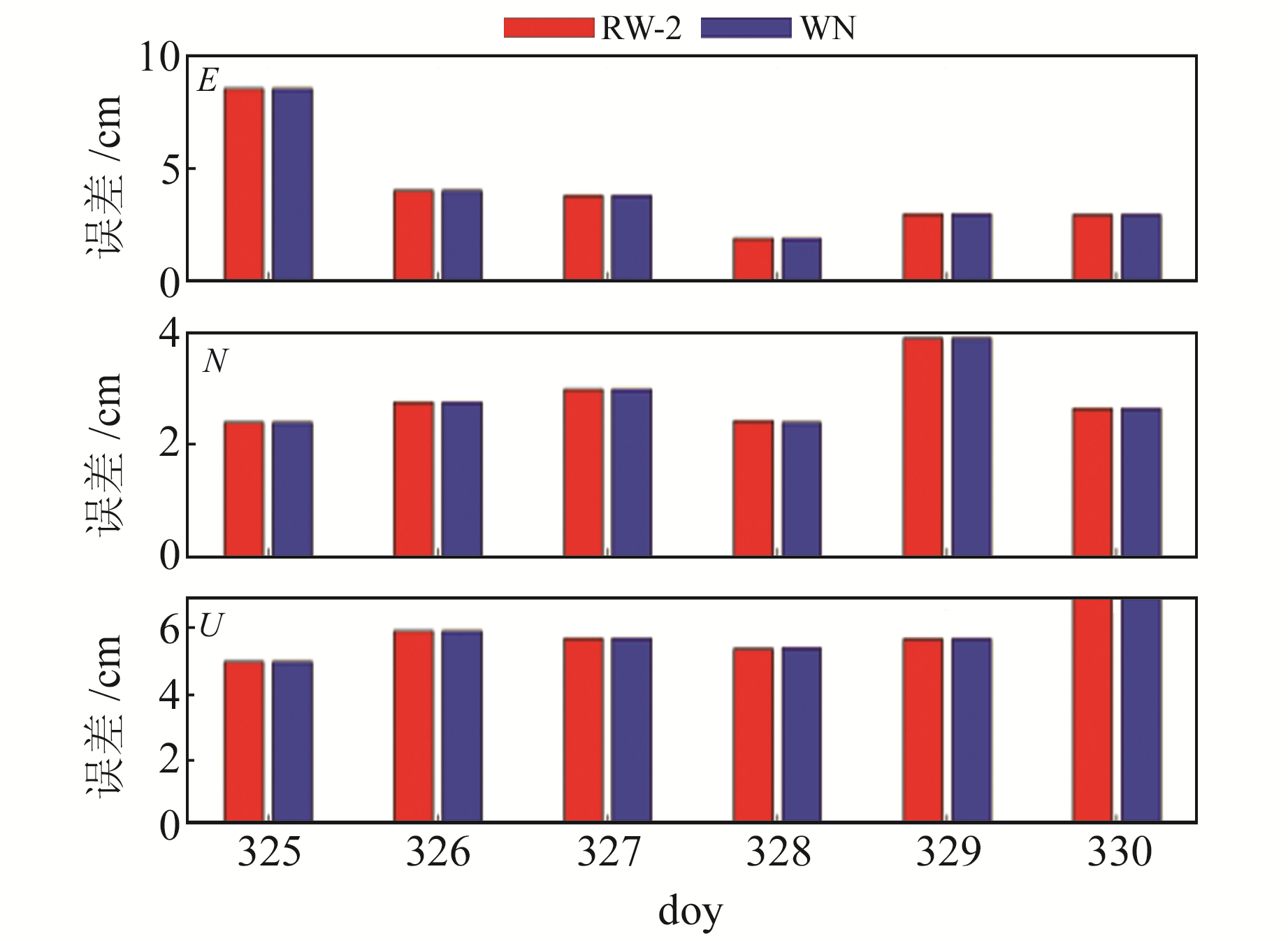
图 6为GAMG站基于白噪声模型和放大过程噪声的随机游走模型多天仿动态实时PPP定位结果对比。从图中可以看出,当随机游走模型设置合适的过程噪声后可以达到与白噪声模型近乎一样的定位效果。
|
图 6 WN模型和RW-2模型仿动态实时PPP精度对比 Fig. 6 Comparison of simulated dynamic real-time PPP accuracy between WN model and RW-2 model |
本文通过研究基于PPP-B2b服务的多系统组合实时定位性能发现,多系统组合时GPS卫星时间基准在1d内会发生多次变化,而BDS卫星时间基准不会改变,该项基准变化的差异会被ISB参数吸收。通过选取MGEX跟踪网中5个测站6 d的观测数据,以常数模型、随机游走模型和白噪声模型作为ISB参数的时变模型,进行动静态实时定位解算实验。结果表明,在静态模式下,ISB采用白噪声模型或随机游走模型的定位精度优于常数模型;在动态模式下,ISB采用白噪声模型较常数模型和设置经验值过程噪声的随机游走模型在定位性能上具有显著提升。在考虑实际过程噪声情况下,随机游走模型设置合适的过程噪声可以达到与白噪声模型相当的定位效果,较常数模型在E方向上提升约86.7%,N方向上提升约89.2%,U方向上提升约85.3%。
因此,对于PPP-B2b服务,多系统组合时ISB采用白噪声模型或设置合适噪声的随机游走模型可以有效吸收GPS卫星时间基准的变化,达到较好的定位效果。
| [1] |
Kouba J, Héroux P. Precise Point Positioning Using IGS Orbit and Clock Products[J]. GPS Solutions, 2001, 5(2): 12-28 DOI:10.1007/PL00012883
(  0) 0) |
| [2] |
祝会忠, 杨添宇, 赵洪涛, 等. GNSS多系统精密单点定位方法与性能分析[J]. 测绘科学, 2020, 45(12): 1-7 (Zhu Huizhong, Yang Tianyu, Zhao Hongtao, et al. GNSS Multi-System Precise Point Positioning Method and Performance Analysis[J]. Science of Surveying and Mapping, 2020, 45(12): 1-7)
(  0) 0) |
| [3] |
Lou Y D, Zheng F, Gu S F, et al. Multi-GNSS Precise Point Positioning with Raw Single-Frequency and Dual-Frequency Measurement Models[J]. GPS Solutions, 2016, 20(4): 849-862 DOI:10.1007/s10291-015-0495-8
(  0) 0) |
| [4] |
Bakker P F, Tiberius C C J M. Real-Time Multi-GNSS Single-Frequency Precise Point Positioning[J]. GPS Solutions, 2017, 21(4): 1 791-1 803 DOI:10.1007/s10291-017-0653-2
(  0) 0) |
| [5] |
Jiang N, Xu Y, Xu T H, et al. GPS/BDS Short-Term ISB Modelling and Prediction[J]. GPS Solutions, 2017, 21(1): 163-175 DOI:10.1007/s10291-015-0513-x
(  0) 0) |
| [6] |
El-Mowafy A, Deo M, Rizos C. On Biases in Precise Point Positioning with Multi-Constellation and Multi-Frequency GNSS Data[J]. Measurement Science and Technology, 2016, 27(3)
(  0) 0) |
| [7] |
Chen J P, Zhang Y Z, Wang J G, et al. A Simplified and Unified Model of Multi-GNSS Precise Point Positioning[J]. Advances in Space Research, 2015, 55(1): 125-134 DOI:10.1016/j.asr.2014.10.002
(  0) 0) |
| [8] |
Chen J P, Wang J G, Zhang Y Z, et al. Modeling and Assessment of GPS/BDS Combined Precise Point Positioning[J]. Sensors, 2016, 16(7)
(  0) 0) |
| [9] |
Zhou F, Dong D N, Li P, et al. Influence of Stochastic Modeling for Inter-System Biases on Multi-GNSS Undifferenced and Uncombined Precise Point Positioning[J]. GPS Solutions, 2019, 23(3)
(  0) 0) |
| [10] |
Liu T, Yuan Y B, Zhang B C, et al. Multi-GNSS Precise Point Positioning(MGPPP) Using Raw Observations[J]. Journal of Geodesy, 2017, 91(3): 253-268 DOI:10.1007/s00190-016-0960-3
(  0) 0) |
| [11] |
Li L Y, Lu Z P, Li J, et al. Parallel Resolution of Large GNSS Networks Using Carrier Ranges[J]. Advances in Space Research, 2020, 66(11): 2 621-2 628 DOI:10.1016/j.asr.2020.09.006
(  0) 0) |
| [12] |
Yao Y B, He Y D, Yi W T, et al. Method for Evaluating Real-Time GNSS Satellite Clock Offset Products[J]. GPS Solutions, 2017, 21(4): 1 417-1 425 DOI:10.1007/s10291-017-0619-4
(  0) 0) |
2. 63660 Troops of PLA, Luoyang 471000, China;
3. 32016 Troops of PLA, Lanzhou 730020, China
 2023, Vol. 43
2023, Vol. 43

