随着人类社会的进步和科技的迅速发展,以GNSS/INS组合导航为代表的导航定位技术在人类社会、经济和军事活动中发挥着越来越重要的支撑作用[1]。然而,受制于城市复杂环境,GNSS信号易受干扰,导致GNSS定位精度严重劣化甚至定位失败;受限于低成本MEMS IMU(micro-electro mechanical system inertial measurement unit)的自身缺陷,当缺乏外部观测约束时,SINS(strapdown inertial navigation system)误差随时间迅速累积。
面对动态信息和观测信息质量差的问题,许多学者提出抗差自适应滤波方法。Sage-Husa抗差算法通过开窗求历元间均值的方法构造抗差因子以削弱异常观测的影响[2-5],但该方法未考虑历元间新息不满足同分布的情况,会影响抗差因子的准确性。Guo等[6]设计一种基于卡方检验的判断指标检测观测异常,并构造多抗差因子进行抗差,但该抗差方法仅限于单个历元中对不同元素进行抗差,未考虑不同历元间的关系,自适应滤波在动态模型出现粗差时通过构造自适应因子对动态模型进行降权;Yang等[7]根据预设的动力学模型与实际载体运动不符值设计自适应滤波;赵方等[8]对自适应辅助更新算法、过程噪声协方差矩阵自适应估计算法等展开研究;周彬等[9]通过状态不符值构造自适应因子控制动态模型权重。上述方法均未对误差模型作出决策判断,在复杂场景下未针对误差模型进行决策而使用抗差或者自适应可能会导致定位精度出现劣化。
合理的决策算法与抗差算法和自适应算法同等重要,观测模型异常和动态模型异常需要依靠决策算法进行鉴别。Yang等[10]利用车辆的非完整性约束(NHC)进行抗差自适应决策,即利用车辆自身侧向、纵向速度为零的特性判断动态模型是否出现异常,但该算法无法在进行NHC决策的同时进行NHC更新,而在复杂环境中NHC更新可显著提升车载导航定位精度,因此舍弃NHC更新并不可取。高怡等[11]基于状态相关因子构造状态相关系统,并通过等价权矩阵进行抗差自适应滤波,然而该方法的抗差自适应因子均是通过新息构造,新息异常时无法判断具体是动态模型还是观测模型出现问题。
在GNSS/INS松组合基础上,构建一套以GNSS定位状态进行分类的改进双窗口Sage-Husa抗差算法,自适应算法采用传统新息自适应滤波,并通过改进的异常新息占比决策算法鉴别组合导航中可能出现的观测模型异常或动态模型异常,进而在抗差算法与自适应算法之间作出合理选择;最后通过实际路测实验对改进的抗差算法和决策算法的性能加以分析。
1 GNSS/INS松组合系统模型选取离散状态卡尔曼滤波作为最优估计算法,系统状态向量选择INS的15维误差状态:
| $\delta \boldsymbol{X}=\left[\begin{array}{lllll} \delta \boldsymbol{r}^c & \delta \boldsymbol{v}^c & \boldsymbol{\psi} & \boldsymbol{b}_g & \boldsymbol{b}_a \end{array}\right]^{\mathrm{T}}$ | (1) |
式中,δrc为惯导位置误差,δvc为速度误差,ψ为姿态误差,bg为陀螺仪零偏,ba为加速度计零偏。姿态误差建模为计算坐标系c系到平台坐标系p系的失准角ψ角误差模型。
将INS得到的一步预测位置与GNSS得到的观测位置之间的差值作为观测向量,同时考虑到分体式系统存在杆臂效应,需对其进行补偿。估计量与观测量作差可得卡尔曼滤波观测值:
| $\begin{gathered} \delta \boldsymbol{z}_r=\boldsymbol{D}_R\left(\hat{\boldsymbol{r}}_{\mathrm{GNSS}}^n-\tilde{\boldsymbol{r}}_{\mathrm{GNSS}}^n\right) \approx \\ \delta \boldsymbol{r}_{\mathrm{IMU}}^c+\left(\left(\boldsymbol{C}_b^n \boldsymbol{l}^b\right) \times\right) \boldsymbol{\psi}-\boldsymbol{e}_r \end{gathered}$ | (2) |
式中,DR为纬经高分量差异到北东地分量差异的转换矩阵,δrIMUc为惯导位置误差,Cbn为载体坐标系b系到导航坐标系n系的姿态转换矩阵,lb为b系下GNSS天线到IMU的杆臂向量,er为观测误差向量。位置更新设计矩阵H阵为:
| $\boldsymbol{H}=\left[\begin{array}{lllll} \boldsymbol{I}_{3 \times 3} & {\bf 0}_{3 \times 3} & \left(\left(\boldsymbol{C}_b^n \boldsymbol{l}^b\right) \times\right) & {\bf 0}_{3 \times 3} & {\bf 0}_{3 \times 3} \end{array}\right]$ | (3) |
抗差滤波通过构造抗差因子放大观测向量协方差矩阵以削弱异常观测模型的影响。传统Sage-Husa抗差算法由于利用单窗口而无法对不同分布的解状态新息向量加以区分,抗差因子构造会出现异常,从而无法准确反映当前历元观测模型的偏差。本文提出一种改进的双窗口Sage-Husa抗差模型,针对浮点解和固定解分别建立一个新息协方差窗口,并根据当前的解状态在不同窗口内计算抗差因子,以降低单窗口中不同分布新息带来的影响。
选取两个窗口分别保存N个历元的固定解或浮点解的新息协方差矩阵估计值,根据窗口内新息协方差矩阵的估计值和当前时刻新息协方差矩阵的理论值计算观测向量协方差矩阵的估计值,与先验的观测协方差阵Rk构造抗差因子λ,并用λ放大Rk。
| $\lambda=\frac{\operatorname{tr}\left(\frac{1}{N} \sum\limits_{i=0}^N \overline{\boldsymbol{V}}_{k-i} \overline{\boldsymbol{V}}_{k-i}^{\mathrm{T}}-\boldsymbol{H}_k \boldsymbol{P}_{k, k-1} \boldsymbol{H}_k^{\mathrm{T}}\right)}{\operatorname{tr}\left(\boldsymbol{R}_k\right)}$ | (4) |
| $\lambda=\max (\lambda, 1)$ | (5) |
式中,tr(·)为矩阵求迹运算,max(·)为求最大值运算,Hk为当前历元设计矩阵,Pk, k-1为一步预测状态协方差矩阵,Rk为量测噪声方差阵,Vk为一步预测值与观测值之间的差异即新息向量。量测噪声协方差矩阵经过抗差因子放大后变为:
| $\overline{\boldsymbol{R}}_k=\lambda \boldsymbol{R}_k$ | (6) |
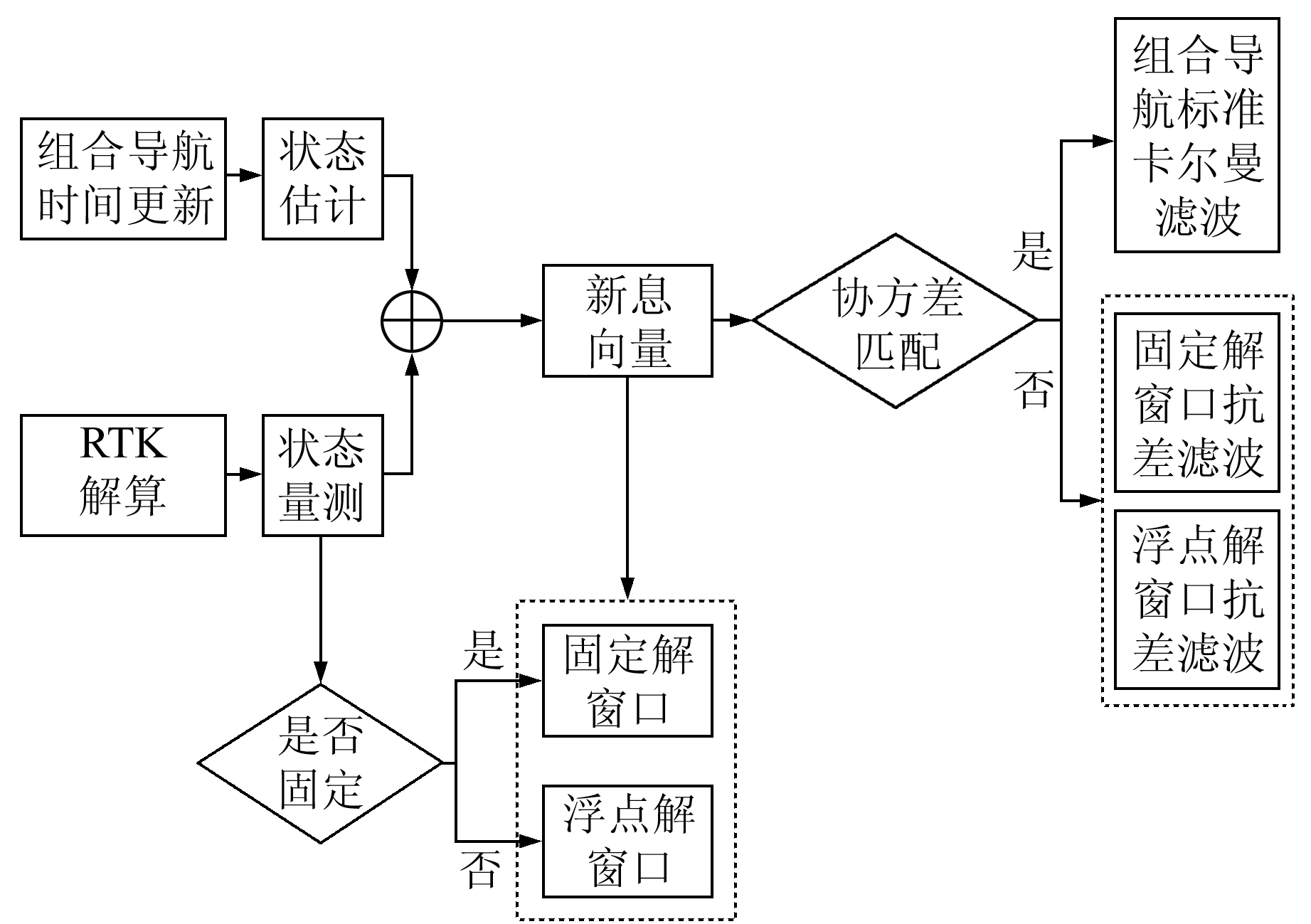
改进的双窗口Sage-Husa抗差算法结构如图 1所示,通过判断RTK解状态选择将新息协方差保存至固定解窗口或浮点解窗口,若组合导航量测更新时新息向量不匹配则根据当前时刻解状态选择对应窗口构造抗差因子来放大观测协方差阵,否则只进行标准卡尔曼滤波。
|
图 1 双窗口Sage-Husa抗差算法结构 Fig. 1 Structure of double-windows Sage-Husa robust algorithm |
抗差滤波和自适应滤波分别用于观测模型异常和动态模型异常,引入抗差自适应决策算法对异常情况加以识别有助于提升抗差自适应算法的准确性。抗差滤波选择前文中改进的双窗口Sage-Husa抗差滤波,自适应滤波选择传统的新息自适应滤波[12],决策模型选用改进的异常新息占比决策模型。
传统异常新息占比决策算法是将INS机械编排位置传入RTK解算的初始流动站位置,INS动态模型异常会导致滤波器异常新息占比偏高,可根据RTK解算中异常新息占比来决定进行抗差或自适应滤波。其中存在两个问题:一是判断新息是否异常的阈值未考虑新息向量中存在伪距和载波相位两种不同分布的观测;二是异常新息占比的阈值未考虑观测数的影响,观测数较多时应缩小占比阈值而偏向于自适应滤波,反之应增大阈值而偏向于抗差滤波。
针对第一个问题,对不同类型异常新息的阈值加以区分:
| $\left\{\begin{array}{l} \left|\tilde{V}_{i, p}\right|=\left|\frac{V_{i, p}}{\sigma_{v_{i, p}}}\right| \leqslant c_1 \\ \left|\tilde{V}_{j, \varphi}\right|=\left|\frac{V_{j, \varphi}}{\sigma_{v_{j, \varphi}}}\right| \leqslant c_2 \end{array}\right.$ | (7) |
式中,
针对第二个问题,根据RTK解算过程中的观测数量构建异常新息占比阈值的线性模型:
| $c=1-\frac{n v}{50}$ | (8) |
式中,c为异常新息占比阈值,nv为RTK观测值数量。该模型可以基本反映异常新息占比阈值随观测数量的增大而减小,能够更好地适应复杂环境下观测量波动较大的情况。
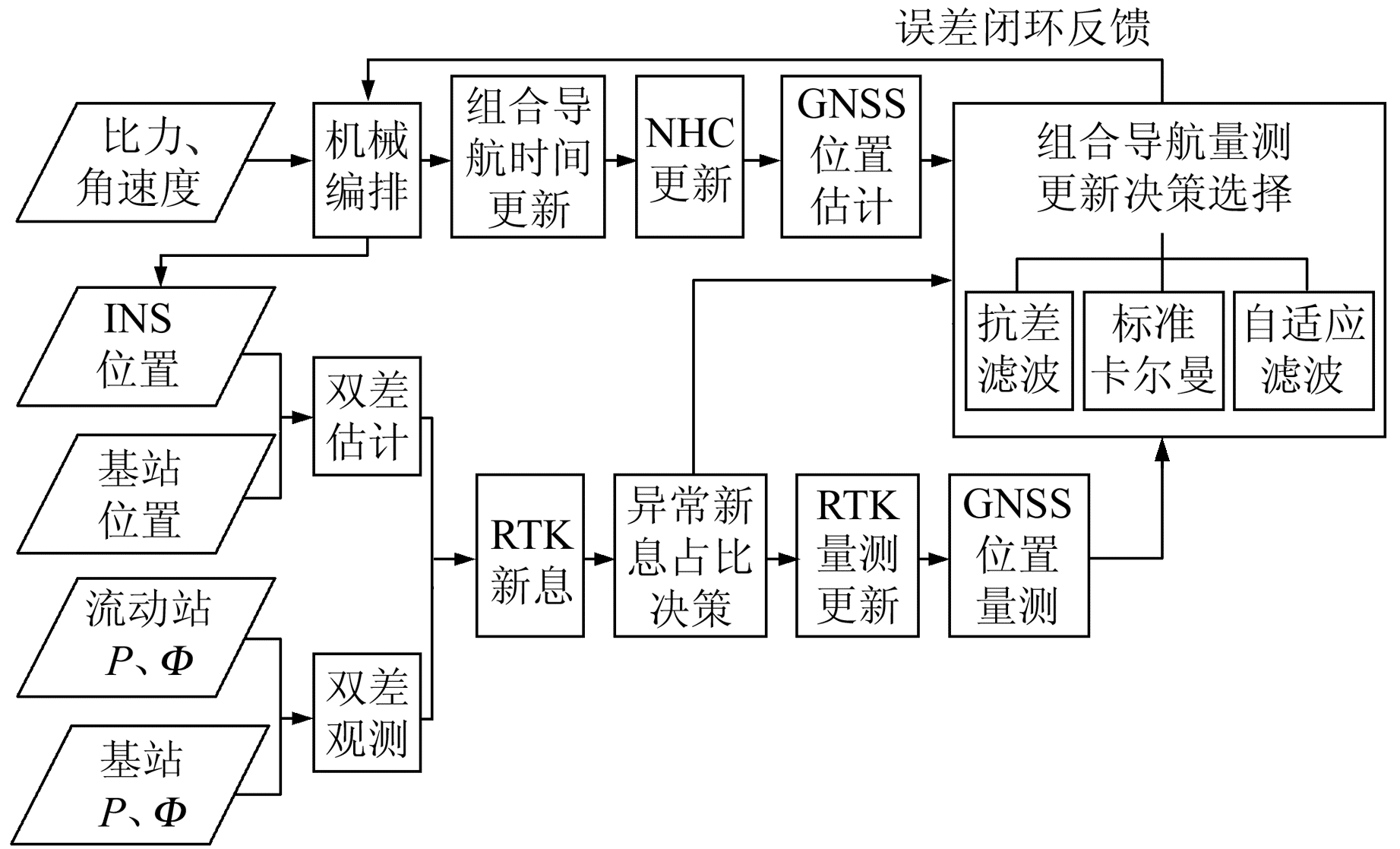
2.3 改进抗差自适应算法流程所构建的抗差自适应模型以及改进决策模型在松组合系统中的整体框架如图 2所示。
|
图 2 抗差自适应算法决策模型 Fig. 2 Decision model of robust and adaptive algorithm |
松组合动态模型机械编排后将INS位置传入量测模型的RTK双差观测值计算中(将INS位置状态协方差阵设置较大使INS对RTK解算几乎不产生影响,从而避免结果的相关性问题),计算异常新息所占比例,确定选择抗差或自适应滤波,滤波结束后将位置、速度、姿态的偏移量进行闭环反馈,校正INS误差。
3 实验论证与结果分析为评估所构建的改进自适应抗差算法的性能,对2021年在武汉市城区复杂环境下采集的一组车载GNSS+INS实测数据进行处理分析(待测数据由武汉迈普时空M39采集,参考真值由NovAtel公司SPAN-CPT6采集,两款设备的IMU参数如表 1所示)。
|
|
表 1 组合导航设备IMU参数 Tab. 1 IMU parameters of integrated navigation equipment |
实验分为两组进行分析,分别对应改进的双窗口Sage-Husa抗差滤波算法和改进的异常新息占比决策算法在自适应抗差滤波中的性能。实验场景选为林荫道及城市峡谷的复杂城区环境,轨迹和场景如图 3所示。

|
图 3 实验路线及场景 Fig. 3 The trajectory and scene of experiment |
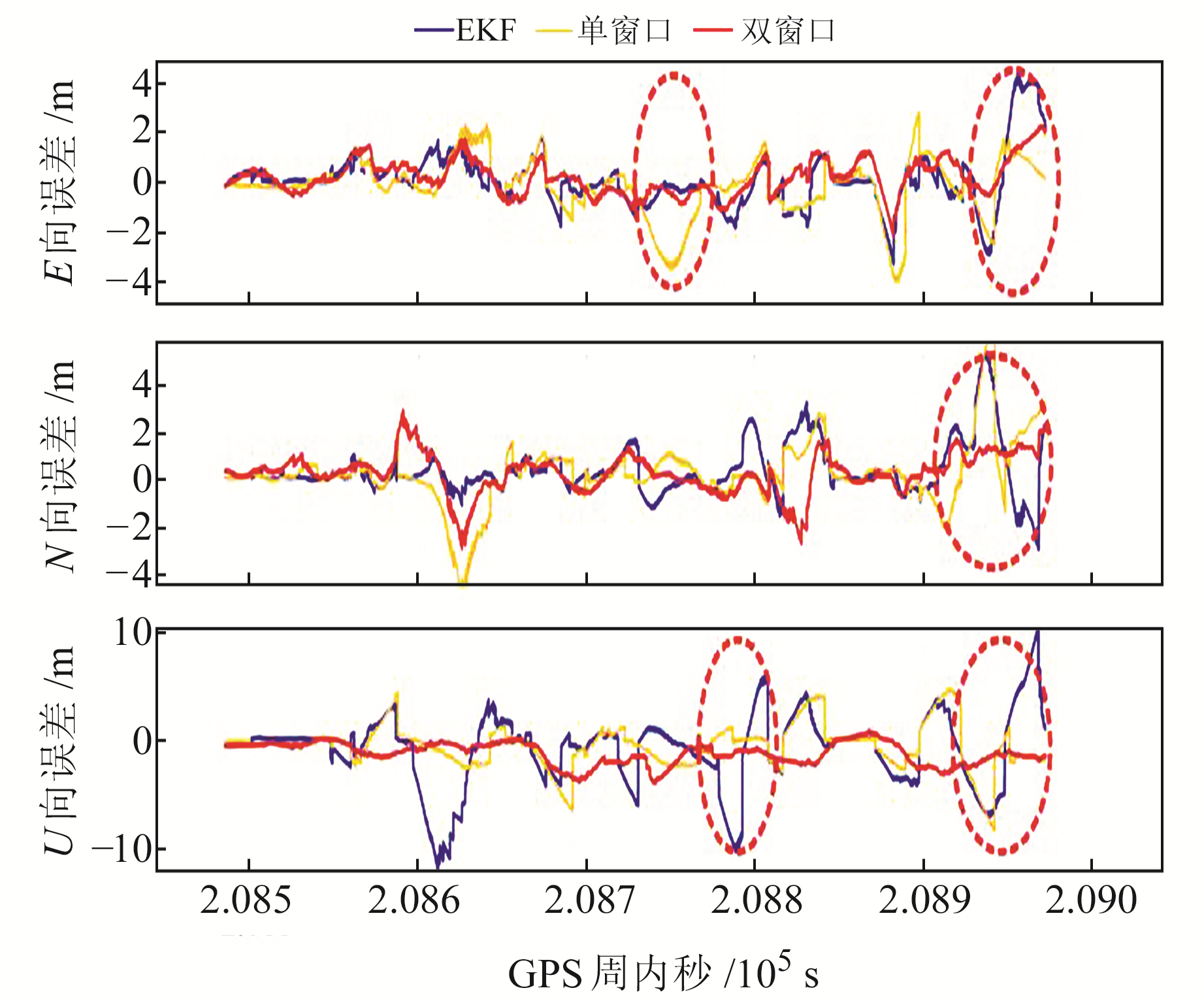
图 4为双窗口Sage-Husa抗差算法对比EKF和单窗口Sage-Husa抗差算法的位置误差,图中圆圈区域为改进算法提升明显的区域。双窗口Sage-Husa抗差算法性能整体明显优于EKF,在传统Sage-Husa抗差因子出现错误时,双窗口Sage-Husa抗差依然能保持较好的性能,尤其在天向方向位置精度提升效果更为明显。
|
图 4 抗差算法位置误差 Fig. 4 Position error of robust algorithm |
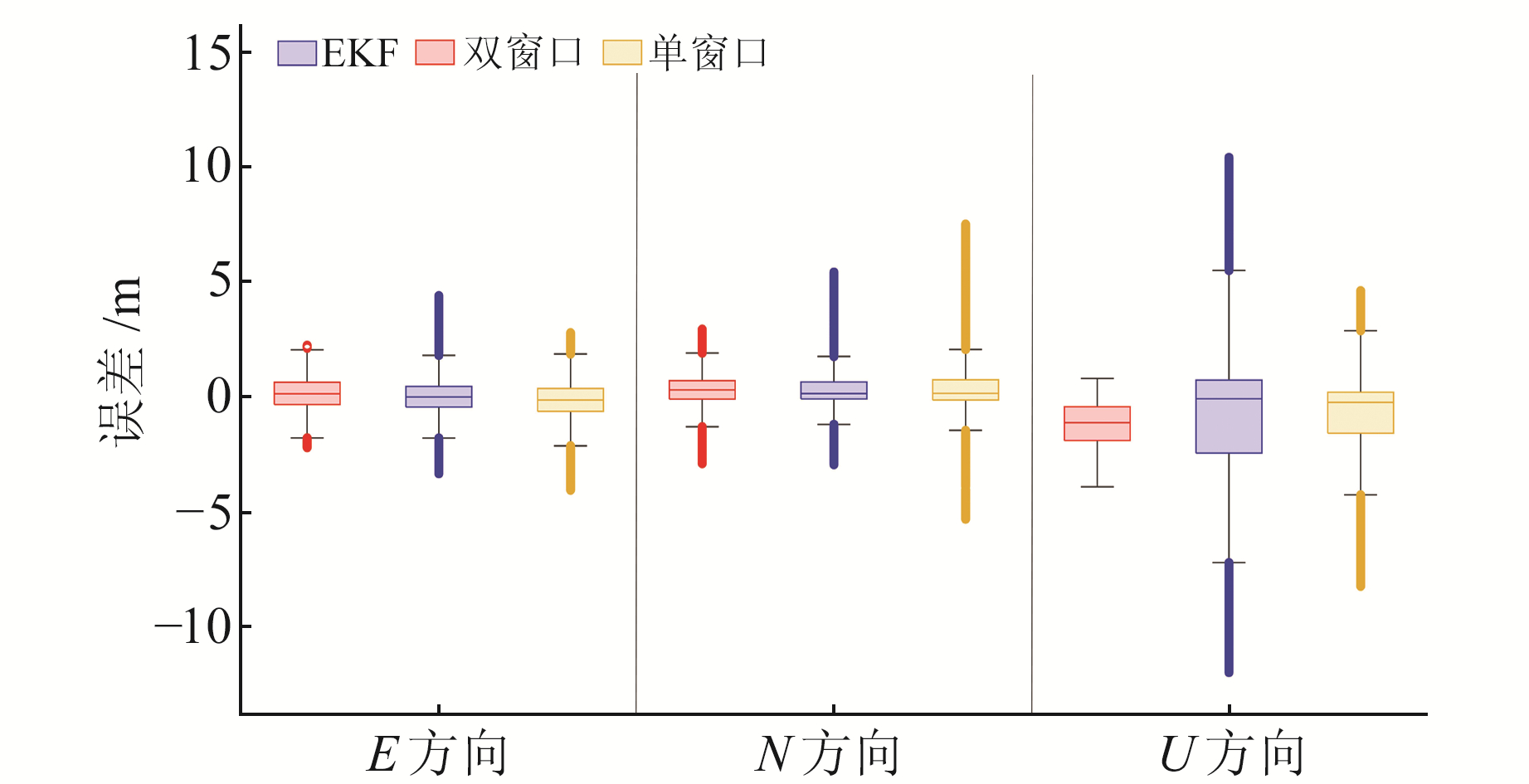
不同抗差算法位置误差的箱线图如图 5所示,由图可知,相对于EKF和单窗口Sage-Husa算法,双窗口Sage-Husa抗差算法的位置误差更集中在0 m附近,未出现偏差很大的异常值,系统稳健性更好,对于复杂环境定位精度的提升最为明显。
|
图 5 抗差算法位置误差箱线图 Fig. 5 Boxplot of position error of robust algorithm |
各算法位置误差RMS统计见表 2(单位m),由表可知,双窗口Sage-Husa抗差算法在东、北、天3个方向上的精度相较于EKF分别提升35.71%、23.93%、55.24%,相较于单窗口Sage-Husa分别提升38.98%、36.88%、24.04%。单窗口Sage-Husa在部分历元窗口内浮点解新息协方差会拉大固定解新息协方差,抗差因子的增大导致精度劣化,而双窗口对解的分类可有效避免该问题。
|
|
表 2 抗差算法位置误差RMS Tab. 2 RMS of position error of robust algorithm |
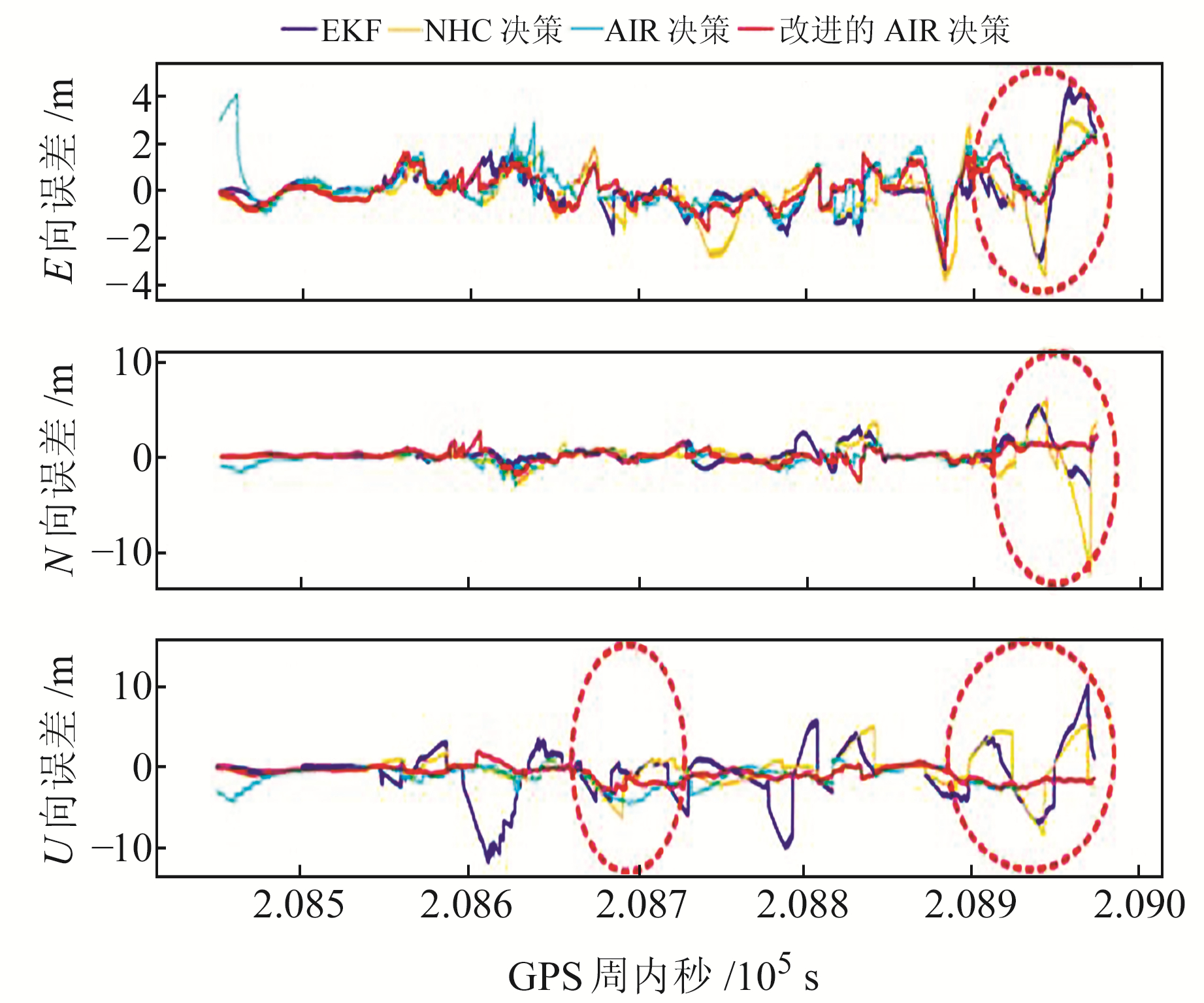
图 6为改进的异常新息占比决策对比其他决策模型应用于抗差自适应算法的位置误差曲线,图中圆圈区域表示提升明显的区域。从误差曲线可以看出,改进的异常新息占比决策的定位精度优于其他算法,传统方法会出现判断错误而导致定位精度恶化,NHC决策错误率更高。改进的决策算法可分开处理异常的伪距和载波相位新息,漏报和虚警概率大大降低,整体性能明显优于其他算法。
|
图 6 不同决策算法位置误差 Fig. 6 Position error of different decision algorithms |
图 7为不同决策算法位置误差箱线图,从图中可以看出,EKF和NHC决策算法出现明显偏离于最高和最低阈值的异常值,改进的异常新息占比决策算法在3个方向上出现异常值的次数均最低。

|
图 7 不同决策算法位置误差箱线图 Fig. 7 Boxplot of position error of different decision algorithms |
表 3(单位m)为各算法的位置误差RMS统计,由表可知,改进的异常新息占比决策算法对新息向量进行分类化处理,以及将异常新息占比阈值与观测数量相关联,使算法决策的准确率得到提升,位置均方根误差达到0.70 m、0.69 m、1.16 m,相较于EKF在东、北、天3个方向上位置精度分别提升35.78%、38.94%、66.00%;相较于NHC决策分别提升38.60%、56.33%、44.50%;相较于传统的异常新息占比决策分别提升31.37%、10.39%、32.16%。
|
|
表 3 不同决策算法位置误差RMS Tab. 3 RMS of position error of different decision algorithms |
为降低抗差自适应算法中不合适的抗差因子和决策算法的影响,研究双窗口Sage-Husa抗差算法,针对不同的GNSS状态在不同窗口中进行抗差,对传统的异常新息占比决策算法中未考虑的两个问题予以改进,并结合新息自适应算法构建改进的异常新息占比决策抗差自适应算法。实验结果表明,所提出的双窗口Sage-Husa抗差算法在复杂场景下抗差因子的构建更为稳健,定位性能优于EKF和单窗口Sage-Husa抗差算法;所提算法准确率更高,适用于复杂场景下观测质量频繁波动和出现粗差的情况,能够满足城区复杂环境下高精度定位的需求。本文后续会进一步针对自适应滤波加以研究改进,并引入第3种数据源进一步提升决策的准确率和融合定位精度。
| [1] |
Wang M K, Yu P D, Li Y Z. Performance Analysis of GNSS/INS Loosely Coupled Integration Systems under GNSS Signal Blocking Environment[J]. E3S Web of Conferences, 2020, 206
(  0) 0) |
| [2] |
Liu R X, Liu F C, Liu C N, et al. Modified Sage-Husa Adaptive Kalman Filter-Based SINS/DVL Integrated Navigation System for AUV[J]. Journal of Sensors, 2021, 2021
(  0) 0) |
| [3] |
Luo Z Y, Fu Z H, Xu Q W. An Adaptive Multi-Dimensional Vehicle Driving State Observer Based on Modified Sage-Husa UKF Algorithm[J]. Sensors, 2020, 20(23)
(  0) 0) |
| [4] |
Yang R, Zhang A J, Zhang L F, et al. A Novel Adaptive H-Infinity Cubature Kalman Filter Algorithm Based on Sage-Husa Estimator for Unmanned Underwater Vehicle[J]. Mathematical Problems in Engineering, 2020, 2020
(  0) 0) |
| [5] |
Xu T L. Adaptive Kalman Filter for INS/GPS Integrated Navigation System[J]. Applied Mechanics and Materials, 2013, 336-338: 332-335 DOI:10.4028/www.scientific.net/AMM.336-338.332
(  0) 0) |
| [6] |
Guo S L, Sun Y J, Chang L M, et al. Robust Cubature Kalman Filter Method for the Nonlinear Alignment of SINS[J]. Defence Technology, 2021, 17(2): 593-598 DOI:10.1016/j.dt.2020.03.016
(  0) 0) |
| [7] |
Yang Y X, He H D, Xu G C. Adaptively Robust Filtering for Kinematic Geodetic Positioning[J]. Journal of Geodesy, 2001, 75(2): 109-116
(  0) 0) |
| [8] |
赵方, 吴凡. GNSS/INS自适应智能组合导航算法[J]. 北京邮电大学学报, 2022, 45(2): 1-8 (Zhao Fang, Wu Fan. Adaptive Integrated Navigation Based Artificial Intelligence[J]. Journal of Beijing University of Posts and Telecommunications, 2022, 45(2): 1-8)
(  0) 0) |
| [9] |
周彬, 赵万良, 荣义杰, 等. 基于MEMS-INS/GNSS组合导航抗差自适应Kalman滤波算法[J]. 导航与控制, 2018, 17(4): 14-20 (Zhou Bin, Zhao Wanliang, Rong Yijie, et al. Robust Adaptive Kalman Filtering Algorithm for Integrated Navigation Based on MEMS-INS/GNSS[J]. Navigation and Control, 2018, 17(4): 14-20)
(  0) 0) |
| [10] |
Yang Z H, Li Z K, Liu Z, et al. Improved Robust and Adaptive Filter Based on Non-Holonomic Constraints for RTK/INS Integrated Navigation[J]. Measurement Science and Technology, 2021, 32(10)
(  0) 0) |
| [11] |
高怡, 高社生. 一种基于状态相关因子的抗差自适应滤波算法[J]. 测控技术, 2014, 33(2): 111-115 (Gao Yi, Gao Shesheng. A Robust Adaptive Filter Method Based on State Dependent Coefficient[J]. Measurement and Control Technology, 2014, 33(2): 111-115)
(  0) 0) |
| [12] |
薛文婷, 张波, 李署坚. 组合导航中一种新息自适应卡尔曼滤波算法[J]. 全球定位系统, 2014, 39(4): 8-11 (Xue Wenting, Zhang Bo, Li Shujian. Application of New Information Adaptive Kalman Filter in Integrated Navigation[J]. GNSS World of China, 2014, 39(4): 8-11)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43

