2. 武汉引力与固体潮国家野外科学观测研究站,武汉市洪山侧路40号,4300713;
3. 成都锦城学院数学建模研究中心,成都市西源大道1号,611731
微震震源定位是微震监测技术研究和实施微震监测系统的重要内容,广泛应用于矿山监测、油气田开发、大坝安全防护及文物防盗预警等领域[1]。以往的微震震源定位方法研究较多使用Geiger法、牛顿法、梯度下降法等传统数值方法计算得到微震震源的近似解,这些方法往往依赖初值选取或目标函数可微,且并行搜索能力不足,无法得到更多有效的搜索信息。随着计算机技术的发展和人工智能研究的持续深入,生物启发式的群体智能优化算法在微震震源定位研究中的应用愈发广泛,对于开展微震震源定位理论研究和开发微震监测系统具有一定的积极效果。
由于传统群体智能优化算法存在一些明显的性能缺陷[2-3],需要引入其他方法优化超参数或修改个体的更新策略[4]。近年来,新型群体智能优化算法在一定程度上对传统方法进行改进,如灰狼算法[5](gray wolf optimization,GWO)、鲸鱼优化算法[6](whale optimization algorithm,WOA)、蝗虫优化算法[7](grasshopper optimization algorithm,GOA)、麻雀搜索算法[8](sparrow search algorithm,SSA)、蚁狮算法[9](ant lion optimization,ALO)、蜻蜓算法[10](dragonfly algorithm,DA),但目前缺乏必要的对比分析实验来验证其在微震震源定位中的有效性,特别是在新方法与微震震源定位相结合后的非线性求解、大规模运算及多元寻优效果等方面。
本文选取2014年以来新提出的6种新型群体智能优化算法研究矿山微震震源定位,分析其仿生原理、核心计算公式及优缺点,设计一种新型微震震源反演数学模型,利用仿真的矿山微震震源正反演数据对比分析6种方法的性能差异,并结合实际矿山人工爆破数据再次验证并分析新型群体智能优化算法在矿山微震震源定位中的有效性和可靠程度。
1 微震震源定位数学模型微震震源定位数学模型是开展微震震源定位方法研究的基础,也是关系定位精度大小的重要因素。为便于实验分析,地震波信号采用P波信号,并假设岩体介质均匀、各向同性及地震波传播速度保持不变。
设拾震器空间位置为Ti(xi, yi, zi),微震震源位置为O(x0, y0, z0),P波波速为v,地震波初至到时为ti,发震时刻记为t0。令Δti=(ti-t0),li=
| $ \left\{\begin{array}{l} \left(x_i-x_0\right)^2+\left(y_i-y_0\right)^2+\left(z_i-z_0\right)^2= \\ \quad\left(t_i-t_0\right) \cdot v \\ \left(x_j-x_0\right)^2+\left(y_j-y_0\right)^2+\left(z_j-z_0\right)^2= \\ \quad\left(t_j-t_0\right) \cdot v \end{array}\right. $ | (1) |
式(1)中两方程除以波速v可将距离方程转换为时间方程,再将等号左右对应相减,同时为增加数学模型求解时的计算扰动,便于分析适应度值变化规律,在到时差模型中增加数值1,可得到最终的微震震源定位数学模型:
| $ f=\sum\limits_{i, j=1 ; i>j}^N\left|\left(\Delta t_i-\Delta t_j\right)-\frac{l_i-l_j}{v}+1\right|-1 \mid $ | (2) |
式中,N为微震监测系统得到的有效初至到时数量。
2 新型群体智能优化算法群体智能优化算法是指利用计算机技术学习并模仿自然界中各种生物群体的狩猎行为或趋利避害现象,以完成最优化目标的启发式方法,能实现个体与个体、个体与种群之间的信息交流,具有一定的鲁棒性、可扩展性及分布性等特点,常用于机械结构设计、最优路径决策、空间定位及图像识别等领域。本文选取2014年以来新提出的灰狼算法(GWO)、鲸鱼优化算法(WOA)、蝗虫优化算法(GOA)、麻雀搜索算法(SSA)、蚁狮算法(ALO)、蜻蜓算法(DA)等6种群体智能优化方法进行基本原理分析。
2.1 灰狼算法灰狼算法[5]是一种模仿灰狼群体捕猎行为的智能优化方法,能有效利用灰狼群体的内部社会分级制度,由头狼和高等级狼带领狼群中其他狼个体进行猎物的搜索、围捕与攻击等行为。该算法会在每次迭代后保存当前灰狼种群中适应度值最高的3个灰狼的位置信息,并在达到最大迭代次数时完成捕杀动作,即最优解为所选位置的算数平均值。
2.2 鲸鱼优化算法鲸鱼优化算法[6]是一种源自座头鲸特殊狩猎特点的群体计算方法,该方法学习鲸鱼采用口中吐出气泡来标记猎物并螺旋式捕猎目标的生物学行为。该算法具有随机搜索代理与最佳搜索代理2种寻优策略,并采用三角波函数模拟螺旋式攻击。
2.3 蝗虫优化算法蝗虫优化算法[7]是一种模仿蝗虫群体幼虫与成虫同时杂居与迁移的新型群体仿生优化算法,利用蝗虫幼虫行动迟缓和成虫移动较快的特性,便于同时开展局部搜索与全局寻优。该算法更新蝗虫位置的核心公式为:
| $ \begin{gathered} x_{i+1, d}=c\left(\sum\limits_{j=l, j \neq i}^N c \frac{u b_d-l b_d}{2}\right. \\ \left.s\left(\left|x_{j, d}-x_{i, d}\right|\right) \frac{x_j-x_i}{d_{i j}}\right)+T_d^{\prime} \end{gathered} $ | (3) |
式中,xi+1, d为第i只蝗虫个体在位置向量第d维的坐标值;c为与最大迭代次数有关,能影响蝗虫全局寻优或局部搜索能力的动态衰减系数;ubd与lbd分别为蝗虫个体位置第d维的上下限阈值;s(·)为蝗虫i受到蝗虫j影响的相互作用力函数;dij为蝗虫i与蝗虫j之间的绝对距离;Td′为蝗虫群体此前得到的最优位置。
2.4 麻雀搜索算法麻雀搜索算法[8]是一种群体智能优化算法,通过模拟麻雀群的跟随觅食现象与反偷袭预警行为,将搜索到较好食物的个体视作麻雀群的领头鸟,其他麻雀个体视作追随领头鸟的随从鸟,且为保证整个麻雀群的整体安全,也会有少量麻雀个体充当侦查鸟,直接决定整个麻雀群体是否放弃当前觅食对象,进而移动到更加安全的区域进行觅食。
2.5 蚁狮算法蚁狮算法[9]是一种模仿蚁狮幼虫狩猎蚂蚁的新型群体智能优化算法,即蚁狮幼虫通过制造砂质漏斗状的陷阱诱捕随机游走的蚂蚁。该算法充分结合蚂蚁位置的随机性、精英策略和轮盘赌方法的优点,可增强算法的全局搜索能力。
2.6 蜻蜓算法蜻蜓算法[10]是一种新型仿生优化算法,能模仿蜻蜓群体在局部区域内狩猎和进行长距离种群迁徙的生物学行为。该算法更新蜻蜓位置的核心公式为:
| $ \begin{gathered} \Delta X_{i+1}= \\ \left(s S_i+a A_i+c C_i+f F_i+e E_i\right)+w \Delta X_i \end{gathered} $ | (4) |
| $ X_{t+1}=X_t+\Delta X_{t+1} $ | (5) |
式中,Xt为第t时刻的蜻蜓个体位置;Xt+1为第t+1时刻的蜻蜓个体位置;ΔXt+1为蜻蜓个体位置更新的步长;Si、Ai、Ci、Fi、Ei分别为与第i个蜻蜓个体位置更新相关的分离因子、对齐因子、内聚因子、目标吸引因子及障碍躲避因子,s、a、c、f、e分别对应上述因子的权重值;w为惯性权重。
3 微震震源正反演仿真实验为验证本文6种新型群体智能优化算法和新设计的反演数学模型在微震震源定位中的有效性,设计3组正反演仿真实验,分别利用空间立方体台阵、平面S型台阵及人为设定异常值等条件,对比分析新算法在不同台阵、有无异常值干扰下的实验效果,并采用遗传算法(genetic algorithm,GA)作为传统方法进行微震震源定位结果对比。实验环境采用MATLAB 2019仿真平台和Windows 10的64位操作系统。
3.1 基于空间立方体台阵的微震正反演仿真实验该实验设定地震波P波在介质中传播速度为1 500 m/s,发震时刻记为2022-05-20 13:14:00,发震位置坐标统一设为(733,367,78),负责获取P波到时信息的拾震器资料如表 1和图 1所示。
|
|
表 1 基于空间立方体台阵的微震震源正演仿真数据 Tab. 1 Data of micro-seismic source forward modeling based on space cube array |
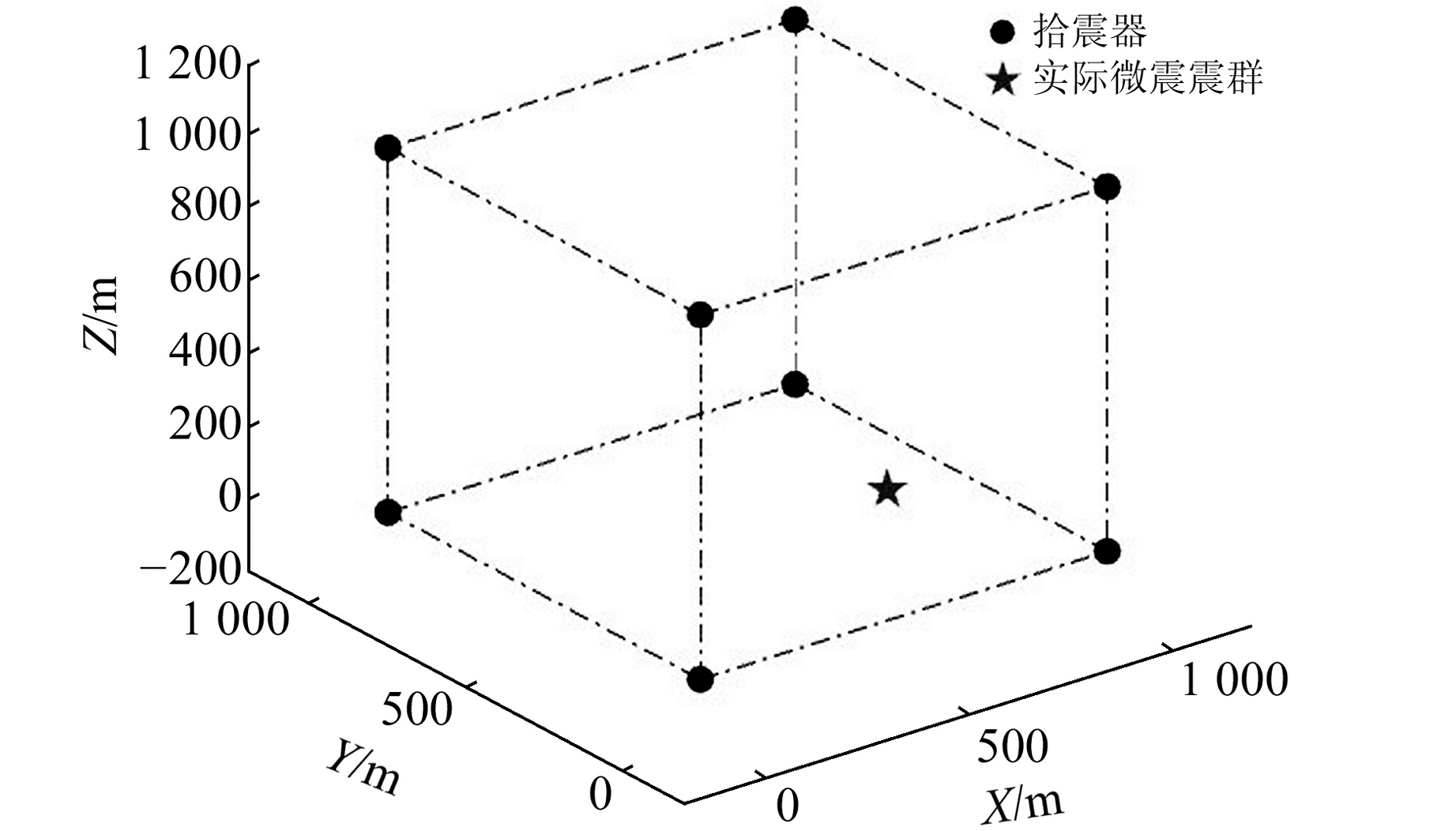
|
图 1 仿真实验拾震器布置 Fig. 1 Seismometer layout of simulation experiment |
算法中预设相关参数为:群体搜索代理(种群)数目为20,最大迭代次数为500,目标维数为4,搜索下限为[0,0,0,0],搜索上限为[1 000,1 000,1 000,10 000],初值为[0,0,0,0],定位实验循环次数为100。
图 2为基于微震震源正演仿真数据的定位结果,从图中可以看出,基于蚁狮算法的微震震源定位效果较好,在100次循环定位实验中,仅有1次出现显著异常,整体寻优效果符合预期;蜻蜓算法、鲸鱼算法和蝗虫优化算法的定位结果基本在100 m上下震荡,波形震荡幅度存在明显差异。

|
图 2 基于微震震源正演仿真数据的定位结果 Fig. 2 Localization results based on micro-seismic source simulation data |
表 2为基于微震震源正演仿真数据的定位结果统计值,其中指标Mean、STD、Best、Worst分别表示100次循环实验下微震震源定位误差的均值、标准差、最优值、最劣值,Speed、Fitness分别表示定位模型计算时间和最终适应度函数值的均值。由表可知,基于蚁狮算法的微震震源定位精度较高,Mean值可达到8.441 0m,STD也相对较小,仅为15.335 6 m,但其整体定位效果依然受到若干局部最优解的干扰(Worst值高达142.881 1 m),有进一步优化的可能性;麻雀搜索算法在6个算法中全局搜索能力较强,指标Best最优,为0.001 9 m;其他新型算法的定位结果不太理想,出现定位误差较大、循环实验结果存在较大震荡、模型求解速度较慢以及易陷入局部最优等现象,不适用于微震震源定位。另外,作为对比的传统遗传算法的定位效果亦不理想,除求解速度指标Speed略好外,其他大部分指标值皆不如新型算法。
|
|
表 2 基于空间立方体台阵的微震震源定位结果统计 Tab. 2 Statistics of micro-seismic source localization based on space cube array |
该实验基于平面S型台阵进行设计,共布设7个拾震器(图 3),发震位置坐标定为(733,367,78),分布在S型台阵一侧,其他条件设置与立方体台阵基本相同,P波到时和拾震器资料如表 3所示。

|
图 3 仿真实验拾震器布置 Fig. 3 Seismometer layout of simulation experiment |
|
|
表 3 基于平面S型台阵的微震震源正演仿真数据 Tab. 3 Data of micro-seismic source forward modeling based on plane S-shaped array |
表 4为基于平面S型台阵的微震震源定位结果统计值,由表可知,灰狼算法、麻雀搜索算法、蚁狮算法的微震震源定位效果在同类算法中表现最好,其定位误差均值Mean分别为63.210 2 m、66.520 2 m、194.326 5 m,其中麻雀搜索算法的稳定性稍差,其STD和Worst指标值皆可证明该结论;作为对比的遗传算法和蝗虫优化算法的定位效果最差,其定位结果也出现较大扰动,不宜应用在地震观测、地球物理勘探等较复杂工程中。
|
|
表 4 基于平面S型台阵的微震震源定位结果统计 Tab. 4 Statistics of micro-seismic source localization based on plane S-shaped array |
该实验通过人工设计一个异常值扰动来测试各个群体智能算法对异常值的抗干扰能力,并将1号探测器接收到的P波到时数据0.653 2 s更改为1.200 0 s,其他实验条件不变。
表 5为基于异常值扰动的微震震源定位结果统计值,从表中可以看出,几乎所有算法的定位误差均较大,但仍有部分现象值得注意:1)全部算法均出现STD大幅下滑的现象,其中蜻蜓算法的STD值下滑幅度最大,达到214.579 6 m,这与模型中增加了异常值扰动存在一定联系,扰动值会增加算法在迭代过程中捕获局部最优或近似解的概率,更易陷入到错误的搜索方向中;2)遗传算法和蜻蜓算法在增加异常值前后的微震震源定位误差均值Mean变化不大,说明这2种算法具有一定的抗干扰能力,但其Mean值均较大,这种抗干扰特性也只能理解为一种减少算法全局搜索、增强局部最优寻获概率的能力,没有实质上的定位应用价值,从Best指标值的大幅增加亦可验证这一点;3)Fitness值显著远离适应度函数值的理论零值,这与该模型数据中掺杂有异常值的现象相符。
|
|
表 5 基于异常值扰动的微震震源定位结果统计 Tab. 5 Statistics of micro-seismic source localization based on exception value |
为验证6种新型群体优化算法和定位数学模型的有效性,采用湖南柿竹园微震实验数据[11]进行验证,该数据来源于2008年建设有30通道的柿竹园钨多金属矿微震监测系统,主要用来监测本区域的矿柱开裂、坍塌等地压变化。微震事件信息包括人工爆破位置为(8 732.70,6 570.60,511.30),起爆时刻为10:27,爆破成功后观测到8个P波到时数据,重新标记为T1~T8,具体信息如表 6所示。
|
|
表 6 湖南柿竹园钨多金属矿微震事件数据 Tab. 6 Micro-seismic event data of polymetallic mine in Shizhuyuan |
算法中预设相关参数为:群体搜索代理(种群)数目为20,最大迭代次数为500,目标维数为4,搜索下限为[1, 1, 1, 1],搜索上限为[10 000,10 000,10 000,10 000],初值为[0,0,0,0],定位实验循环次数为100。图 4为基于柿竹园微震事件的微震震源定位结果,从图中可以看出,在100次循环定位实验中,基于蚁狮算法的微震震源定位效果较好,定位误差基本分布在[20,30]之间,且多数数据点较接近30 m水平线;麻雀搜索算法、鲸鱼优化算法和蝗虫优化算法出现局部极大值,这会对算法寻优的稳定性造成严重破坏;蜻蜓算法和灰狼算法的微震震源定位结果误差较大,易陷入到局部最优中。
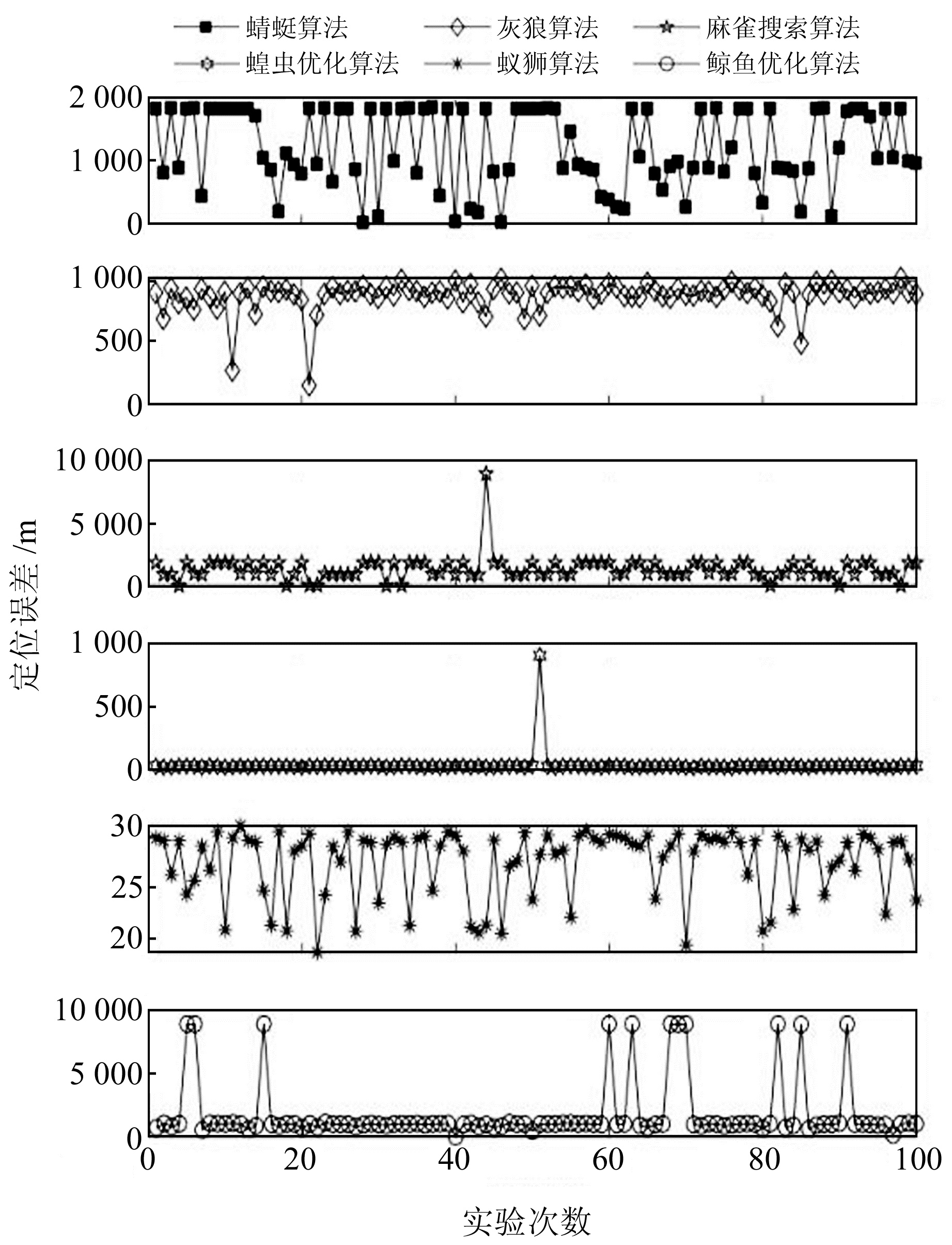
|
图 4 基于柿竹园微震事件的微震震源定位结果 Fig. 4 Results of micro-seismic source localization of polymetallic mine in Shizhuyuan |
表 7为基于柿竹园微震事件的定位结果统计,由表可知,基于蚁狮算法的微震震源定位性能较好,其Mean、STD值分别可达到27.408 1 m和3.337 2 m,Speed与Fitness值也基本符合预期,分别为1.154 1 s和0.173 1,整体定位效果明显优于其他同类方法,这与表 2中利用微震震源正演仿真数据得到的定位结果相符;蝗虫优化算法的微震震源定位效果仅次于蚁狮算法,定位误差均值可达到35.140 3 m;其他方法的定位精度基本都在1 000~2 000 m之间,较不理想。
|
|
表 7 基于柿竹园微震事件的定位结果统计 Tab. 7 Statistics of micro-seismic source localization of polymetallic mine in Shizhuyuan |
图 5为100次循环实验下的微震震源定位结果箱线图,可用来反映多组微震震源定位结果的数据离散程度与数学统计信息,图中箱子上下边界线指示值分别代表定位结果的上四分位数与下四分位数,箱内实线表示定位结果的中位数,“+”标志数据被判定为异常点。由图可知,蝗虫优化算法和蚁狮算法的微震震源定位精度整体相当,但是蝗虫优化算法出现一例异常值(定位误差偏大),其在算法稳健性上稍差于蚁狮算法;其他算法的定位误差较大,存在显著的异常点离群、数据波动或左偏态现象,不适用于微震震源定位。
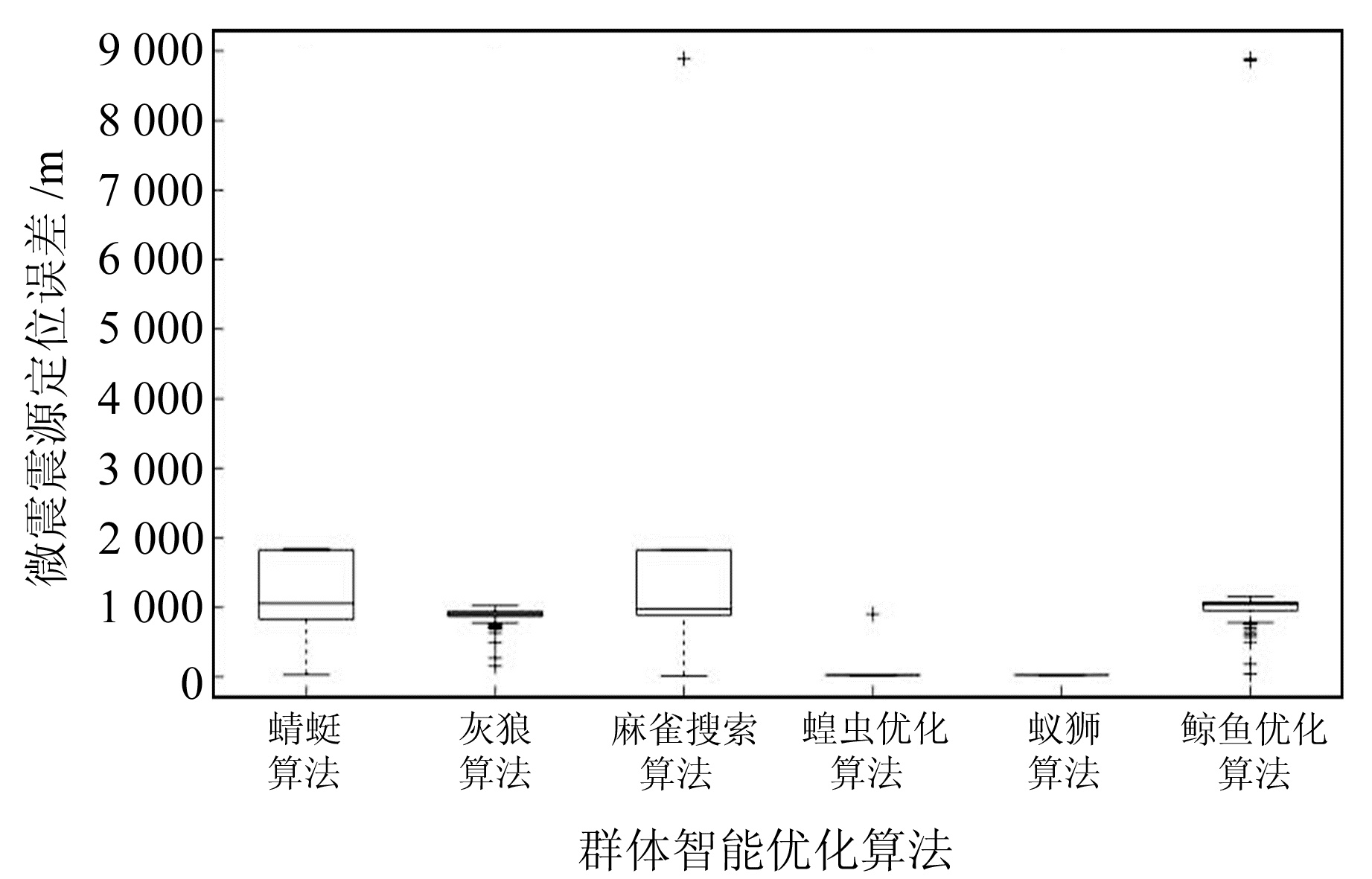
|
图 5 微震震源定位结果箱线图 Fig. 5 Boxplot of micro-seismic source localization results |
为了解新型智能优化算法与传统优化算法的定位性能差异,采用遗传算法、模拟退火算法、模式搜索算法(pattern search algorithm)等进行对比分析。表 8为基于传统优化算法的微震震源定位结果,其反演数学模型和优化条件与新型群体智能优化算法实验基本相同,整体来看,3种方法的微震震源定位结果皆不理想,模式搜索算法相较于其他两种算法的定位误差稍小,且搜索结果极为稳定;而传统智能优化算法中遗传算法和模拟退火算法表现出较大的算法寻优缺陷,Best指标表明其全局搜索能力存在不足,在100次定位实验中均未捕获理想的微震震源近似解。
|
|
表 8 传统优化算法的微震震源定位结果统计 Tab. 8 Statistics of micro-seismic source localization of traditional optimization algorithm |
本文研究并采用2014年以来新提出的6种群体智能优化算法,对比讨论这些方法在微震震源定位中的可行性与合理性,并结合微震震源正演仿真数据和工程爆破数据,利用一系列实验和定位效果多维度评价指标加以验证,得到以下结论:
1) 相较于其他智能算法,蚁狮算法整体寻优性能优秀,定位误差均值、标准差、最劣值及适应度函数均值等多个指标在全部算法中稳居前三,并在空间立方体正反演仿真实验和柿竹园微震定位实验中表现相对最佳,结果波动性较小,更加适用于微震震源定位。
2) 相对于蚁狮算法,灰狼算法在部分指标上具有一定优势,其求解速度在各个算法中最快,亦在微震正反演仿真实验中表现优异,但应用在一定存在数据误差的微震事件中时,定位精度不高,算法抗干扰能力不甚理想。
本文研究结果有望弥补新型群体智能优化算法在微震震源定位研究中的缺失或不足,可为后续的定位方法改进与精度提高提供有价值的研究方向。在后续研究中,将加强新型群体智能算法在微震震源定位中收敛性能与稳定性分析,讨论多种异常干扰值(如拾震器坐标误差或P波误差)和数据误差分布类型(如正态分布、F分布、半正态分布)的影响。
| [1] |
李翔, 徐奴文. 微震震源定位研究现状及展望[J]. 地球物理学进展, 2020, 35(2): 598-607 (Li Xiang, Xu Nuwen. Research Developments and Prospects on Microseismic Source Location[J]. Progress in Geophysics, 2020, 35(2): 598-607)
(  0) 0) |
| [2] |
庞聪, 李查玮, 马武刚, 等. 基于粒子群优化算法和F分布的微震源三步定位方法[J]. 高原地震, 2022, 34(4): 35-40 (Pang Cong, Li Chawei, Ma Wugang, et al. A Three-Step Localization Method for Micro-Seismic Sources Based on Particle Swarm Optimization and F-Distribution[J]. Plateau Earthquake Research, 2022, 34(4): 35-40)
(  0) 0) |
| [3] |
尹奇峰, 潘冬明, 郭全仕, 等. 基于快速模拟退火算法的井中微地震事件定位反演[J]. 地球物理学进展, 2019, 34(5): 1-1 961 (Yin Qifeng, Pan Dongming, Guo Quanshi, et al. Inversion of Borehole Microseismic Event Location Based on Fast Simulated Annealing Algorithm[J]. Progress in Geophysics, 2019, 34(5): 1-1 961)
(  0) 0) |
| [4] |
郭一楠, 崔宁, 程健. 基于MOPSO-SA混合算法的矿山微震震源定位方法[J]. 煤炭科学技术, 2020, 48(3): 126-132 (Guo Yinan, Cui Ning, Cheng Jian. Microeismic Source Localization Method Based on Hybrid Algorithm of MOPSO-SA[J]. Coal Science and Technology, 2020, 48(3): 126-132)
(  0) 0) |
| [5] |
Emary E, Yamany W, Hassanien A E, et al. Multi-Objective Gray-Wolf Optimization for Attribute Reduction[J]. Procedia Computer Science, 2015, 65: 623-632 DOI:10.1016/j.procs.2015.09.006
(  0) 0) |
| [6] |
庞聪, 王磊, 马武刚, 等. 地震与爆破波形信号的EEMD多尺度分布熵提取和WOA-SOM神经网络识别研究[J]. 大地测量与地球动力学, 2022, 42(9): 980-984 (Pang Cong, Wang Lei, Ma Wugang, et al. EEMD Multiscale Distribution Entropy Extraction and WOA-SOM Recognition between Seismic and Blast Waveform Signals[J]. Journal of Geodesy and Geodynamics, 2022, 42(9): 980-984)
(  0) 0) |
| [7] |
Saremi S, Mirjalili S, Lewis A. Grasshopper Optimisation Algorithm: Theory and Application[J]. Advances in Engineering Software, 2017, 105: 30-47
(  0) 0) |
| [8] |
Wang P, Zhang Y, Yang H W. Research on Economic Optimization of Microgrid Cluster Based on Chaos Sparrow Search Algorithm[J]. Computational Intelligence and Neuroscience, 2021, 2021
(  0) 0) |
| [9] |
Mirjalili S. The Ant Lion Optimizer[J]. Advances in Engineering Software, 2015, 83: 80-98
(  0) 0) |
| [10] |
Mirjalili S. Dragonfly Algorithm: A New Meta-Heuristic Optimization Technique for Solving Single-Objective, Discrete, and Multi-Objective Problems[J]. Neural Computing and Applications, 2016, 27(4): 1 053-1 073
(  0) 0) |
| [11] |
吕进国, 姜耀东, 赵毅鑫, 等. 基于稳健模拟退火-单纯形混合算法的微震定位研究[J]. 岩土力学, 2013, 34(8): 2 195-2 203 (Lü Jinguo, Jiang Yaodong, Zhao Yixin, et al. Study of Microseismic Positioning Based on Steady Simulated Annealing-Simplex Hybrid Algorithm[J]. Rock and Soil Mechanics, 2013, 34(8): 2 195-2 203)
(  0) 0) |
2. Wuhan Gravitation and Solid Earth Tides, National Observation and Research Station, 40 Hongshance Road, Wuhan 430071, China;
3. Mathematical Modeling Research Center, Chengdu Jincheng College, 1 Xiyuan Road, Chengdu 611731, China
 2023, Vol. 43
2023, Vol. 43


