滑坡区预测对于更快、更安全地实施滑坡防治方案具有重要意义,国内外学者对此进行大量研究。郭科等[1]提出利用多传感器目标跟踪融合技术来处理滑坡多个点的监测数据;陈明金等[2]采用分级式数据融合结构和基于遗传神经网络的融合算法提取滑坡特征信息获得完整的滑坡特征时间序列。Krka Acˇ等[3]提出基于随机森林的滑坡运动预测方法;Li等[4]提出基于迭代组合策略的滑坡预测方法;Chen等[5]结合遗传算法和模拟退火算法对网络权值和偏差进行优化,然后进行滑坡预测。王利等[6]利用互信息和改进粒子群优化的长短期记忆神经网络进行滑坡监测多源数据融合,同时采用遗传算法优化循环神经网络层数和每层网络记忆体来确定最佳参数组合。随着传感器技术、计算机技术、网络通信技术等在滑坡监测领域的应用,滑坡监测预警也向自动化、智能化方向发展[7-10]。
近年来,深度学习已取得很大进展。Elman神经网络结构较为简单,具备较强的计算能力与稳定性,但由于结构参数具有随机性,容易陷入局部最优解。针对该问题,以往研究大多针对GA、BA、SA、SSA、PSO、ACO、WOA、GWO等算法来优化神经网络的权值阈值,将多种智能算法优势互补来优化神经网络可以取得更好的效果。因此,本文将具备全局搜索能力的遗传算法和具备局部搜索能力的粒子群算法相结合的融合算法(GA-PSO)对Elman神经网络结构参数进行优化,以确定最终的结构参数,新算法在具备原有算法优势的基础上可以获得更好的寻优性能及稳定性[9]。
1 Elman神经网络 1.1 Elman神经网络原理及结构算法Elman神经网络是一种既有局部记忆单元又有局部反馈连接的动态反馈型递归神经网络,具有良好的自适应、自组织以及较强的学习、容错和抗干扰能力[11]。Elman神经网络是在BP神经网络结构基础上,在隐含层增加一个承接层,作为一步延时算子,达到记忆目的,从而使系统具有适应时变特性的能力[12],增强网络全局稳定性,比前馈型神经网络具有更强的计算能力。
Elman神经网络由输入层、隐含层、承接层和输出层组成[13]。包含承接层的神经元与隐含层神经元一一对应,隐含层的输出值经过延迟后反馈到承接层。承接层通常能够记忆隐含层上一时刻的状态,因此Elman网络具有状态记忆功能,这是其能够反映动态系统的本质[14]。Elman神经网络结构如图 1所示。

|
图 1 Elman神经网络模型结构 Fig. 1 Structure of Elman neural network model |
Elman神经网络结构特点是在连续有限的时间段内,网络能够根据信息之间的互传和参数调整以任意精度逼近所期望的精度。Elman神经网络数学模型公式如下:
| $ x(k)=f\left(\omega_{r j} x_0(k)+\omega_{i j} u(k-1)\right) $ | (1) |
| $ x_c(k)=\alpha x_c(k-1)+x(k-1) $ | (2) |
| $ y(k)=g\left(\omega_{j l} x(k)\right) $ | (3) |
式中,k表示时刻;ωrj为承接层与隐含层的连接权;ωij为输入层与隐含层的连接权;ωjl为隐含层与输出层的连接权;x(k)、xc(k)、y(k)分别表示隐含层单元、承接层单元和输出层单元的输出;0≤α < 1为自连接反馈增益因子;f(x)为隐含层传递函数,选择sigmoid函数作为激励函数;g(x)表示输出层函数,为中间层输出的线性组合,选取线性函数purelin。对于递归神经网络,网络输出不仅与k时刻的输入有关,而且与k以前时刻的输入信号有关,因此涉及精度计算时必须采用动态学习规则。训练算法采用Levenberg-Marquardt(LM)算法,作为训练神经网络常用的一种算法,具有较快的收敛速度。设第k次迭代网络的实际输出为yi(k),期望输出为qi(k),网络误差性能函数E可表示为[15]:
| $ E(k)=\frac{1}{2} \sum\limits_{i=1}^n\left(q_i(k)-y_i(k)\right)^2 $ | (4) |
网络权值变化为:
| $ \boldsymbol{\omega}(k+1)=\boldsymbol{\omega}(k)+\varepsilon\left(-\frac{\partial E(k)}{\partial \boldsymbol{\omega}}\right)+\alpha \Delta \boldsymbol{\omega}(k) $ | (5) |
式中,ω为第k次迭代各层之间的连接权向量;ε为学习速率。
1.2 隐含层节点选取本文模型采用Elman神经网络模型,其隐含层节点数具有关键作用,节点数不同,均方根误差就会存在较大差异。为得到最佳隐含层节点数,使均方根误差达到最小,首先采用经验公式确定节点数范围,计算公式如下:
| $ p=\sqrt{m+n}+a $ | (6) |
式中,p为隐含层节点数,m和n分别为输入层和输出层节点数,a为1~10的常数,本文模型隐含层节点数p的取值范围为3 < p < 12。将隐含层节点数初始值设置为2,每次加1,直到12为止,通过计算得出隐含层节点数为7时均方根误差最小。
2 GA-PSO-Elman神经网络模型 2.1 遗传算法遗传算法(genetic algorithm, GA)是基于生物进化原理的一种多点搜索全局性优化算法。该算法将问题参数编码为染色体,再利用迭代方式进行选择、交叉以及变异等运算来交换种群中染色体信息,最终生成符合优化目标的染色体[14]。核心内容分为4部分,分别为参数编码、初始种群设定、适应度函数设计、选择交叉变异操作。本文预测模型将模型训练的预估值与期望值的误差作为适应度函数。
2.2 粒子群优化算法粒子群优化(particle swarm optimization, PSO)算法类似于遗传算法,但与之相比,该算法参数少,简单易于实现,在每次迭代中粒子不断更新速度和位置进行搜索,以跟踪最优粒子,具有较强的局部搜索能力。速度更新和位置更新公式可表示为:
| $ \begin{gathered} V_{i d}^{k+1}=\omega V_{i d}^k+c_1 r_1\left(P_{i d}^k-X_{i d}^k\right)+ \\ c_2 r_2\left(P_{g d}^k-X_{i d}^k\right) \end{gathered} $ | (7) |
| $ X_{i d}^{k+1}=X_{i d}^k+V_{i d}^{k+1} $ | (8) |
式中,Xid为粒子位置,Vid为粒子移动速度,Pidk和Pgdk分别为粒子位置最优值与在种群位置中最优值。
2.3 GA-PSO-Elman神经网络模型建立Elman神经网络能以任意精度逼近任意非线性函数,但其初始化权值和阈值为区间[0, 1]之间的随机数,初始化参数的随机性会影响网络模型预测结果的精度和稳定性。
GA作为一种全局寻优算法,在解决全局优化问题上效果很好,具有较强的全局搜索能力,但其局部搜索能力欠佳,容易陷入局部最优解。同时GA不具备记忆能力,如果在迭代过程中种群发生变化,会导致之前的信息消失[16]。PSO具备记忆能力,在每次迭代中,粒子会通过个体极值和群体极值来更新自身速度和位置,以及更新公式来计算适应度值,对比之后保留最优解。但PSO存在过早收敛问题,原因为搜索空间中种群多样性损失,而GA算法的交叉变异操作可保证种群多样性。在新模型中,将神经网络训练数据的输入权值和隐含层节点阈值映射为GA种群中染色体信息,先利用GA全局搜索能力选出最优染色体构成最优种群,再利用PSO局部搜索能力选出最优个体,该算法将求解权值阈值问题转化为寻找最优染色体问题。
因此将GA与PSO算法优势互补,组合成遗传粒子群混合优化算法(GA-PSO),同时结合Elman神经网络在非线性模型的映射能力,构建遗传算法与粒子群优化的Elman神经网络模型(GA-PSO-Elman),融合后的算法全局收敛性好、收敛速度快、鲁棒性高。算法流程如图 2所示。
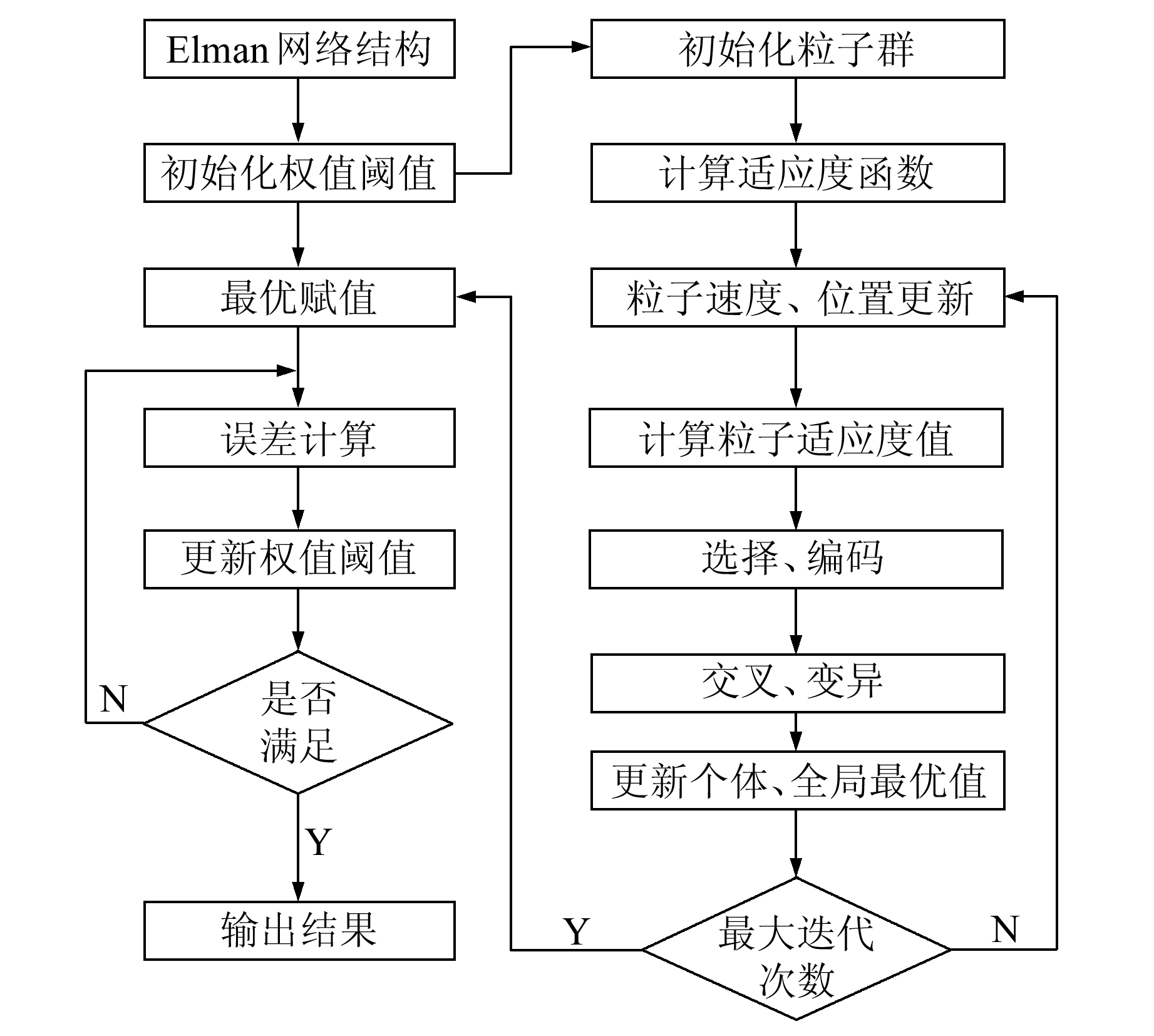
|
图 2 优化Elman网络模型权值阈值流程 Fig. 2 Flowchart of optimizing weight and threshold of Elman network model |
该模型优化过程如下:
1) 初始化种群,将种群随机初始化为N个子群;
2) 计算适应度,适应度函数见式(4);
3) 根据式(7)、(8)更新粒子速度和位置;
4) 进行选择、交叉、变异操作;
5) 更新个体最优值和全局最优值,重复执行直到达到预设的最大迭代次数即可结束该过程;
6) 将GA-PSO混合算法寻优的最优权值阈值赋予神经网络。
3 Elman神经网络模型工程应用 3.1 研究区概况及监测点分布为验证本文模型的有效性,以黑方台党川滑坡为例进行实验分析。黑方台位于甘肃省永靖县盐锅峡镇,所处位置为36°04′10″~36°07′20″N、103°16′40″~103°20′50″E,属于黄河Ⅳ级阶地[7],总面积约13.7 km2。台塬顶部和底部平均高差大于70 m,滑坡主体距离下方居民区水平距离约400 m,除自身地质条件外,降雨和灌溉造成地下水位抬升是导致该区域滑坡频发的重要因素。黑方台先后发生多次黄土滑坡,对输电通讯等造成较大影响。根据滑坡成因、范围、地形地貌特征,在滑坡变形监测点布设GNSS监测设备,设备均位于该台塬边缘(图 3),附近发育多条裂缝[17]。

|
图 3 滑坡监测点分布 Fig. 3 Distribution of landslide monitoring points |
为分析滑坡位移变化量与环境影响因子的相关程度,将各环境因子变量和滑坡位移变化量的相关性及显著性作为指标(表 1),进一步研究环境因子对滑坡位移变化量预测精度的影响。相关性结果可表明这两个变量之间的实际意义,显著性结果则决定这两个变量之间的统计学意义[7],一般取95%置信概率,即显著性小于0.05可认为湿度和累积降水与滑坡位移量之间存在显著性,故可将湿度和累积降水量加入到输入变量与累积位移量共同作为训练数据,研究滑坡累积位移量与湿度和降水量的关系(图 4)。
|
|
表 1 滑坡位移量与各环境因子之间的相关性及显著性 Tab. 1 Correlation and significance between landslide displacement and each environmental factor |

|
图 4 HF06监测点累积位移量与湿度和降水关系 Fig. 4 Relationship between accumulated displacement and humidity and precipitation at HF06 monitoring point |
在该滑坡体上布设12个GNSS监测设备,实时捕捉mm级滑坡位移形变,各个监测点的累积位移数据具有同步效应,此次选取HF06监测点数据进行实验。以2019-04-05~09-11共160 d监测值作为训练数据,预测2019-09-12~10-01共20 d滑坡位移量。
为验证新建模型的有效性,分别采用传统BP神经网络(BP)、遗传算法优化BP神经网络(GA-BP)、Elman神经网络、遗传算法优化Elman神经网络(GA-Elman)、遗传粒子群优化Elman神经网络(GA-PSO-Elman)5种预测模型对滑坡变形进行预测,将不同方案得到的预测结果与实测值对比来评估预测结果的可靠性。
从图 5可以看出,Elman神经网络由于具有适应时变特性的能力,与传统BP神经网络相比,具有较强的全局稳定性,其预测值更逼近实际值;当采用GA对初始化参数进行优化后,传统BP神经网络和Elman神经网络模型的预测精度均有所提高;GA-PSO-Elman网络模型由于网络初始化结构参数同时具有全局最优性和局部最优性,模型预测精度更高。
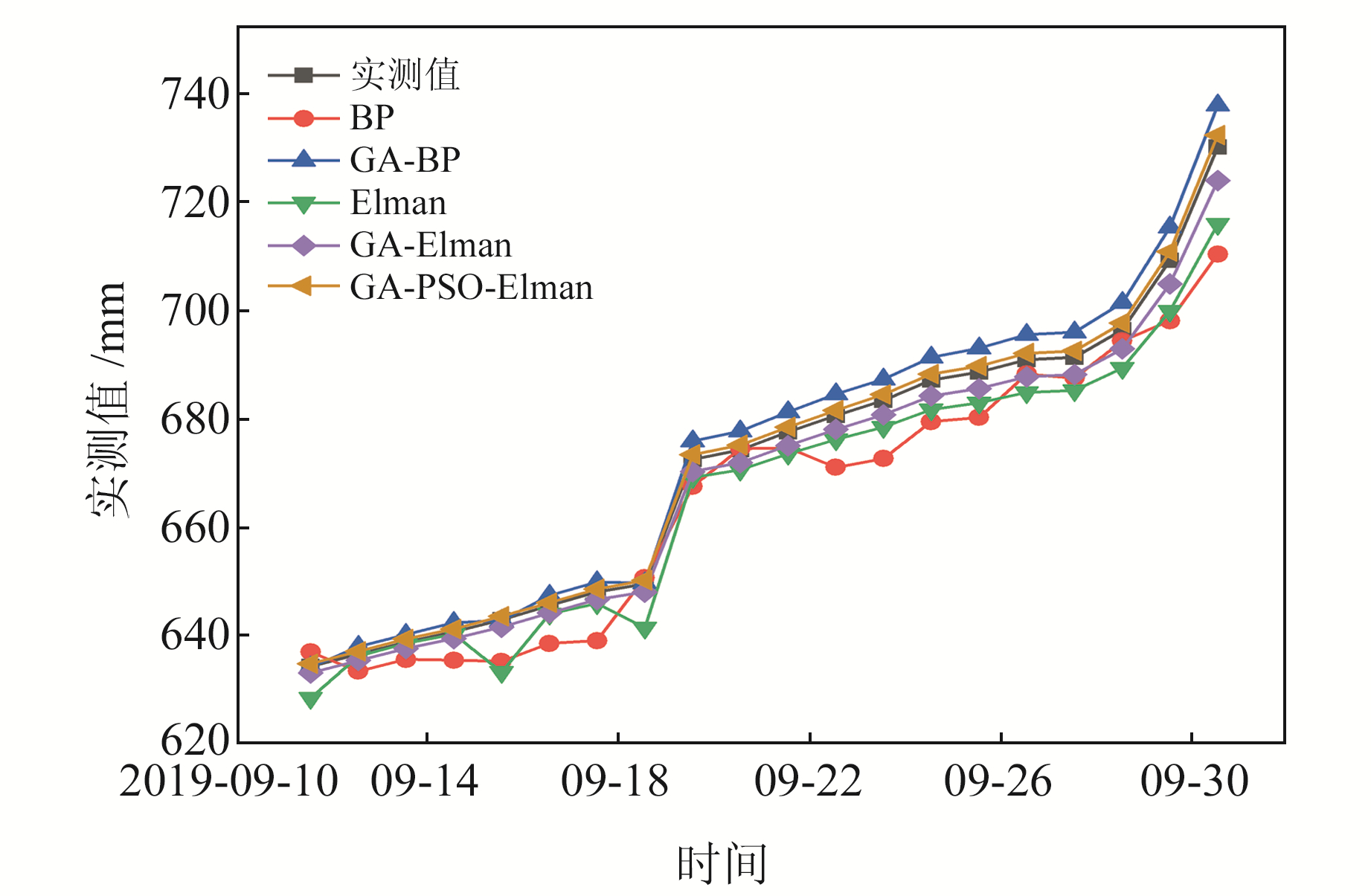
|
图 5 HF06点预测变形量与实测结果对比 Fig. 5 Comparison of predicted deformation and measured results at HF06 point |
以实测值与预测值的误差平方和作为适应度函数绘制各方案的适应度曲线(图 6),判断种群个体适应度是否符合优化准则,适应度越小,则预测效果越好。从神经网络的迭代适应度曲线可以看出,GA-PSO-Elman网络模型具有最小的适应度,而且迭代收敛速度更快,迭代过程较平稳。
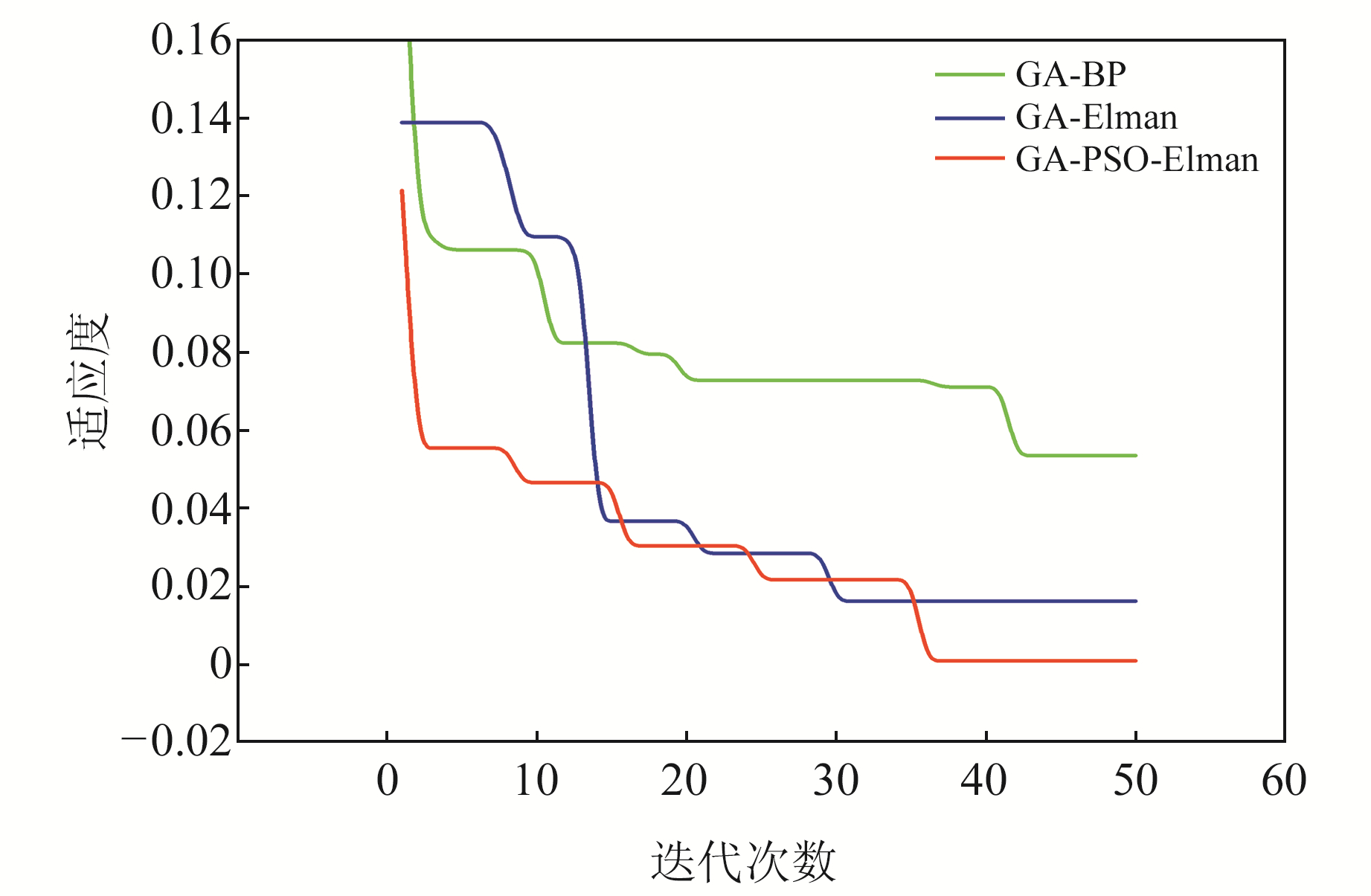
|
图 6 神经网络模型适应度曲线 Fig. 6 Fitness curve of neural network model |
通过表 2可以看出,GA-BP与GA-Elman模型的预测值与实测值误差分别在8 mm和7 mm以内,而且误差在所预测的20 d中逐渐增大,这是由于该滑坡在预测期间处于临滑阶段,较前1 d位移变化量更大。GA-PSO-Elman网络模型的预测值与实测值绝对误差最大为2.2 mm,最小为0.49 mm。将各个模型预测值与实测值的不符值绘制成样条曲线(图 7),从图中可以看出,5种模型预测不符值整体在[-5, 5]范围内波动,尤其是GA-PSO-Elman模型,其预测不符值整体最接近0。
|
|
表 2 HF06点变形预测值与实测值的不符值 Tab. 2 Discrepancy values between predicted and measured values at HF06 point |
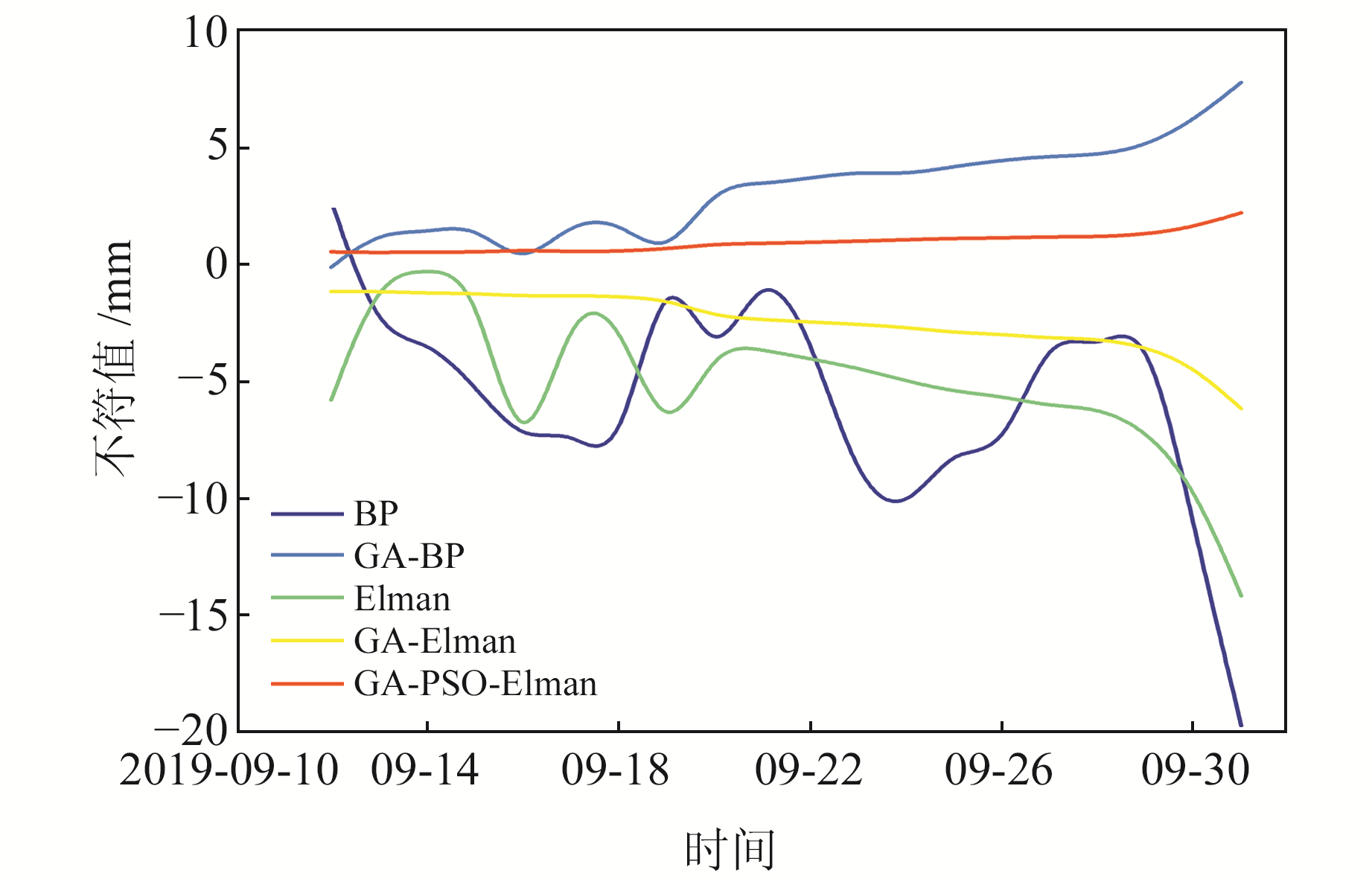
|
图 7 各个模型实测值与预测值的不符值 Fig. 7 Discrepancy values between measured and predicted values of each model |
根据该模型的位移预测值可以得到变形速率或加速度以及切线角,当预测值达到或超过设定的预警指标时,预警系统发出预警指令,相关部门可采取相应的应急措施进行预防治理。此次预测实验时段为2019-04~10,为该滑坡的加速变形阶段,该监测点于2019-10-05失稳。
3.4 模型精度检验为评价模型的准确性,采用3个评价指标:平均绝对误差(MAE)、均方根误差(RMSE)和拟合优度(R2),对应公式如下:
| $ \mathrm{MAE}=\frac{1}{n} \sum\limits_{i=1}^n\left|x_i-x_i^{\prime}\right| $ | (9) |
| $ \mathrm{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(x_i-x_i^{\prime}\right)^2} $ | (10) |
| $ R^2=1-\frac{\sum\limits_{i=1}^n\left(x_i-x_i^{\prime}\right)^2}{\sum\limits_{i=1}^n\left(x_i-\bar{x}_i\right)^2} $ | (11) |
式中,xi、x′i分别为真实值和预测值,n为预测数量个数。BP、GA-BP、Elman、GA-Elman、GA-PSO-Elman五种模型的预测误差对比结果见表 3,可以看出GA-PSO-Elman模型预测精度最高。
|
|
表 3 HF06监测点各个模型预测精度对比 Tab. 3 Comparison of prediction accuracy of each model at HF06 monitoring point |
1) 结合遗传算法和粒子群优化算法的新型寻优算法,可实现全局搜索和局部搜索的平衡,能够有效优化Elman神经网络的初始权值和阈值,提高黄土滑坡预测精度。
2) 动态Elman神经网络比静态BP神经网络效果好,预测精度和收敛速度明显提高。经过GA-PSO优化的Elman神经网络模型可取得更好的预测效果,均方根误差达到1.03,拟合优度达到0.998。因此,该方法具有较好的应用前景和进一步的研究发展前景。
| [1] |
郭科, 彭继兵, 许强, 等. 滑坡多点数据融合中的多传感器目标跟踪技术应用[J]. 岩土力学, 2006, 27(3): 479-481 (Guo Ke, Peng Jibing, Xu Qiang, et al. Application of Multi-Sensor Target Tracking to Multi-Station Monitoring Data Fusion in Landslide[J]. Rock and Soil Mechanics, 2006, 27(3): 479-481)
(  0) 0) |
| [2] |
陈明金, 欧阳祖熙, 范国胜. 基于数据融合的滑坡综合监测信息提取方法[J]. 大地测量与地球动力学, 2007, 27(6): 77-81 (Chen Mingjin, Ouyang Zuxi, Fan Guosheng. On Information Extraction Method Based on Data Fusion for Integrated Landslide Monitoring[J]. Journal of Geodesy and Geodynamics, 2007, 27(6): 77-81)
(  0) 0) |
| [3] |
Krkač M, Špoljarić D, Bernat S, et al. Method for Prediction of Landslide Movements Based on Random Forests[J]. Landslides, 2017, 14(3): 947-960 DOI:10.1007/s10346-016-0761-z
(  0) 0) |
| [4] |
Li L, Zhang S X, Qiang Y, et al. A Landslide Displacement Prediction Method with Iteration-Based Combined Strategy[J]. Mathematical Problems in Engineering, 2021, 2021
(  0) 0) |
| [5] |
Chen H Q, Zeng Z G. Deformation Prediction of Landslide Based on Improved Back-Propagation Neural Network[J]. Cognitive Computation, 2013, 5(1): 56-62 DOI:10.1007/s12559-012-9148-1
(  0) 0) |
| [6] |
王利, 许豪, 舒宝, 等. 利用互信息和IPSO-LSTM进行滑坡监测多源数据融合[J]. 武汉大学学报: 信息科学版, 2021, 46(10): 1 478-1 488 (Wang Li, Xu Hao, Shu Bao, et al. A Multi-Source Heterogeneous Data Fusion Method for Landslide Monitoring with Mutual Information and IPSO-LSTM Neural Network[J]. Geomatics and Information Science of Wuhan University, 2021, 46(10): 1 478-1 488)
(  0) 0) |
| [7] |
王智伟, 王利, 黄观文, 等. 基于BP神经网络的滑坡监测多源异构数据融合算法研究[J]. 地质力学学报, 2020, 26(4): 575-582 (Wang Zhiwei, Wang Li, Huang Guanwen, et al. Research on Multi-Source Heterogeneous Data Fusion Algorithm of Landslide Monitoring Based on BP Neural Network[J]. Journal of Geomechanics, 2020, 26(4): 575-582)
(  0) 0) |
| [8] |
樊俊青. 面向滑坡监测的多源异构传感器信息融合方法研究[D]. 武汉: 中国地质大学, 2015 (Fan Junqing. Research on Multi-Source Heterogeneous Sensor Information Fusion for Landslide Monitoring[D]. Wuhan: China University of Geosciences, 2015)
(  0) 0) |
| [9] |
嵇胜, 李桂芳, 疏利生. 基于GAPSO-Elman神经网络算法的短时航迹预测[J]. 航空计算技术, 2021, 51(1): 60-63 (Ji Sheng, Li Guifang, Shu Lisheng. Short-Term Trajectory Prediction Based on GAPSO-Elman Neural Network Algorithm[J]. Aeronautical Computing Technique, 2021, 51(1): 60-63)
(  0) 0) |
| [10] |
蒋齐嘉. 基于多测点信息的滑坡智能预测预警方法研究[D]. 长沙: 长沙理工大学, 2021 (Jiang Qijia. Study on Intelligent Prediction and Early Warning Method of Landslide Based on Multi-Point Information[D]. Changsha: Changsha University of Science and Technology, 2021)
(  0) 0) |
| [11] |
张颖. 基于Elman网络的滑坡动态预测及控制系统研究[D]. 武汉: 华中科技大学, 2020 (Zhang Ying. Research on Landslide Dynamic Prediction and Control System Based on Elman Neural Network[D]. Wuhan: Huazhong University of Science and Technology, 2020)
(  0) 0) |
| [12] |
张琪琪. 改进粒子群算法优化Elman神经网络的交通流预测[D]. 西安: 长安大学, 2019 (Zhang Qiqi. Improved Particle Swarm Optimization for Elman Neural Network Traffic Flow Prediction[D]. Xi'an: Chang'an University, 2019)
(  0) 0) |
| [13] |
乔世范, 王超. 基于遗传模拟退火算法的滑坡位移预测方法[J]. 土木与环境工程学报, 2021, 43(1): 25-35 (Qiao Shifan, Wang Chao. Landslide Displacement Prediction Based on the Genetic Simulated Annealing Algorithm[J]. Journal of Civil and Environmental Engineering, 2021, 43(1): 25-35)
(  0) 0) |
| [14] |
陈煌琼. 基于神经网络的滑坡预测及其控制研究[D]. 武汉: 华中科技大学, 2013 (Chen Huangqiong. Research on Landslide Prediction and Controlling Based on Artificial Neural Networks[D]. Wuhan: Huazhong University of Science and Technology, 2013)
(  0) 0) |
| [15] |
李寻昌, 叶君文, 李葛, 等. 基于滑坡监测数据的Elman神经网络动态预测[J]. 煤田地质与勘探, 2018, 46(3): 113-120 (Li Xunchang, Ye Junwen, Li Ge, et al. Elman Neural Network Dynamic Prediction Based on Landslide Monitoring Data[J]. Coal Geology and Exploration, 2018, 46(3): 113-120)
(  0) 0) |
| [16] |
赵航. PSO-GA-BP神经网络在机器人无标定系统中的应用与研究[D]. 长春: 长春工业大学, 2020 (Zhao Hang. Application and Research of PSO-GA-BP Neural Network in Robot Uncalibrated System[D]. Changchun: Changchun University of Technology, 2020)
(  0) 0) |
| [17] |
李璐, 瞿伟, 张勤, 等. 优化循环神经网络在滑坡位移预测中的应用[J]. 大地测量与地球动力学, 2022, 42(6): 594-600 (Li Lu, Qu Wei, Zhang Qin, et al. Application of Optimized Recurrent Neural Network in Prediction of Landslide Displacement[J]. Journal of Geodesy and Geodynamics, 2022, 42(6): 594-600)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


