准确监测地震期间的地壳形变，对地震预警和参数反演具有重要意义^[1-2]。传统地震监测主要依靠强震仪等加速度测量设备，其采集的数据为仪器所在位置的地表加速度值，测量精度和采样率较高，对地震的高频振动很敏感，但需要经过二次积分才能还原同震位移。由于地震中地表形变导致仪器发生偏转倾斜，其记录的加速度值会存在基线漂移，积分结果会出现较大偏差^[3-5]。GNSS的快速发展为地震监测提供了新手段，其获取的是测站的坐标变化，能直接得到地表形变，不会出现强震仪的基线漂移问题和量程限制，对同震位移的监测具有可靠性。目前GNSS系统的观测频率已经达到1~50 Hz，高频GNSS观测能够获取低频、永久位移信号，对计算地震震级、滑动分布、地震矩张量具有重要意义^[6-9]。但由于采样率的提高，高频GNSS噪声会影响微弱地表形变的识别，而且高频GNSS的采样率相比强震仪仍然不足，对地震波准确到来时刻的记录会存在偏差，进而影响震中位置的确定。因此，将高频GNSS与强震仪联合使用，可获取准确可靠的同震位移结果，对地震预警和反演具有重要意义^[10-13]。本文基于Kalman滤波建立顾及基线偏差改正的高频GNSS和强震仪组合模型，将基线偏差作为未知参数实时估计，以提高数据融合的效果和稳定性，并以2016年意大利北部6.0级地震为例验证模型的有效性。

1 方法及流程 1.1 GNSS精密单点定位

相对于差分定位，精密单点定位(PPP)无需选择远离震源的参考站作为基准站，单站即可监测瞬时地壳形变。本文采用动态PPP方法解算高频GNSS，采用无电离层组合，其观测方程为：

$ \begin{gathered} P_{\mathrm{IF}}=\frac{f_1^2 \cdot P_1-f_2^2 \cdot P_2}{f_1^2-f_2^2}= \\ \rho+c \mathrm{~d} t+d_{\text {trop }}+\varepsilon\left(P_{\mathrm{IF}}\right) \end{gathered} $

(1)

$ \begin{gathered} \mathit{\Phi }_{\mathrm{IF}}=\frac{f_1^2 \cdot \mathit{\Phi }_1-f_2^2 \cdot \mathit{\Phi }_2}{f_1^2-f_2^2}=\rho+c \mathrm{~d} t+d_{\text {trop }}+ \\ \frac{c f_1^2 N_1-c f_2^2 N_2}{f_1^2-f_2^2}+\varepsilon\left( \mathit{\Phi }_{\mathrm{IF}}\right) \end{gathered} $

(2)

式中，P_i、Φ_i分别为伪距观测值和载波相位观测值，ρ、c、dt分别为星地距离、光速和接收机钟差，f_i、d_trop、N_i、ε分别为频率、对流层延迟、整周未知数和观测噪声。

1.2 顾及基线偏差改正的高频GNSS和强震仪组合模型

强震仪在震时记录的加速度存在基线漂移，本文基于Kalman滤波利用高频GNSS位移进行校正，并将基线漂移作为待估参数，融合加速度和高频GNSS位移，以准确细致地描述震时同震形变。

为进行数据融合，在地震期间，将观测站或地面视为连续线性系统，在E、N、U方向上描述测站坐标的变化情况，其运动状态方程可表示为：

$ \dot{x}_t=\boldsymbol{A}_1 x_t+\boldsymbol{B}_1 a_t+\boldsymbol{C}_1 \theta_t $

(3)

式中，$\dot{x}_t=\left[\begin{array}{l}v_t \\ a_t\end{array}\right], x_t=\left[\begin{array}{l}d_t \\ v_t\end{array}\right]$，a_t、d_t、v_t分别为加速度、位移和速度，θ_t为系统噪声，$\boldsymbol{A}_1=\left[\begin{array}{ll}0 & 1 \\ 0 & 0\end{array}\right], $，$\boldsymbol{B}_1=\left[\begin{array}{l}0 \\ 1\end{array}\right]$，$\boldsymbol{C}_1=\left[\begin{array}{l}0 \\ 1\end{array}\right]$。

Kalman滤波是在时间序列上根据观测值对状态预测值进行实时更新的方法，融合高频GNSS位移数据和强震仪加速度数据需要将GNSS位移作为观测量，加速度作为状态量。为了实时校正加速度基线漂移，将其作为状态参数估计偏差值，并视为随机游走过程：

$ \begin{gathered} \hat{a}=a+u+\alpha+\theta \\ \alpha \sim N\left(0, \sigma_a^2\right), \theta \sim N\left(0, \sigma_\theta^2\right) \end{gathered} $

(4)

式中，$\hat{a}$、a、u分别为测站真实加速度、强震仪观测加速度和基线偏差，σ_a²、σ_θ²分别为强震仪观测噪声和基线偏差过程噪声。

建立的卡尔曼滤波状态和观测方程为：

$ \boldsymbol{X}_{k+1}=\boldsymbol{A}_{k+1, k} \boldsymbol{X}_k+\boldsymbol{B}_{k+1, k} a_k+\delta_k, \delta_k \sim N\left(0, \boldsymbol{Q}_k\right) $

(5)

$ \boldsymbol{Z}_{k+1}=\boldsymbol{H}_{k+1} \boldsymbol{X}_{k+1}+\beta_{k+1}, \beta_{k+1} \sim N\left(0, \boldsymbol{R}_{k+1}\right) $

(6)

式中，$\boldsymbol{X}_k=\left[\begin{array}{l}d_k \\ v_k \\ u_k\end{array}\right]$，d_k、v_k、u_k分别为待估位移、速度和基线偏差，a_k为地震仪加速度值，δ_k为状态噪声，Z_k+1为高频GNSS位移，β_k+1为观测噪声。强震仪采样间隔为τ_a，高频GNSS采样间隔为τ_d，系数矩阵分别为：$\boldsymbol{A}_{k+1, k}=\left[\begin{array}{ccc}1 & \tau_a & 0 \\ 0 & 1 & \tau_a \\ 0 & 0 & 1\end{array}\right], \boldsymbol{B}_{k+1, k}$$=\left[\begin{array}{c}\tau_a^2 / 2 \\ \tau_a \\ 0\end{array}\right], \boldsymbol{H}_{k+1}=\left[\begin{array}{lll}1 & 0 & 0\end{array}\right]$。噪声方差矩阵分别为：状态噪声协方差矩阵Q_k= $\left[\begin{array}{ccc}\left(\sigma_a^2+\sigma_\theta^2\right) \cdot \tau_a^3 / 3 & \left(\sigma_a^2+\sigma_\theta^2\right) \cdot \tau_a^2 / 2 & \sigma_\theta^2 \cdot \tau_a^2 / 2 \\ \left(\sigma_a^2+\sigma_\theta^2\right) \cdot \tau_a^2 / 2 & \left(\sigma_a^2+\sigma_\theta^2\right) \cdot \tau_a & \sigma_\theta^2 \cdot \tau_a \\ \sigma_\theta^2 \cdot \tau_a^2 / 2 & \sigma_\theta^2 \cdot \tau_a & \sigma_\theta^2\end{array}\right]$，观测噪声协方差矩阵$\boldsymbol{R}=\frac{r}{\tau_d}$，r为高频GNSS位移测量噪声方差。

由上述状态和观测方程组成高频GNSS和强震仪组合模型，初始化状态向量和方差阵后，基于Kalman滤波不断递推，进行状态估计和测量校正，得到经过基线漂移校正的融合位移和速度。递推方程如下：

$ \hat{\boldsymbol{X}}_{k+1, k}=\boldsymbol{A}_{k+1, k} \hat{\boldsymbol{X}}_k+\boldsymbol{B}_{k+1, k} a_k $

(7)

$ \boldsymbol{P}_{k+1, k}=\boldsymbol{A}_{k+1, k} \boldsymbol{P}_k \boldsymbol{A}_{k+1, k}^{\mathrm{T}}+\boldsymbol{Q}_k $

(8)

$ \boldsymbol{K}_{k+1}=\boldsymbol{P}_{k+1, k} \boldsymbol{H}_{k+1}^{\mathrm{T}}\left(\boldsymbol{H}_{k+1} \boldsymbol{P}_{k+1, k} \boldsymbol{H}_{k+1}^{\mathrm{T}}+\boldsymbol{R}_{k+1}\right)^{-1} $

(9)

$ \hat{\boldsymbol{X}}_{k+1}=\hat{\boldsymbol{X}}_{k+1, k}+\boldsymbol{K}_{k+1}\left(\boldsymbol{Z}_{k+1}-\boldsymbol{H}_{k+1} \hat{\boldsymbol{X}}_{k+1, k}\right) $

(10)

$ \begin{gathered} \boldsymbol{P}_{k+1}=\left(\boldsymbol{I}-\boldsymbol{P}_{k+1, k} \boldsymbol{H}_{k+1}^{\mathrm{T}}\left(\boldsymbol{H}_{k+1} \boldsymbol{P}_{k+1, k} \boldsymbol{H}_{k+1}^{\mathrm{T}}+\right.\right. \\ \left.\boldsymbol{R})^{-1} \boldsymbol{H}_{k+1}\right) \boldsymbol{P}_{k+1, k} \end{gathered} $

(11)

式中，$\hat{\boldsymbol{X}}_{k+1, k}$为一步预测值，Q_k为状态噪声协方差矩阵，R_k+1为观测噪声协方差矩阵，P为误差协方差矩阵，K_k+1为增益矩阵，$\hat{\boldsymbol{X}}_{k+1}$为滤波估计值。

经过以上方程不断递推，通过卡尔曼滤波实现利用高频GNSS位移对强震仪加速度计算得到的位移和速度进行校正，能够消除加速度记录在震时出现的基线漂移现象，提高地表形变获取的准确度和精度。由于高频GNSS位移和强震仪加速度采样率不同，为了融合高频GNSS位移和强震仪加速度，使组合滤波后的位移序列具有高采样率，需要对Kalman滤波进行模型改进，即以强震仪加速度的采样时间为基准，当该历元存在GNSS位移观测值时，利用GNSS位移校正加速度基线漂移，当只存在加速度观测值时，只作状态预测而不校正。由此可实现高频GNSS和强震仪监测数据融合，获取有效、准确的同震位移。

1.3 高频GNSS和强震仪数据融合流程

高频GNSS和强震仪数据的主要融合流程为：1)对GPS、GLONASS观测值进行组合定位，解算方法为动态PPP，并通过空间叠加滤波法削弱其系统误差，获取符合实际形变变化的GNSS位移序列；2)对强震仪观测加速度值进行预处理，去除零点均值；3)建立顾及基线偏差改正的高频GNSS/强震仪组合模型；4)基于改进的Kalman滤波更新递推得到融合位移和速度。融合方法流程如图 1所示。

2 实验与分析 2.1 高频GNSS数据与强震仪数据

使用2016-08-24意大利中部M_W6.0地震期间近场所记录的高频GNSS和强震仪数据进行实验。为校正强震仪数据并与高频GNSS数据进行融合，选择2个直线距离为25 m的GNSS台站与强震台站视为并址台站，相关信息如表 1所示，其中GNSS数据采样率为10 Hz，强震仪数据采样率为200 Hz。本次实验高频GNSS观测数据和强震仪观测数据分别由意大利国家地球物理与火山研究所(INGV)和美国工程强震数据中心(CEMSD)提供。

2.2 高频GNSS共模误差分析

动态PPP解算模式由于需要精密产品支撑，定位结果可能存在系统误差，为了提高定位精度，可以在一定空间范围内将其视为共模误差。共模误差是指GNSS坐标序列中一种与空间相关的误差，区域内所有测站均受到具有空间相关性误差的影响^[14-15]。因此，动态PPP定位结果中的系统误差可以通过区域空间叠加法来削弱，改正模型为：

$ V=\sum\limits_{n=1}^i\left(\omega_i \cdot V_i\right) / \sum\limits_{n=1}^i \omega_i $

(12)

式中，i、ω_i、V_i、V分别为用于获得共模误差的基准站个数、建模时第i个基准站的权重、第i个基准站的定位偏差(动态PPP解减去静态解)、共模误差改正值。

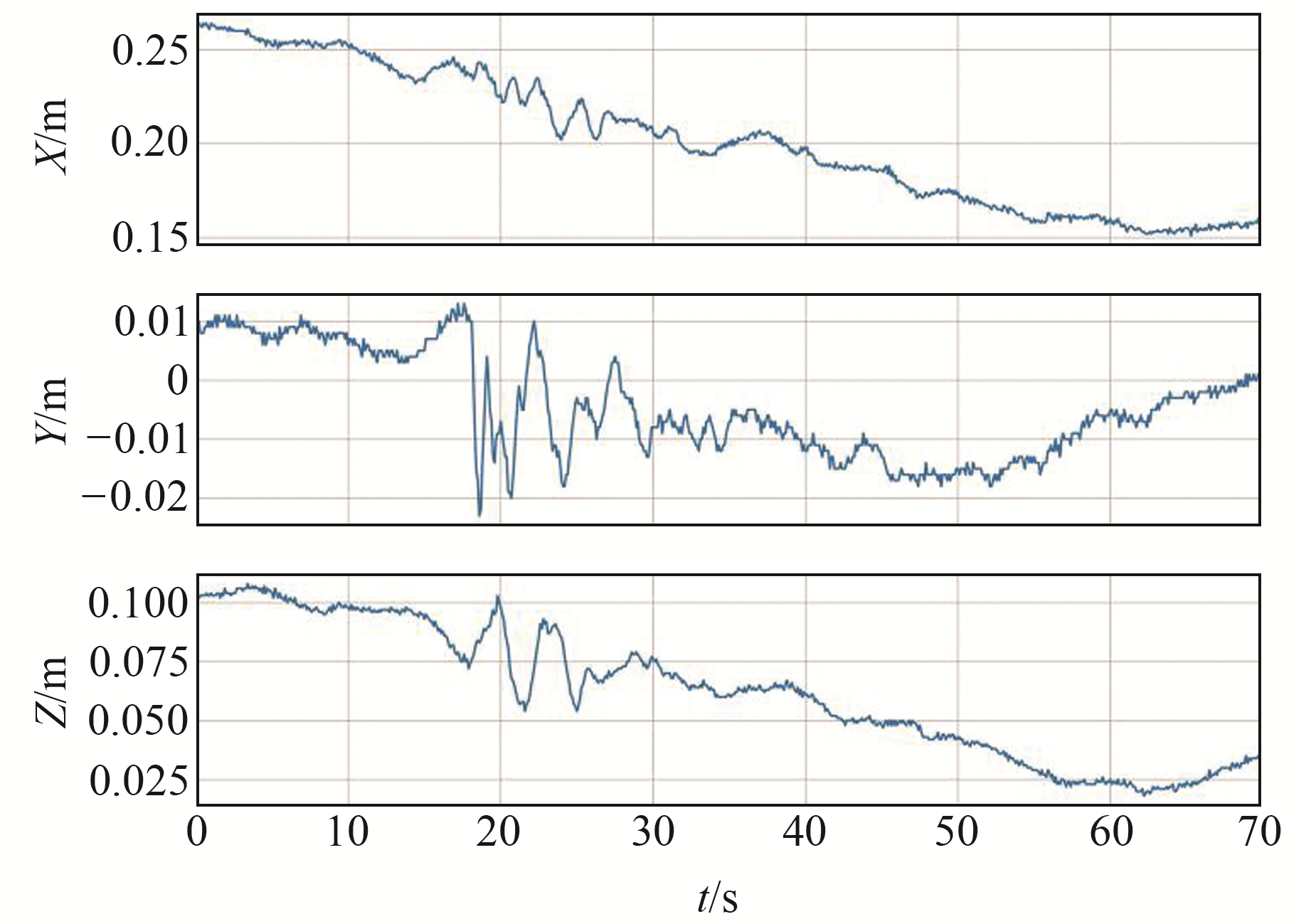
图 2为MTER站动态PPP解算结果在地震期间70 s时间窗口内的GNSS坐标序列。从图中可以明显看出，X、Y、Z坐标受到误差影响。为了削弱系统误差的影响，本文同时选取地震附近区域的2个GNSS站ACQU和RIFL，计算其定位偏差。由图 3可知，以X方向为例，其定位偏差在时间序列上趋于一致，因此可以基于空间叠加滤波法利用ACQU和RIFL站改正MTER站坐标结果存在的系统误差。

2.3 高频GNSS和强震仪数据融合与分析

首先采用动态PPP方法解算MTER站高频GNSS数据，PPP处理策略见表 2。基于GPS+GLONASS双系统组合定位，得到测站坐标时间变化序列，利用ACQU和RIFL站改正MTER站坐标系统误差，空间叠加滤波采用等权建模，即每个基准站权重相同，改正后E、N、U方向坐标如图 4所示。由于强震仪数据采用ENU坐标，为实现数据融合，需统一两者坐标系，因此在GNSS位移时间序列滤波改正后将地心地固坐标转化为站心坐标。强震仪监测数据为测站加速度值，经二次积分得到E、N、U方向位移序列，结果如图 4所示。为便于分析，选取地震期间70 s时间窗口内的位移序列进行比较。由图 4可知，经过空间叠加滤波法改正后的坐标序列在E、N、U方向上符合实际形变变化，其系统误差被削弱，经高频GNSS解算并滤波改正后E、N、U方向上精度分别为0.68 cm、0.76 cm、3.59 cm。从图中能明显观察出地震期间GNSS观测站在3个分量上的动态位移变化，但受到高频噪声和残余模型误差影响，高频GNSS对震前震后静态位移的描述能力稍弱。对比高频GNSS位移，强震仪二次积分后位移存在明显的基线漂移现象，主要是强震仪对加速度测量较为敏感，而地震导致的仪器旋转和倾斜等会引起基线偏差，在积分过程中被放大，积分结果出现较大的位移偏差和趋势现象。

利用本文融合模型得到的同震位移如图 5所示，由图可知，由于高频GNSS位移受控制，整体趋势偏差被消除，强震仪数据的基线漂移现象得到校正，融合后位移具有与强震仪观测值同样的时间分辨率。由于强震仪数据的输入，融合位移在震前和震后更为平滑，GNSS位移高频噪声得到控制，更有利于震前地震波到来时刻的精确提取；经过数据融合，可削弱U方向上GNSS误差波动，使最终位移更准确。相比单一传感器，融合位移在精度上提升较大，更能反映震时地表动态位移变化和最终的同震永久阶跃位移。

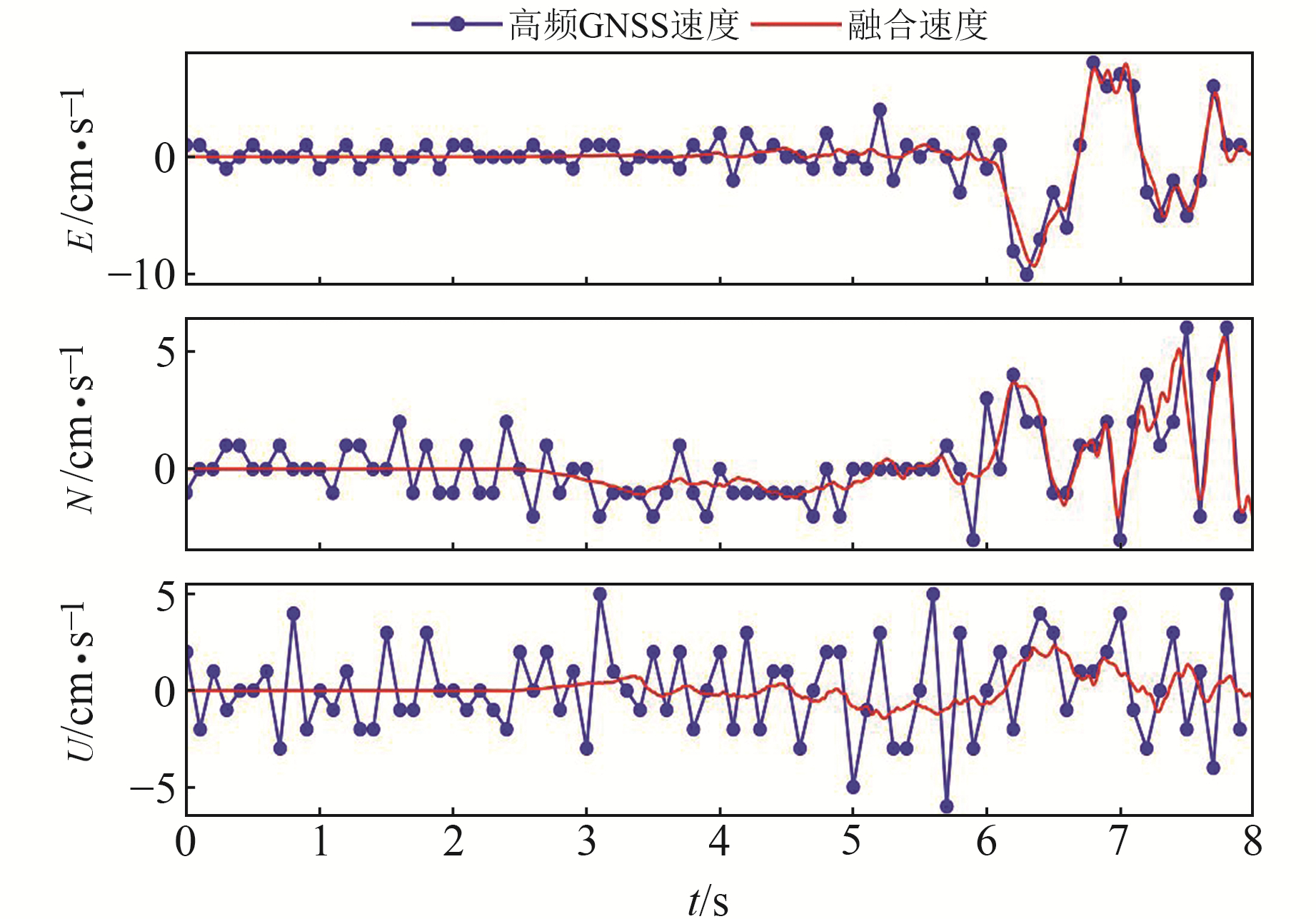
图 6为截取震前到地震时刻的速度片段，从图中可以看出，高频GNSS获取的速度受高频噪声影响，在地震波到来时对扰动不敏感，无法准确拾取地表形变开始时刻。将2种数据融合得到的速度对形变变化的描述效果更好，能够明显观察到速度序列因地震波到来而开始波动变化。融合速度相比高频GNSS速度在精度和时间分辨率上均更优，更有利于拾取地震P波到时，提高地震预警和参数反演的准确性。

3 结语

本文融合高频GNSS与强震仪2种观测技术，提出高频GNSS和强震仪数据组合方法。首先采用PPP技术解算高频GNSS数据得到GNSS位移，然后基于Kalman滤波算法融合高频GNSS位移和强震观测加速度值，利用GNSS位移校正强震仪加速度基线偏差，获取融合位移，建立顾及基线偏差改正的高频GNSS和强震仪组合模型。以2016年意大利北部6.0级地震监测数据为例，探究联合高频GNSS和强震仪观测获取同震位移和速度的数据融合方法及其优势。实验结果表明，融合后位移和速度精度更高，同时具有GNSS位移的可靠性和加速度值的高采样率等优势，对同震位移的分段性描述更准确，有利于P波到时拾取和地表最终位移确定，对于地震的准确监测和预警具有重要意义。