2. 中国地震局地震大地测量重点实验室,武汉市洪山侧路40号,430071
地震的自动检测和震相到时拾取是地震数据处理的关键步骤,对地震速报和编目工作至关重要。近年来,随着国家地震烈度速报与预警工程的不断发展,台站布置越来越密集,数据也呈爆炸式增长,人工处理已无法满足地震预警、地震要素快速产出等实时信息获取的需求。近年来,基于深度学习的地震检测和震相拾取方法取得了较大进展,国内外相继研发出许多震相拾取的深度学习模型,在地震检测能力、到时拾取精度和处理效率等方面都有明显提升[1-4]。但上述模型能否广泛应用于不同区域进行地震事件检测定位,取决于其泛化能力。为分析各模型的普适性,本文利用湖北台网50个台站的事件波形构建数据集,测试PhaseNet和EQTransformer模型在湖北台网中的泛化能力,并对模型拾取的震相到时与人工震相目录作对比,分析深度学习模型的优势、适用范围和存在的不足。
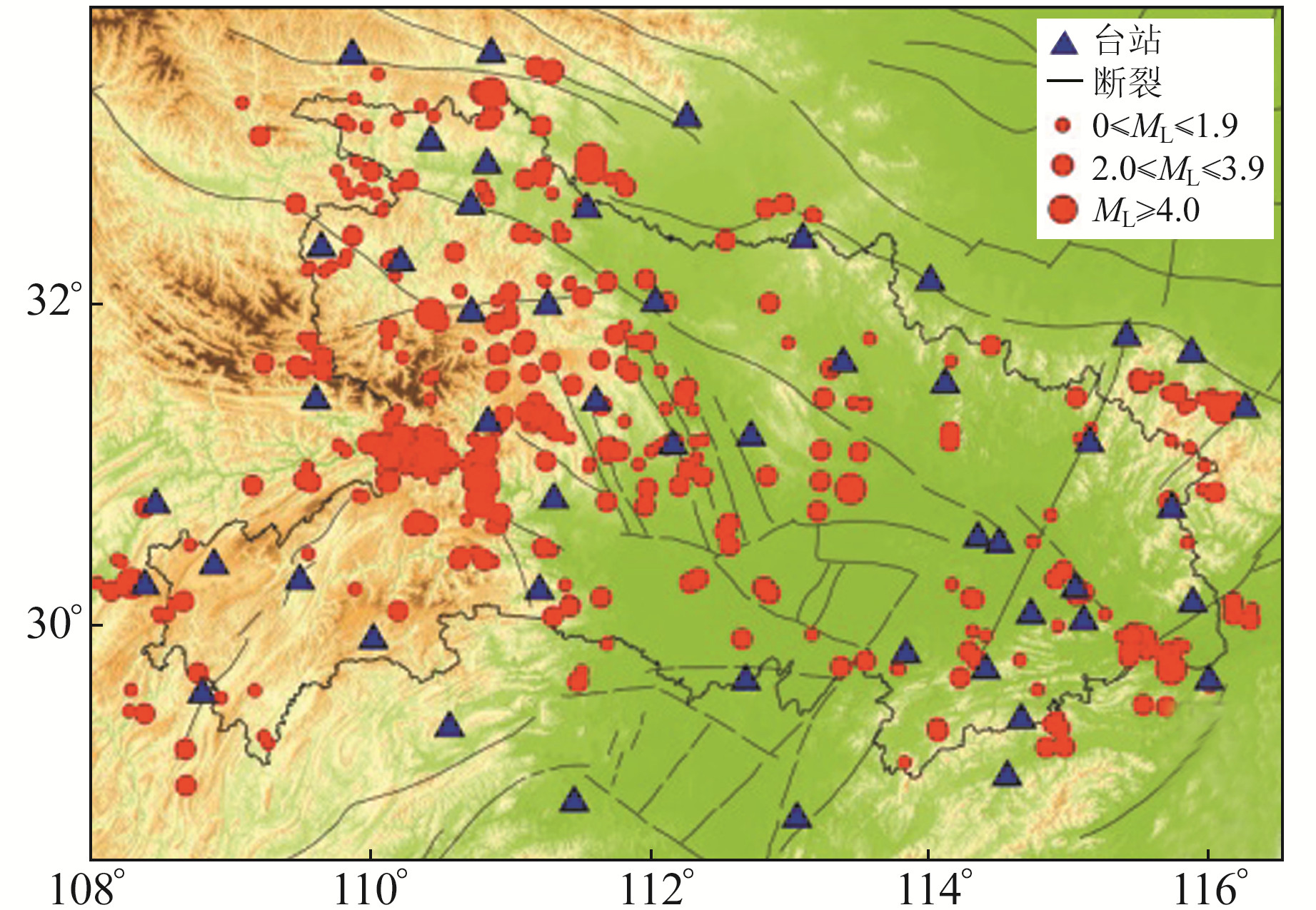
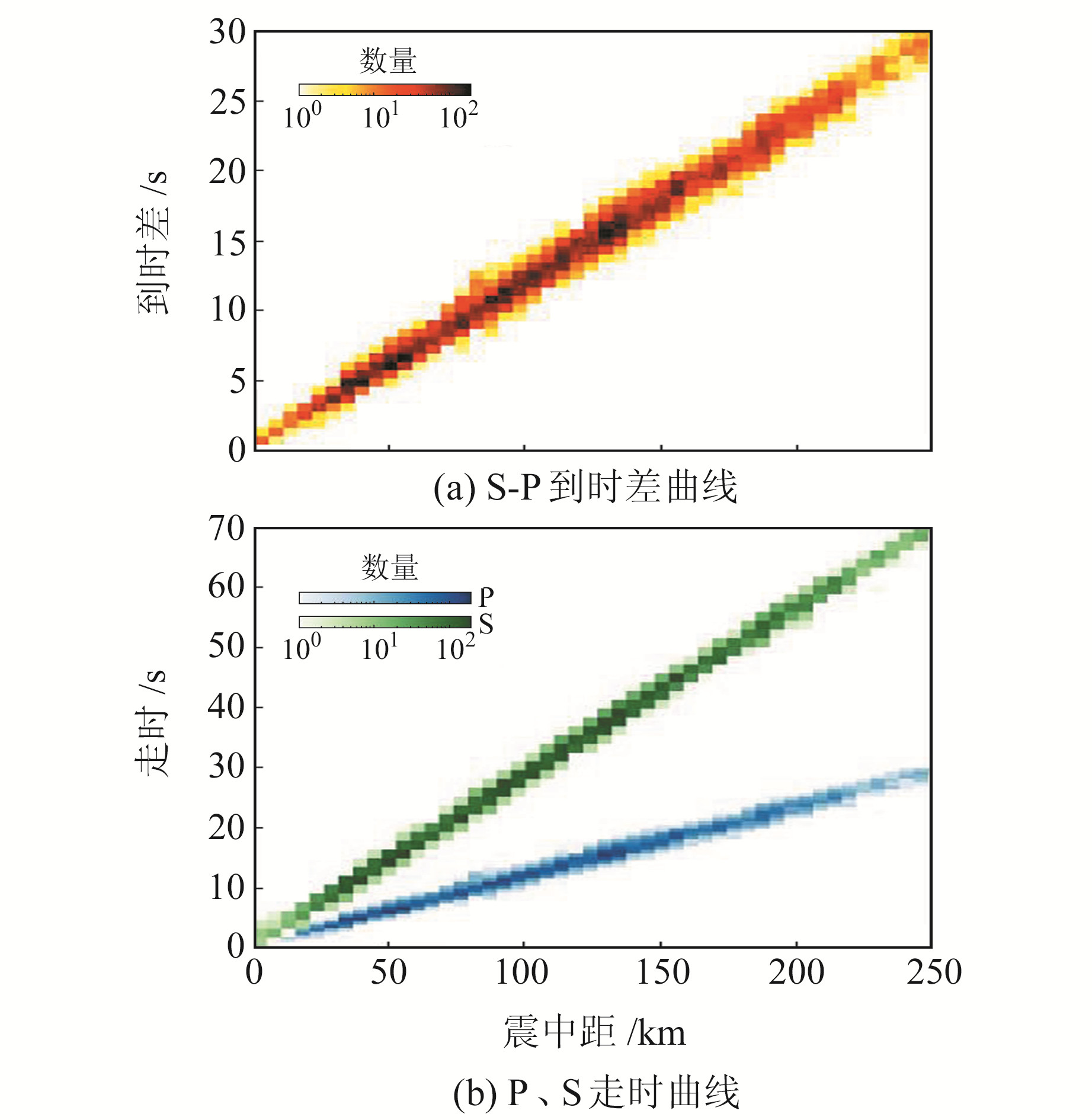
1 数据和方法 1.1 数据本文使用2013-01~2021-07湖北省区域地震台网50个地震台站记录到的1 198次近震(图 1)共8 779条事件波形,其中P波及S波震相到时由人工拾取,采样率为100 Hz,二者到时差及走时曲线见图 2。训练使用的最小地震震级为0.5,最大为5.1,大部分地震的震级小于2.5。
|
图 1 地震台站和震中分布 Fig. 1 Distribution of seismic stations and epicenters |
|
图 2 P波及S波震相曲线 Fig. 2 P-wave and S-wave phase curves |
PhaseNet是由Zhu等[3]基于医学图像分割领域的U-net开发的震相拾取模型。U-net是用于生物医学图像处理的深度神经网络方法,由4个下采样层和4个上采样层的U型网络结构组成[5]。地震学中的震相拾取是对地震波形的每个采样点进行三分类:P波震相、S波震相和噪声。PhaseNet使用北加州地震数据中心记录到的623 054条地震波形进行训练,网络训练参数数量为23 305。首先将30 s采样率100 Hz的三分量地震波形作为模型输入,对原始波形数据进行去均值和去趋势处理;然后去除每个分量的平均值后除以标准差,对数据进行振幅归一化预处理;最后给出P波、S波和噪声的概率分布。目前,该方法已应用于四川长宁[6]、云南漾濞[7]、美国加州[8]及意大利中亚平宁山脉[9]等地区的余震序列检测中。
Mousavi等[10]将全球大规模数据集STEAD作为训练集,基于Transformer建立地震检测和震相拾取网络。EQTransformer由17层编码层和3个8~10层解码层组成,编码层结合了CNN模型和RNN模型,并加入注意力机制以保留地震信号的局部和全局特征。使用解码层中的1个解码分支将编码层中获得的特征直接映射为检测地震信号的概率向量,另外2个解码器分支分别与P波震相和S波震相相关联,分别对应P波概率和S波概率。该训练集包含大约1 000 000条地震波形和300 000条噪声波形,网络训练参数数量大约为376 935,波形长度为1 min,采样率为100 Hz。拾取时需要对原始波形数据进行去趋势、振幅归一化及1~45 Hz带通滤波处理。EQTransformer包含EqT_model.h5(EqT1)和EqT_model2.h5(EqT2)2种模型,基于林学楷等[11]对2种模型的测试和意见,本文选取的EQTransformer模型为EqT_model.h5(EqT1)。将此模型应用于STEAD测试集时,小于0.5 s的残差(EQTransformer拾取的震相到时与人工目录对比)被认定为正确拾取。P波震相拾取的精确率为99.0%,召回率为99.0%;S波震相拾取的精确率为99.0%,召回率为96.0%。
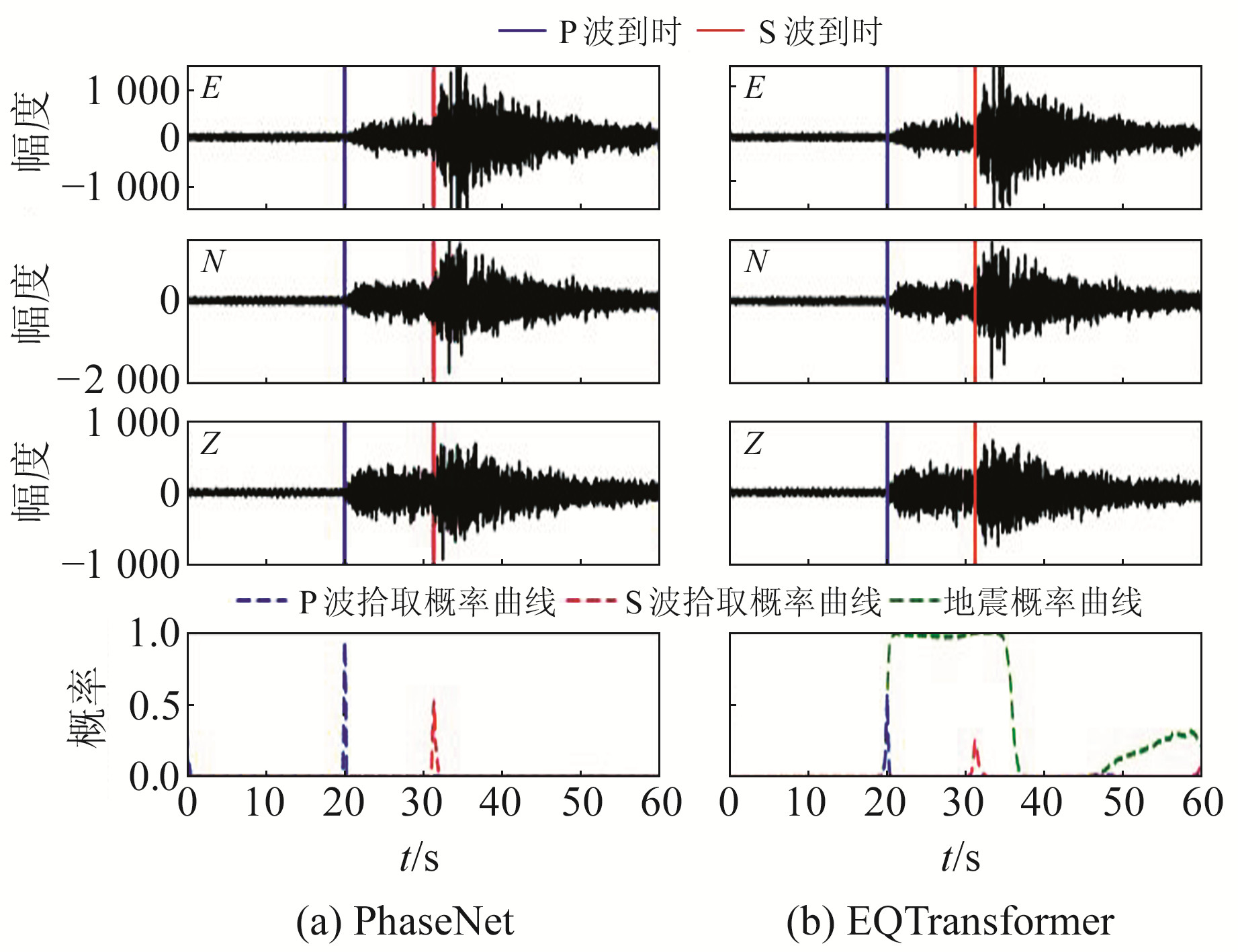
2 结果与对比分析图 3为PhaseNet和EQTransformer在数据集中的拾取示例,其中地震发震时刻为2016-05-27 13:27:11,震中位置为110.418°E、31.533°N,震级为1.5,震源深度10 km。以地震目录中的震相到时作为标准与自动拾取的震相到时进行比较,并利用精确率P、召回率R及F1值来评价模型的性能:
| $ P=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}} $ | (1) |
| $ R=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}} $ | (2) |
| $ F_1=2 \frac{P \times R}{P+R} $ | (3) |
|
图 3 PhaseNet和EQTransformer在数据集中的拾取示例 Fig. 3 Picking examples of PhaseNet and EQTransformer in the dataset |
式中,TP为真正例,即自动拾取的震相到时与人工目录中的震相到时相差小于预先设定的阈值;FP为假正例,即自动拾取的震相到时与人工目录中的震相到时相差高于阈值;FN为假反例,即人工目录中标注为震相但没有自动拾取到时。根据文献[4]将阈值设置为0.5 s。精确率P和召回率R是深度学习中常用的检测模型泛化能力的指标,F1值则将二者综合起来进行评价。
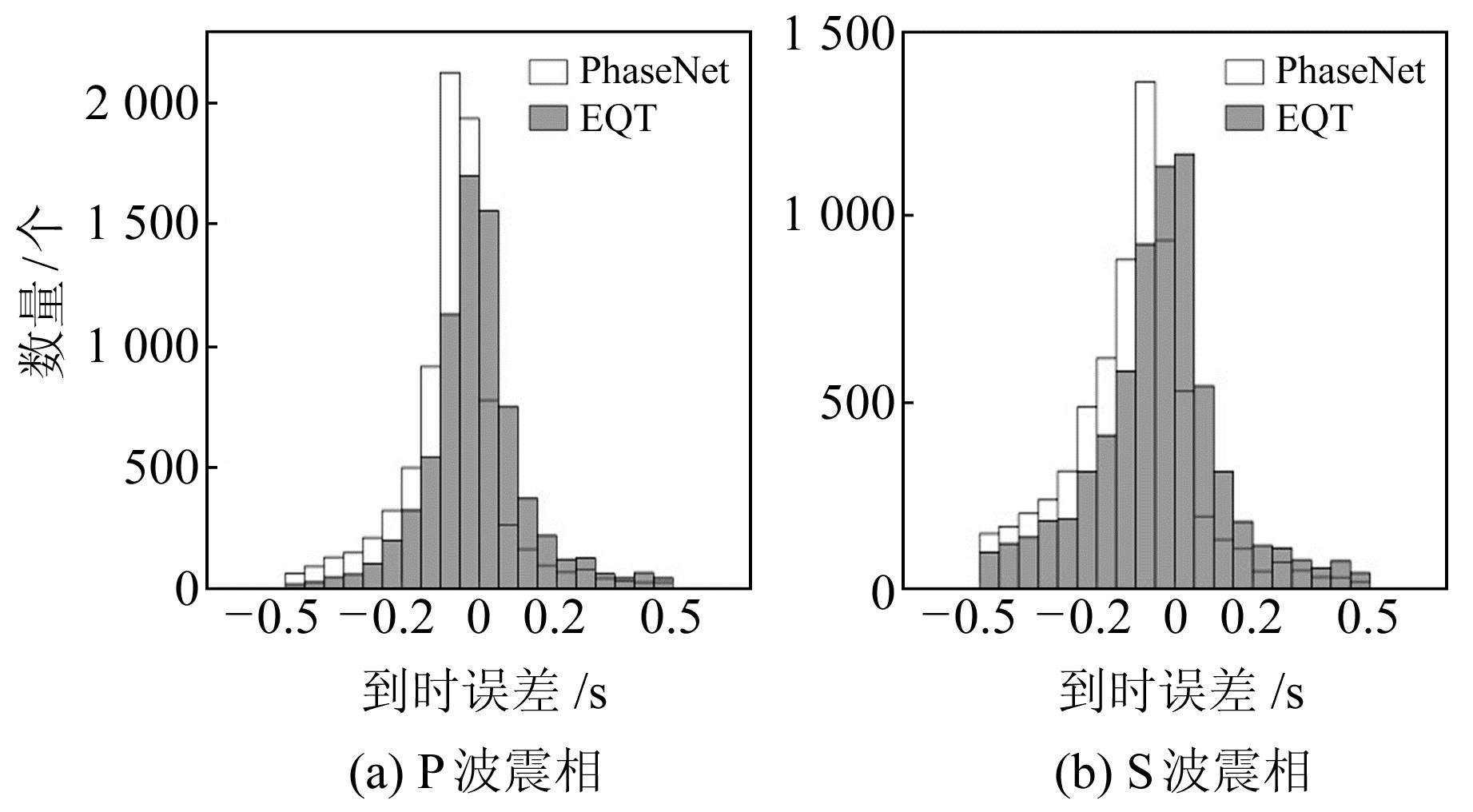
2.1 PhaseNet、EQTransformer模型测试结果本文使用2013-01~2021-07湖北测震台网50个地震台站记录到的1 198次近震作为数据集,共计8 779条事件波形,PhaseNet和EQTransformer输出的震相概率阈值均设置为0.1。图 4为2种模型拾取的P波和S波震相到时差值统计结果。由图可见,PhaseNet与人工拾取P波、S波震相的平均到时误差分别为-0.064 7 s和-0.102 8 s,绝对平均值分别为0.105 8 s和0.147 s,标准差分别为0.133 4 s和0.162 s;EQTransformer与人工拾取P波、S波震相的平均到时误差分别为-0.005 s和-0.039 s,绝对平均值分别为0.093 2 s和-0.039 s,标准差分别为0.134 6 s和0.172 s。
|
图 4 震相到时误差统计 Fig. 4 Statistics of arrival error of seismic phase |
为比较PhaseNet和EQTransformer在湖北测震台网的震相拾取效果,在不同的震相概率阈值下比较其精度P、召回率R和F1值(表 1)。由表可见,对于P波而言,PhaseNet具有良好的震相拾取能力,当震相概率阈值为0.1或0.3时,PhaseNet的召回率R均高于EQTransformer,震相拾取的F1值均超过0.9;EQTransformer拾取效果略差,当阈值为0.3时,F1值仅约为0.79,随着震相概率阈值的提高,EQTransformer的召回率R显著下降,F1值变化幅度大于PhaseNet,但精度高于PhaseNet。S波的2种模型拾取效果均差于P波,虽然PhaseNet的拾取精确率P低于EQTransformer,但随着概率阈值的提高,其召回率R明显高于EQTransformer,F1值也能保持在0.8左右,具有较为稳定的拾取表现。由此可知,PhaseNet具有更高的召回率或更完备的震相拾取,但误拾取率较高;EQTransformer虽然检测到的地震数量较少,但拾取精度相对较高。
|
|
表 1 PhaseNet和EQTransformer的P波及S波震相拾取结果 Tab. 1 P-wave and S-wave phase pickup results of PhaseNet and EQTransformer |
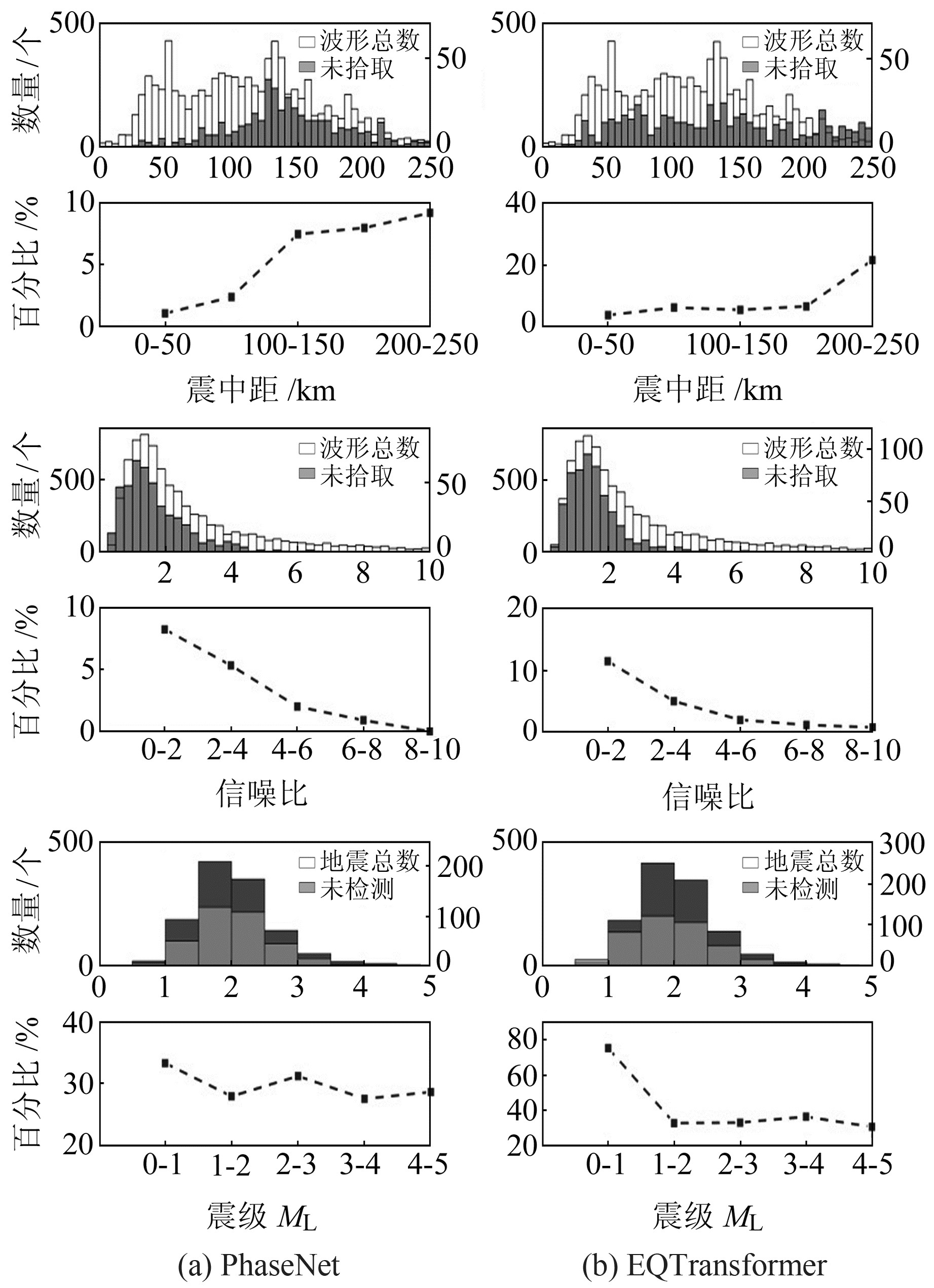
为获取更优化的模型,本文从震中距、震级、信噪比等方面分析PhaseNet与EQTransformer模型拾取精度的影响因素,其中PhaseNet和EQTransformer的震相概率阈值分别设置为0.1和0.3。图 5为事件波形数量和未拾取到震相的事件波形数量随震中距、震级和信噪比的变化情况。由图可见,数据集样本中90%以上的震中距分布在0~150 km之间,震级分布为1.0~2.5,信噪比分布为0~3。由图 5(a)可见,PhaseNet算法检测效果与震中距关联较强,震中距100 km以内未检测事件数量较少,而大于100 km未检测事件数量随震中距的增加而增加;信噪比与未检测事件数量占比呈负相关,虽然PhaseNet对低信噪比数据有相对较高的拾取率,但检测正确率仍然依赖于数据的信噪比;PhaseNet算法检测效果与震级关联不强。由图 5(b)可见,EQTransformer未检测到的事件数量占比趋于平稳,震中距大于200 km的占比有所提高;与PhaseNet检测结果相似,随着信噪比的增加,未检测事件的占比逐渐减小,说明2种算法检测效果与信噪比关系较大;虽然震相波形的数量占比趋于平稳,但0≤ML≤1范围内的地震占比较高,可能与该震级范围内的数据信噪比有关。
|
图 5 PhaseNet和EQTransformer未检测到事件波形的震中距、信噪比、震级统计 Fig. 5 Statistics of epicentral distance, signal-to-noise ratio, and magnitude changes in event waveforms not detected by PhaseNet and EQTransformer |
本文将国内外使用最为广泛的PhaseNet和EQTransformer模型应用于湖北地震监测台网中,对比分析2种模型的优缺点,结论如下:
1) PhaseNet的召回率高于EQTransformer,漏检率较低,但拾取到的震相数量远大于实际数量,可能是由于其训练过程中未涉及噪声数据集所致。EQTransformer能够提供更高的拾取精度,拾取到的错误震相更少,但会漏拾取更多的震相。当震相概率阈值为0.1或0.3时,PhaseNet的召回率高于EQTransformer,有可能检测到人工目录中不存在的震相到时[12],可以通过REAL等关联算法去除错误震相、关联出可靠地震,该方法已较好地应用于四川长宁、云南漾濞等地区的余震序列检测中[6-7, 13]。提高震相概率阈值后,2种模型的召回率R和精确率P都有所变化,EQTransformer的召回率R和精确率P的变化幅度大于PhaseNet。随着震相概率阈值的提高,EQTransformer拾取到的震相到时可靠性也随之提高,但可能会造成震相漏拾取。因此,选择一个合理的震相概率阈值显得尤为重要[14]。
在地震预警等实际应用中,召回率R比精确率P具有更高的优先级,因此PhaseNet模型更具优势,且应用场景更加广泛[15]。但是由于连续地震波形数据受噪声影响较大,PhaseNet所表现的召回率R和精确率P相较震相拾取可能偏低,因此需要在选取合适震相概率阈值的基础上进行地震关联、定位等处理进行弥补。对于自动编目,应适当提高精度、减少震相拾取误差,同时保证一定的查全能力,尽量减少人工审核的工作量。EQTransformer模型的召回率R较低,具有较高的精确率P,在实际使用时建议采用低阈值,在不降低精确率的基础上检测到更多震相。后续可结合模板匹配方法进一步扩大EQTransformer获得的地震目录数量。
2) PhaseNet模型检测效果与信噪比和震中距关联较强,与震级的关联性不大。随着信噪比的增加,检测到震相波形的数量占比逐渐增大,检测正确率变高[15]。当震中距小于100 km时,检测到震相波形数量较多;而超过100 km的震相波形数量逐渐减少,可能是因为信噪比随震中距的增大而减小[2]。EQTransformer受信噪比的影响较大,与震中距和震级的关联不强。随着信噪比的提高,检测到震相波形的数量占比逐渐降低。震中距大于200 km及震级为0≤ML≤1的未检测事件占比较大,可能跟训练数据集有关。EQTransformer使用STEAD数据集作为训练集,其中包含来自全球的1 000 000条地震波形以及300 000条噪声波形;PhaseNet使用NCEDC记录的623 054条波形进行训练。从数量上看,EQTransformer使用的数据量更大;从训练集的空间分布上看,STEAD数据集具有全球性,NCEDC数据集仅具有区域性。由此可知,数据是提高模型泛化能力的一个重要因素。
将已经训练好的模型应用于其他研究区域时,如果能够获得目标区域的历史数据,采用迁移学习的策略对模型权重参数进行重新训练,将会得到更好的检测和拾取效果。例如在训练数据集中增加震中距大于100 km、低信噪比的数据,并在训练过程中增加这些类别数据的权重,将有助于增强湖北区域的检测效果,提高地震目录的完整性。
| [1] |
杨旭, 李永华, 苏伟, 等. 基于优化参数的地震P、S波震相到时自动拾取及质量评估[J]. 地球物理学报, 2019, 62(11): 4 290-299 (Yang Xu, Li Yonghua, Su Wei, et al. Optimized Automatic Pickers and Quality Assessment: Application to Identification of Local and Regional P and S Wave Phases[J]. Chinese Journal of Geophysics, 2019, 62(11): 4 290-299)
(  0) 0) |
| [2] |
Ross Z E, Meier M A, Hauksson E. P Wave Arrival Picking and First-Motion Polarity Determination with Deep Learning[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(6): 5 120-5 129 DOI:10.1029/2017JB015251
(  0) 0) |
| [3] |
Zhu W Q, Beroza G C. PhaseNet: A Deep-Neural-Network-Based Seismic Arrival-Time Picking Method[J]. Geophysical Journal International, 2018, 216(1): 261-273
(  0) 0) |
| [4] |
Mousavi S M, Ellsworth W L, Zhu W Q, et al. Earthquake Transformer—An Attentive Deep-Learning Model for Simultaneous Earthquake Detection and Phase Picking[J]. Nature Communications, 2020, 11(1): 1-12 DOI:10.1038/s41467-019-13993-7
(  0) 0) |
| [5] |
Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation[M]. Cham: Springer International Publishing, 2015
(  0) 0) |
| [6] |
赵明, 唐淋, 陈石, 等. 基于深度学习到时拾取自动构建长宁地震前震目录[J]. 地球物理学报, 2021, 64(1): 54-66 (Zhao Ming, Tang Lin, Chen Shi, et al. Machine Learning Based Automatic Foreshock Catalog Building for the 2019 MS6.0 Changning, Sichuan Earthquake[J]. Chinese Journal of Geophysics, 2021, 64(1): 54-66)
(  0) 0) |
| [7] |
苏金波, 刘敏, 张云鹏, 等. 基于深度学习构建2021年5月21日云南漾濞MS6.4地震序列高分辨率地震目录[J]. 地球物理学报, 2021, 64(8): 2 647-2 656 (Su Jinbo, Liu Min, Zhang Yunpeng, et al. High Resolution Earthquake Catalog Building for the 21 May 2021 Yangbi, Yunnan, MS6.4 Earthquake Sequence Using Deep-Learning Phase Picker[J]. Chinese Journal of Geophysics, 2021, 64(8): 2 647-2 656)
(  0) 0) |
| [8] |
Liu M, Zhang M, Zhu W Q, et al. Rapid Characterization of the July 2019 Ridgecrest, California, Earthquake Sequence from Raw Seismic Data Using Machine-Learning Phase Picker[J]. Geophysical Research Letters, 2020, 47(4)
(  0) 0) |
| [9] |
Zhang X, Zhang M, Tian X. Real-Time Earthquake Early Warning with Deep Learning: Application to the 2016 M 6.0 Central Apennines, Italy Earthquake[J]. Geophysical Research Letters, 2021, 48(5)
(  0) 0) |
| [10] |
Mousavi S M, Sheng Y X, Zhu W Q, et al. Stanford Earthquake Dataset(STEAD): A Global Data Set of Seismic Signals for AI[J]. IEEE Access, 2019, 7: 179 464-179 476 DOI:10.1109/ACCESS.2019.2947848
(  0) 0) |
| [11] |
林学楷, 许才军. 深度学习驱动的地震目录构建: PhaseNet和EqT模型的对比与评估[J]. 武汉大学学报: 信息科学版, 2022, 47(6): 855-865 (Lin Xuekai, Xu Caijun. Deep-Learning-Empowered Earthquake Catalog Building: Comparison and Evaluation of PhaseNet and EqT Models[J]. Geomatics and Information Science of Wuhan University, 2022, 47(6): 855-865)
(  0) 0) |
| [12] |
Jiang C, Fang L H, Fan L P, et al. Comparison of the Earthquake Detection Abilities of PhaseNet and EQTransformer with the Yangbi and Maduo Earthquakes[J]. Earthquake Science, 2021(5): 425-435
(  0) 0) |
| [13] |
Zhang M, Ellsworth W L, Beroza G C. Rapid Earthquake Association and Location[J]. Seismological Research Letters, 2019, 90(6): 2 276-2 284
(  0) 0) |
| [14] |
周本伟, 范莉苹, 张龙, 等. 利用卷积神经网络检测地震的方法与优化[J]. 地震学报, 2020, 42(6): 669-683 (Zhou Benwei, Fan Liping, Zhang Long, et al. Earthquake Detection Using Convolutional Neural Network and Its Optimization[J]. Acta Seismologica Sinica, 2020, 42(6): 669-683)
(  0) 0) |
| [15] |
赵明, 陈石. 基于深度学习的地震检测模型在区域台网的泛化性研究[J]. 地震, 2021, 41(1): 166-179 (Zhao Ming, Chen Shi. The Generalization Ability Research of Deep Learning Algorithm in Seismic Phase Detection of Regional Seismic Network[J]. Earthquake, 2021, 41(1): 166-179)
(  0) 0) |
2. Key Laboratory of Earthquake Geodesy, CEA, 40 Hongshance Road, Wuhan 430071, China
 2023, Vol. 43
2023, Vol. 43


