近年来,半参数模型在测绘等领域得到广泛应用[1-4]。补偿最小二乘估计是半参数模型求解参数最常用的方法,正则参数和正则矩阵的确定是其中的2个关键问题。常用的正则参数确定方法有CV法、GCV法、遗传算法和L曲线法等[5],但上述方法在应用领域表现出一定的局限性:如GCV法可能出现迭代不收敛问题;L曲线法能够搜索到曲率最大的点从而确定正则参数,但过于依赖数据拟合精度等。为解决上述问题,王乐洋等[6]采用U曲线法确定地震同震滑动分布,反演正则化参数,后又提出改进的折中相交曲线(EI)法[7-8]。目前,针对正则参数确定方法的研究已取得丰硕成果,但针对正则矩阵的研究相对较少,鲜有学者将半参数模型引入地学分析中。时间序列法和三次样条函数法是构建正则矩阵的最常用方法[1-2],但时间序列法要求相邻时刻信号的变化不能太大,且缺乏严密的数学依据;三次样条函数法具有严密的数学依据,但要求信号具有严格的连续性,这一条件在很多领域都难以满足。明锋等[9]、张俊等[10]将半参数模型引入地壳形变分析中,取得了初步成果。但由于地壳运动形变具有特殊性和复杂性,若采用常见的时间序列法或样条函数法确定模型解算的正则矩阵,会面临异常观测影响难以消除等问题[10]。
本文尝试将信息扩散函数引入半参数估计中,以主模型(参数化模型)的最小二乘估计标准化残差为信号,利用信号的信息扩散函数估计值构建正则矩阵,并应用于地壳形变分析中。对中国大陆华北块体GPS速度场进行半参数地壳形变拟合分析,结果表明,相比于时间序列法,新方法具有更优的拟合精度。
1 半参数模型及其补偿最小二乘估计半参数模型的一般表达式为[1]:
| $ \boldsymbol{L}=\boldsymbol{B} \boldsymbol{X}+\boldsymbol{S}+\mathit{\pmb{\Delta}} $ | (1) |
式中,L为由n个观测值构成的观测向量;B为参数化后的系数矩阵;X为待求未知参数,其估值记为
将式(1)改写为误差方程:
| $ \boldsymbol{V}=\boldsymbol{B} \hat{\boldsymbol{X}}+\hat{\boldsymbol{S}}-\boldsymbol{L} $ | (2) |
根据极小化过程求解参数及非参数:
| $ \boldsymbol{V}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{V}+a \hat{\boldsymbol{S}}^{\mathrm{T}} \boldsymbol{R} \hat{\boldsymbol{S}}=\min $ | (3) |
式中,P为观测值权阵,R为正则矩阵,a∈[0, +∞]称为正则参数。式(3)为补偿最小二乘准则,其中,“补偿”通过
| $ \left\{\begin{array}{l} \hat{\boldsymbol{S}}=(\boldsymbol{M}+a \boldsymbol{R})^{-1} \boldsymbol{M} \boldsymbol{L} \\ \hat{\boldsymbol{X}}=\boldsymbol{N}^{-1} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{P}(\boldsymbol{L}-\hat{\boldsymbol{S}}) \\ \boldsymbol{M}=\boldsymbol{P}-\boldsymbol{P B} \boldsymbol{N}^{-1} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{P} \\ \boldsymbol{N}=\boldsymbol{B}^{\mathrm{T}} \boldsymbol{P B} \end{array}\right. $ | (4) |
设W为来自母体K的样本,f(x)为对应的概率密度函数。由于W样本数量不足,f(x)一般很难被精确确定,此时,W对K非完备[11]。王新洲[11]、黄崇福[12]指出,上述缺陷可通过增加样本数量进行改善。W从非完备趋向于完备的过程中,每一个样本点都必然会充当其周围未出现样本点的代表。若设wi的观测值为yi,则在区域完备化的过程中,W在yi点的信息被其周围样本点分享,同时yi也会获取其周围样本点信息。这种相互传递或分享信息的能力与yi点“周围的程度”有关。若记yi点自身信息量为1,则其周围的点从yi处获取的信息量介于0到1之间,这种样本点将其信息向其周围样本点扩散的过程称为信息扩散。
2.2 信息扩散估计设W={w1, w2, w3, …, wn}为来自母体K的知识样本,Y为W的基础论域,设
若设Δn>0为常数,则母体K的概率密度函数f(y)扩散估计为:
| $ f(y)=\frac{1}{n \mathit{\Delta}_n} \sum\limits_{i=1}^n \mu\left[\mathit{\Phi}\left(\frac{y-y_i}{\mathit{\Delta}_n}\right)\right] $ | (5) |
式中,μ(·)为定义在(-∞,+∞)上的一个波雷尔可测函数,称为扩散函数;Δn为窗宽,是信息扩散方法中获得概率密度函数的一项关键元素。为寻找最优窗宽,解决信息扩散估计的难题,常用的方法有经验法、交错验证法、插入法等。
2.3 信息扩散函数及窗宽确定由式(5)可知,确定信息扩散函数μ(·)的具体形式是实现信息扩散估计的关键[11]。假定母体服从正态分布,则可根据分子扩散理论推导出μ(·)为[11]:
| $ \mu(x)=\frac{1}{\sigma \sqrt{2 \pi}} \exp \left(-\frac{x^2}{2 \sigma^2}\right) $ | (6) |
将式(6)代入式(5),可得母体的信息扩散估计:
| $ f(y)=\frac{1}{n h \sqrt{2 \pi}} \sum\limits_{i=1}^n \exp \left(-\frac{\left(y-y_i\right)^2}{2 h^2}\right) $ | (7) |
式中,h=σΔn为经验标准窗宽,可根据两点择近原则确定[11]。
为顾及W的随机性,采用平均距离:
| $ d=\frac{b-\alpha}{n-1} $ | (8) |
为了在最不利的情况下也能使两点择近原则成立,使
| $ \begin{gathered} 1+\exp \left(-\frac{d^2}{2 h^2}\right)=\exp \left(-\frac{d^2}{2 h^2}\right)+ \\ 2 \sum\limits_{i=1}^h \exp \left[-\frac{(i+1)^2 d^2}{2 h^2}\right] \end{gathered} $ | (9) |
令
| $ y=\exp \left(-\frac{d^2}{2 h^2}\right) $ | (10) |
| $ \mathit{\Psi}(y)=y^4+y^9+y^{16}+\cdots+y^{(k+1)^2}-\frac{1}{2} $ | (11) |
可得:
| $ h=\frac{\alpha(b-a)}{n-1} $ | (12) |
式中,
早期基于欧拉矢量法的刚性地壳运动模型不考虑块体内部形变[13],但事实上,地壳不是绝对刚性体,地壳运动时,其内部不可避免地存在不同程度的不规则形变。本世纪初提出的整体旋转与均匀应变模型REHSM[14]为解决板内形变问题提供了一种可行思路,但该模型假定块体内部形变均匀变化,存在局限性。张俊等[10]提出采用半参数模型对块体运动的整体旋转与均匀应变模型进行精化,进一步优化了地壳形变分析的REHSM模型。本文以REHSM为主模型构建半参数地壳形变分析模型[14],其形式为:
| $ \begin{array}{r} {\left[\begin{array}{l} \boldsymbol{L}_e \\ \boldsymbol{L}_n \end{array}\right]=\left[\begin{array}{ccc} -r \cos \lambda \sin \varphi & -r \sin \lambda \sin \varphi & r \cos \varphi \\ r \sin \lambda & -r \cos \lambda & 0 \end{array}\right]\left[\begin{array}{l} \omega_x \\ \omega_y \\ \omega_z \end{array}\right]+} \\ {\left[\begin{array}{cc} \varepsilon_{e e} & \varepsilon_{e n} \\ \varepsilon_{e n} & \varepsilon_{n n} \end{array}\right]\left[\begin{array}{c} r\left(\lambda-\lambda_0\right) \cos \varphi \\ r\left(\varphi-\varphi_0\right) \end{array}\right]+\left[\begin{array}{l} \boldsymbol{S}_e \\ \boldsymbol{S}_n \end{array}\right]+\left[\begin{array}{l} \mathit{\pmb{\Delta}}_e \\ \mathit{\pmb{\Delta}}_n \end{array}\right](13)} \end{array} $ | (13) |
式中,Le和Ln分别为地壳速度场在东西方向和南北方向上的速度分量;ωx、ωy、ωz为欧拉矢量在3个坐标轴上的分量;εee、εen、εnn为3个均匀应变参数;Se和Sn为运动速率在东西方向和南北方向上的补偿项,对照式(1)可知,此项正是半参数模型中的非参数向量。
3.2 利用信息扩散函数构建正则矩阵在不同的应用领域应当采用不同的方法合理确定正则矩阵。但目前已有成果大多直接采用时间序列法或样条函数法构建正则矩阵,未考虑其适用性,缺乏物理解释性,且对异常数据影响的抵抗性也较差。本文针对地壳形变,首先利用研究区域所属板块的平均欧拉矢量对站点速率进行中心化处理,然后将中心化后的速率(即去趋势项后的剩余速率)作为信号,最后利用信息扩散函数构建正则矩阵。具体形式为:
| $ f\left(v_i\right)=\frac{1}{n h \sqrt{2 \pi}} \sum\limits_{j=1}^n \exp \left(-\frac{\left(v_i-v_j\right)^2}{2 h^2}\right) $ | (14) |
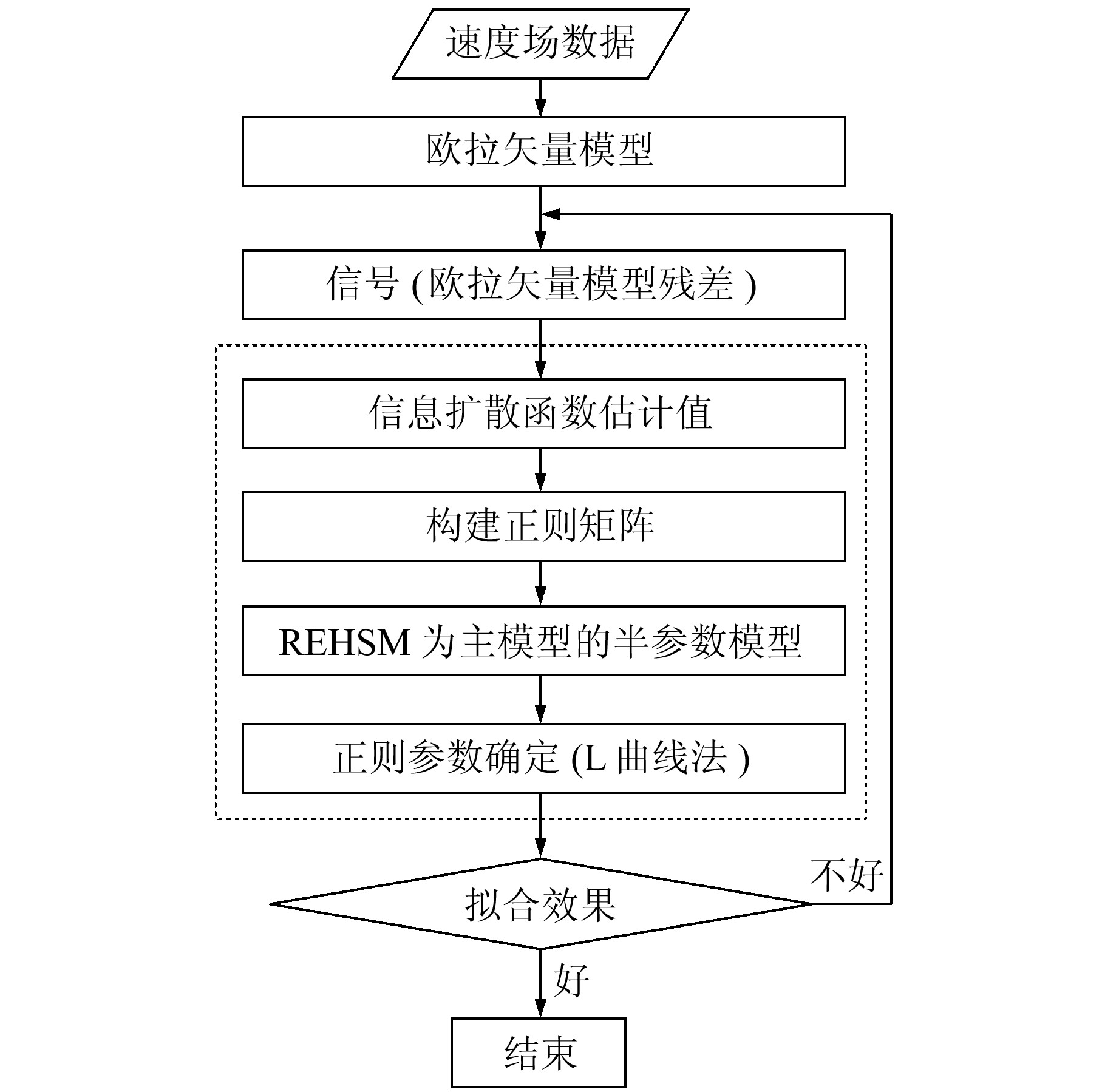
式中,vi和vj分别为仅保留式(13)右边第一项(即欧拉矢量模型)后,利用最小二乘估计获得的欧拉矢量对第i和第j个站点进行中心化后的剩余速率;f(·)为利用中心化速率计算的站点信息扩散估计值。取正则矩阵的主对角元素R(ii)=f(vi),i=1, 2, …, n。利用本文方法进行地壳形变分析的具体流程如图 1所示。
|
图 1 地壳形变分析流程 Fig. 1 Flow chart of crustal deformation analysis |
在111°~20°E、33°~42°N范围内以1°×1°的格网密度(共100个测站点)按照REHSM模型模拟地壳运动的速度场,模拟的欧拉旋转参数和应变参数见表 1。在上述数据的基础上,模拟服从正态分布N(0, 0.52)的偶然误差后得到速度场观测值。为验证本文方法的稳健性,随机选取10个测站点,在测站速度观测值上模拟5倍误差的粗差。为方便描述,将模拟粗差后的测站称为异常测站。采用4种方案对模拟速度场数据进行拟合分析。方案1:采用欧拉矢量法对100个站点(包括10个异常测站,下同)的速度场进行拟合分析;方案2:采用REHSM对100个站点的速度场进行拟合分析;方案3:采用式(13)给出的半参数模型对100个站点的速度场进行拟合分析,正则矩阵采用时间序列法确定,正则参数a由L曲线法确定;方案4:采用式(13)给出的半参数模型对100个站点的速度场进行拟合分析,正则矩阵采用式(14)给定的信息扩散函数估值确定,正则参数a由L曲线法确定。相关拟合结果见表 1。
|
|
表 1 欧拉运动参数与应变参数比较 Tab. 1 Comparison of Euler motion parameters and strain parameters |
由表 1可见,方案1的RMSE略大,说明不顾及板内形变的传统欧拉矢量法不符合地壳运动的实际情况,且不具备异常测站的处理能力。方案2与方案1的RMSE相差不大,原因是虽然REHSM考虑了板内形变,但其假设形变均匀,具有一定的局限性。由于本文在每个测站上模拟的偶然误差以及10个服从正态分布的大粗差都不符合均匀应变假设,因此方案2与方案1一样,也不具备异常测站处理能力。方案3的RMSE最大,因为该方案除了不满足均匀假设条件外,也不满足时间序列法确定正则矩阵对形变连续性、光滑性和周期性等要求。方案4的拟合精度明显提高,其拟合的参数结果与模拟真值非常接近,说明利用信息扩散函数确定正则矩阵不仅对偏离主模型REHSM的地壳运动具有补偿作用,还能使平差系统具备良好的抗粗差能力。
4.2 实例验证及分析采用与模拟算例相同的处理方案,对文献[13]中给出的ITRF97参考框架下分布于华北块体的93个GPS站点的地壳运动速度场数据进行拟合分析,表 2为各测站速率在东西方向和南北方向上拟合残差的最大值Ve-max、Vn-max以及所有站点整体拟合残差的标准差σΔV。
|
|
表 2 GPS速度场拟合情况 Tab. 2 GPS velocity field fitting |
由表 2可见,不同方案计算的欧拉运动参数不同,这是因为各种方案对板内形变的描述方法不同(方案1未顾及板内形变),但各种方案给出的华北块体以百万年为尺度的平均旋转角速度却基本相同,说明华北块体地壳运动确实以刚性运动为主,内部形变并不影响其整体刚性运动趋势[13]。从各方案给出的速率残差最大值和残差标准差统计情况来看,方案1的拟合结果最差,主要原因是方案1没有考虑板内形变;方案2的拟合结果优于方案1,但差于方案3和方案4,这是因为方案2假设板内形变均匀,这与华北区域复杂的构造形变情况不符;方案3和方案4利用半参数模型对方案2进行了优化,在假定板内形变均匀应变的基础上,引入非参数对偏离均匀应变的部分进行了补偿。其中方案4优于方案3,这是因为2种方案在参数估计时采用的正则矩阵不同:方案3采用时间序列法确定模型解算的正则矩阵,其基本前提是假定形变信号具有连续性和一定的周期性。尽管文献[10]对地壳运动可能具有的周期运动进行了解释,但地壳形变的连续性假设无法保证;而方案4将方案1中的速率标准化残差(即去趋势项后的剩余速率)作为信号,采用信号的信息扩散函数估值构建正则矩阵,即根据剩余速率本体信息构建正则矩阵,对形变是否连续以及是否具有周期性均无要求。同时信息扩散函数相当于事先确定了信号的分布,使得参数估计具有较好的稳健性。
5 结语本文针对正则矩阵确定方法进行研究,将信息扩散函数引入地壳形变分析的半参数模型估计中。华北块体的实测GPS速度场拟合分析结果表明,利用信息扩散函数构建正则矩阵可以极大地提高半参数地壳形变分析结果的精度和准确度,为半参数模型正则矩阵确定和地壳形变分析提供了新的研究思路。
需要指出的是,本文方法并非仅适用于地壳形变分析,而是为半参数模型解算提供了一种通用的正则矩阵确定方法。“信号”的种类可以多种多样,当“信号”为多量纲时,可首先对“信号”作标准化处理,然后再利用信息扩散函数计算正则矩阵元素。未来可尝试配合采用U曲线法等不同的正则参数确定方法,进一步阐述本文正则矩阵确定方法的应用效果。
| [1] |
孙海燕, 吴云. 半参数回归与模型精化[J]. 武汉大学学报: 信息科学版, 2002, 27(2): 172-174 (Sun Haiyan, Wu Yun. Semiparametric Regression and Model Refining[J]. Geomatics and Information Science of Wuhan University, 2002, 27(2): 172-174)
(  0) 0) |
| [2] |
丁士俊, 张松林, 张洪波, 等. 半参数模型稳健估计及其应用[J]. 测绘科学技术学报, 2007, 24(1): 26-29 (Ding Shijun, Zhang Songlin, Zhang Hongbo, et al. Robust Estimate and Its Applications for Semiparametric Models[J]. Journal of Geomatics Science and Technology, 2007, 24(1): 26-29)
(  0) 0) |
| [3] |
邱封钦, 潘雄, 罗小敏, 等. 综合半参数核估计和自回归补偿的全球电离层总电子含量预报模型[J]. 地球物理学报, 2021, 64(9): 3 021-3 029 (Qiu Fengqin, Pan Xiong, Luo Xiaomin, et al. Global Ionospheric TEC Prediction Model Integrated with Semiparametric Kernel Estimation and Autoregressive Compensation[J]. Chinese Journal of Geophysics, 2021, 64(9): 3 021-3 029)
(  0) 0) |
| [4] |
Wang L Y, Xiong L Y, Chen T. Penalized Total Least Squares Method for Dealing with Systematic Errors in Partial EIV Model and Its Precision Estimation[J]. Geodesy and Geodynamics, 2021, 12(4): 249-257 DOI:10.1016/j.geog.2021.04.001
(  0) 0) |
| [5] |
王振杰, 欧吉坤, 曲国庆, 等. 用L-曲线法确定半参数模型中的平滑因子[J]. 武汉大学学报: 信息科学版, 2004, 29(7): 651-653 (Wang Zhenjie, Ou Jikun, Qu Guoqing, et al. Determining the Smoothing Parameter in Semi-Parametric Model Using L-Curve Method[J]. Geomatics and Information Science of Wuhan University, 2004, 29(7): 651-653)
(  0) 0) |
| [6] |
王乐洋, 赵雄. 用U曲线法确定地震同震滑动分布反演正则化参数[J]. 大地测量与地球动力学, 2018, 38(11): 1 196-1 201 (Wang Leyang, Zhao Xiong. Using U Curve Method to Determine the Regularization Parameters of Coseismic Earthquake Slip Distribution Inversion[J]. Journal of Geodesy and Geodynamics, 2018, 38(11): 1 196-1 201)
(  0) 0) |
| [7] |
王乐洋, 赵雄. 地震同震滑动分布反演平滑因子的确定[J]. 测绘学报, 2018, 47(12): 1 571-1 580 (Wang Leyang, Zhao Xiong. Determination of Smoothing Factor for the Co-Seismic Slip Distribution Inversion[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(12): 1 571-1 580)
(  0) 0) |
| [8] |
Wang L Y, Gu W W. A-Optimal Design Method to Determine the Regularization Parameter of Coseismic Slip Distribution Inversion[J]. Geophysical Journal International, 2020, 221(1): 440-450 DOI:10.1093/gji/ggaa030
(  0) 0) |
| [9] |
明锋, 柴洪洲. 由GPS资料讨论中国大陆块体运动与应变模型的建立及检验[J]. 地球物理学报, 2009, 52(8): 1 993-2 000 (Ming Feng, Chai Hongzhou. The Foundation of Chinese Mainland Blocks Movement and Strain Model and Its Test Based on the GPS Data[J]. Chinese Journal of Geophysics, 2009, 52(8): 1 993-2 000)
(  0) 0) |
| [10] |
张俊, 李屹旭, 张显云. 利用半参数模型精化REHSM和RELSM两种弹性地壳运动模型[J]. 大地测量与地球动力学, 2018, 38(4): 362-365 (Zhang Jun, Li Yixu, Zhang Xianyun. REHSM and RELSM Improved by Semi-Parametric Model[J]. Journal of Geodesy and Geodynamics, 2018, 38(4): 362-365)
(  0) 0) |
| [11] |
王新洲. 基于信息扩散原理的估计理论、方法及其抗差性[J]. 武汉测绘科技大学学报, 1999, 24(3): 240-244 (Wang Xinzhou. The Theory, Method and Robustness of the Parameter Estimation Based on the Principle of Information Spread[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1999, 24(3): 240-244)
(  0) 0) |
| [12] |
黄崇福. 信息扩散原理与计算思维及其在地震工程中的应用[D]. 北京: 北京师范大学, 1992 (Huang Chongfu. The Principle of Information Diffusion and Thought Computation and Their Applications in Earthquake Engineering[D]. Beijing: Beijing Normal University, 1992)
(  0) 0) |
| [13] |
Wang Q, Zhang P Z, Freymueller J T, et al. Present-Day Crustal Deformation in China Constrained by Global Positioning System Measurements[J]. Science, 2001, 294(5 542): 574-577
(  0) 0) |
| [14] |
李延兴, 黄珹, 胡新康, 等. 板内块体的刚性弹塑性运动模型与中国大陆主要块体的应变状态[J]. 地震学报, 2001, 23(6): 565-572 (Li Yanxing, Huang Cheng, Hu Xinkang, et al. The Rigid and Elastic-Plastic Model of the Blocks in Intro-Plate and Strain Status of Principal Blocks in the Continent of China[J]. Acta Seismologica Sinica, 2001, 23(6): 565-572)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


