球谐函数是拉普拉斯方程在球坐标系下解的角度部分，球谐函数中与(余)纬度有关的部分称为缔合勒让德函数(associated legendre functions, ALFs)。在某些研究领域中需要计算出几千阶甚至几万阶的完全规格化缔合勒让德函数(fnALFs)数值。例如，当前采用的地球引力位球谐展开模型已展开至几千阶^[1-2]；在研究负荷形变时，基岩和冰盖的球谐级数展开模型已达10 800阶^[3]；残余地形模型(RTM)的球谐级数已展开至43 200阶^[4]。而在实际计算过程中，只能通过一些递推公式来计算fnALFs数值^[5-6]，其中标准向前按列/行递推公式在计算过程中很容易出现溢出现象^[7]，因此无论是在计算精度还是执行效率上，列式递推公式和跨阶次递推公式都明显优于标准向前按列/行递推公式^[8-9]。

除了计算fnALFs本身数值外，有时还需要计算其相对(余)纬度各阶导数的数值^[10-11]以及在指定区间上的定积分^[12-14]。为了拓展fnALFs计算的适用性和普适性，Fukushima^[10]提出拓展浮点数方法(X-数方法)，极大扩展了计算机数值的表示范围，且可应用于fnALFs的一、二、三阶导数及积分的递推计算中；Wittwer等^[15]提出扩充数域方法，无需改变递推公式，通过为每个浮点数的指数开辟单独存储空间，从而扩展计算机最大值和非零微小数值的表示范围，但该方法会严重影响计算效率；刘缵武等^[16]在基本递推公式中插入压缩因子，提出超高阶球谐级数式的复合Horner求和技术，可避免出现溢出现象；Gruber等^[17]提出傅里叶级数展开算法。上述研究都为fnALFs的计算提供了新途径。

列式递推公式是指将$\boldsymbol{P}_n^m(x) $表示为$\boldsymbol{P}_{n-1}^{m-1}(x) 、\boldsymbol{P}_{n-1}^m(x) \text { 和 } \boldsymbol{P}_{n-1}^{m+1}(x) $的线性组合，若这3个相邻元素中的某一个不存在，则将其设置为0。Belikov^[18]提出的列式递推公式是fnALFs的常用算法，但递推至3 100阶时会出现溢出现象。若将Belikov^[18]提出的列式递推公式完全规格化，则可至少直接递推至15 000阶。本文首先给出Belikov列式递推公式的证明，然后提出3种新的列式递推公式，并对4种列式递推公式的适用性和普适性进行分析。

1 缔合勒让德函数(ALFs)

令$x=\cos \theta 、y=\sin \theta \text { 且 } \theta \in[0, \pi] $，则ALFs为^[5-6]：

$ \begin{aligned} & \boldsymbol{P}_n(x)=\frac{1}{2^n n !} \frac{\mathrm{d}^n\left(x^2-1\right)^n}{\mathrm{~d} x^n} \\ & \boldsymbol{P}_n^m(x)=y^m \frac{\mathrm{d}^m \boldsymbol{P}_n(x)}{\mathrm{d} x^m} \end{aligned} $

(1)

式中，n和m分别为阶和次，均为0和正整数，且m≤n。显然，$\boldsymbol{P}_n^0(x)=\boldsymbol{P}_n(x) $。

基本递推公式为^[5-6]：

$ \boldsymbol{P}_n^{n-1}(x)=(2 n-1) x \boldsymbol{P}_{n-1}^{n-1}(x) $

(2)

$ \boldsymbol{P}_n^n(x)=(2 n-1) y \boldsymbol{P}_{n-1}^{n-1}(x) $

(3)

$ \boldsymbol{P}_{n+1}^m(x)=\boldsymbol{P}_{n-1}^m(x)+(2 n+1) y \boldsymbol{P}_n^{m-1}(x) $

(4)

$ (n-m+1) y \boldsymbol{P}_n^{m-1}(x)=x \boldsymbol{P}_n^m(x)-\boldsymbol{P}_{n-1}^m(x) $

(5)

$ y \boldsymbol{P}_n^{m+1}(x)=(n+m) \boldsymbol{P}_{n-1}^m(x)-(n-m) x \boldsymbol{P}_n^m(x) $

(6)

2 不完整类型的列式递推公式 2.1 各种类型列式递推公式的证明

联立式(4)~(6)可得：

$ \begin{aligned} & \text { eq. (4) } \times(2 n+2)+\text { eq. (5) } \times \\ & (3 n+m+2)+\text { eq. (6) } \end{aligned} $

(7)

简化得：

$ \begin{aligned} & (2 n+2) \boldsymbol{P}_{n+1}^m(x)=(n+m)(n+m+1) \cdot \\ & y \boldsymbol{P}_n^{m-1}(x)+(2 n+2 m+2) x \boldsymbol{P}_n^m(x)-y \boldsymbol{P}_n^{m+1}(x) \end{aligned} $

(8)

将式(8)中的阶数降1，则有：

$ \begin{gathered} (2 n) \boldsymbol{P}_n^m(x)=(n+m-1)(n+m) y \boldsymbol{P}_{n-1}^{m-1}(x)+ \\ 2(n+m) x \boldsymbol{P}_{n-1}^m(x)-y \boldsymbol{P}_{n-1}^{m+1}(x) \end{gathered} $

(9)

式(9)即为第1种类型的列式递推公式，要求次满足1≤m≤(n－2)。

将式(4)与式(5)相加并将其阶数降1，则有：

$ \boldsymbol{P}_n^m(x)=(n+m-1) y \boldsymbol{P}_{n-1}^{m-1}(x)+x \boldsymbol{P}_{n-1}^m(x) $

(10)

式(10)即为第2种类型的列式递推公式，要求次满足1≤m≤(n－1)。

联立式(4)~(6)：

$ \begin{aligned} & \text { eq. (4) } \times(n-m+1)+ \\ & \text { eq. }(5) \times(2 n+1)+\text { eq. }(6) \end{aligned} $

(11)

简化得：

$ \begin{gathered} (n-m+1) \boldsymbol{P}_{n+1}^m(x)= \\ (n+m+1) x \boldsymbol{P}_n^m(x)-y \boldsymbol{P}_n^{m+1}(x) \end{gathered} $

(12)

将式(12)中的阶数降1，则有：

$ \begin{gathered} (n-m) \boldsymbol{P}_n^m(x)= \\ (n+m) x \boldsymbol{P}_{n-1}^m(x)-y \boldsymbol{P}_{n-1}^{m+1}(x) \end{gathered} $

(13)

式(13)即为第3种类型的列式递推公式，要求次满足0≤m≤(n－2)。

标准向前按行递推公式为^[19]：

$ \begin{gathered} (n-m)(n+m-1) y \boldsymbol{P}_{n-1}^{m-1}(x)= \\ (2 m) x \boldsymbol{P}_{n-1}^m(x)-y \boldsymbol{P}_{n-1}^{m+1}(x) \end{gathered} $

(14)

联立式(10)、(14)可得：

$ \text { eq. (10) } \times 2 m-\text { eq. (14) } $

(15)

简化得：

$ \begin{gathered} (2 m) \boldsymbol{P}_n^m(x)=(n+m)(n+m-1) \cdot \\ y \boldsymbol{P}_{n-1}^{m-1}(x)+y \boldsymbol{P}_{n-1}^{m+1}(x) \end{gathered} $

(16)

式(16)即为第4种类型的列式递推公式，要求次满足1≤m≤(n－2)。

2.2 各种类型的列式递推公式中次的拓展

根据式(2)和式(3)可得：

$ x \boldsymbol{P}_n^n(x)=y \boldsymbol{P}_n^{n-1}(x), x \boldsymbol{P}_{n-1}^{n-1}(x)=y \boldsymbol{P}_{n-1}^{n-2}(x) $

(17)

在式(9)中，如果取m=(n－1)，则等号右端第3项不存在，将其设置为0，则有：

$ \begin{gathered} (2 n) \boldsymbol{P}_n^{n-1}(x)= \\ (2 n-2)(2 n-1) y \boldsymbol{P}_{n-1}^{n-2}(x)+2(2 n-1) x \boldsymbol{P}_{n-1}^{n-1}(x) \\ =(2 n-2)(2 n-1) x \boldsymbol{P}_{n-1}^{n-1}(x)+ \\ 2(2 n-1) x \boldsymbol{P}_{n-1}^{n-1}(x)=2 n(2 n-1) x \boldsymbol{P}_{n-1}^{n-1}(x) \end{gathered} $

(18)

上式与式(2)完全一致。式(9)取m=n时，等号右端第2项和第3项均不存在，将其设置为0后可直接得到式(3)。式(9)中次的适用范围为1≤m≤n。

式(10)取m=n时，等号右端第2项不存在，将其设置为0，可直接得到式(3)。在式(10)中次的适用范围为1≤m≤n。

式(13)取m=(n－1)时，等号右端第2项不存在，将其设置为0，可直接得到式(2)。式(13)中次的适用范围为0≤m≤(n－1)。

式(15)取m=(n－1)时，等号右端第2项不存在，将其设置为0，则有：

$ \begin{gathered} (2 n-2) \boldsymbol{P}_n^{n-1}(x)=(2 n-1)(2 n-2) y \boldsymbol{P}_{n-1}^{n-2}(x)= \\ (2 n-1)(2 n-2) x \boldsymbol{P}_{n-1}^{n-1}(x) \end{gathered} $

(19)

上式与式(2)完全一致。当式(16)中的m=n时，等号右端第2项不存在，将其设置为0，可直接得到式(3)。式(16)中次的适用范围为1≤m≤n。

3 完整类型的列式递推公式

式(9)、式(10)、式(13)和式(16)都符合列式递推公式的规定，但都不完整，只依靠其中一个递推公式不能完成所有缔合勒让德函数的计算，必须把上述公式适当地组合起来，才能形成一个完整类型的列式递推公式。

3.1 第1种类型的列式递推公式

当m≠0时，采用式(9)；当m=0时，采用式(13)。则有：

$ \begin{gathered} \boldsymbol{P}_n^m(x)= \\ \left\{\begin{array}{l} A_1 x \boldsymbol{P}_{n-1}^0(x)-A_2 y \boldsymbol{P}_{n-1}^1(x), m=0 \\ A_3 y \boldsymbol{P}_{n-1}^{m-1}(x)+A_4 x \boldsymbol{P}_{n-1}^m(x)- \\ \;\;\;A_5 y \boldsymbol{P}_{n-1}^{m+1}(x), m \neq 0 \end{array}\right. \end{gathered} $

(20)

式中，$A_1=1, A_2=\frac{1}{n}, A_3=\frac{(n+m-1)(n+m)}{2 n}, $$A_4=\frac{n+m}{n}, A_5=\frac{1}{2 n} $。基于式(20)，可由0和1阶的缔合勒让德函数数值逐步递推计算出高阶次数值。

3.2 第2种类型的列式递推公式

当m≠0时，采用式(10)；当m=0时，采用式(13)。则有：

$ \begin{gathered} \boldsymbol{P}_n^m(x)= \\ \left\{\begin{array}{l} A_1 x \boldsymbol{P}_{n-1}^0(x)-A_2 y \boldsymbol{P}_{n-1}^1(x), m=0 \\ B_1 y \boldsymbol{P}_{n-1}^{m-1}(x)+B_2 x \boldsymbol{P}_{n-1}^m(x), m \neq 0 \end{array}\right. \end{gathered} $

(21)

式中，$ B_1=(n+m-1), B_2=1$。

基于式(21)，可由0和1阶的缔合勒让德函数数值逐步递推计算出高阶次数值。

3.3 第3种类型的列式递推公式

当m≠n时，采用式(13)；当m=n时，采用式(3)。则有：

$ \begin{gathered} \boldsymbol{P}_n^m(x)= \\ \left\{\begin{array}{l} C_1 x \boldsymbol{P}_{n-1}^m(x)-C_2 y \boldsymbol{P}_{n-1}^{m+1}(x), m \neq n \\ C_3 y \boldsymbol{P}_{n-1}^{n-1}(x), m=n \end{array}\right. \end{gathered} $

(22)

式中，$ C_1=\frac{n+m}{n-m}, C_2=\frac{1}{n-m}, C_3=2 n-1$。

基于式(22)，可由0和1阶的缔合勒让德函数数值逐步递推计算出高阶次数值。

3.4 第4种类型的列式递推公式

当m≠0时，采用式(16)；当m=0时，采用式(13)。则有：

$ \begin{gathered} \boldsymbol{P}_n^m(x)= \\ \left\{\begin{array}{l} A_1 x \boldsymbol{P}_{n-1}^0(x)-A_2 y \boldsymbol{P}_{n-1}^1(x), m=0 \\ D_1 y \boldsymbol{P}_{n-1}^{m-1}(x)+D_2 y \boldsymbol{P}_{n-1}^{m+1}(x), m \neq 0 \end{array}\right. \end{gathered} $

(23)

式中，$ D_1=\frac{(n+m)(n+m-1)}{2 m}, D_2=\frac{1}{2 m}$。

基于式(23)，理论上也可由0和1阶的缔合勒让德函数数值逐步递推计算出高阶次数值。

4 第1种类型列式递推公式的适用性

完全规格化的缔合勒让德函数fnALFs为^[5-6]：

$ \left\{\begin{array}{l} \overline{\boldsymbol{P}}_n^m(x)=\overline{\boldsymbol{N}}_n^m \boldsymbol{P}_n^m(x) \\ \overline{\boldsymbol{N}}_n^m=\sqrt{\frac{\left(2-\delta_0^m\right)(2 n+1)(n-m) !}{(n+m) !}} \end{array}\right. $

(24)

文献[18]给出一种特殊规格化的缔合勒让德函数：

$ \left\{\begin{array}{l} \widetilde{\boldsymbol{P}}_n^m(x)=\widetilde{\boldsymbol{N}}_n^m \boldsymbol{P}_n^m(x) \\ \widetilde{\boldsymbol{N}}_n^m=\frac{2^m n !}{(n+m) !} \end{array}\right. $

(25)

根据缔合勒让德函数定义及式(24)和式(25)，可求得不同规格化情况下0和1阶的缔合勒让德函数为：$ \boldsymbol{P}_0^0(x)=\widetilde{\boldsymbol{P}}_0^0(x)=1, \boldsymbol{P}_1^0(x)=\widetilde{\boldsymbol{P}}_1^0(x)=x, $$\boldsymbol{P}_1^1(x)=\widetilde{\boldsymbol{P}}_1^1(x)=y, \overline{\boldsymbol{P}}_0^0(x)=1, $$\overline{\boldsymbol{P}}_1^0(x)=\sqrt{3} x, \overline{\boldsymbol{P}}_1^1(x)=\sqrt{3} y $

fnALFs第n阶整体数值精度的检验公式如下^[12]：

$ \begin{gathered} T(n)=\frac{1}{(2 n+1)} \cdot \\ \left|(2 n+1)-\sum\limits_{m=0}^n\left[\overline{\boldsymbol{P}}_n^m(x)\right]^2\right|<\mathrm{EPS} \end{gathered} $

(26)

式中，EPS为相对误差，在地球重力场计算中一般要求EPS < 10^-9。若第n阶所有fnALFs数值均满足式(26)，则说明其数值计算精度满足要求。

4.1 间接计算方法

利用式(25)对式(20)进行特殊规格化处理：

$ \begin{gathered} \widetilde{\boldsymbol{P}}_n^m(x)= \\ \left\{\begin{array}{l} \widetilde{A}_1 x \widetilde{\boldsymbol{P}}_{n-1}^0(x)-\widetilde{A}_2 y \widetilde{\boldsymbol{P}}_{n-1}^1(x), \\ \;\;\;\;\;m=0 \\ \widetilde{A}_3 y \widetilde{\boldsymbol{P}}_{n-1}^{m-1}(x)+\widetilde{A}_4 x \widetilde{\boldsymbol{P}}_{n-1}^m(x)- \\ \;\;\;\;\;{\widetilde{A}_5} y \widetilde{\boldsymbol{P}}_{n-1}^{m+1}(x), m \neq 0 \end{array}\right. \end{gathered} $

(27)

式中，$ \widetilde{A}_1=\widetilde{A}_3=\widetilde{A}_4=1, \widetilde{A}_2=0.5, \widetilde{A}_5=0.25$。

根据式(24)和式(25)可知，$\widetilde{\boldsymbol{P}}_n^m(x) \text { 与 } \overline{\boldsymbol{P}}_n^m(x) $的转换关系为：

$ \begin{aligned} & \overline{\boldsymbol{P}}_n^m(x)=\sqrt{(2 n+1)} K_n^m \widetilde{\boldsymbol{P}}_n^m(x) \\ & K_n^m=\sqrt{\left(2-\delta_0^m\right) \frac{(n+m) !}{2^m n !} \frac{(n-m) !}{2^m n !}} \end{aligned} $

(28)

式中，K_n⁰=K₁¹=1。通常采用以下递推公式计算K_n^m：

$ K_n^m=\left\{\begin{array}{l} D_1 K_{n-1}^m, m \neq n \\ D_2 K_{n-1}^{n-1}, m=n \end{array}\right. $

(29)

式中，$ D_1=\sqrt{1-\left(\frac{m}{n}\right)^2}, D_2=\sqrt{\frac{2 n-1}{2 n}}$。

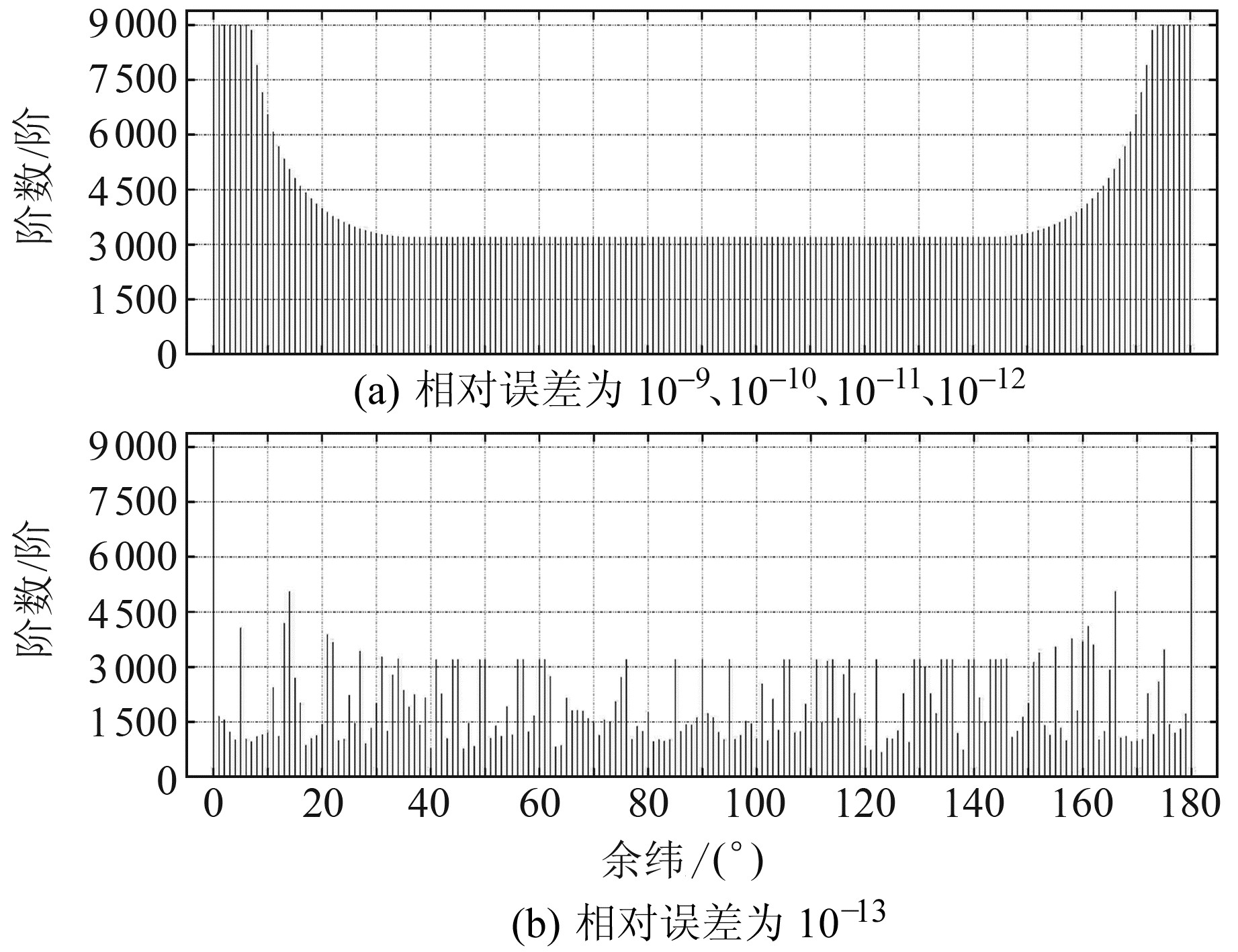
根据精度检验公式(26)，可得式(27)的适用性(图 1)。由图可见，当相对误差EPS=10^-9、10^-10、10^-11和10^-12时，式(27)的适用性和普适性完全一致，在任何纬度处都可递推计算至3 193阶，即普适性为3 193阶；两极附近可至少递推至9 000阶(设置的最大二维数组)，即两极处的适用性为9 000阶。当EPS=10^-13时，递推公式(27)的普适性仅为664阶，且不同纬度处的适用性不稳定。

4.2 直接计算方法

对式(20)进行完全规格化处理：

$ \begin{gathered} \overline{\boldsymbol{P}}_n^m(x)= \\ \left\{\begin{array}{l} \bar{A}_1 x \overline{\boldsymbol{P}}_{n-1}^0(x)-\bar{A}_2 y \overline{\boldsymbol{P}}_{n-1}^1(x), m=0 \\ \bar{A}_3 y \overline{\boldsymbol{P}}_{n-1}^{m-1}(x)+\bar{A}_4 x \overline{\boldsymbol{P}}_{n-1}^m(x)- \\ \bar{A}_5 y \overline{\boldsymbol{P}}_{n-1}^{m+1}(x), m \geqslant 1 \end{array}\right. \end{gathered} $

(30)

式中，$ \bar{A}_1=\sqrt{\frac{(2 n+1)}{(2 n-1)}}, \bar{A}_2=\sqrt{\frac{(2 n+1)(n-1)}{(2 n)(2 n-1)}}, $$\bar{A}_3=\frac{1}{2 n} \sqrt{\frac{2(2 n+1)(n+m-1)(n+m)}{\left(2-\delta_0^{m-1}\right)(2 n-1)}}, $$\bar{A}_4=\frac{1}{n} \sqrt{\frac{(2 n+1)(n+m)(n-m)}{(2 n-1)}}, $$\bar{A}_5=\frac{1}{2 n} \sqrt{\frac{(2 n+1)(n-m-1)(n-m)}{(2 n-1)}} $。

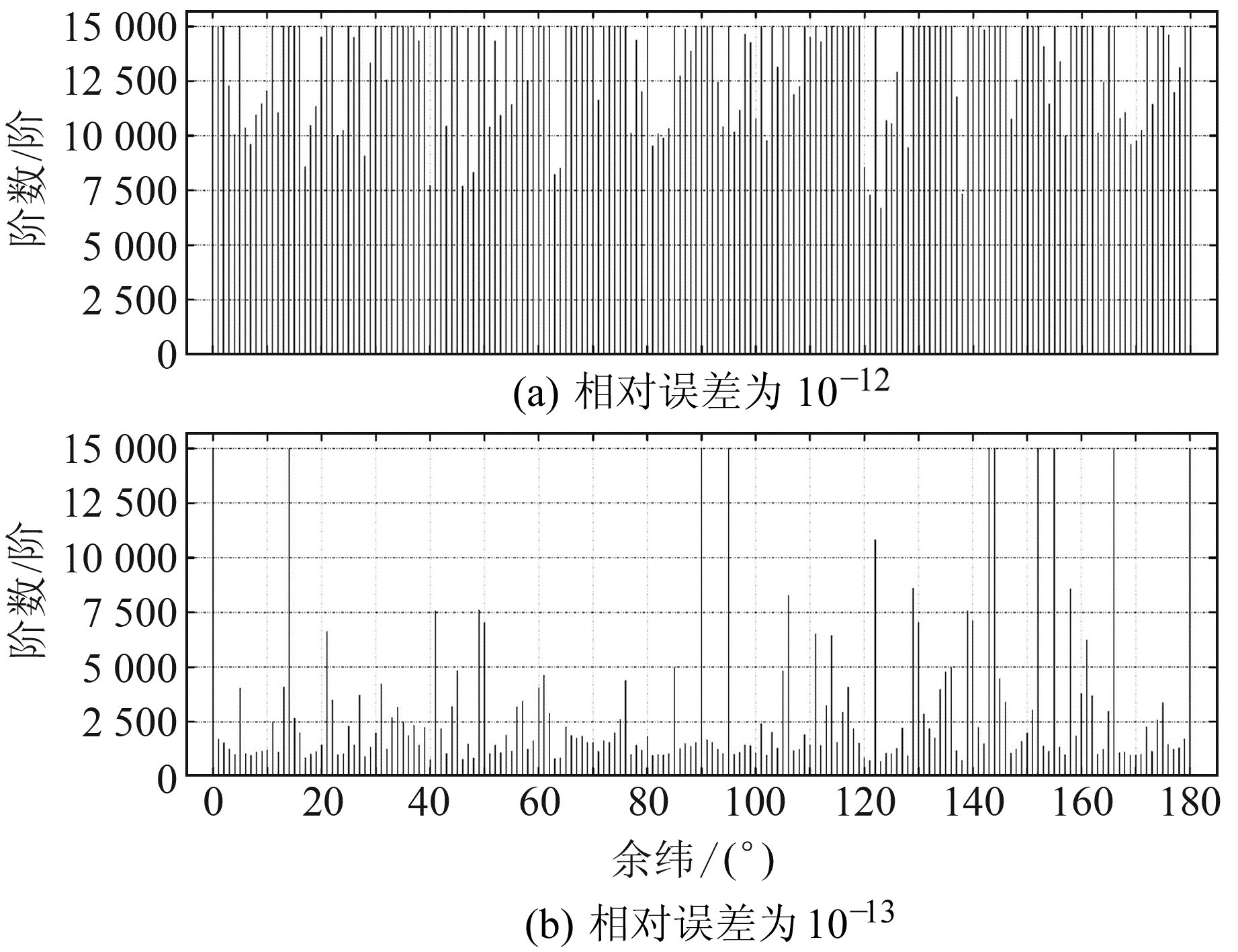
根据式(26)选择EPS=10^-11时，式(30)的普适性至少有15 000阶(设置的二维数组上限)。即在任意纬度处，利用式(30)可将fnALFs数值至少递推至15 000阶。选择EPS=10^－12、10^－13时，其适用性和普适性如图 2所示。

由图 2可见，当EPS=10^-12时，式(30)的普适性为6 684阶；当EPS=10^-13时，普适性仅为668阶，且不同纬度处的适用性不稳定。实际上，式(27)和(30)完全等价，式(27)采用特殊规格化间接算法，递推至3 100阶时会出现溢出现象；式(30)是完全规格化的直接算法，可至少直接递推至15 000阶。由此可见，即使是同一个公式，不同的计算过程会得出完全不同的结果。

5 其他类型列式递推公式的适用性 5.1 第2种类型的适用性

对式(21)进行完全规格化处理：

$ \begin{gathered} \overline{\boldsymbol{P}}_n^m(x)= \\ \left\{\begin{array}{l} \bar{A}_1 x \overline{\boldsymbol{P}}_{n-1}^0(x)-\bar{A}_2 y \overline{\boldsymbol{P}}_{n-1}^1(x), m=0 \\ \bar{B}_1 y \overline{\boldsymbol{P}}_{n-1}^{m-1}(x)+\bar{B}_2 x \overline{\boldsymbol{P}}_{n-1}^m(x), m \neq 0 \end{array}\right. \end{gathered} $

(31)

式中，$ \bar{B}_1=\sqrt{\frac{2(2 n+1)(n+m-1)}{\left(2-\delta_0^{m-1}\right)(2 n-1)(n+m)}}$，$\bar{B}_2=\sqrt{\frac{(2 n+1)(n-m)}{(2 n-1)(n+m)}} $。

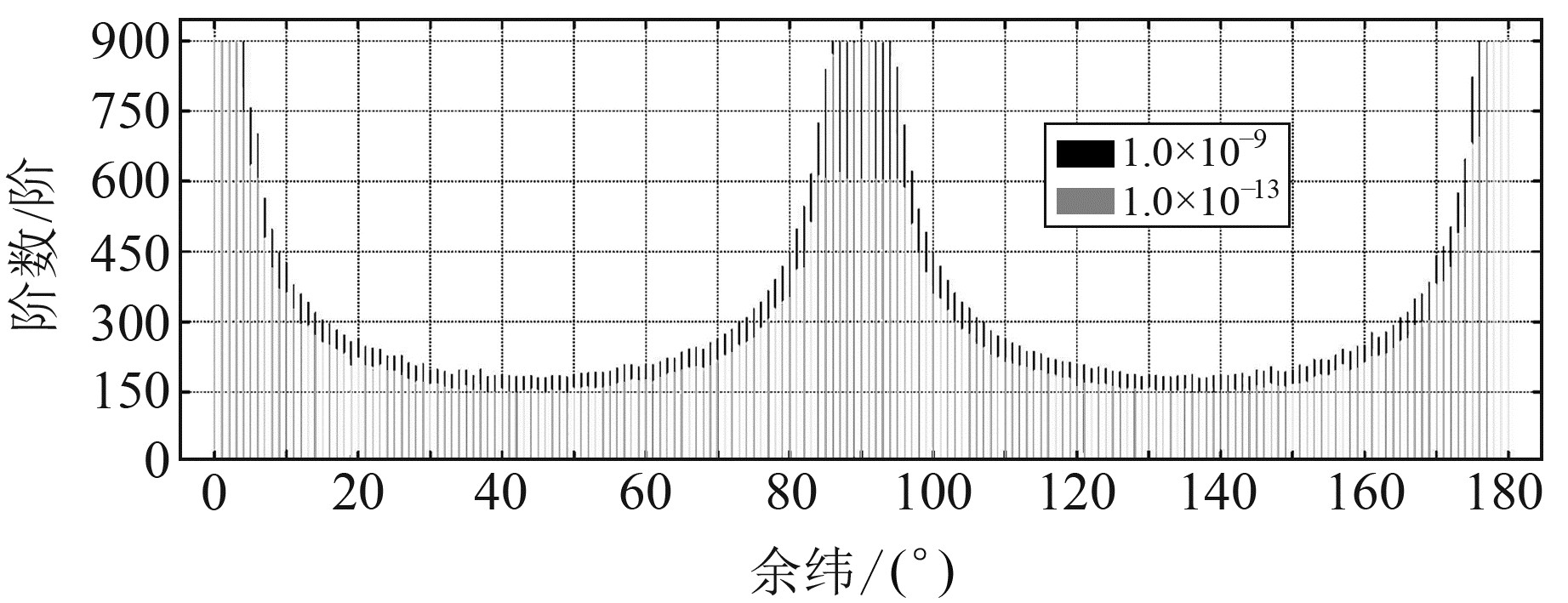
根据式(26)得到式(31)的适用性和普适性如图 3所示。

由图 3可见，式(31)的普适性仅为150阶。仅在赤道和两极点附近区域有较好的适用性，在南北中纬度区域的适用性较差。

5.2 第3种和第4种类型的列式递推公式

对式(22)进行完全规格化处理：

$ \begin{gathered} \overline{\boldsymbol{P}}_n^m(x)= \\ \left\{\begin{array}{l} \bar{C}_1 x \overline{\boldsymbol{P}}_{n-1}^m(x)-\bar{C}_2 y \overline{\boldsymbol{P}}_{n-1}^{m+1}(x), m \neq n \\ \bar{C}_3 y \overline{\boldsymbol{P}}_{n-1}^{n-1}(x), m=n \end{array}\right. \end{gathered} $

(32)

式中，$ \bar{C}_1=\sqrt{\frac{(2 n+1)(n+m)}{(2 n-1)(n-m)}}$，$\bar{C}_2=\sqrt{\frac{\left(2-\delta_0^m\right)(2 n+1)(n-m-1)}{2(2 n-1)(n-m)}} $，$\bar{C}_3=\sqrt{\frac{(2 n+1)}{2 n}} $。

计算结果表明，式(32)和式(31)的适用性基本一致。

对式(23)进行完全规格化处理：

$ \begin{gathered} \overline{\boldsymbol{P}}_n^m(x)= \\ \left\{\begin{array}{l} \bar{A}_1 x \overline{\boldsymbol{P}}_{n-1}^0(x)-\bar{A}_2 y \overline{\boldsymbol{P}}_{n-1}^1(x), m=0 \\ \bar{D}_1 y \overline{\boldsymbol{P}}_{n-1}^{m-1}(x)+\bar{D}_2 y \overline{\boldsymbol{P}}_{n-1}^{m+1}(x), m \neq 0 \end{array}\right. \end{gathered} $

(33)

式中，$ \bar{D}_1=\frac{1}{2 m} \sqrt{\frac{2(2 n+1)(n+m)(n+m-1)}{\left(2-\delta_0^{m-1}\right)(2 n-1)}}$，$\bar{D}_2=\frac{1}{2 m} \sqrt{\frac{(2 n+1)(n-m-1)(n-m)}{(2 n-1)}} $。

计算结果表明，式(33)和式(31)的适用性也基本一致。

式(31)、(32)和(33)均可称为列式递推公式，与式(30)相比更加简单，但适用性和普适性较差。实际上，递推公式的优劣取决于递推系数，递推系数越小，递推公式的适用性和普适性就越好。例如，式(30)中的系数$\bar{A}_j(j=1, 2, \cdots, 5) \text { 在 } n \geqslant 2 $时均满足要求，因此利用式(30)可计算得到较高阶次的fnALFs；当m=1时，式(31)中的系数$\bar{B}_1>1 $，因此递推公式(31)的普适性仅为150阶，适用性也较差；当m=(n－1)时，$\bar{C}_1=\sqrt{2 n+1} $；当m=1时，$\bar{D}_1=\frac{1}{2} \sqrt{\frac{2(2 n+1)(n+1)(n)}{(2 n-1)}} $。因此，递推公式(32)和(33)只有理论意义，无实际计算价值。

6 结语

结果表明，当EPS=10^-11时，直接算法的普适性至少有15 000阶；当EPS=10^-12时，普适性约为6 600阶。与标准向前按列/次递推公式相比，递推公式的优势是在所有纬度处的普适性都较好，不足之处是适用性不稳定。

本文给出Belikov^[18]递推公式的证明，同时提出新的列式递推公式，但新的列式递推公式都不适用于高阶次的递推计算，仅在理论上作为列式递推公式的补充。