2. 中国地震局地震研究所,武汉市洪山侧路40号,430071;
3. 中国地震局地震大地测量重点实验室,武汉市洪山侧路40号,430071;
4. 湖北省地震局,武汉洪山侧路48号,430071
受扫描范围、物体遮挡等限制,激光扫描仪难以通过单次扫描获得完整模型,而是需要将不同视角的点云数据统一到同一坐标系中。通常在2台仪器的公共扫描范围内放置至少3个标靶球,先定位其球心坐标,再通过刚体变换实现配准。然而粗差会使球心定位出现明显偏差,因此在含有异常值的点云数据中,准确估计球心坐标是点云配准的关键[1]。
在点云数据只含有随机误差的情况下进行标靶球定位时,一般采用最小二乘法(LS)计算其几何中心[2]。然而系数矩阵中也含有存在误差的观测值,需要使用总体最小二乘法(TLS)建立EIV模型对球心进行定位。鲁铁定等[3]使用奇异值分解方法得到TLS估计值;陈玮娴等[4]基于点云入射角对坐标进行定权;陶武勇等[5]使用双非线性TLS法进行2次线性化处理获得参数解。但上述TLS法均需要进行迭代求解,每次迭代均存在大量的矩阵运算,算法复杂度较高。
由于点云数据中难免含有粗差,因此需要将稳健估计理论应用到标靶球定位中。Zhou等[6]提出基于M估计的稳健球心估计方法,能够确定含有粗差的点云数据中心坐标;王乐洋等[7]提出适用于球心定位的稳健总体最小二乘法(RTLS),在迭代过程中,需根据3倍中误差准则剔除粗差。然而,M估计和RTLS估计均依赖于迭代初值,容易收敛至错误的估计值,崩溃率有限,且TLS法需要迭代求解,半径估计值有偏。
针对上述问题,潘国荣等[8]使用基于忠实距离的代数拟合方法,采用Pratt方法[9]求解参数。结果表明,该方法基本等效于几何拟合法,且在计算上更具优势。在此基础上,本文进一步顾及算法的稳健性,融合加权Hyper方法[10]和截断最小二乘法(LTS)实现快速稳健的球心定位。与2种常用的稳健球心定位算法相比,本文算法的崩溃率和计算效率都有显著提高。
1 加权Hyper方法加权Hyper方法具有以下优点:1)具有与几何拟合相同的估计精度;2)参数估计值满足无偏性;3)计算简单,仅需计算五阶矩阵的特征值便能定位球心。常见的球面拟合准则分为几何准则和代数准则,几何准则必须进行迭代求解,而代数准则基于球的代数方程,无需迭代。代数准则的目标函数为:
| $ \begin{gathered} \sum\limits_{i=1}^n f^2\left(x_i, y_i, z_i\right)= \\ \sum\limits_{i=1}^n\left[A\left(x_i^2+y_i^2+z_i^2\right)+\right. \\ \left.B x_i+C y_i+D z_i+E\right]^2=\min \end{gathered} $ | (1) |
式中,(xi, yi, zi)为球面离散点观测值;A、B、C、D、E均为待估参数,待估参数与球心c和半径R的转换可表达为:
| $ \boldsymbol{c}=\left[-\frac{B}{2 A}, -\frac{C}{2 A}, -\frac{D}{2 A}\right]^{\mathrm{T}} $ | (2) |
| $ R=\sqrt{B^2+C^2+D^2-4 A E} / 2 A $ | (3) |
文献[8]中的最小化忠实距离平方和为
| $ \sum\limits_{i=1}^n \frac{p_i f^2\left(x_i, y_i, z_i\right)}{4 R^2}=\min $ | (4) |
式中,pi为点i的权值,本文借鉴入射角定权方法[4],设置pi=cosθi。
令
| $ \boldsymbol{u}^{\mathrm{T}}\left(\boldsymbol{X}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{X}\right) \boldsymbol{u}=\min \quad \text { s. t. } \boldsymbol{u}^{\mathrm{T}} \boldsymbol{N}_P \boldsymbol{u}=1 $ | (5) |
| $ \boldsymbol{u}^{\mathrm{T}}\left(\boldsymbol{X}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{X}\right) \boldsymbol{u}=\min \quad \text { s. t. } \boldsymbol{u}^{\mathrm{T}} \boldsymbol{N}_T \boldsymbol{u}=1 $ | (6) |
式中,
| $ \boldsymbol{u}^{\mathrm{T}}\left(\boldsymbol{X}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{X}\right) \boldsymbol{u}=\min \quad \text { s. t. } \boldsymbol{u}^{\mathrm{T}}\left(\boldsymbol{N}_P-2 \boldsymbol{N}_T\right) \boldsymbol{u}=1 $ | (7) |
使用奇异值分解法分解矩阵
尽管加权Hyper方法具备很多优点,但是容易因粗差而崩溃。为消除粗差影响,根据LTS的估计准则引入截断参数h,抽样得到子集并检验其目标函数。LTS方法的线性回归函数模型可表示为:
| $ \boldsymbol{y}=\boldsymbol{A x}+\boldsymbol{e} $ | (8) |
式中,y、A分别为观测向量和系数矩阵,x为待估参数向量,e为独立等精度的误差向量。LS为最佳线性无偏估计,对粗差极其敏感,其准则为
| $ \sum\limits_{i=1}^h e_i^2=\min \left(e_1^2<e_2^2<\cdots<e_n^2\right) $ | (9) |
LTS方法通过抽样检验求解参数,在数据被污染一半的情况下仍能抵抗粗差的干扰,具有渐近正态性和高崩溃率。
3 快速稳健的标靶球定位方法本文结合Hyper方法和LTS方法提出一种新的快速稳健的标靶球定位方法。根据粗差比例κ设置子集中观测值的数量为
| $ l=\frac{\log (1-p)}{\log \left(1-(1-\kappa)^m\right)} $ | (10) |
式中,p为选到不受粗差污染的子集概率,实验中设置p=99%。重复以下3个步骤l次,选择目标函数最小时的估计值作为输出值:
1) 随机选择不在一个平面上的m=4个点,固定参数A=1,利用球面上的4点直接确定球面参数u。进一步计算点i(i=1, 2, …, n)的加权忠实距离平方ri2:
| $ r_i^2=\frac{p_i f^2\left(x_i, y_i, z_i\right)}{4 R^2} $ | (11) |
2) 将所有数据点的ri2进行升序排列(
3) 使用加权Hyper方法计算步骤2)中的子集,得到u的估计值。将加权忠实距离平方按照升序排列,将前h个最小的加权忠实距离平方和作为目标函数。
步骤1)是为了减少抽样次数。根据式(10)可知,若直接设置抽样数量m=h,则抽样次数l会迅速增加;步骤2)的主要目的是保证步骤3)中有更多的正常观测值参与平差计算,增强有效性;步骤3)中的加权Hyper方法不同于几何拟合算法,无需迭代即可定位球心。该方法的目标函数为
| $ \hat{\sigma}=\sqrt{\sum\limits_{i=1}^h r_i^2 /(h-m)} $ | (12) |
使用RIEGL VZ-1000激光扫描仪扫描R=7.25 cm的标靶球,获得835个点云数据,经重心化处理后的球心为
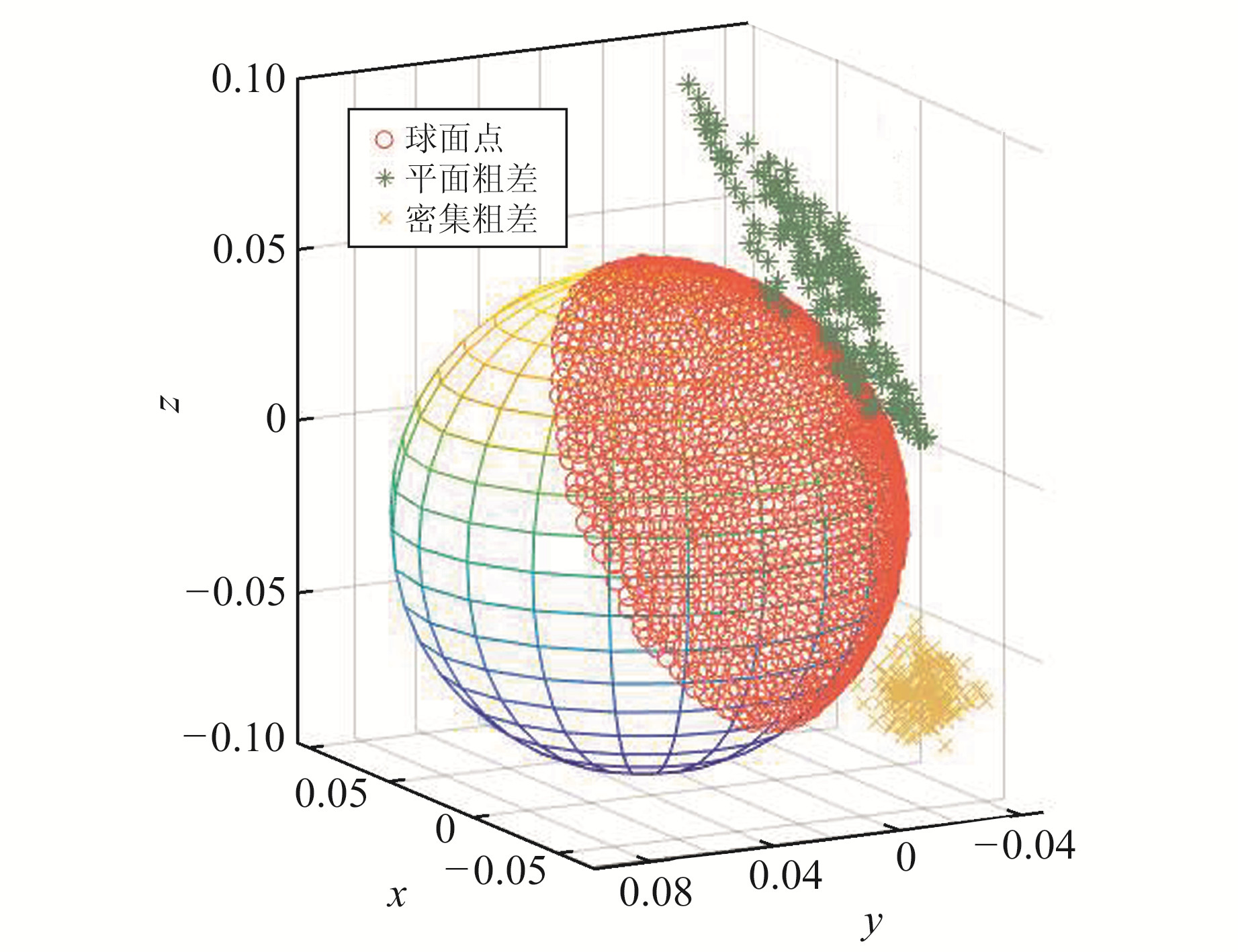
|
图 1 点云分布 Fig. 1 The distribution of point cloud |
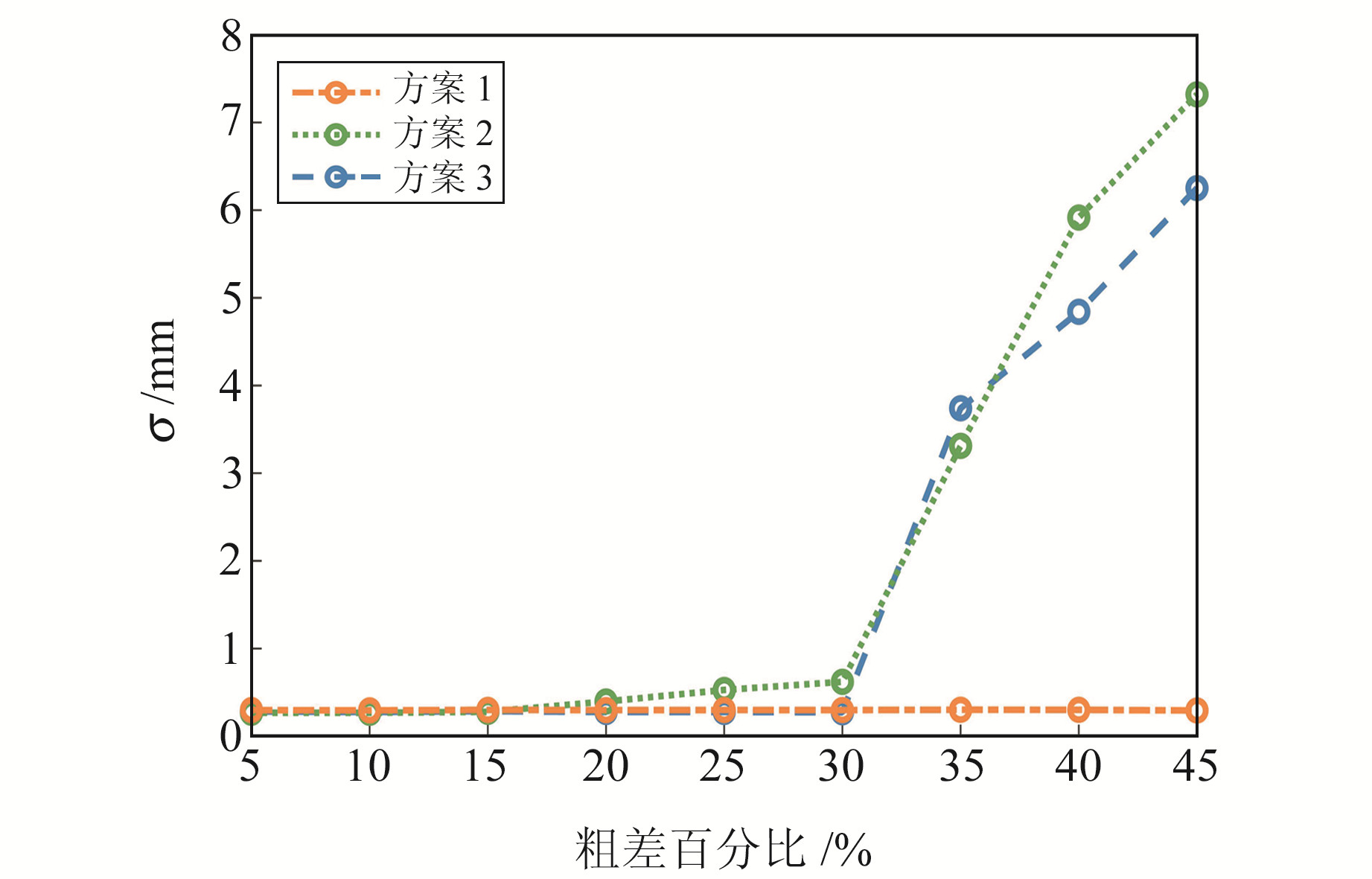
|
图 2 单位权中误差估计值 Fig. 2 The estimation of standard error of unit weight |
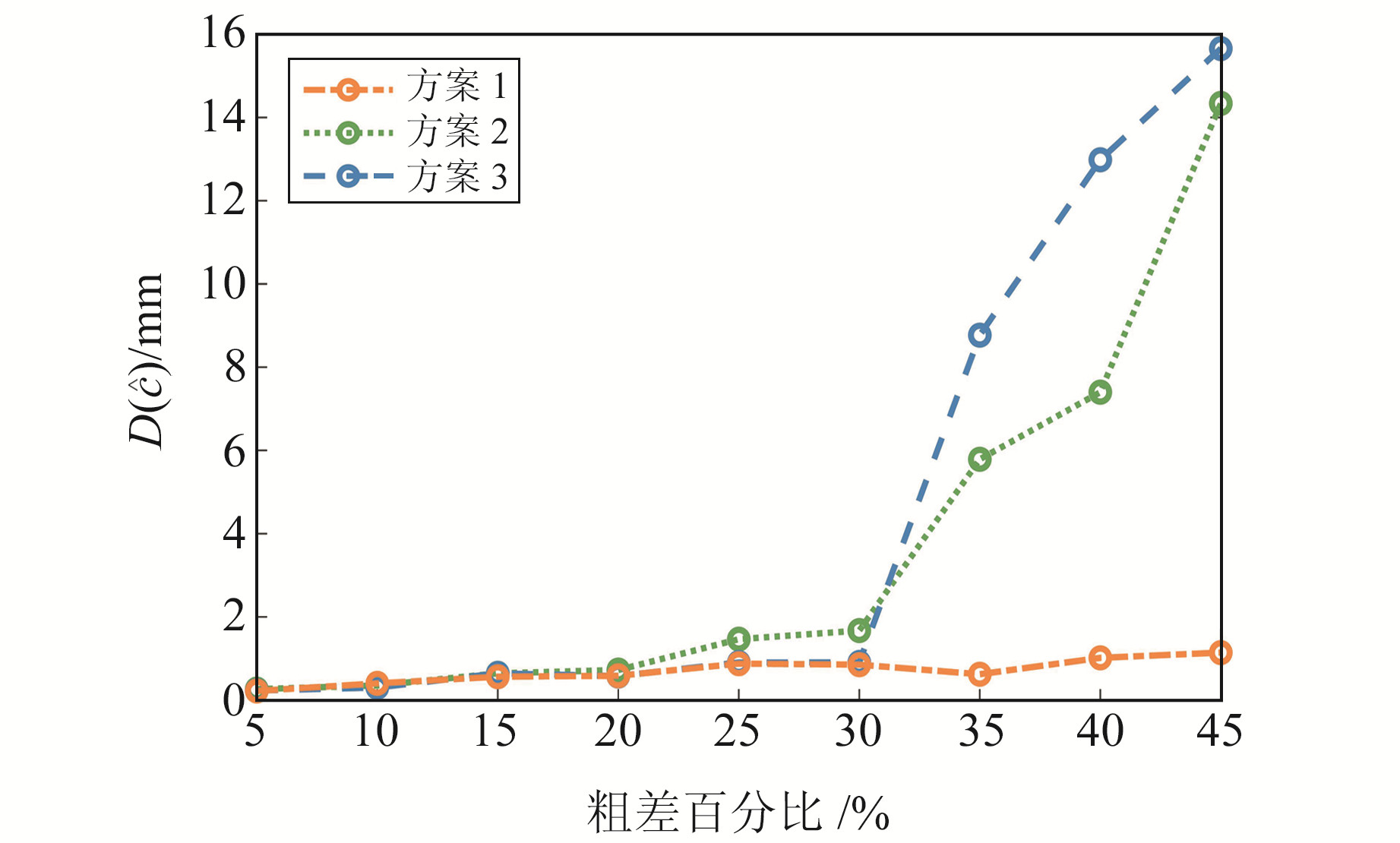
|
图 3 平均球心偏差 Fig. 3 The average deviation of ball center |
由图 2、3可见,当污染率小于20%时,各方案均能较为准确地定位球心,表明3种算法都具有一定的稳健性。其中方案1和方案2的差异并不显著,说明本文基于忠实距离准则的算法等效于基于几何距离准则的TLS方法;当污染率增加到25%~30%时,方案2的2个指标大于其他2种方案;当污染率大于30%时,方案3的2个指标也明显增大,说明粗差探测法和M估计法的崩溃率有限。本文算法的2个指标波动较小,实验中算法崩溃率高达45%。
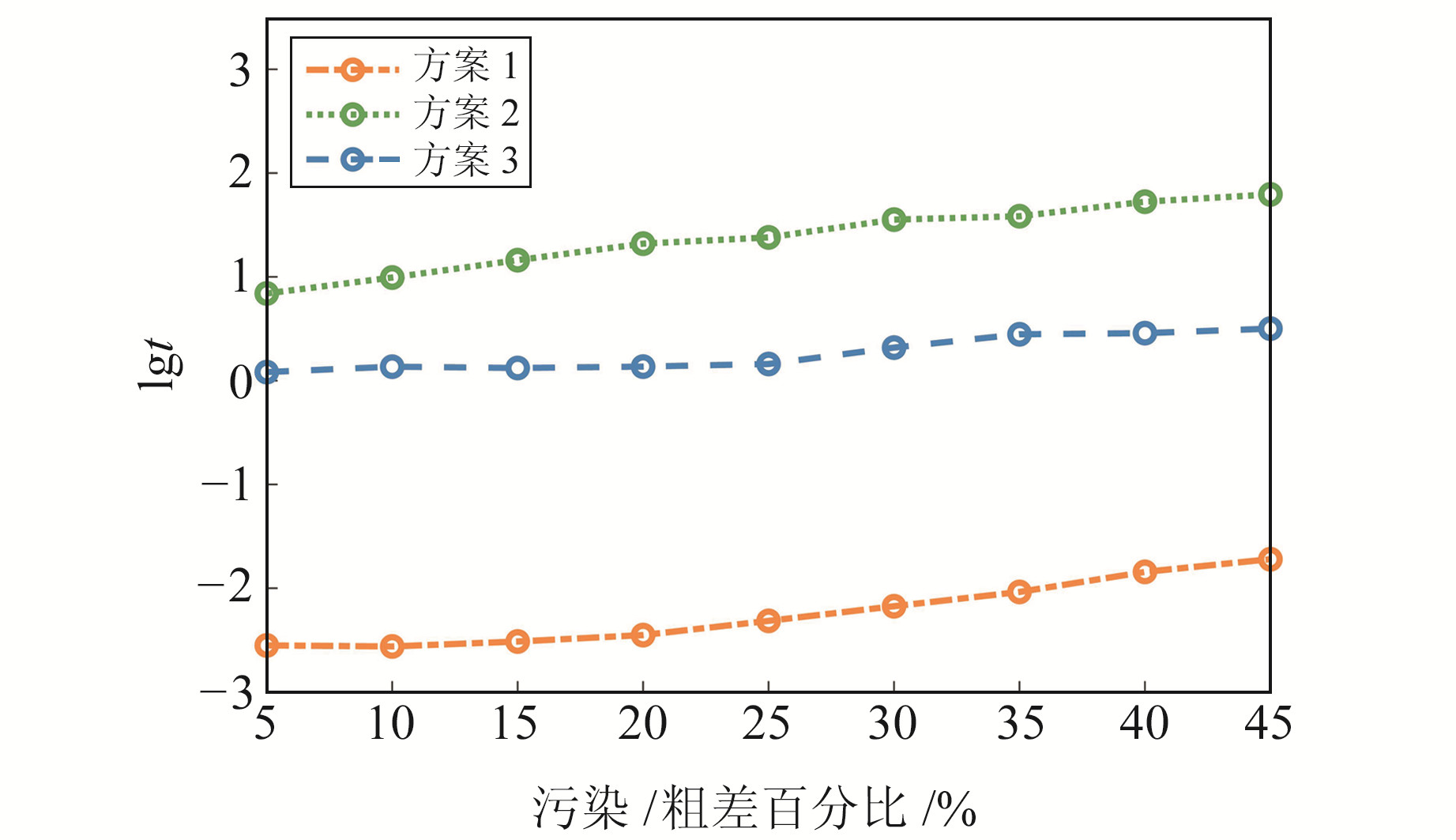
进一步比较3种算法的计算效率,图 4和图 5分别为3个方案的运行次数和平均运行时间t的对数lgt。由图 4可见,方案2和方案3的迭代次数较多,而方案1属于抽样检验算法,无需设置初值,运行次数最少。由图 5可见,3种算法的运行时间量级分别为10-2 s、101 s和100 s,本文算法运行时间远小于其他2种方案。这是因为在迭代过程中,RTLS需要进行复杂的大型矩阵乘法和求逆运算,点云数量较多,耗时较长;M估计法在迭代过程中需要重新线性化和定权,增加了参数解算时间;本文算法通过Hyper方法直接得到估计值,过程中仅进行五阶矩阵的运算,运算量显著减少,因此运行时间的量级明显低于其他2种算法。
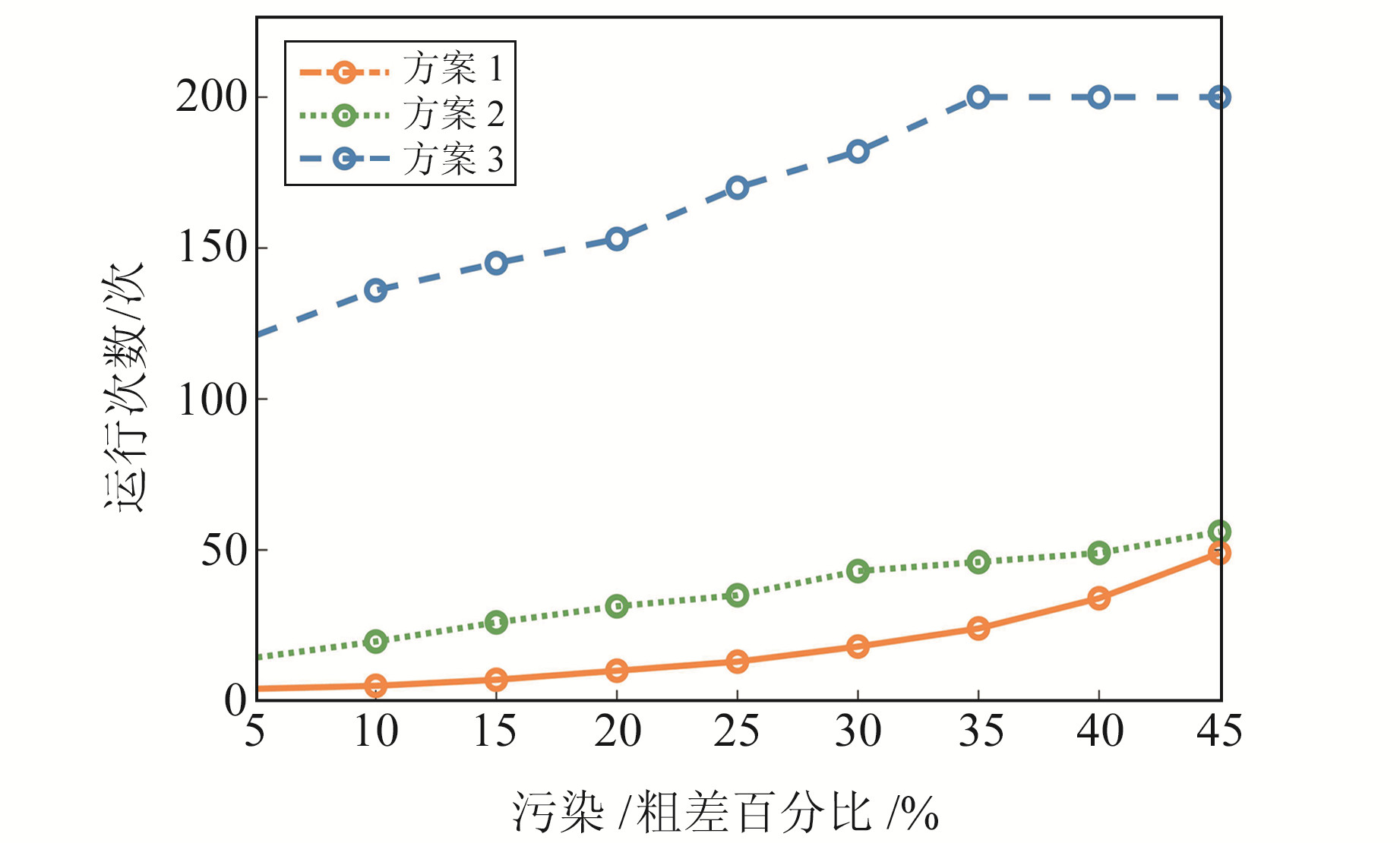
|
图 4 3种方案的运行次数 Fig. 4 The running times of the three methods |
|
图 5 3种方案的lgt Fig. 5 lgt of the three methods |
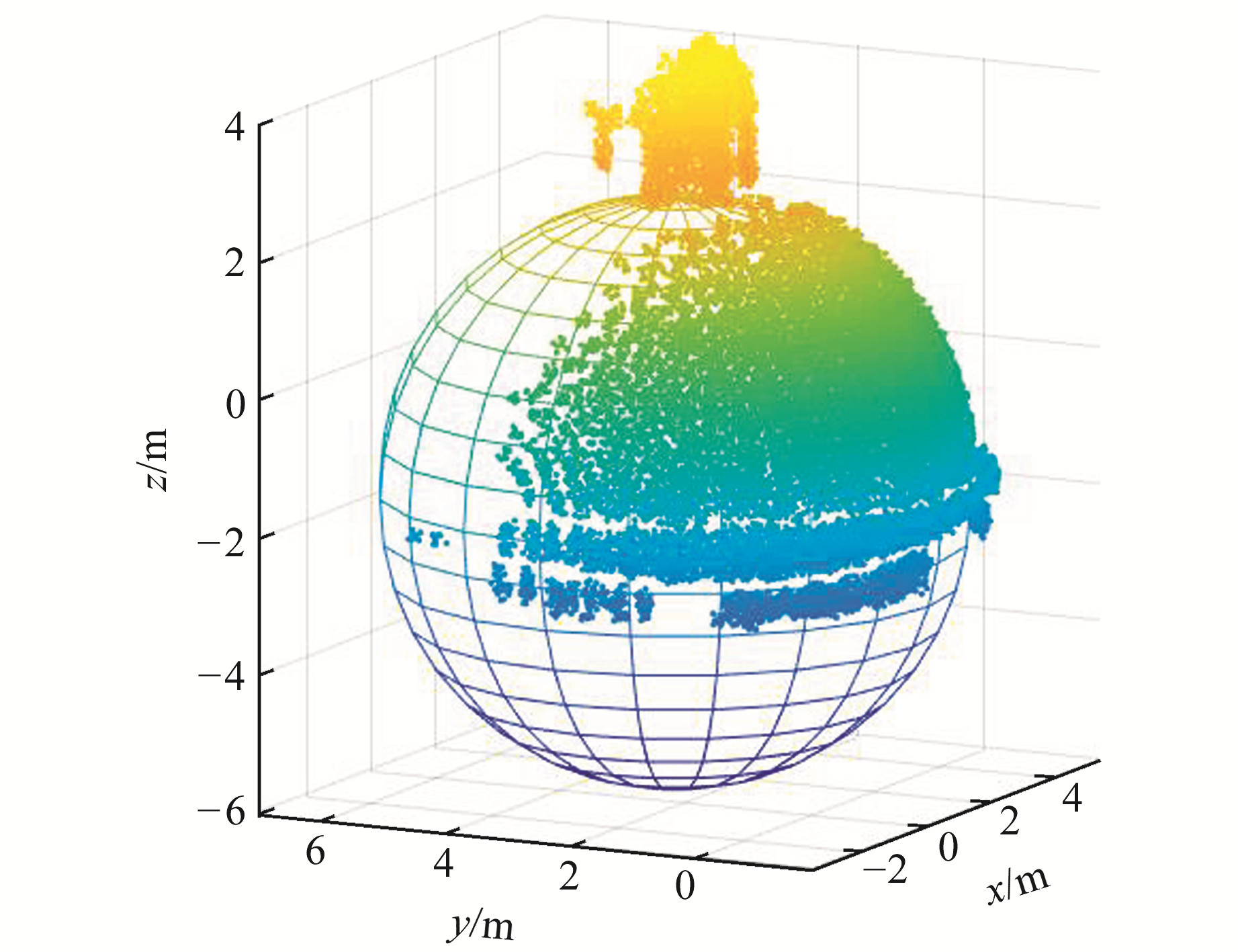
选择WHU-TLS数据集[14]中校园场景的球形建筑数据测试本文算法的性能。该数据有23 440个点,点云分布和球面拟合结果如图 6所示,其中下方环状点云和上方聚集点云在球心定位中属于粗差。从拟合效果上可以看出,本文算法能够有效区分粗差和正常观测值,具有较强的稳健性。实验抽样次数为19,总共耗时0.14 s,说明本文算法具有极高的运算效率,且效率并没有随点云数量的增加而快速下降。
|
图 6 拟合结果 Fig. 6 The fitted results |
本文结合LTS方法和加权Hyper方法提出一种快速稳健的球心定位算法。该算法减少了传统算法复杂矩阵的迭代计算,能够有效抵御粗差干扰。与2种传统算法相比,本文算法的崩溃率更高且解算时间更短,适合处理带有粗差的标靶球点云数据。
| [1] |
Lai J Y, Ueng W D, Yao C Y. Registration and Data Merging for Multiple Sets of Scan Data[J]. The International Journal of Advanced Manufacturing Technology, 1999, 15(1): 54-63 DOI:10.1007/s001700050039
(  0) 0) |
| [2] |
Shakarji C M. Least-Squares Fitting Algorithms of the NIST Algorithm Testing System[J]. Journal of Research of the National Institute of Standards and Technology, 1998, 103(6): 633-641 DOI:10.6028/jres.103.043
(  0) 0) |
| [3] |
鲁铁定, 周世健, 张立亭, 等. 基于整体最小二乘的地面激光扫描标靶球定位方法[J]. 大地测量与地球动力学, 2009, 29(4): 102-105 (Lu Tieding, Zhou Shijian, Zhang Liting, et al. Sphere Target Fixing of Point Cloud Data Based on TLS[J]. Journal of Geodesy and Geodynamics, 2009, 29(4): 102-105)
(  0) 0) |
| [4] |
陈玮娴, 陈义, 袁庆, 等. 加权总体最小二乘在三维激光标靶拟合中的应用[J]. 大地测量与地球动力学, 2010, 30(5): 90-96 (Chen Weixian, Chen Yi, Yuan Qing, et al. Application of Weighted Total Least-Squares to Target Fitting of Three-Dimensional Laser Scanning[J]. Journal of Geodesy and Geodynamics, 2010, 30(5): 90-96)
(  0) 0) |
| [5] |
陶武勇, 鲁铁定, 吴飞, 等. 求解球面拟合的改进总体最小二乘算法[J]. 大地测量与地球动力学, 2018, 38(1): 92-96 (Tao Wuyong, Lu Tieding, Wu Fei, et al. An Improved Total Least Squares Algorithm for Solving Sphere Surface Fitting[J]. Journal of Geodesy and Geodynamics, 2018, 38(1): 92-96)
(  0) 0) |
| [6] |
Zhou S J, Guan Y L, Zhan X W, et al. Sphere Target Fitting of Point Cloud Data Based on M-Estimation[C]. 2009 Sixth International Conference on Fuzzy Systems and Knowledge Discovery, Tianjin, 2009
(  0) 0) |
| [7] |
王乐洋, 陈汉清, 林永达, 等. 利用稳健WTLS方法进行三维激光扫描标靶球定位[J]. 大地测量与地球动力学, 2016, 36(8): 745-749 (Wang Leyang, Chen Hanqing, Lin Yongda, et al. Spherical Target Positioning of 3D Laser Scanning by Using Robust WTLS Method[J]. Journal of Geodesy and Geodynamics, 2016, 36(8): 745-749)
(  0) 0) |
| [8] |
潘国荣, 房鹤飞, 唐杭. 基于等效全最小二乘准则的稳健球面拟合方法[J]. 测绘通报, 2013(增1): 99-102 (Pan Guorong, Fang Hefei, Tang Hang. An Robust Sphere Fitting Methods Based on the Equivalent Full Least Squares[J]. Bulletin of Surveying and Mapping, 2013(S1): 99-102)
(  0) 0) |
| [9] |
Pratt V. Direct Least-Squares Fitting of Algebraic Surfaces[J]. ACM Siggraph Computer Graphics, 1987, 21(4): 145-152
(  0) 0) |
| [10] |
Sharadqah A, Chernov N. Error Analysis for Circle Fitting Algorithms[J]. Electronic Journal of Statistics, 2009, 3: 886-911
(  0) 0) |
| [11] |
Taubin G. Estimation of Planar Curves, Surfaces, and Nonplanar Space Curves Defined by Implicit Equations with Applications to Edge and Range Image Segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(11): 1 115-1 138
(  0) 0) |
| [12] |
Chernov N. Circular and Linear Regression: Fitting Circles and Lines by Least Squares[M]. Florida: CRC Press, 2010
(  0) 0) |
| [13] |
Rousseeuw P J. Least Median of Squares Regression[J]. Journal of the American Statistical Association, 1984, 79(388): 871-880
(  0) 0) |
| [14] |
Dong Z, Yang B S, Liang F X, et al. Hierarchical Registration of Unordered TLS Point Clouds Based on Binary Shape Context Descriptor[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2018, 144: 61-79
(  0) 0) |
2. Institute of Seismology, CEA, 40 Hongshance Road, Wuhan 430071, China;
3. Key Laboratory of Earthquake Geodesy, CEA, 40 Hongshance Road, Wuhan 430071, China;
4. Hubei Earthquake Agency, 48 Hongshance Road, Wuhan 430071, China
 2023, Vol. 43
2023, Vol. 43


