土壤湿度作为基本的气候变量,参与并影响着水文、气候、生态系统中的许多重要过程[1]。星载全球导航卫星系统反射测量GNSS-R技术可直接接收经地表反射的导航定位信号,构成被动的双基地前向散射雷达。其接收机具有低重量、低功耗和低成本等优点,可搭载在低轨卫星上组网实现高时空分辨率的对地探测。通过星载GNSS-R验证任务获取的观测数据,并对地表土壤湿度数据进行相关性分析后发现,反射测量标定量可以很好地对地表土壤湿度的动态变化作出响应[2-3]。随后的定量反演研究中,首先假定GNSS信号在地表仅发生相干反射,然后对标定的有效反射率进行栅格化处理,最后匹配其他观测系统获取的参考土壤湿度建立反演模型。结果表明,反演精度与星载辐射计的精度接近[4-6]。涉及到的反演方法可分为经验建模和机器学习2大类,二者的反演精度相当[7-8]。传统经验反演方法包括栅格化后在每个格网像素上独立拟合的经验模型[7, 9]以及在研究区内建立的统一反演模型2大类[5-6]。
由于不同研究中的数据时段、研究区空间范围、使用的辅助参数以及反演的时空分辨率存在差异,目前鲜有学者对不同经验建模的反演效果进行评价。本文使用气旋全球导航卫星系统CYGNSS提供的观测数据和土壤湿度主被动项目SMAP提供的地表土壤湿度及其植被和地表特征参数,在相同的反演时空分辨率下对比评价2种主流经验星载GNSS-R地表土壤湿度反演方法的性能,为后续研究提供参考。
1 数据与方法 1.1 CYGNSS数据CYGNSS是由8颗低轨小卫星组成的卫星星座,观测范围覆盖南北纬38°区域,其搭载的时延多普勒接收机可实时生成时延多普勒图(delay Doppler map,DDM),CYGNSS观测数据已在物理海洋学数据分发存档中心(https://podaac.jpl.nasa.gov/datasetlist)免费公开。本文选取2018-08~2019-12的L1级V3.0数据产品,包含经地理位置标定后的接收功率DDM(power_analog)及其他科学及工程参数,实验中仅选用与标定地表有效反射率和数据质量控制(quality controll,QC)相关的参数。利用DDM质量标识符提取陆地观测数据,并通过标志位掩码对观测数据进行初步的质量控制,剔除黑体标定和异常数据[8]。此外,遵循已有反演方法中采用的经验QC标准[5],规定镜面反射点入射角小于60°、镜面点方向的天线增益大于0 dB、DDM的信噪比大于2 dB,以获取高质量的原始数据集。
1.2 SMAP数据本文使用SMAP提供的L3 V8.0土壤湿度数据产品(ID:SPL3SMP),由美国国家冰雪数据中心(https://nsidc.org/data/SPL3SMP)发布。以36 km×36 km的等面积多分辨率地球格网(equal-area scalable earth grid, version 2.0,EASE-Grid 2.0)作为空间基准,每日提供一个HDF文件,包含升降轨数据。本文仅使用推荐区域单通道反演算法获得的升降轨地表土壤湿度均值,有效区间为0.0 ~0.5 cm3/cm3。对散射信号进行地表植被和粗糙度衰减改正时,同样使用SMAP产品提供的植被光学深度(vegetation_opacity)和地表粗糙度参数(roughness_coefficient)的升降轨均值。
1.3 标定地表有效反射率在相干假设中,入射至地表的GNSS信号在陆地表面仅发生相干反射。去除双基地雷达几何和观测系统硬件的影响后[5],地表有效反射率Γ可标定为:
| $ \mathit{\Gamma}=\frac{(4 \pi)^2 P_{\mathrm{coh}}\left(R_{\mathrm{ts}}+R_{\mathrm{rs}}\right)^2}{\lambda^2 G_{\mathrm{r}} P_{\mathrm{t}} G_{\mathrm{t}}} $ | (1) |
式中,Pcoh为DDM的峰值功率,PtGt为发射机的等效全向辐射功率,Pt为GNSS卫星右旋圆极化导航信号的发射功率,Gt为发射机天线增益,Gr为接收机天线增益,λ为发射信号的载波波长,Rts和Rrs分别为发射机到地表反射点的距离及接收机到地表反射点的距离。标定方程中所使用的相关参数均可在CYGNSS产品文件中获得。有效反射率与镜面反射点处的信号入射角和地表介电常数有关,后者主要受到地表土壤湿度的影响。此外,陆地观测信号还会受到地表粗糙度、植被覆盖率等影响,标定的地表有效反射率还需进一步修正:
| $ {\mathit{\Gamma}}_{\mathrm{LR}}\left(m_{\mathrm{v}}, k \sigma, \tau\right)=\mathrm{e}^{-2 \tau \mathrm{sec} \theta} \mathrm{e}^{-(2 \cos \theta) 2 k \sigma} {\mathit{\Gamma}}\left(m_{\mathrm{v}}\right) $ | (2) |
式中,mv为地表土壤湿度,k为信号波数,σ为地表的均方根高度,τ为植被光学深度,θ为信号的入射角。式(2)等式右侧第一个指数项表示植被衰减改正,第二个指数项表示小尺度的地表粗糙度改正。
1.4 反演方法经验星载GNSS-R地表土壤湿度反演方法需要借助其他土壤湿度观测手段提供的地表参考土壤湿度。由于星载GNSS-R的镜面反射点伪随机分布,因此在数据预处理中,首先需要对有效反射率进行入射角改正[8],然后将标定的离散地表有效反射率投影到与SMAP产品相同的参考格网中。在格网化过程中,当同一格网像素内有效反射率的数量小于3时,剔除该格网像素数据;若数量大于3,则将有效反射率的均值作为格网点值。最后匹配当日的SMAP土壤湿度,完成反演数据的时空匹配。
反演方法主要分为以下2大类:
1) 统一法直接建模:该方法最先由Clarizia等[5]提出,通过经验三元线性回归模型,将格网的参考土壤湿度表示为与格网有效反射率、植被光学深度和地表粗糙度有关的函数:
| $ u=\mathit{\Gamma} \cdot a+b \cdot \tau+c \cdot \sigma+d $ | (3) |
式中,Γ为格网点的有效反射率,τ为植被光学深度,σ为地表的粗糙度系数。对回归后的残差进行分析后发现,其与植被光学深度和地表粗糙度仍然存在相关性。因此,建立反演残差关于植被光学深度和地表粗糙度的改正查找表(lookup table,LUT),进一步对不同植被光学深度和地表粗糙度区间的反演结果进行改正。
2) 单格网上直接建模:对地表有效反射率进行格网化前,首先利用式(2)对观测信号进行植被和粗糙度衰减改正,然后再逐格网对有效反射率和参考土壤湿度进行线性拟合:
| $ u_{(i, j)}=\mathit{\Gamma}_{(i, j)} \cdot a_{(i, j)}+b_{(i, j)} $ | (4) |
式中,Γ(i, j)为格网像素(i, j)处的时空平均有效反射率,a和b分别为单格网线性模型的斜率和截距。由介电常数模型和菲涅尔方程可知,土壤湿度和反射率为非线性关系,但实际情况中绝大部分地表的年土壤湿度变化范围有限,因此可直接使用线性回归模型。某一格网像素上参与建模的训练数据组数量少于5时,不进行建模。
上述2种建模方法中,统一建模实际获得的是一组模型系数(a、b、c、d)及相应的改正LUT。单格网模型则可以表示为矩阵形式:
| $ \boldsymbol{U}_{\mathrm{v}}^{\mathrm{GNSS-R}}=\boldsymbol{A} \mathit{\pmb{\Gamma}}_{\mathrm{griddedh}}+\boldsymbol{B} $ | (5) |
式中,A为不同格网像素处线性模型的斜率组成的矩阵,B为不同格网像素上线性模型的截距组成的矩阵。在进行模型预测时,投影后的格网有效散射率可以通过矩阵运算直接输出地表土壤湿度。
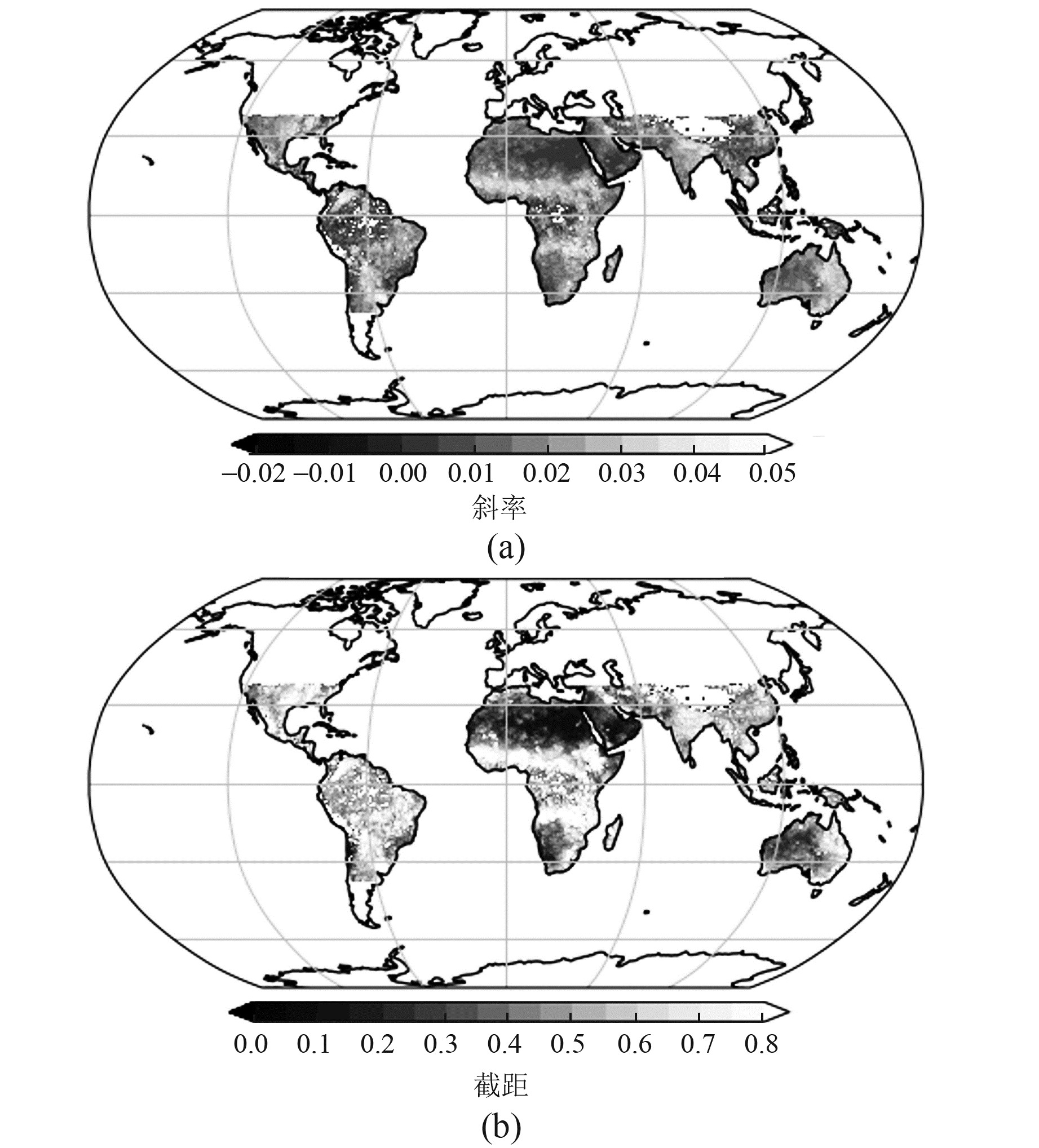
2 结果分析 2.1 土壤湿度反演结果对比经时空匹配获得研究时段的数据集后,使用2018-08~2019-07的数据集建立反演模型,剩余5个月的数据用于模型验证。图 1为利用训练集在单个格网上建立线性模型的斜率和截距空间分布。由图可见,不同空间区域上的建模结果存在一定差异,干旱地表的有效反射率较低、年土壤湿度的变化范围较小、地表土壤湿度水平相对稳定。标定得到的地表有效反射率的变化主要受到地表地形、观测噪声、代表误差的影响,干旱地区拟合得到的线性模型斜率小于潮湿地区,且模型截距趋向于0。年土壤湿度变化范围较大的地表上建立的线性模型斜率和截距均大于干燥地表,验证了反演模型的合理性。统一模型利用所有观测格网及其对应的土壤湿度、植被光学深度和地表粗糙度系数建立三元线性回归模型,得到的模型系数为a=0.375 1、b=0.446 5、c=0.19、d=-0.200 9。
|
图 1 单个格网直接建模时线性模型斜率和截距的空间分布 Fig. 1 The spatial distribution of slope and intercept of the linear model with the pixel-by-pixel retrieval model |
表 1(单位cm3/cm3)分别给出2种模型在训练集和测试集上的建模和预测精度。由表可见,2组模型建模和预测的平均偏差均接近于0 cm3/cm3,说明建模和预测结果中并未出现明显的系统性偏差,且建模精度和预测精度相当,也说明模型并未出现显著的过拟合现象。单格网模型的建模和预测精度均优于统一模型。测试集上,单格网直接建模预测的地表土壤湿度精度达0.056 cm3/cm3,而统一模型精度为0.081 cm3/cm3。
|
|
表 1 土壤湿度反演建模及预测结果的精度对比 Tab. 1 Comparison of the accuracy of soil moistureretrieval model fitting and prediction |
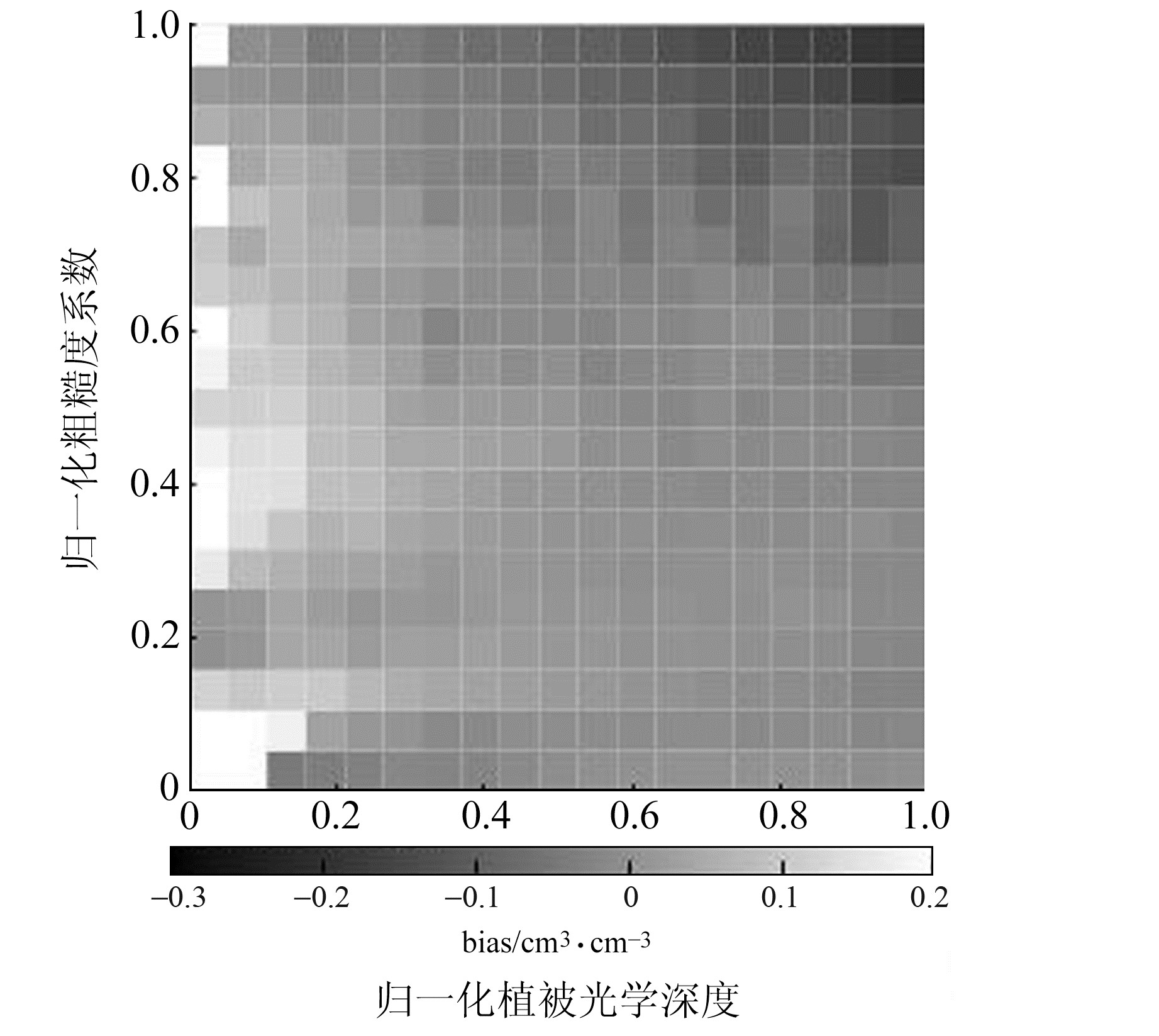
在统一建模反演方法中,除了对格网有效反射率、植被光学深度参数、地表粗糙度系数和参考土壤湿度进行三元线性回归拟合得到回归模型外,还会建立植被光学深度、地表粗糙度参数与反演残差的二维LUT,以进一步改正三元回归模型的估计偏差,本文建立的二维LUT对应的热图如图 2所示。由图可见,在植被光学深度较大的粗糙地表上,三元回归模型会出现明显的高估现象,而在植被稀疏地表上则会出现低估现象。利用二维LUT对模型输出进一步改正后,可以较好地解决潮湿地表上模型高估的问题,统一模型的建模精度从0.082 cm3/cm3提高到0.078 cm3/cm3,改善率为4.9%;预测精度由0.085 cm3/cm3提高到0.081 cm3/cm3,改善率为4.7%。
|
图 2 统一建模的改正LUT热图 Fig. 2 Heatmap of correction LUT within integrated retrieval model |
图 3(a)为统一模型估计的地表土壤湿度和参考SMAP土壤湿度的散点密度图。由图可见,模型预测值和参考值的相关系数为0.76,但整体上看,0~0.2 cm3/cm3区间范围内表现出低估的趋势,大于0.2 cm3/cm3的范围内表现出高估的趋势。图 3(b)为测试集上单格网反演模型估计的地表土壤湿度和参考SMAP土壤湿度的散点密度图,匹配的土壤湿度格网像素对的测试样本总数为2 501 775组。由图可见,模型预测值和参考值间的相关系数高达0.90,散点总体关于1 ∶1对角线对称分布,且回归线周围的分布密度最高,说明模型预测值和参考值之间的一致性较高。相较于统一模型,单格网模型的散点密度分布更加一致,在低、高土壤湿度水平下均表现出较好的性能,并未出现中高土壤湿度条件下统一模型高估的现象。

|
图 3 模型预测地表土壤湿度和SMAP参考土壤湿度的散点密度图 Fig. 3 Density scatter plot of retrieval model predicted soil moisture and SMAP soil moisture |
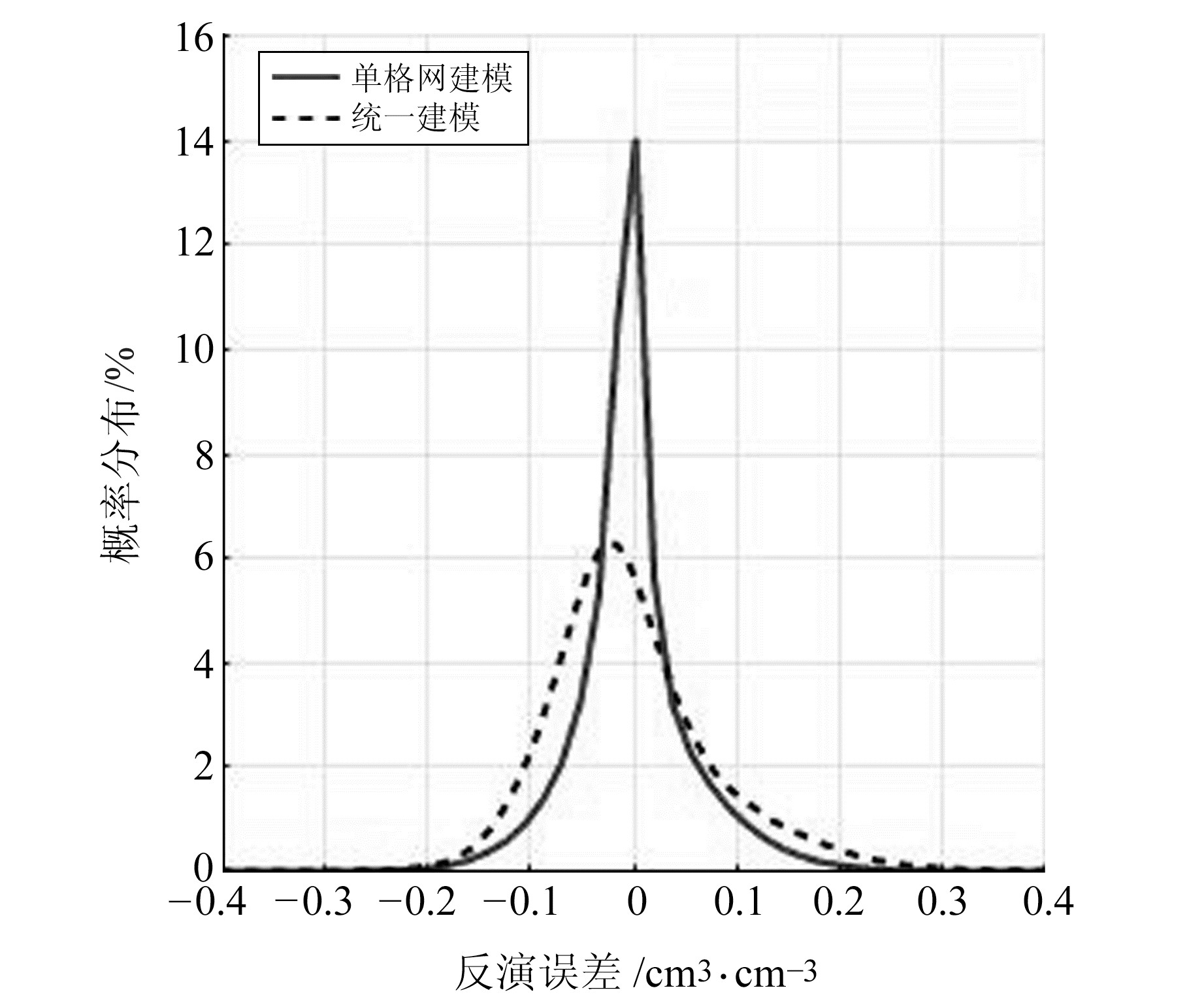
为进一步对比2种模型的估计差异,图 4为测试集上2种模型预测的地表土壤湿度误差概率密度分布曲线。由图可见,模型的反演偏差主要分布在-0.025~0.025 cm3/cm3之间,但单格网预测误差的分布更加集中,概率密度分布函数非常尖锐,统一模型的概率密度分布则更加分散。
|
图 4 反演误差的概率分布 Fig. 4 Probability density distribution of inversed deviation |
统计SMAP地表土壤湿度的月概率密度分布可以发现,多数陆地地表的土壤湿度小于0.1 cm3/cm3,且多数地表土壤湿度的年变化差异很小。根据不同格网的训练和测试数据分布可知,大多数格网中低土壤湿度条件下的数据占多数,在地表土壤湿度水平较低且变化很小的区域,观测信号更易受地表地形、观测噪声的影响,因此等权线性回归建立的统一反演模型失真较为严重,同时三元回归也不能很好地估计植被和地表粗糙度的影响。而在单个格网建模时,植被覆盖和地表地形特征的空间差异影响会相应减小,因此单格网建模的反演精度要优于统一建模。
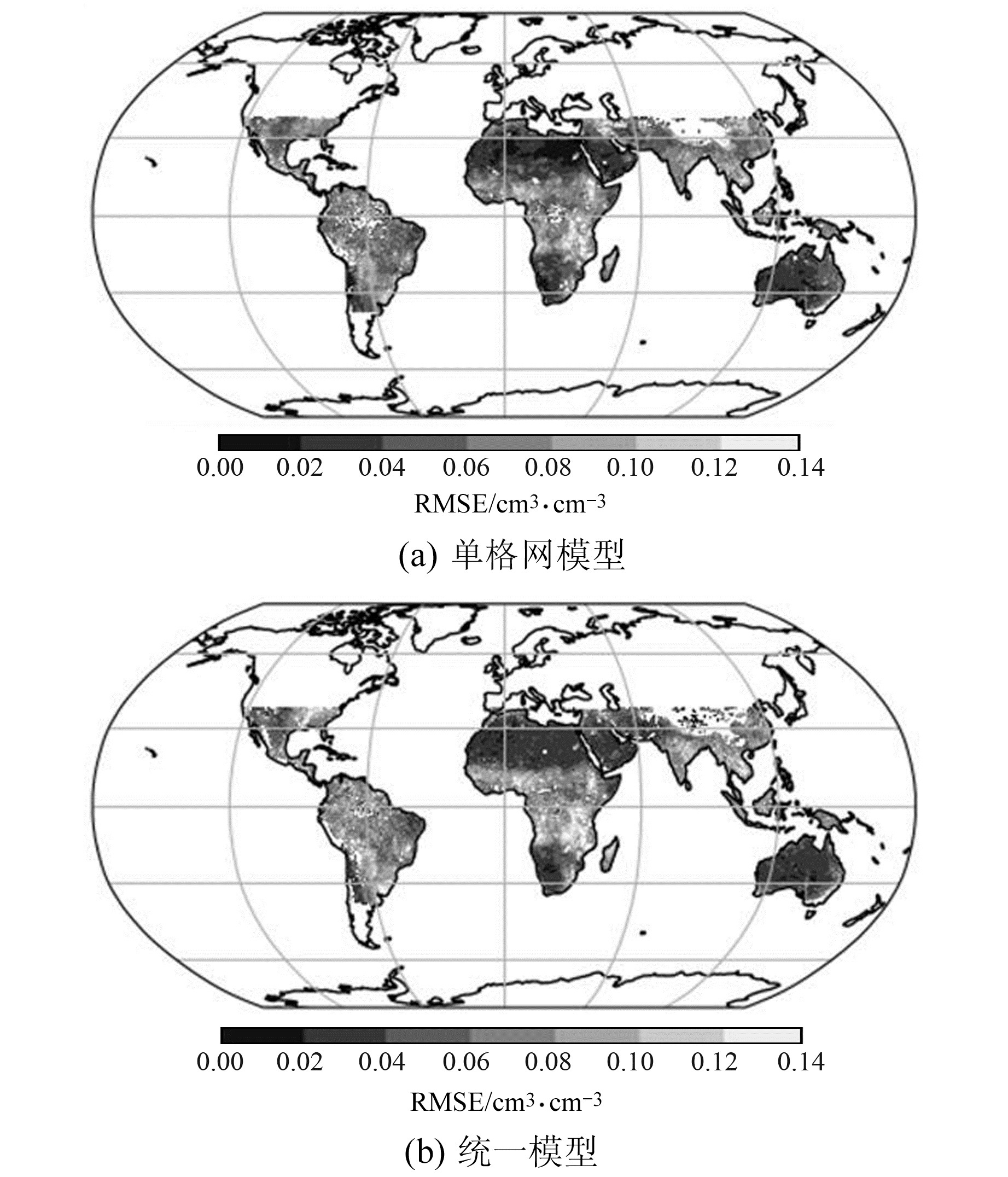
2.2 反演误差的时空分布反演误差的时空分布特征可以很好地反映反演模型的特征和性能。图 5为测试数据集不同格网像素处2组模型预测的地表土壤湿度均方根误差RMSE的空间分布。由图可见,绝大多数地表土壤湿度的反演精度优于0.06 cm3/cm3,仅有少数地区(如非洲中部地区及海岸线附近区域)存在相对较大的反演误差,这很可能由该地区的季节性洪水导致。同时,反演误差的分布也符合地表土壤湿度的空间分布特征,从侧面进一步验证了模型的可靠性。对比2组模型结果可知,统一模型在干燥地表和潮湿内陆水体边缘的反演精度较单格网模型下降明显。
|
图 5 单格网模型和统一模型反演地表土壤湿度的RMSE空间分布 Fig. 5 Spatial distribution of RMSE from the pixel-by-pixel retrieval model and integrated model |
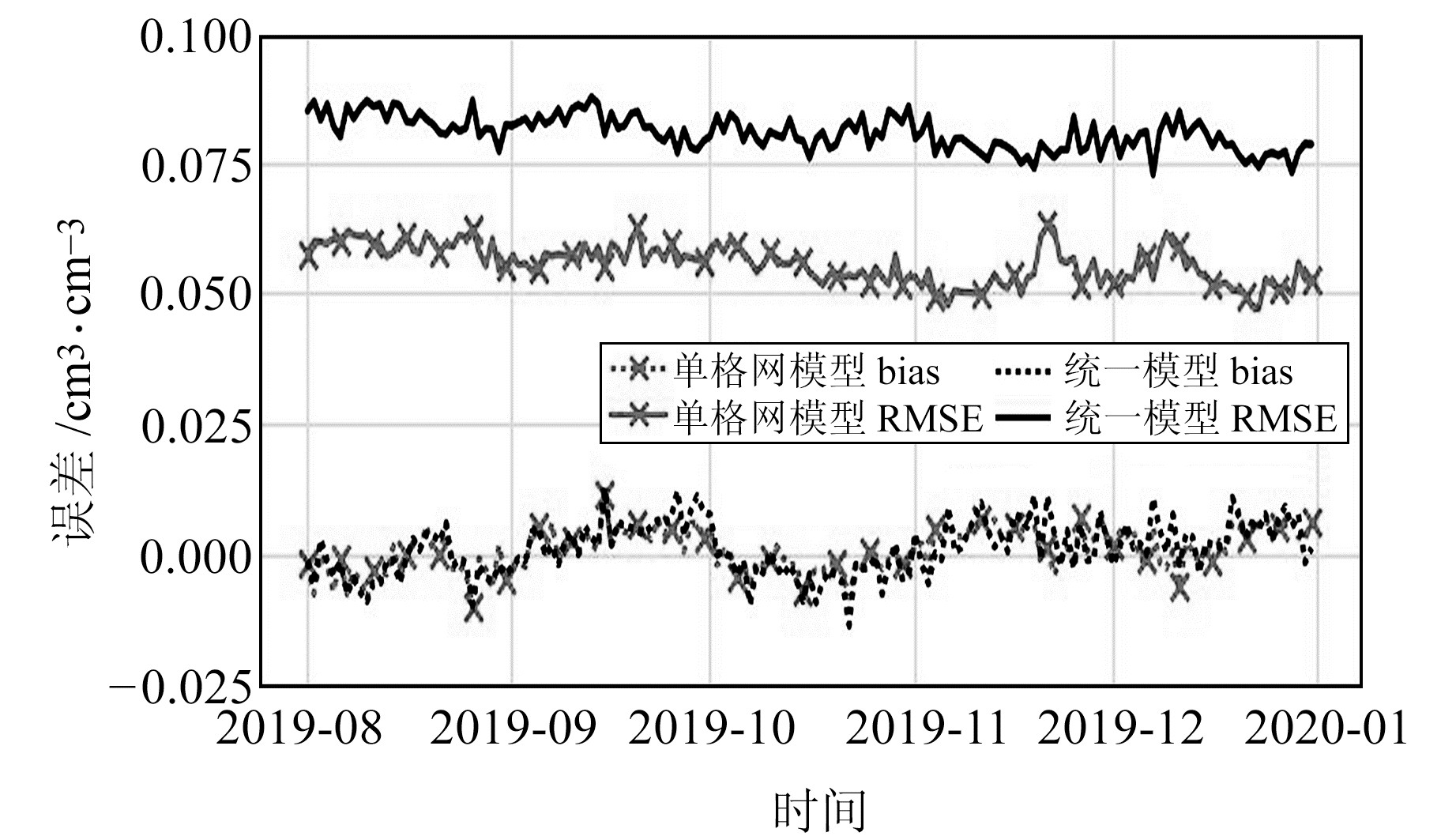
图 6为2种模型反演的地表土壤湿度单日统计的平均偏差和RMSE。由图可见,2种模型预测结果的单日平均偏差在0.0 cm3/cm3附近波动,说明模型估计结果未出现较为明显的系统性偏差。其中,统一建模预测土壤湿度单日的平均RMSE在0.08 cm3/cm3左右波动,而单格网模型则可以维持在0.06 cm3/cm3以下。本文建立的模型向后预测5个月仍未出现估计精度下降的趋势,表明预测模型具有极高的时域稳定性。
|
图 6 土壤湿度反演模型估计误差的时间序列 Fig. 6 Time series of estimation errors of soil moisture inverion model |
本文对比分析2种星载GNSS-R经验时空平均土壤湿度反演方法的性能,选取2018-08~2019-12的CYGNSS L1 V3.0数据进行实验。结果表明,星载GNSS-R反演结果与SMAP参考土壤湿度具有较好的一致性。单格网建模可以更好地顾及地表特征的空间差异,反演精度优于统一建模,在测试集上单格网建模反演土壤湿度RMSE为0.056 cm3/cm3,统一模型RMSE为0.081 cm3/cm3。同时,2种模型均具有较好的时域稳定性,反演模型一旦建立就可以进行长期的地表土壤湿度预测。
| [1] |
Babaeian E, Sadeghi M, Jones S B, et al. Ground, Proximal and Satellite Remote Sensing of Soil Moisture[J]. Reviews of Geophysics, 2019, 57(2): 530-616 DOI:10.1029/2018RG000618
(  0) 0) |
| [2] |
Egido A, Paloscia S, Motte E, et al. Airborne GNSS-R Polarimetric Measurements for Soil Moisture and Above-Ground Biomass Estimation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(5): 1 522-1 532 DOI:10.1109/JSTARS.2014.2322854
(  0) 0) |
| [3] |
Camps A, Park H, Pablos M, et al. Sensitivity of GNSS-R Spaceborne Observations to Soil Moisture and Vegetation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(10): 4 730-4 742 DOI:10.1109/JSTARS.2016.2588467
(  0) 0) |
| [4] |
Chew C, Shah R, Zuffada C, et al. Demonstrating Soil Moisture Remote Sensing with Observations from the UK TechDemoSat-1 Satellite Mission[J]. Geophysical Research Letters, 2016, 43(7): 3 317-3 324 DOI:10.1002/2016GL068189
(  0) 0) |
| [5] |
Clarizia M P, Pierdicca N, Costantini F, et al. Analysis of CYGNSS Data for Soil Moisture Retrieval[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(7): 2 227-2 235 DOI:10.1109/JSTARS.2019.2895510
(  0) 0) |
| [6] |
Yan Q Y, Huang W, Jin S, et al. Pan-Tropical Soil Moisture Mapping Based on a Three-Layer Model from CYGNSS GNSS-R Data[J]. Remote Sensing of Environment, 2020, 247: 111 944 DOI:10.1016/j.rse.2020.111944
(  0) 0) |
| [7] |
Dong Z N, Jin S G. Evaluation of the Land GNSS-Reflected DDM Coherence on Soil Moisture Estimation from CYGNSS Data[J]. Remote Sensing, 2021, 13(4): 570 DOI:10.3390/rs13040570
(  0) 0) |
| [8] |
Lei F N, Senyurek V, Kurum M, et al. Quasi-Global Machine Learning-Based Soil Moisture Estimates at High Spatio-Temporal Scales Using CYGNSS and SMAP Observations[J]. Remote Sensing of Environment, 2022, 276: 113 041 DOI:10.1016/j.rse.2022.113041
(  0) 0) |
| [9] |
Chew C C, Small E E. Soil Moisture Sensing Using Spaceborne GNSS Reflections: Comparison of CYGNSS Reflectivity to SMAP Soil Moisture[J]. Geophysical Research Letters, 2018, 45(9): 4 049-4 057 DOI:10.1029/2018GL077905
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43

