大气折射效应是指无线电波在大气中的传播路径与速度发生变化的现象,具体可分为电离层折射和对流层折射2大部分:电离层折射可利用多频观测值组合进行有效消除;而对流层折射具有非色散性,是制约GNSS[1]、VLBI[2]、InSAR[3]等空间大地测量技术精度的难点问题。对流层大气折射误差的主要修正算法有射线追踪法、映射函数法等,其中精度最高的是射线追踪法,其原理是沿电磁波传播路径对大气折射率和微分矢量长度的乘积进行积分[4]。由于大气折射率精度对最终修正效果有直接影响,因此本文重点研究如何提高大气折射率计算精度。
大气折射率的计算方法主要有直接探测法和模型法2种,直接探测法首先直接测量待求空间位置的大气温度、气压、湿度等气象参数,然后利用相关公式[5]计算大气折射率;模型法是建立任意高度与特定位置(如地面)间的折射率关系式,利用大量历史数据拟合出经验模型,如指数模型、双指数模型、ITU-R指数模型、Hopfield模型等。直接探测法精度高,但代价较大、时空分辨率有限;模型法精度虽不及直接探测法,但使用更为方便、适用性更强。
对流层大气的非色散性和水汽时空分布的随机性限制了传统折射率模型的精度:线性模型仅在1 km高度以下的区域与观测结果呈现出较好的一致性[6];指数模型的系数是由统计得到的均值,不能很好地反映各地区大气折射率的变化情况[7];Hopfield模型假定大气温度随高度的递减值为常数,会引入一定的模型误差。
基于此,本文利用BP神经网络对探空数据进行拟合,以中国境内96个观测站2016~2018年3 a的探空数据为训练集、2019年数据为测试集,建立新的大气折射率模型。为验证模型效果,将其与指数、ITU-R指数、双指数、Hopfield模型进行对比分析。
1 大气折射率模型 1.1 大气折射率对流层大气对电磁波信号传播的影响一般用大气折射指数n来表示,定义为无线电波在真空和介质中传播速度的比值。由于大气折射指数n的值接近于1,因此通常用折射率N表示大气折射指数n:
| $ N=(n-1) \times 10^6 $ | (1) |
式中,N可以分解为干项Nh和湿项Nw,并表示为大气压强P、温度T、水汽压e的函数[5]:
| $ \left\{\begin{array}{l} N=N_{\mathrm{h}}+N_{\mathrm{w}} \\ N_{\mathrm{h}}=k_1 \frac{P}{T} \\ N_{\mathrm{w}}=k_2^{\prime} \frac{e}{T}+k_3 \frac{e}{T^2} \end{array}\right. $ | (2) |
式中,k1=77.689,k2=71.295 2,k2′=k2-k1
根据某位置的气象数据,可利用式(2)计算出该处的大气折射率。但受条件限制,通常仅基于地面气象数据获得地面折射率,若想获得空间内任意处的大气折射率,需要借助经验模型,包括指数模型、ITU-R指数模型、双指数模型、Hopfield模型等。
1.2 指数模型采用负指数模型预测大气折射率,即[7]
| $ N=N_0 \exp (-c \cdot h) $ | (3) |
式中,N0为地面大气折射率,c为折射率衰减率,h为高程。通过拟合低纬度地区0~9 km海拔高度的数据可得c=0.16[7]。
1.3 ITU-R指数模型ITU-R指数模型中的折射率衰减率c是与大气折射率有关的特征高度H的倒数,即
| $ N=N_0 \exp \left(-\frac{h-h_0}{H}\right) $ | (4) |
式中,H=
将大气折射率N分为干项Nh和湿项Nw,分别用2个指数模型表示干项和湿项折射率分布,即双指数模型,公式[8]如下:
| $ \left\{\begin{array}{l} N_{\mathrm{h}}=N_{\mathrm{h} 0} \exp \left(-\frac{h}{H_{\mathrm{h}}}\right) \\ N_{\mathrm{w}}=N_{\mathrm{w} 0} \exp \left(-\frac{h}{H_{\mathrm{w}}}\right) \\ H_{\mathrm{h}}=\frac{\alpha}{N_{\mathrm{h} 0} \times 10^{-6}} P_0(m) \\ H_{\mathrm{w}}=\frac{\alpha}{N_{\mathrm{w} 0} \times 10^{-6}}\left(\frac{\beta}{T_0}+\gamma\right) e_0(m) \end{array}\right. $ | (5) |
式中,T0、P0、e0分别为地面温度、压强和水汽压,α=0.002 566 24,β=5 850.46,γ= -16.055 6。
1.5 Hopfield模型Hopfield模型又称双四次方模型,公式如下:
| $ \left\{\begin{array}{l} N_i=N_{i 0}\left(\frac{H_i-h}{H_i-h_0}\right)^4, i=\mathrm{h} / \mathrm{w}, h \leqslant H_i \\ N_i=0, i=\mathrm{h} / \mathrm{w}, h>H_i \end{array}\right. $ | (6) |
式中,Hh=40.136+0.148 72t0,为干项等效高度;Nw=11,为湿项等效高度。
2 方法与数据 2.1 大气折射率BP模型BP神经网络是一种多层前馈神经网络,主要特点为信号前向传递、误差反向传播,通常由3层结构组成。本文建立BP1_h、BP2_h、BP3_h三种干折射率模型与BP1_w、BP2_w、BP3_w三种湿折射率模型,网络结构如图 1所示。其中,BP1_h、BP1_w输入参数包括地表气温(T0)、地表气压(P0)、地表湿度(RH0)、地表高程(H0)、待定点高程(H);BP2_h、BP2_w在BP1的基础上增加待定点纬度(B);BP3_h、BP3_w在BP2的基础上进一步增加待定点经度(L)。输出参数为折射率干项(Nh)或湿项(Nw),激活函数采用对数S形转移函数,用单隐含层结构表示,神经元个数为50。

|
图 1 BP神经网络结构 Fig. 1 Structure of BP neural network |
本文从美国国家海洋和大气管理局地球系统研究实验室提供的无线电探空数据库(http://ruc.noaa.gov/raobs/)中选取中国境内96个探空站2016~2019年4 a的实测数据。数据为FSL格式,包含测站经纬度、高程、探空气球释放时间以及地表至40 km高度范围内多个层面上的气温、气压、露点温度、风速等信息。
水汽压和相对湿度是模型中的必要参数,但气象探空数据中仅给出露点温度,因此水汽压需利用BUCK模型和露点温度Td计算得到:
| $ e=6.1121 \times \exp \left(\frac{17.502 \times T_{\mathrm{d}}}{240.97+T_{\mathrm{d}}}\right) $ | (7) |
相对湿度RH采用下式计算得到[9]:
| $ R_H=\frac{e}{E_{\mathrm{s}}} \times 100 $ | (8) |
式中,Es为饱和水汽压,可通过Goff-Gratch模型[9]得到:
| $ \begin{array}{c} \lg E_{\mathrm{s}}=10.759\;47 \times\left(1-\frac{T_1}{T}\right)-5.028 \times \lg \frac{T_1}{T}+ \\ \text { 1. } \left.504\;75 \times 10^{-4} \times\left[1-10^{-8.296\;9 \times\left(\frac{T_1}{T}-1\right.}\right)\right]+ \\ 4.287\;3 \times 10^{-4} \times\left[10^{4.769\;55} \times\left(1-\frac{T_1}{T}\right)-1\right]+ \\ 0.786\;14 \\ \end{array} $ | (9) |
式中,T1为水的三相点温度(273.16 K)。该模型已被世界气象组织WMO规定为计算饱和水汽压的推荐公式。
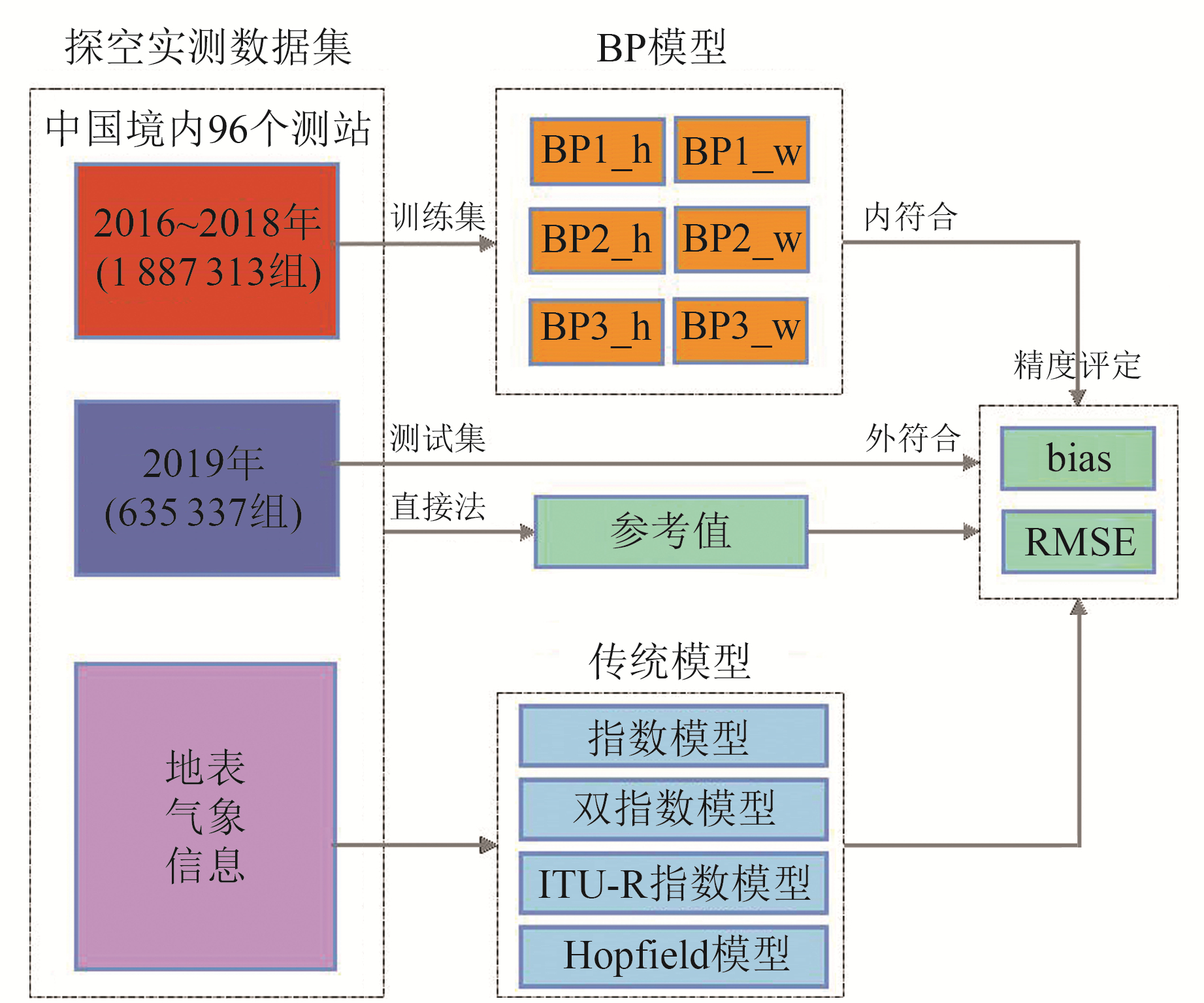
2.3 实验步骤实验技术路线如图 2所示,具体步骤如下:
|
图 2 技术路线图 Fig. 2 Technology roadmap |
1) 利用中国区域2016~2018年1 887 313组探空实测数据,根据式(2)计算大气折射率,组成训练集。
2) 设置学习率为0.1、训练次数为1 000、收敛误差为0,对3种BP模型进行训练。使用的CPU为AMD Ryzen 54 600 H with Radeon Graphics 3.00 GHz,RAM 16 GB,训练时长约为2 h,所获得的模型大小约80 MB。对1 887 313组数据进行预测并评定内符合精度,消耗内存约721 MB,计算用时小于1 s。
3) 利用中国区域2019年635 337组探空实测数据,根据式(2)计算大气折射率,作为BP模型的测试集。
4) 将BP模型的训练集和测试集中的地表气象信息全部输入传统模型中。
5) 将探空数据计算出的大气折射率作为参考值,评价各模型精度。
3 结果分析 3.1 误差评估方法采用偏差bias和均方根误差RMSE作为精度评价指标,具体计算公式为:
| $ \text { bias }=\frac{1}{K} \sum\limits_{i=1}^K\left(N_{\mathrm{m}}^i-N_{\mathrm{s}}^i\right) $ | (10) |
| $ \mathrm{RMSE}=\sqrt{\frac{1}{K-1} \sum\limits_{i=1}^K\left(N_{\mathrm{m}}^i-N_{\mathrm{s}}^i\right)^2} $ | (11) |
式中,Nmi、Nsi分别为大气折射率的模型计算值和利用探空数据计算的参考值。
3.2 BP模型精度分析利用训练集与测试集数据分别进行内符合与外符合精度评定,结果如表 1、表 2所示。由表可见,内符合方面,各模型的bias均较小且无明显差异;BP3模型的干、湿折射率RMSE均最小,其中BP3_h的RMSE比BP1_h、BP2_h分别降低0.116、0.051,BP3_w的RMSE比BP1_w、BP2_w分别降低0.227、0.009。外符合方面,各模型(尤其是湿折射率)的bias均大于内符合精度的bias;BP3模型的干、湿折射率RMSE均最小,其中BP3_h的RMSE比BP1_h、BP2_h分别降低0.087、0.026,BP3_w的RMSE比BP1_w、BP2_w分别降低0.229、0.013。在输入参数中增加纬度B后,BP2_h、BP2_w的RMSE比BP1_h、BP1_w分别降低3.9%、3.8%;进一步增加经度L后,BP3_h、BP3_w比BP2_h、BP2_w分别降低1.7%、0.2%。由此说明,纬度和经度均是干、湿折射率的影响因素,且纬度的影响大于经度,其中干折射率受经度影响更大,而湿折射率受经度影响较小。
|
|
表 1 BP神经网络内符合精度统计 Tab. 1 Internal accord accuracy statistics in BP neural network |
|
|
表 2 BP神经网络外符合精度统计 Tab. 2 External accord accuracy statistics in BP neural network |
各BP模型外符合精度的地理分布如图 3所示,圆的半径和颜色分别代表各站点的RMSE和bias。由图可见,3种BP_h模型在全国范围内均呈现出较高精度,无明显地理差异;但BP_w模型呈现出一定的东西部差异,西部、北部精度明显高于东部、南部,说明模型的湿折射率误差可能受到气候条件(尤其是水汽含量)的影响。

|
图 3 3种BP神经网络模型外符合精度的地理分布 Fig. 3 Geographical distribution of external accord accuracy of three BP neural network models |
双指数模型和Hopfield模型的干湿折射率精度如表 3所示,由于指数模型、ITU-R指数模型只输出总折射率,故未统计。各传统模型及本文最佳BP模型(BP3_h+BP3_w,以下总称为BP3)的总折射率精度如表 4所示。为方便比较,将数据集按照BP训练集(2016~2018年)和BP测试集(2019年)分别进行统计。
|
|
表 3 传统模型干湿折射率精度 Tab. 3 Wet and dry refractivity accuracy of traditional models |
|
|
表 4 各模型总折射率精度 Tab. 4 Total refractivity accuracy of each model |
由表 3可知,双指数和Hopfield模型的干折射率精度均高于湿折射率;Hopfield的干折射率精度明显高于双指数,但二者的湿折射率精度较为接近。双指数模型的干湿折射率bias均较大,但符号相反且数值较为接近。由表 4可知,指数模型精度最低,远不如其他3种模型;双指数模型总折射率bias在传统模型中最小,但RMSE与ITU-R指数模型相当。综合表 1~4可知,Hopfield模型的干、湿、总折射率RMSE均优于其他传统模型;BP3模型精度高于Hopfield模型,在BP训练集和测试集中,干折射率RMSE分别降低54.2%、50.3%,湿折射率RMSE分别降低16.9%、13.6%。与指数、ITU-R指数、双指数、Hopfield模型相比,BP3模型总折射率的RMSE分别降低69.8%、33.1%、31.9%、16.8%。
各模型在BP测试集上的总折射率精度分布如图 4所示,由于指数模型bias过大,因此采用与其他图不同的颜色范围表示。由图可见,各传统模型均存在较为明显的系统偏差,且不同模型呈现出不同的地理空间分群现象。BP3在各站点的精度分布明显更均匀,且西北地区与青藏高原各站点的总折射率RMSE得到了显著改善。

|
图 4 各模型总折射率精度的地理分布 Fig. 4 Geographical distribution of total refractivity accuracy of each model |
图 5为2019-06-01东部、中部、青藏高原、西北区域4个代表性站点的各模型误差随高度变化的剖面。由图可见,传统模型误差的系统性较强,随高度变化较为剧烈;BP3模型误差趋于偶然性,随高度的波动远小于传统模型。由此说明,相比于传统模型,本文训练得到的BP模型整体精度更高,在纵向剖面上更加均匀,能够在整个对流层高度范围内维持较高精度。

|
图 5 代表性站点误差垂直剖面图 Fig. 5 Vertical profile of error for representative sites |
1) 传统模型中,指数模型精度最低,Hopfield模型精度最高;ITU-R指数模型、双指数模型精度相当。3种BP模型中,BP2_h、BP2_w精度相对于BP1_h、BP1_w有明显提升,说明纬度是影响大气折射率的重要因素;BP3_h相对于BP2_h的精度提升幅度明显大于BP3_w相对于BP2_w的精度提升幅度,说明经度对干折射率影响较大,而对于湿折射率的影响较小。
2) 大气折射率是与大气压、温度、湿度和空间位置有关的复杂函数,难以采用传统模型进行有效拟合。本文提出的BP神经网络模型可以更好地表征这种非线性关系,整体精度优于传统模型,且在地理空间和纵向剖面上的误差分布也更加均匀。
| [1] |
杨飞, 郭际明, 李弈韬, 等. GPT3模型估计对流层产品精度检验与分析[J]. 大地测量与地球动力学, 2021, 41(11): 1 123-1 126 (Yang Fei, Guo Jiming, Li Yitao, et al. Accuracy Test and Analysis on the Tropospheric Products Derived from GPT3 Model[J]. Journal of Geodesy and Geodynamics, 2021, 41(11): 1 123-1 126)
(  0) 0) |
| [2] |
姜君, 宋淑丽, 周伟莉. 对流层经验模型在中国VLBI站上的优化分析[J]. 大地测量与地球动力学, 2020, 40(3): 231-235 (Jiang Jun, Song Shuli, Zhou Weili. Optimization Analysis of Tropospheric Delay Empirical Models on VLBI Sites in China[J]. Journal of Geodesy and Geodynamics, 2020, 40(3): 231-235)
(  0) 0) |
| [3] |
祝杰, 李瑜, 王坦, 等. 重轨星载InSAR形变监测中一种改进的大气延迟相位校正方法[J]. 大地测量与地球动力学, 2020, 40(11): 1 164-1 169 (Zhu Jie, Li Yu, Wang Tan, et al. An Improved Atmospheric Phase Delay Correction Method in Spaceborne Repeat-Track InSAR Monitoring[J]. Journal of Geodesy and Geodynamics, 2020, 40(11): 1 164-1 169)
(  0) 0) |
| [4] |
郭际明, 章迪, 史俊波, 等. 利用射线追踪法分析三种典型对流层映射函数在中国区域的精度[J]. 武汉大学学报: 信息科学版, 2015, 40(2): 182-187 (Guo Jiming, Zhang Di, Shi Junbo, et al. Using Ray-Tracing to Analyse the Precision of Three Classical Tropospheric Mapping Functions in China[J]. Geomatics and Information Science of Wuhan University, 2015, 40(2): 182-187)
(  0) 0) |
| [5] |
Zhang D, Guo J M, Fang T Y, et al. TMF: A GNSS Tropospheric Mapping Function for the Asymmetrical Neutral Atmosphere[J]. Remote Sensing, 2021, 13(13): 2 568 DOI:10.3390/rs13132568
(  0) 0) |
| [6] |
胡冉冉, 赵振维, 林乐科, 等. 近地面1 km高度处折射率梯度与地面气象参数统计关系的研究[J]. 电波科学学报, 2020, 35(6): 896-901 (Hu Ranran, Zhao Zhenwei, Lin Leke, et al. The Statistical Relationship between Refractivity Gradient in the Lowest 1 km near the Ground and Ground Meteorological Parameters[J]. Chinese Journal of Radio Science, 2020, 35(6): 896-901)
(  0) 0) |
| [7] |
陈雅颂, 汪晓银. 光电测量信息大气折射误差修正的数学模型研究[J]. 激光杂志, 2021, 42(8): 73-77 (Chen Yasong, Wang Xiaoyin. Study on Mathematical Model of Atmospheric Refraction Error Correction of Photoelectric Measurement Information[J]. Laser Journal, 2021, 42(8): 73-77)
(  0) 0) |
| [8] |
王旭良, 戴正旭, 陈红英. 一种基于海上探空气象数据的大气折射率模型[J]. 飞行器测控学报, 2015, 34(1): 36-41 (Wang Xuliang, Dai Zhengxu, Chen Hongying. An Atmospheric Refractivity Model Based on Maritime Radiosonde Data[J]. Journal of Spacecraft TT&C Technology, 2015, 34(1): 36-41)
(  0) 0) |
| [9] |
李得宴, 杨维芳, 高志钰, 等. 不同饱和水汽压模型对GNSS反演可降水量的影响分析[J]. 全球定位系统, 2020, 45(6): 55-63 (Li Deyan, Yang Weifang, Gao Zhiyu, et al. Analysis of Influence of Different Saturated Water Vapor Pressure Models on GNSS Inversion Precipitable Water[J]. GNSS World of China, 2020, 45(6): 55-63)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


