2. 九江市测绘地理信息有限公司,江西省九江市濂溪大道798号,332005;
3. 湖北科技学院资源环境科学与工程学院,湖北省咸宁市咸宁大道88号,437100
大气加权平均温度Tm是GNSS水汽反演过程中的关键参数,可将天顶湿延迟(zenith wet delay, ZWD)转换成大气可降水量(precipitable water vapor, PWV)[1]。Tm模型分为2类:需要气象参数的Tm模型和无需气象参数的Tm模型(非气象参数模型)。Bevis等[2]采用线性回归分析方法建立了著名的Bevis模型;姚宜斌等[3]按纬度建立了全球分段Tm-Ts关系模型,其精度明显高于Bevis模型;于胜杰等[4]研究发现,Bevis模型计算的中国区域Tm在不同高度上呈线性变化,由此建立按高度分段顾及偏差改正的Tm模型,其精度相较于Bevis模型有明显提高。
为开展极端天气条件下的实时监测与短期预报,需要构建非气象参数模型[5]。朱海等[6]研究发现,Tm与纬度具有一定的相关性,且具有年周期与半年周期,由此按纬度分段建立了顾及气候差异的Tm模型,其精度优于Bevis模型。已有诸多研究表明,Tm受高程的影响较为强烈[7]。由于Tm在垂直方向上的变化远大于水平方向[8],且大气再分析资料的格网点高程通常与GNSS站、探空站等所处高程不同,因此需要利用Tm垂直递减率模型对其进行改正。崔进业等[9]、谢劭峰等[10]在考虑Tm在垂直方向上随高度的变化关系后,建立区域Tm温度递减率模型,经高程改正后的Tm精度有较大提升;姚宜斌等[11]建立顾及非线性高程归算的Tm模型,显著提升了Tm在垂直方向上的归算效果;Zhang等[12]、黄良珂等[13]构建顾及垂直递减率函数的中国区域Tm模型,该模型在地形起伏较大的中国地区具有良好的性能。尽管上述模型在特定区域内精度较高,具有一定的优越性,但不适用于全球范围内的Tm计算。Yao等[14]在全球范围内使用统一的Tm垂直递减率进行高程改正,建立全球Tm模型,但单一的垂直递减率会在地形起伏复杂的地区产生较大的Tm误差。
由于已有全球Tm模型未对Tm进行垂直改正,或使用统一的垂直递减率模型对Tm进行垂直改正,未考虑垂直递减率在不同地区的周期特性,无法满足全球区域实时高精度Tm的获取。因此为了能够将再分析资料格网点的Tm数据精确插值到用户位置上,同时也为构建全球区域高精度Tm垂直递减率模型,本文利用2014~2017年ERA5大气再分析资料,通过计算格网点分层Tm得到垂直递减率,并对其进行时空特性分析。
1 数据来源及计算原理 1.1 数据来源ERA5大气再分析资料(https://apps.ecmwf.int/datasets/data/interim-full-daily)是欧洲中期天气预报中心ECMWF第五代全球气候再分析数据集,可提供逐小时的地表参数和等压分层数据,包括气压、温度、比湿等气象参数,水平分辨率为0.25°×0.25°,垂直分辨率为37层。ERA5数据能提供较为齐全的高分辨率地表数据及分层数据,是进行大气科学研究和对流层模型构建的重要数据源,有望在未来得到广泛应用。本文选取2014~2017年全球区域的ERA5大气再分析资料作为数据源。
1.2 计算原理利用探空站分层资料或大气再分析分层资料积分计算Tm,其积分计算表达式为[15]:
| $ T_m=\frac{\int_{h_{\mathrm{b}}}^{h_{\mathrm{t}}}(e / T) \mathrm{d} H}{\int_{h_{\mathrm{b}}}^{h_{\mathrm{t}}}\left(e / T^2\right) \mathrm{d} H}=\frac{\sum\left(e_i / T_i\right) \Delta H_i}{\sum\left(e_i / T_i^2\right) \Delta H_i} $ | (1) |
式中,e为水汽压,T为温度,ei为第i层大气的平均水汽压,Ti为第i层大气的平均温度,ΔHi为第i层大气的厚度,ht、hb分别为积分的最顶层高度和最底层高度。
由于全球范围内地形差异明显,不同地区高程变化较大,导致大气再分析资料格网点高程与用户高程之间存在较大差异。同时Tm在垂直方向上的变化远大于水平方向,因此需要对再分析资料提供的Tm数据进行垂直改正。已有研究表明,分层格网Tm数据与高程之间具有近似一次线性变化的关系[13]。
为进一步深入分析Tm随高程的变化情况,在全球范围内选取位于海洋、陆地、高海拔、低海拔等不同纬度地区的9个具有代表性的ERA5再分析资料格网点((60°N、90°W)、(0°、90°W)、(60°S、90°E)、(60°N、90°E)、(0°、90°E)、(60°S、90°W)、(80°N、0°)、(85°S、135°W)、(20°S、20°W))2017-01-01的分层格网Tm数据和相应位势高数据进行分析,结果如图 1所示。

|
图 1 9个代表性ERA5再分析资料格网点Tm随高程的变化情况 Fig. 1 The variation of Tm with elevation from nine representative ERA5 reanalysis data grid points |
由图 1可见,全球范围内9个具有代表性的ERA5再分析资料格网点的分层格网Tm数据与高程之间具有近似一次线性变化的关系,分层格网Tm数据随高程的增加而逐渐减小。由拟合线斜率γ可知,不同地理位置的Tm随高程的变化速率差异较大。拟合线的斜率可代表Tm的垂直递减率,其计算公式为:
| $ T_m=\gamma \times \delta h+l $ | (2) |
式中,γ为Tm垂直递减率,δh为高程,l为常数项。由此可知,Tm垂直递减率γ是对Tm数据进行垂直改正的重要参数。
2 全球Tm垂直递减率时空特性分析为探究Tm垂直递减率在全球范围内随时间的变化特征,选取不同地理位置的4个代表性ERA5再分析资料格网点计算2014~2017年的Tm垂直递减率,得到2014~2017年的日均Tm垂直递减率时间序列。采用年周期和半年周期的余弦函数对Tm垂直递减率进行季节性拟合,并采用快速傅里叶变换分析其周期性,结果如图 2所示。

|
图 2 Tm垂直递减率的季节变化及其频谱分析结果 Fig. 2 Seasonal variation of Tm lapse rate and their spectral analysis results |
由图 2可见,全球范围内4个具有代表性的ERA5再分析资料格网点Tm垂直递减率均表现出一定的季节性变化。其中,位于赤道地区(0°,90°W)格网点的Tm垂直递减率较为集中,基本保持在-6 ~-5 K/km之间,且其年周期和半年周期相对较弱,主要原因是赤道附近地区各种气象参数变化相对平稳,Tm在赤道附近地区的季节性变化也较弱;位于南北半球高纬度地区((60°N,90°W)、(60°S,90°E))格网点的Tm垂直递减率变化范围相对较大,且均表现出明显的年周期和半年周期变化,主要原因是高纬度地区受气候的影响较大,使得Tm垂直递减率在高纬度地区表现出明显的季节性变化;位于低纬度地区(30°N,90°E)格网点的Tm垂直递减率同样表现出季节性变化,其变化范围介于赤道和高纬度地区之间。
由图 2可见,位于赤道地区格网点的Tm垂直递减率的年周期和半年周期相对较弱,其中半年周期变化较年周期更加显著;位于南北半球高纬度地区格网点的Tm垂直递减率的年周期和半年周期相对较强,其中半年周期变化弱于年周期;位于低纬度地区格网点的Tm垂直递减率表现出明显的年周期变化,但几乎未表现出半年周期变化,其年周期变化强于赤道但弱于高纬度地区。
为探究更精细的Tm垂直递减率时间的变化特征,同样选取上述格网点,计算2014~2017年的Tm垂直递减率,得到2014~2017年每个时刻的日均Tm垂直递减率时间序列。利用日周期的余弦函数对Tm垂直递减率进行拟合,并采用快速傅里叶变换分析其周期性,结果如图 3所示。

|
图 3 Tm垂直递减率的日变化及其频谱分析结果 Fig. 3 Daily variation of Tm lapse rate and their spectral analysis results |
由图 3可见,4个具有代表性的ERA5再分析资料格网点Tm垂直递减率均未表现出明显的周期性变化。其中,位于北半球高纬度地区的格网点表现出一定的日周期变化,该格网点位于北美大陆,说明该地区Tm垂直递减率在1 d中的变化较为规律;位于赤道上的格网点表现出一定的半日周期变化,但未表现出日周期变化,主要原因是该格网点位于赤道海洋区域,可能受到海洋气候的影响[16];位于南半球高纬度地区的格网点均未表现出日周期或半日周期变化,主要原因是该格网点靠近南极大陆,可能受到南极大陆恶劣天气的影响;位于低纬度地区的格网点的日周期和半日周期变化强于其他地区。总体上看,全球区域内Tm垂直递减率的日变化较弱。
由上述分析可知,Tm垂直递减率具有明显的季节性变化,但日变化较弱,且不同地区的变化规律具有一定的差异。为进一步分析Tm垂直递减率的年均值、年周期和半年周期振幅在全球范围内的分布情况,同时探究其日周期振幅的变化特性,计算全球范围内2014~2017年时间分辨率为1 h的Tm垂直递减率,并利用式(3)计算得到全球范围内所有格网点Tm垂直递减率的年均值、年周期振幅、半年周期振幅以及日周期振幅:
| $ \begin{array}{c} \gamma= \\ A_0+A_1 \cos \left(2 \pi \frac{\text { doy }}{365.25}\right)+A_2 \sin \left(2 \pi \frac{\text { doy }}{365.25}\right)+ \\ A_3 \cos \left(4 \pi \frac{\text { doy }}{365.25}\right)+A_4 \sin \left(4 \pi \frac{\text { doy }}{365.25}\right)+ \\ A_5 \cos \left(2 \pi \frac{\text { hod }}{24}\right)+A_6 \sin \left(2 \pi \frac{\text { hod }}{24}\right) \end{array} $ | (3) |
式中,γ为Tm垂直递减率,A0为Tm垂直递减率的年均值,(A1, A2)为Tm垂直递减率的年周期系数,(A3, A4)为Tm垂直递减率的半年周期系数,(A5, A6)为Tm垂直递减率的日周期系数,doy为年积日,hod为UTC时。利用2014~2017年全球所有格网点的Tm垂直递减率,通过最小二乘法求得各格网点的系数,最终获得全球范围内所有格网点Tm垂直递减率的年均值、年周期振幅、半年周期振幅和日周期振幅,结果如图 4所示。

|
图 4 全球ERA5再分析资料计算Tm垂直递减率的年均值、年周期振幅、半年周期振幅和日周期振幅分布 Fig. 4 The distribution of annual average value, annual cycle amplitude, semiannual cycle amplitude and daily cycle amplitude for Tm lapse rate calculated using global ERA5 reanalysis data |
由图 4可见,Tm垂直递减率在南北半球高纬度地区的年均值绝对值较小,说明Tm在该地区随高度的变化相对较小;在南北半球低纬度地区、青藏高原、北美洲西南部以及南美洲北部等部分海拔较高的区域,Tm垂直递减率的年均值绝对值较大,说明Tm在这些地区随高度的变化较为剧烈,Tm垂直递减率在高海拔地区的绝对值相对较大。总体上看,南北半球Tm垂直递减率年均值绝对值均随纬度的增加而逐渐减小,说明Tm垂直递减率与Tm类似,与纬度的相关性较强;Tm垂直递减率在北美洲北部、亚洲东北部和南部、南美洲中部、非洲中部和南部以及南半球高纬度地区,尤其在南极洲大陆等地区的年周期振幅值较大,南北半球中低纬度地区的海洋和沿海地区振幅值相对较小;Tm垂直递减率在格陵兰岛、北美洲南部、亚洲中部和西南部、非洲中部以及南极洲北部等地区的半年周期振幅值较大,在南北半球中低纬度地区的海洋和沿海地区仍表现出相对较小的振幅值;Tm垂直递减率的陆地区域日周期振幅大于海洋区域,由此可知,日周期振幅存在明显的海陆差异和地形差异。在Tm垂直递减率日周期振幅值相对较大的地区,Tm垂直递减率的年周期和半年周期振幅也相对较大,且远大于日周期振幅。在进行Tm垂直递减率建模时,若同时考虑年周期和日周期变化,则相对较小的日周期变化容易被相对较大的年周期变化湮没,因此在构建短期预报的Tm垂直递减率模型时,应将日周期较大的地区考虑在内。
2.1 Tm与纬度的相关性为进一步深入探究Tm垂直递减率与纬度的相关性,选取经度分别为25.00°E、90.25°E、179.75°W和89.75°W的4条经线,计算得到2017年4条经线上各格网点的年均Tm垂直递减率,结果如图 5所示。
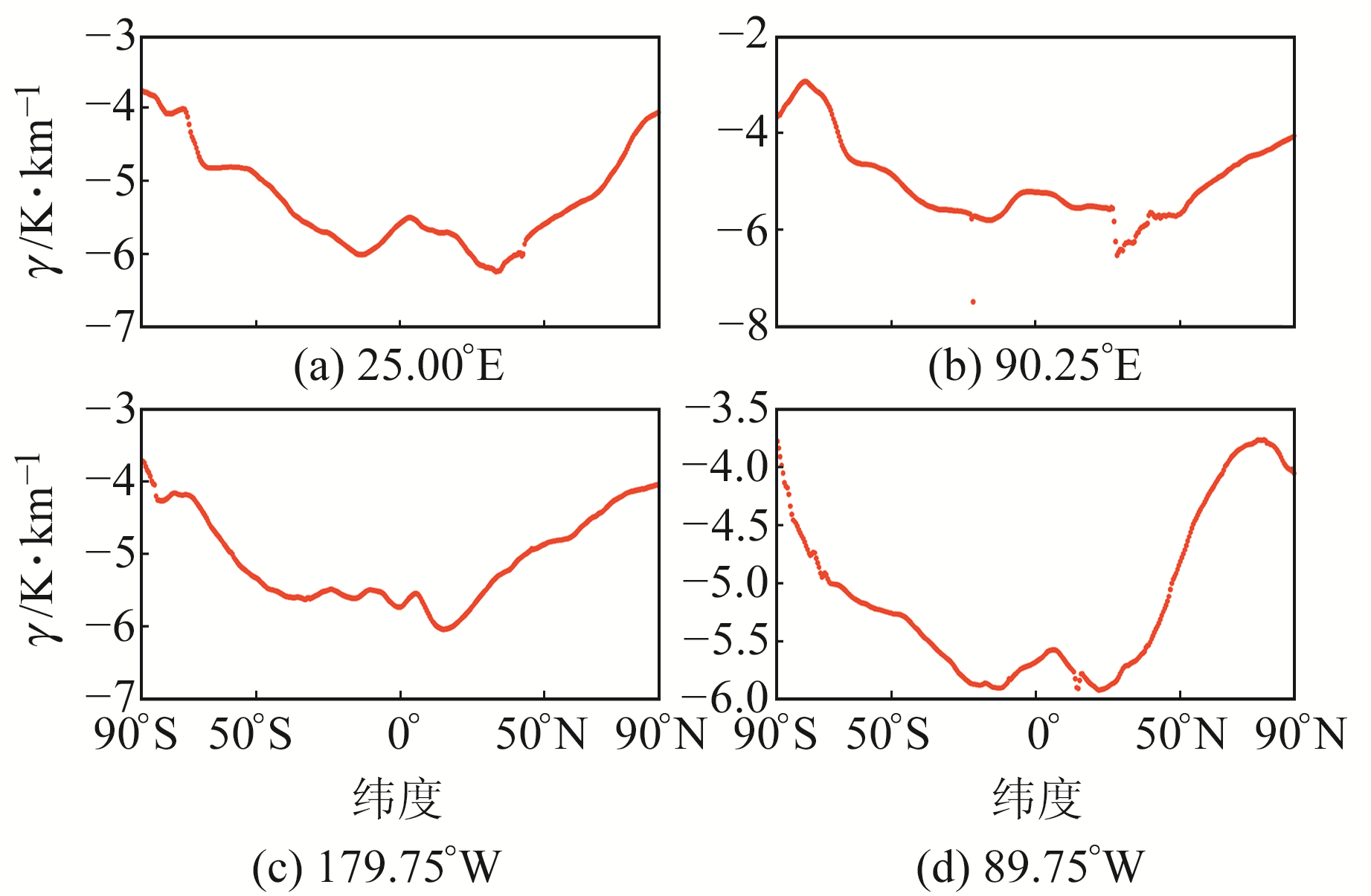
|
图 5 2017年Tm垂直递减率随纬度的变化 Fig. 5 Variation of Tm lapse rate with latitude in 2017 |
由图 5可见,4条经线的Tm垂直递减率与纬度具有较强的相关性,无论在北半球还是南半球,其绝对值均随纬度的增大而减小。其中,25.00°E和89.75°W经线上的Tm垂直递减率随纬度的变化较90.25°E和179.75°W更加剧烈,位于赤道附近的Tm垂直递减率变化幅度较小。Tm垂直递减率随纬度连续变化,但90.25°E经线上30°N附近区域出现间断现象,原因可能是该地区处于青藏高原地带,Tm垂直递减率会受到海拔剧烈变化的影响。Tm垂直递减率在25.00°E和89.75°W经线的赤道附近出现波动,可能是受到海陆差异的影响,Tm垂直递减率绝对值未呈现出随纬度增大而减小的连续变化现象。
2.2 Tm与经度的相关性为进一步深入探究Tm垂直递减率与经度的相关性,选取纬度为70.25°S、0.25°N、30.25°N和60.25°N的4条纬线,计算得到2017年4条纬线上各格网点的年均Tm垂直递减率,结果如图 6所示。
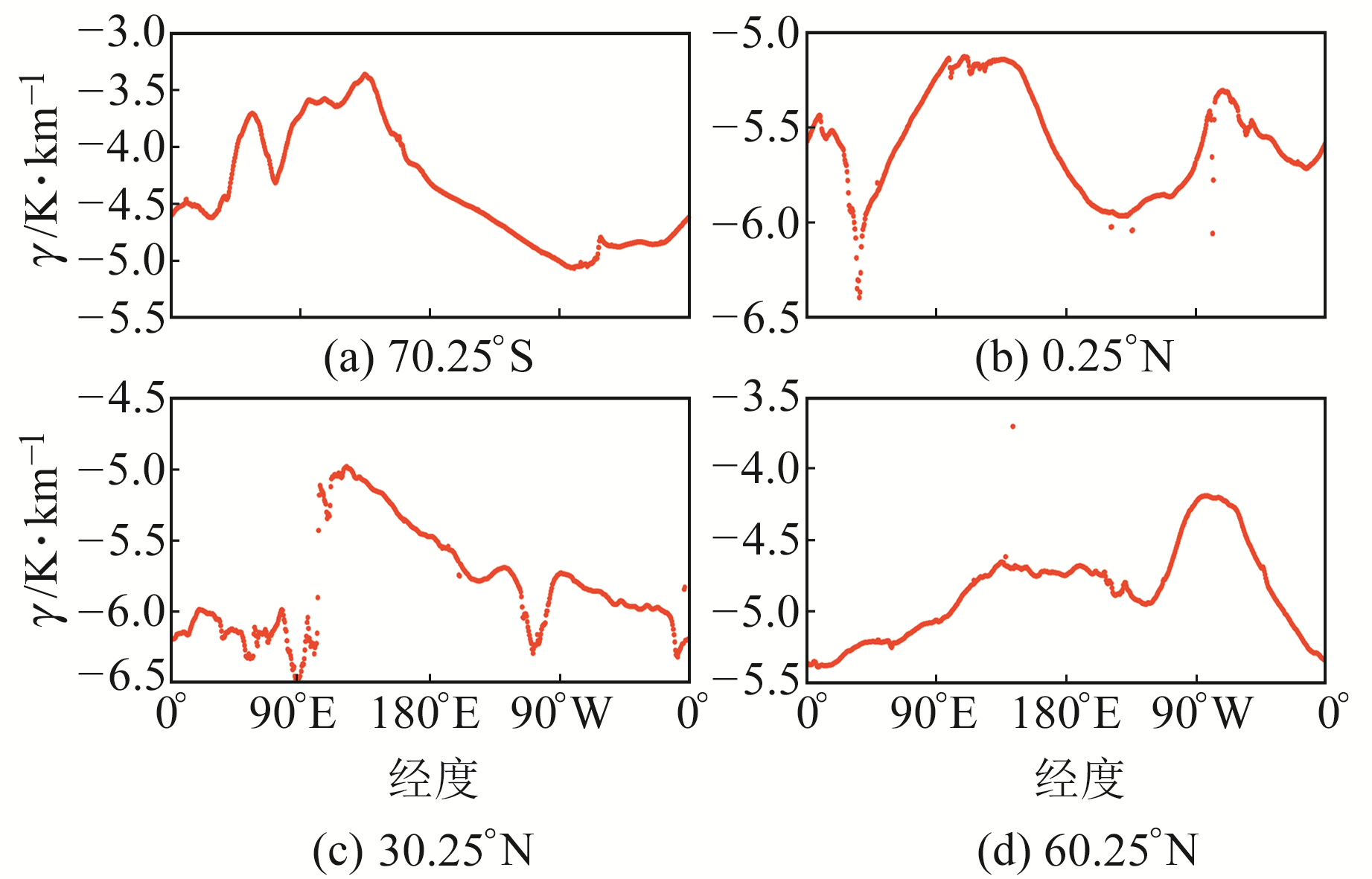
|
图 6 2017年Tm垂直递减率随经度的变化 Fig. 6 Variation of Tm lapse rate with longitude in 2017 |
由图 6可见,4条纬线上Tm垂直递减率未与经度呈现出相关性,而是出现上下波动的现象。在70.25°S和60.25°N的纬线上,Tm垂直递减率随经度的变化较为连续;而在0.25°N和30.25°N的纬线上均出现间断现象。0.25°N纬线上30°E附近为非洲大陆,而东西两侧均为海洋,Tm垂直递减率受到大陆的影响并未出现随经度连续变化的现象;30.25N纬线上90°E附近为青藏高原,东西两侧海拔较低,Tm垂直递减率受到海拔剧烈变化的影响并未出现随经度连续变化的现象。虽然位于赤道附近0.25°N纬线上的Tm垂直递减率出现上下波动的现象,但基本保持在-6~-5 K/km之间,变化幅度较其他纬度带较小,原因如前所述。
由图 5、图 6可知,Tm垂直递减率与纬度的相关性较强,但与经度的相关性较弱。为探究Tm垂直递减率随纬度的具体变化规律,选取经度为25.00°E、90.25°E、179.75°W和89.75°W的4条经线,计算2014~2017年4条经线上各格网点的日均Tm垂直递减率,结果如图 7所示。
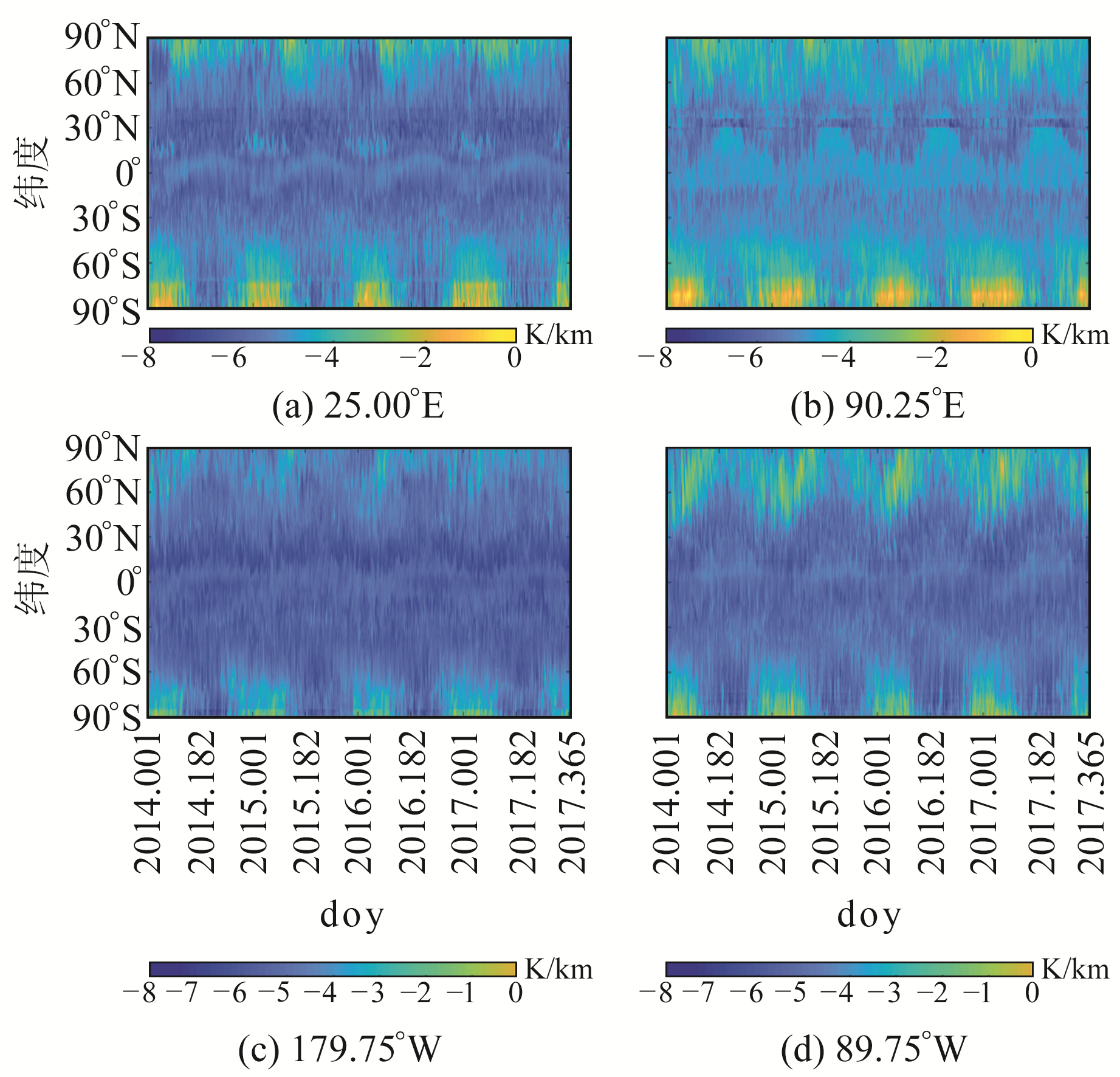
|
图 7 2014~2017年Tm垂直递减率随纬度的变化 Fig. 7 Variation of Tm lapse rate with latitude from 2014 to 2017 |
由图 7可见,Tm垂直递减率在赤道附近地区的绝对值较大,在高纬度地区的绝对值较小,在极地地区趋近于0。具体表现为Tm垂直递减率的绝对值由赤道向两极逐渐减小,即Tm在垂直方向上的变化剧烈程度随纬度的增加而减弱。同时,上述变化趋势在南北半球均存在一定的季节变化特征,具体表现为夏季的变化更加显著,冬季的变化弱于夏季。
为进一步分析Tm垂直递减率与经纬度的相关性,利用皮尔逊相关性分析法计算Tm垂直递减率与经纬度的相关系数,结果如表 1所示。
|
|
表 1 Tm垂直递减率与经纬度的相关系数 Tab. 1 Correlation coefficient between Tm lapse rate and latitude/longitude |
由表 1可见,Tm垂直递减率与纬度的相关系数为0.763,二者呈正相关,且相关性较高;与经度的相关系数为0.021,几乎无相关关系。因此在构建全球Tm垂直递减率模型时,需考虑Tm垂直递减率与纬度的相关性。
3 结语1) 全球范围内的Tm垂直递减率具有显著的年周期和半年周期,其中赤道附近周期性变化幅度相对较小,低纬度和中高纬度地区周期性变化幅度相对较大,日周期变化弱于年周期和半年周期。
2) Tm垂直递减率的年均值与纬度具有较强的相关性,年周期振幅、半年周期振幅具有一定的海陆差异,日周期振幅在全球范围内极小,且存在明显的海陆差异和地形差异。
3) Tm垂直递减率与纬度的相关性较强,其绝对值由赤道向两极逐渐减小,这种变化趋势在南北半球均存在一定的季节变化特征,具体表现为夏季变化更加显著,冬季变化弱于夏季。Tm垂直递减率与经度的相关性极小。
综上可知,在构建全球Tm垂直递减率模型时,需考虑年周期变化、半年周期变化及其与纬度的相关性。本文研究结果可为Tm垂直递减率模型的构建提供重要参考,在构建短期预报的Tm垂直递减率模型时,应将日周期较大的地区考虑在内。
| [1] |
王晓英, 戴仔强, 曹云昌, 等. 中国地区地基GPS加权平均温度Tm统计分析[J]. 武汉大学学报: 信息科学版, 2011, 36(4): 412-416 (Wang Xiaoying, Dai Ziqiang, Cao Yunchang, et al. Weighted Mean Temperature Tm Statistical Analysis in Ground-Based GPS in China[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 412-416)
(  0) 0) |
| [2] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research: Atmospheres, 1992, 97(D14): 15 787-15 801 DOI:10.1029/92JD01517
(  0) 0) |
| [3] |
姚宜斌, 张豹, 许超钤, 等. Tm-Ts的相关性分析及全球纬度相关的线性关系模型构建[J]. 科学通报, 2014, 59(9): 816-824 (Yao Yibin, Zhang Bao, Xu Chaoqian, et al. Analysis of the Global Tm-Ts Correlation and Establishment of the Latitude Linear Model[J]. Chinese Science Bulletin, 2014, 59(9): 816-824)
(  0) 0) |
| [4] |
于胜杰, 柳林涛. 水汽加权平均温度回归公式的验证与分析[J]. 武汉大学学报: 信息科学版, 2009, 34(6): 741-744 (Yu Shengjie, Liu Lintao. Validation and Analysis of the Water-Vapor-Weighted Mean Temperature from Tm-Ts Relationship[J]. Geomatics and Information Science of Wuhan University, 2009, 34(6): 741-744)
(  0) 0) |
| [5] |
Lu C, Li X, Ge M, et al. Estimation and Evaluation of Real-Time Precipitable Water Vapor from GLONASS and GPS[J]. GPS Solutions, 2016, 20(4): 703-713 DOI:10.1007/s10291-015-0479-8
(  0) 0) |
| [6] |
朱海, 黄观文, 张菊清. 顾及气候差异的区域加权平均温度模型: 以中国陕西为例[J]. 测绘学报, 2021, 50(3): 356-367 (Zhu Hai, Huang Guanwen, Zhang Juqing. A Regional Weighted Mean Temperature Model that Takes into Account Climate Differences: Taking Shaanxi, China as an Example[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(3): 356-367)
(  0) 0) |
| [7] |
Sun P, Wu S Q, Zhang K F, et al. A New Global Grid-Based Weighted Mean Temperature Model Considering Vertical Nonlinear Variation[J]. Atmospheric Measurement Techniques, 2021, 14(3): 2 529-2 542 DOI:10.5194/amt-14-2529-2021
(  0) 0) |
| [8] |
He C Y, Wu S Q, Wang X M, et al. A New Voxel-Based Model for the Determination of Atmospheric Weighted Mean Temperature in GPS Atmospheric Sounding[J]. Atmospheric Measurement Techniques, 2017, 10(6): 2 045-2 060 DOI:10.5194/amt-10-2045-2017
(  0) 0) |
| [9] |
崔进业, 马下平, 刘晓鹏. 香港地区顾及高度改正的加权平均温度模型[J]. 大地测量与地球动力学, 2020, 40(10): 1 022-1 026 (Cui Jinye, Ma Xiaping, Liu Xiaopeng. Weighted Mean Temperature Models with Vertical Adjustment for Hong Kong Region[J]. Journal of Geodesy and Geodynamics, 2020, 40(10): 1 022-1 026)
(  0) 0) |
| [10] |
谢劭峰, 李国弘, 周志浩. 华南地区温度递减率模型研究[J]. 测绘科学, 2020, 45(11): 123-129 (Xie Shaofeng, Li Guohong, Zhou Zhihao. Research on the Temperature Decline Rate Model in South China[J]. Science of Surveying and Mapping, 2020, 45(11): 123-129)
(  0) 0) |
| [11] |
姚宜斌, 孙章宇, 许超钤, 等. 顾及非线性高程归算的全球加权平均温度模型[J]. 武汉大学学报: 信息科学版, 2019, 44(1): 106-111 (Yao Yibin, Sun Zhangyu, Xu Chaoqian, et al. Global Weighted Mean Temperature Model Considering Nonlinear Vertical Reduction[J]. Geomatics and Information Science of Wuhan University, 2019, 44(1): 106-111)
(  0) 0) |
| [12] |
Zhang H X, Yuan Y B, Li W, et al. GPS PPP-Derived Precipitable Water Vapor Retrieval Based on Tm/Ps from Multiple Sources of Meteorological Data Sets in China[J]. Journal of Geophysical Research: Atmospheres, 2017, 122(8): 4 165-4 183 DOI:10.1002/2016JD026000
(  0) 0) |
| [13] |
黄良珂, 彭华, 刘立龙, 等. 顾及垂直递减率函数的中国区域大气加权平均温度模型[J]. 测绘学报, 2020, 49(4): 432-442 (Huang Liangke, Peng Hua, Liu Lilong, et al. An Empirical Atmospheric Weighted Mean Temperature Model Considering the Lapse Rate Function for China[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(4): 432-442)
(  0) 0) |
| [14] |
Yao Y B, Xu C Q, Zhang B, et al. GTM-Ⅲ: A New Global Empirical Model for Mapping Zenith Wet Delays onto Precipitable Water Vapour[J]. Geophysical Journal International, 2014, 197(1): 202-212 DOI:10.1093/gji/ggu008
(  0) 0) |
| [15] |
聂檄晨, 胡伍生, 朱明晨, 等. 中国区域加权平均温度的时空分析及模型研究[J]. 测绘科学, 2021, 46(2): 159-164 (Nie Xichen, Hu Wusheng, Zhu Mingchen, et al. Spatio-Temporal Analysis and Model Study of Regional Weighted Average Temperature in China[J]. Science of Surveying and Mapping, 2021, 46(2): 159-164)
(  0) 0) |
| [16] |
谢劭峰, 王义杰, 黄良珂, 等. 中国区域ERA5和MERRA-2再分析资料计Tm算的精度分析[J]. 大地测量与地球动力学, 2021, 41(8): 771-776 (Xie Shaofeng, Wang Yijie, Huang Liangke, et al. Accuracy Analysis of Tm Calculated by ERA5 and MERRA-2 Reanalysis Data over China[J]. Journal of Geodesy and Geodynamics, 2021, 41(8): 771-776)
(  0) 0) |
2. Jiujiang Surveying and Mapping Geographic Information Co Ltd, 798 Lianxi Avenue, Jiujiang 332005, China;
3. School of Resources and Environment Science and Engineering, Hubei University of Science and Technology, 88 Xianning Avenue, Xianning 437100, China
 2023, Vol. 43
2023, Vol. 43


