2. 中南林业科技大学土木工程学院,长沙市韶山南路498号,410004
在大地测量数据处理中,病态问题广泛存在于GNSS快速定位[1]、PolInSAR植被参数反演[2]、大地测量反演[3]等测绘领域中,严重影响参数估计的精度和可靠性。为解决病态模型带来的参数估计不稳定问题,通常采取2类方法进行处理:第一类是基于数学原理的方法,例如岭估计法、奇异值分解方法、TR法、主成分分析法等;第二类是将测量过程中获取的先验信息表示成等式、不等式或区间约束信息,将其加入平差模型中进行联合解算,以此降低模型的不适定性。第一类方法对较小的奇异值作处理,降低系数矩阵的条件数,但没有考虑参数的实际情况,解算出的估计值可能与观测实际不符;第二类方法虽然可以在降低模型不适定性的同时兼顾观测实际,但如何获取先验信息也是一个难题。因此,在先验信息不明确时,多采用第一类方法。
当TR法中的正则化矩阵为单位矩阵时,岭估计法等价于TR法。众多学者围绕测量领域中的正则化参数选择问题进行了研究:Wang等[4]提出一种不依赖数据拟合精度的A-最优设计方法来确定正则化参数,并将其应用到地震同震滑动分布反演中;林东方等[5]基于均方误差最小准则对L-曲线法进行二次优化,并将其应用到PolInSAR植被高反演实验中,改善正则化法的解算效果;Wang等[6]针对多源数据融合问题提出利用U曲线法确定正则化参数,利用判别函数最小化法确定观测数据中的相对权重比,该方法对2种及2种以上数据的融合效果较好。
由于TR法的解算效果过于依赖正则化参数的质量,且每种方法的优势与适用性各有不同,因此本文引入ITR法,将GCV法作为其迭代终止准则。ITR法是TR法的一种迭代改进方法,迭代过程中的正则化参数是预先设定的序列,解决了正则化参数选取困难的问题。
1 最小二乘病态问题最小二乘平差模型为:
| $ \boldsymbol{L}=\boldsymbol{A X}+\boldsymbol{e} \quad \text { 权阵 } \boldsymbol{P} $ | (1) |
式中,
在系数矩阵A无病态条件下,最小二乘解以及协方差为:
| $ \hat{\boldsymbol{X}}_{\mathrm{LS}}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{L} $ | (2) |
| $ \operatorname{cov}\left(\hat{\boldsymbol{X}}_{\mathrm{LS}}\right)=\sigma_0^2\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}\right)^{-1} $ | (3) |
式中,σ0为单位权中误差。对系数矩阵A进行奇异值分解,可得:
| $ \begin{array}{c} \boldsymbol{X}_{\mathrm{LS}}=\boldsymbol{A}^{+} \boldsymbol{L}=\boldsymbol{V S}^{+} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{L}=\sum\limits_{i=1}^n \frac{\boldsymbol{u}_i^{\mathrm{T}} \boldsymbol{L}}{\lambda_i} \boldsymbol{v}_i= \\ \sum\limits_{i=1}^n \frac{\boldsymbol{u}_i^{\mathrm{T}} \hat{\boldsymbol{L}}}{\lambda_i} \boldsymbol{v}_i+\sum\limits_{i=1}^n \frac{\boldsymbol{u}_i^{\mathrm{T}} \boldsymbol{e}}{\lambda_i} \boldsymbol{v}_i=\hat{\boldsymbol{X}}+\sum\limits_{i=1}^n \frac{\boldsymbol{u}_i^{\mathrm{T}} \boldsymbol{e}}{\lambda_i} \boldsymbol{v}_i \end{array} $ | (4) |
| $ \boldsymbol{D}\left(\hat{\boldsymbol{X}}_{\mathrm{LS}}\right)=\operatorname{tr}\left[\operatorname{cov}\left(\hat{\boldsymbol{X}}_{\mathrm{LS}}\right)\right]=\sigma_0^2 \sum\limits_1^n \frac{1}{\lambda_i^2} $ | (5) |
由式(4)右侧第二项可知,λi≈0使得观测误差被放大,导致最小二乘估计严重偏离真值。从式(5)可以看出,λi≈0使得方差被严重放大,此时的最小二乘解极不可靠。
2 标准Tikhonov正则化与迭代Tikhonov正则化标准Tikhonov正则化为:
| $ \min\limits _X\left\{\|\boldsymbol{L}-\boldsymbol{A} \boldsymbol{X}\|^2+\mu\|\boldsymbol{X}\|^2\right\} $ | (6) |
式(6)的解为:
| $ \boldsymbol{X}_\mu=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}+\mu \boldsymbol{I}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{L} $ | (7) |
经奇异值变换可得:
| $ \begin{array}{c} \boldsymbol{X}_\mu=\boldsymbol{V}\left(\boldsymbol{S}^{\mathrm{T}} \boldsymbol{S}+\mu \boldsymbol{I}\right)^{-1} \boldsymbol{S}^{\mathrm{T}} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{L} \\ \boldsymbol{X}_\mu=\sum\limits_{i=1}^n \boldsymbol{v}_i \cdot \frac{1}{\lambda_i^2+\mu} \cdot \lambda_i \cdot \boldsymbol{u}_i^{\mathrm{T}} \cdot \boldsymbol{L}= \end{array} $ | (8) |
| $ \sum\limits_{i=1}^n \boldsymbol{v}_i \cdot \frac{\lambda_i^2}{\lambda_i^2+\mu} \cdot \frac{1}{\lambda_i} \cdot \boldsymbol{u}_i^{\mathrm{T}} \cdot \boldsymbol{L} $ | (9) |
因此,
| $ \boldsymbol{X}_\mu=\boldsymbol{V} \boldsymbol{f}_\mu \boldsymbol{S}^{+} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{L}=\boldsymbol{A}_\mu^{+} \boldsymbol{L} $ | (10) |
式中,
标准Tikhonov正则化的缺点在于估计参数的质量过于依赖正则化参数μ的选择,当μ选择过大时,结果与原问题相差甚远;当μ选择过小时,系数矩阵的病态程度改善不明显,模型依然会出现高度不稳定的现象。基于此,引入迭代Tikhonov正则化法进行改进。
迭代Tikhonov正则化推导过程如下[7]:在数据处理理论中,观测值均带有误差,即观测值与真值之差:
| $ \boldsymbol{e}=\hat{\boldsymbol{L}}-\boldsymbol{L} $ | (11) |
式中,
| $ \hat{\boldsymbol{L}}=\boldsymbol{A} \hat{\boldsymbol{X}} $ | (12) |
式中,
| $ \boldsymbol{\delta}_k=\hat{\boldsymbol{X}}-\boldsymbol{X}_k $ | (13) |
式中,下标k为计算过程中的迭代次数。δk越小,求出的参数解越接近真值。由于实际应用中参数真值
| $ \boldsymbol{X}_k+\boldsymbol{h}_k \approx \boldsymbol{X}_k+\boldsymbol{\delta}_k=\hat{\boldsymbol{X}} $ | (14) |
| $ \boldsymbol{X}_{k+1}=\boldsymbol{X}_k+\boldsymbol{h}_k $ | (15) |
式中,Xk+1是在Xk基础上的一个改进近似值。
| $ \boldsymbol{r}_k=\boldsymbol{L}-\boldsymbol{A} \boldsymbol{X}_k $ | (16) |
| $ \hat{\boldsymbol{L}}=\boldsymbol{L}+e $ | (17) |
式中,rk为用第k次迭代解Xk求出的观测值误差向量,则有:
| $ \begin{array}{c} \boldsymbol{r}_k=\boldsymbol{L}-\boldsymbol{A} \boldsymbol{X}_k= \\ \hat{\boldsymbol{L}}-\boldsymbol{e}-\boldsymbol{A}\left(\hat{\boldsymbol{X}}-\boldsymbol{\delta}_k\right)=\boldsymbol{A} \boldsymbol{\delta}_k-\boldsymbol{e} \end{array} $ | (18) |
因此,δk的近似值hk可以通过求解如下最小二乘问题得到:
| $ \min\limits _{h \in R^n}\left\|\boldsymbol{A} \boldsymbol{h}-\boldsymbol{r}_k\right\|^2 $ | (19) |
同样,当系数矩阵病态时,对其添加正则化项:
| $ \min\limits _{h \in R^n}\left\|\boldsymbol{A} \boldsymbol{h}-\boldsymbol{r}_k\right\|^2+\mu_k\|\boldsymbol{h}\|^2 $ | (20) |
式(20)的解为:
| $ \boldsymbol{h}_k=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}+\mu_k \boldsymbol{I}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{r}_k $ | (21) |
| $ \begin{array}{c} \boldsymbol{X}_{k+1}=\boldsymbol{X}_k+\boldsymbol{h}_k= \\ \boldsymbol{X}_k+\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}+\mu_k \boldsymbol{I}\right)^{-1} \boldsymbol{A}^{\mathrm{T}}\left(\boldsymbol{L}-\boldsymbol{A} \boldsymbol{X}_k\right) \end{array} $ | (22) |
迭代Tikhonov正则化就是不断重复上述细化过程,求解参数解的最优近似值。
3 基于GCV的迭代Tikhonov正则化GCV函数[8]为:
| $ \begin{array}{c} G(\mu)=\frac{\left\|\left(\boldsymbol{I}-\boldsymbol{A} \boldsymbol{A}_\mu^{+}\right) \boldsymbol{L}\right\|^2}{\left[\operatorname{tr}\left(\boldsymbol{I}-\boldsymbol{A} \boldsymbol{A}_\mu^{+}\right)\right]^2}= \\ \frac{\left\|\left(\boldsymbol{I}-\boldsymbol{S} \boldsymbol{f}_\mu \boldsymbol{S}^{+}\right) \boldsymbol{U}^{\mathrm{T}} \boldsymbol{L}\right\|^2}{\left[\operatorname{tr}\left(\boldsymbol{I}-\boldsymbol{S} \boldsymbol{f}_\mu \boldsymbol{S}^{+}\right)\right]^2} \end{array} $ | (23) |
式中,
| $ \mu_{\mathrm{GCV}}=\arg \min\limits _{\mu}G(\mu) $ | (24) |
即使G(μ)为凸函数,其导数也可能非常小,因此最小化函数G(μ)可能会很复杂。当GCV函数变化较为平缓时,很难求得最小值。为避免求解复杂的极小化GCV函数,首先需要在迭代Tikhonov正则化中给定一个固定的序列{μk}。
令X0=0,则第一次迭代值X1为:
| $ \boldsymbol{X}_1=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}+\mu_0 \boldsymbol{I}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{L}=\boldsymbol{V} \boldsymbol{f}_{\mu_0} \boldsymbol{S}^{+} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{L} $ | (25) |
令φ1= fμ0,则有:
| $ \boldsymbol{X}_1=\boldsymbol{V} \boldsymbol{\varphi}_1 \boldsymbol{S}^{+} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{L} $ | (26) |
根据迭代Tikhonov正则化的定义,可以求得X2为:
| $ \begin{array}{c} \boldsymbol{X}_2=\boldsymbol{X}_1+\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}+\mu_1 \boldsymbol{I}\right)^{-1} \boldsymbol{A}^{\mathrm{T}}\left(\boldsymbol{L}-\boldsymbol{A} \boldsymbol{X}_1\right)= \\ \boldsymbol{X}_1+\boldsymbol{V} \boldsymbol{f}_{\mu_1} \boldsymbol{S}^{+} \boldsymbol{U}^{\mathrm{T}}\left(\boldsymbol{L}-\boldsymbol{A} \boldsymbol{X}_1\right)=\boldsymbol{V} \boldsymbol{\varphi}_1 \boldsymbol{S}^{+} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{L}+ \\ \boldsymbol{V}_{\mu_1} \boldsymbol{S}^{+} \boldsymbol{U}^{\mathrm{T}}\left(\boldsymbol{L}-\boldsymbol{A} \boldsymbol{X}_1\right)=\boldsymbol{V} \boldsymbol{\varphi}_1 \boldsymbol{S}^{+} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{L}+ \\ \quad \boldsymbol{V} \boldsymbol{f}_{\mu_1} \boldsymbol{S}^{+} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{L}+\boldsymbol{V} \boldsymbol{f}_{\mu_1} \boldsymbol{S}^{+} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{V} \boldsymbol{\varphi}_1 \boldsymbol{S}^{+} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{L} \end{array} $ | (27) |
由于A = USVT,因此有S = UTAV,上式第三项可改写成:
| $ \boldsymbol{V} \boldsymbol{f}_{\mu_1} \boldsymbol{S}^{+} \boldsymbol{S} \boldsymbol{\varphi}_1 \boldsymbol{S}^{+} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{L}=\boldsymbol{V} \boldsymbol{f}_{\mu_1} \boldsymbol{\varphi}_1 \boldsymbol{S}^{+} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{L} $ | (28) |
即
| $ \boldsymbol{X}_2=\boldsymbol{V}\left(\boldsymbol{\varphi}_1+\boldsymbol{f}_{\mu_1}\left(\boldsymbol{I}-\boldsymbol{\varphi}_1\right)\right) \boldsymbol{S}^{+} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{L} $ | (29) |
令
| $ \boldsymbol{X}_2=\boldsymbol{V} \boldsymbol{\varphi}_2 \boldsymbol{S}^{+} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{L} $ | (30) |
综上,可以得到基于GCV的迭代Tikhonov正则化为:
| $ \boldsymbol{X}_k=\boldsymbol{V} \boldsymbol{\varphi}_k \boldsymbol{S}^{+} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{L} $ | (31) |
| $ \left\{\begin{array}{l} \boldsymbol{\varphi}_1=\boldsymbol{f}_{\mu_0} \\ \boldsymbol{\varphi}_{k+1}=\boldsymbol{\varphi}_k+\boldsymbol{f}_{\mu_k}\left(\boldsymbol{I}-\boldsymbol{\varphi}_k\right) \end{array}\right. $ | (32) |
基于GCV法的迭代Tikhonov正则化ITR-GCV法步骤如下:
1) 给定序列
2)
3) 计算
4) 计算
5) 计算
6) 令
7)
Hilbert矩阵是经典的病态矩阵,定义为:
利用e ~ N (0, 1)模拟观测过程中的随机误差。令参数真值Xzhen=[1 ,1 ,1 ,1 ,1 ,1]T,模拟观测值为L = AX + e。分别采用以下6种方法进行计算:最小二乘法LS、截断奇异值分解法TSVD(截断参数k=0.1)、截断奇异值分解法TSVD(截断参数k=0.01)、Tikhonov正则化法L-曲线法TR-Lcurve、基于CGV的Tikhonov正则化法TR-GCV、基于GCV的迭代Tikhonov正则化法ITR-GCV(取μ0=0.5,μk=2×k,k=1, ⋯, 1 000)。
为比较6种方法的性能,本文进行50次随机模拟实验,计算每次实验的参数估值与真值之间的二范数,即
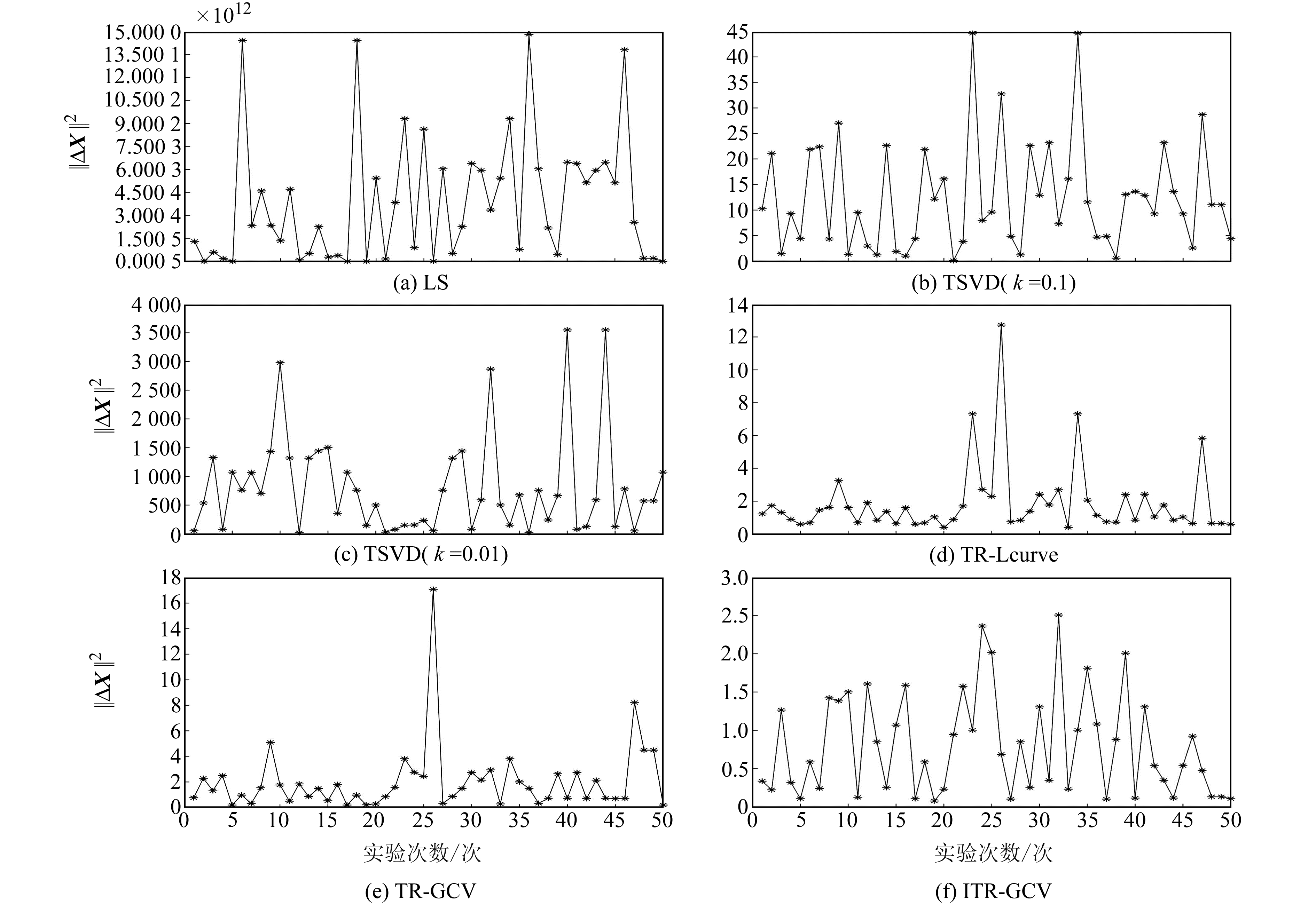
|
图 1 6种方法的计算结果 Fig. 1 Calculation results of six methods |
系数矩阵A的条件数为2.450 6×106,是一个严重病态矩阵。由图 1(a)可见,当系数矩阵病态时,最小二乘解已经严重失真,‖ΔX‖2最小值为7.242 2×108,最大值为1.481 7×1013,状态极不稳定。
由图 1(b)、(c)可见,截断奇异值分解法的解算质量取决于截断参数的选择。系数矩阵A的奇异值为[1.697 2 0.285 4 0.023 7 0.001 2 3.881 5×10-5 6.852 3×10-7]。当k=0.1时,相当于只保留了前2个奇异值包含的数据信息;当k=0.01时,相当于只保留了前3个奇异值包含的数据信息。根据条件数公式可知,条件数的数值为矩阵最大奇异值与最小奇异值之差。当k=0.1时,改善后矩阵的条件数为5.884 8;当k=0.01时,改善后矩阵的条件数为70.857 4。因此,TSVD法k=0.1时的效果优于k=0.01,但由于该方法删掉了系数矩阵中过多的小奇异值信息,因此其解算效果差于TR法。
由图 1(d)、(e)可见,TR法的解算效果优于LS法和TSVD法。50次模拟实验中,TR-Lcurve法和TR-GCV法的结果较好。
由图 1(f)可见,ITR-GCV解的残差范数始终在一个较小的范围内波动,相较于其他方法有更强的稳定性。迭代过程中的正则化参数预先给定,迭代次数为1 000,在1 000次以内均能收敛。该过程无需进行复杂的正则化参数求解,迭代求解的方式减弱了其对正则化参数的敏感程度和依赖性。
为进一步分析上述几种方法的稳定性与精度,对每一个估计值的均值
|
|
表 1 算例1的均值、标准差、均方根误差比较 Tab. 1 Mean, standard deviation, root mean square error comparison of example 1 |
由表 1可见,受到系数矩阵病态性的影响,最小二乘解严重失真,标准差和均方根误差较大,其参数估计的精度和稳定性较差。虽然TSVD法的精度有所改善,但在减弱模型病态性的同时也引入较大偏差;TR-Lcurve法和TR-GCV法虽然降低了病态性、减少了引入偏差的量,但2种方法过于依赖正则化参数的选择,结果较不稳定;ITR-GCV法通过迭代的方式改进TR法,其标准差和均方根误差均明显减小,采用该方法可以得到精度更高、稳定性更强的解。
4.2 算例2引用文献[9]中的GPS快速定位算例,历元采样间隔为2 s,观测卫星数为5个,利用4个历元的观测数据解算整周模糊度。未知参数X =[Δx Δy Δz N1 N2 N3 N4]T,其中Δx、Δy、Δz为基线向量的坐标改正数,N1、N2、N3、N4为整周模糊度参数。
系数矩阵为:
| $ \boldsymbol{A}=\left[\begin{array}{ccccccc} 0.271\;9 & 1.500\;8 & -0.604\;6 & 0.190\;3 & -0.190\;3 & 0 & 0 \\ 0.323\;4 & -1.707\;8 & 0.136\;9 & 0 & 0.190\;3 & -0.190\;3 & 0 \\ -0.612\;1 & 1.405\;1 & -1.402\;5 & 0 & 0 & 0.190\;3 & -0.190\;3 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0.321\;9 & -1.708\;5 & 0.136\;4 & 0 & 0.190\;3 & -0.190\;3 & 0 \\ -0.613\;1 & 1.404\;9 & -0.403\;1 & 0 & 0 & 0.190\;3 & -0.190\;3 \\ 0.150\;5 & -0.644\;3 & -0.082\;2 & 0 & 0 & 0 & 0.190\;3 \end{array}\right] $ | (33) |
已知未知参数真值Xzhen=[-2.256 4 -2.148 9 6.503 1 0 6 -5 -14]T。利用e ~ N (0, 1)模拟观测过程中的随机误差,从而模拟线性化后的常数向量L = AX + e。采用算例1中的6种方法分别进行计算。为避免数据的随机性,本文进行50次随机实验,计算出各个参数的均值、标准差、均方根误差,结果见表 2。
|
|
表 2 算例2的参数均值、标准差、均方根误差比较 Tab. 2 Mean, standard deviation, root mean square error comparison of example 2 |
根据表 2的平差结果,可以得到以下结论:
1) 系数矩阵条件数cond(A)=2.740 5×105,为严重病态矩阵。此时,最小二乘解严重失真,参数解不稳定。
2) 系数矩阵的奇异值为(5.662 1, 1.479 4, 0.762 4, 0.420 3, 0.034 9, 6.789 1×10-4, 2.093 6×10-4),分别选择2个不同的截断参数(k=1和0.5)进行TSVD求解。结果表明,TSVD法的标准差在6种方法中最小,稳定性最强,但其均方根误差较大,说明直接截去系数矩阵小奇异值的方法会引入过大的偏差,求解精度不高。
3) TR法的关键在于正则化参数μ的选择,实质上是通过引入一定量的偏差来降低参数估值的方差。μ的作用是平衡方差和偏差,既能最大程度降低估值的方差,也能控制偏差的量。从50次模拟实验的整体效果上看,在参数估值稳定性和精度方面,TR-GCV法选取的正则化参数优于TR-Lcurve法。
4) ITR-GCV法中取μ0=0.5, μk=0.3×k, k=1, ⋯, 1 000。ITR-GCV法的标准差和均方根误差均较小,稳定性和精度都有所提高。
5 结语本文引入迭代Tikhonov正则化法,并利用GCV作为其迭代终止准则。模拟实验和GPS快速定位实验表明,相较于传统方法,本文方法在参数估计的稳定性和精度上都有所改善。本文2次设定的迭代次数均为1 000,且实验过程中都能保证收敛。但本文给定的序列{μk}是关于k的一次函数,这与之前学者提出的{μk}是关于k的指数函数有所不同[7]。针对不同的测量问题以及不同的系数矩阵病态情形,如何选择正则化参数序列是接下来的研究重点。
| [1] |
朱亮亮. 病态问题理论研究及其在GNSS快速定位中的应用[D]. 桂林: 桂林电子科技大学, 2018 (Zhu Liangliang. Theoretical Research on Ill-Conditioned Problems and Its Application in Fast GNSS Positioning[D]. Guilin: Guilin University of Electronic Technology, 2018)
(  0) 0) |
| [2] |
林东方, 朱建军, 宋迎春. 顾及截断偏差影响的TSVD截断参数确定方法[J]. 测绘学报, 2017, 46(6): 679-688 (Lin Dongfang, Zhu Jianjun, Song Yingchun. Truncation Method for TSVD with Account of Truncation Bias[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(6): 679-688)
(  0) 0) |
| [3] |
王乐洋, 赵雄, 高华. 大地测量地震断层同震滑动分布反演的两步解法[J]. 武汉大学学报: 信息科学版, 2019, 44(9): 1 265-1 273 (Wang Leyang, Zhao Xiong, Gao Hua. A Two-Step Solution Method for the Co-Seismic Slip Distribution Inversion of Earthquake Faults in Geodesy[J]. Geomatics and Information Science of Wuhan University, 2019, 44(9): 1 265-1 273)
(  0) 0) |
| [4] |
Wang L Y, Gu W W. A-Optimal Design Method to Determine the Regularization Parameter of Coseismic Slip Distribution Inversion[J]. Geophysical Journal International, 2020, 221(1): 440-450 DOI:10.1093/gji/ggaa030
(  0) 0) |
| [5] |
林东方, 朱建军, 付海强, 等. 均方误差意义下的正则化参数二次优化方法[J]. 测绘学报, 2020, 49(4): 443-451 (Lin Dongfang, Zhu Jianjun, Fu Haiqiang, et al. Optimization of Regularization Parameter Based on Minimum MSE[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(4): 443-451)
(  0) 0) |
| [6] |
Wang L Y, Zhao X, Gao H. A Method for Determining the Regularization Parameter and the Relative Weight Ratio of the Seismic Slip Distribution with Multi-Source Data[J]. Journal of Geodynamics, 2018, 118: 1-10 DOI:10.1016/j.jog.2018.04.005
(  0) 0) |
| [7] |
Buccini A, Donatelli M, Reichel L. Iterated Tikhonov Regularization with a General Penalty Term[J]. Numerical Linear Algebra With Applications, 2017, 24(4)
(  0) 0) |
| [8] |
张慧. 求解线性离散不适定问题的改进Tikhonov算法[D]. 南京: 南京航空航天大学, 2015 (Zhang Hui. The Improved Tikhonov Algorithms for Solving Linear Discrete Ill-Posed Problems[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015)
(  0) 0) |
| [9] |
赵邵杰, 宋迎春, 李文娜. 利用不等式约束求解病态问题的新算法[J]. 北京测绘, 2021, 35(11): 1 366-1 373 (Zhao Shaojie, Song Yingchun, Li Wenna. A New Algorithm for Ill-Posed Problems with Inequality Constraints[J]. Beijing Surveying and Mapping, 2021, 35(11): 1 366-1 373)
(  0) 0) |
2. School of Civil Engineering, Central South University of Forestry and Technology, 498 South-Shaoshan Road, Changsha 410004, China
 2023, Vol. 43
2023, Vol. 43


