周跳探测作为全球卫星导航系统数据预处理中的重要组成部分,是进行高精度导航定位的必要操作。作为最常用的双频周跳探测方法,TurboEdit算法[1]联合MW组合法和GF(geometry-free)组合法,可克服单一组合存在的不足,具有探测效率高、灵活性强等优点。但该方法也存在低载噪比历元易发生周跳误检、探测阈值固定、易受高电离层延迟影响、拟合方式容易引入人为误差等局限性。目前已有许多研究在探测阈值的选取[2]和拟合方式[3-8]上对TurboEdit算法进行了改进。
北斗卫星导航系统BDS的周跳探测原理与全球定位系统GPS相似,但由于星座构成不同,BDS与GPS的周跳探测也存在差别,在GPS上具有良好性能的周跳探测方法无法直接应用到BDS上[9]。研究表明,BDS-2不同种类卫星的伪距观测值之间存在系统偏差[10],且该偏差与卫星高度角有关[11]。蔡成林等[12]将原有GF组合探测方法改进为相邻历元求差法后发现,BDS不同种类卫星GF组合观测值的变化范围不同,根据卫星种类选取阈值参数可更好地适应各种BDS卫星。
载噪比CNR是BDS定位的重要观测数据之一,也是衡量观测信号质量的重要指标,可用于评估信号测距精度。但在现有的周跳探测方法中,CNR数据未被有效利用。基于此,本文基于传统TurboEdit算法,在分析BDS不同种类卫星对周跳探测影响的基础上,提出一种基于载噪比加权的MW组合周跳探测模型,能够有效消除BDS之间的系统性偏差,提升BDS周跳的探测性能。
1 TurboEdit算法探测原理TurboEdit算法利用MW组合和GF组合联合探测周跳,可解决单一组合周跳探测中存在的不敏感周跳问题。
1.1 MW组合周跳探测载波相位观测值的宽巷组合减去伪距观测值的窄巷组合即可得到MW,其组合观测值LMW为:
| $ L_{\mathrm{MW}}=\frac{f_1 L_1-f_2 L_2}{f_1-f_2}-\frac{f_1 P_1+f_2 P_2}{f_1+f_2}=N_{\mathrm{WL}} \lambda_{\mathrm{WL}} $ | (1) |
式中,下标1、2分别对应BDS的2个频点f1、f2信号;Lk和Pk分别为载波相位和伪距观测值,单位均为m,其中Lk可表示为:
| $ L_k=\lambda_k \varphi_k $ | (2) |
式中,λk为频点fk的载波波长;φk为以周为单位的载波相位观测值。
式(1)中λWL为宽巷波长,可表示为:
| $ \lambda_{\mathrm{WL}}=c /\left(f_1-f_2\right) $ | (3) |
式(1)中NWL为宽巷模糊度,可表示为:
| $ N_{\mathrm{WL}}=N_1-N_2 $ | (4) |
式中,Ni为不同频点载波相位观测量的整周模糊度。宽巷模糊度NWL也可表示为:
| $ N_{\mathrm{WL}}=\varphi_1-\varphi_2-\frac{f_1 P_1+f_2 P_2}{\lambda_{\mathrm{WL}}\left(f_1+f_2\right)} $ | (5) |
当未发生周跳时,NWL应接近于常数并随机分布。在MW组合中使用式(6)和式(7)递推计算历元i的平均宽巷模糊度NWL(i)和均方根σ2(i),递推公式为:
| $ \begin{array}{l} \bar{N}_{\mathrm{WL}}(i)=\bar{N}_{\mathrm{WL}}(i-1)+ \\ \frac{1}{i}\left[N_{\mathrm{WL}}(i)-\bar{N}_{\mathrm{WL}}(i-1)\right] \end{array} $ | (6) |
| $ \begin{array}{c} \sigma^2(i)=\sigma^2(i-1)+ \\ \frac{1}{i}\left[\left(N_{\mathrm{WL}}(i)-\bar{N}_{\mathrm{WL}}(i-1)\right)^2-\sigma^2(i-1)\right] \end{array} $ | (7) |
当满足式(8)时,则确认历元i存在周跳:
| $ \left\{\begin{array}{l} \left|N_{\mathrm{WL}}(i)-\bar{N}_{\mathrm{WL}}(i-1)\right| \geqslant 4 \sigma(i-1) \\ \left|N_{\mathrm{WL}}(i+1)-N_{\mathrm{WL}}(i)\right| \leqslant 1 \end{array}\right. $ | (8) |
但当2个频点同时发生大小相等的周跳时,MW组合无法进行有效探测,因此需要采用GF组合联合MW组合的方式解决该问题。
1.2 GF组合周跳探测GF组合对2个频点同类型观测量数值作差,采用载波相位观测值和伪距观测值构建的GF组合数学模型为:
| $ L_{\mathrm{GF}}=L_1-L_2=\lambda_1 N_1-\lambda_2 N_2+\Delta I $ | (9) |
| $ P_{\mathrm{GF}}=P_2-P_1=\Delta I $ | (10) |
式中,LGF、PGF分别为载波相位和伪距的GF组合;ΔI为2个频点的电离层延迟差。由于伪距观测值中含有噪声,为消除噪声干扰,需要对伪距GF组合PGF进行多项式拟合生成QGF。对多项式进行拟合时,其阶数m=min[(N/100+1), 6], N为待拟合历元总数。GF组合构建的周跳探测模型为:
| $ \Delta L_{\mathrm{GF}}=L_{\mathrm{GF}}-Q_{\mathrm{GF}}=\lambda_1 N_1-\lambda_2 N_2 $ | (11) |
当满足式(12)时确认历元i存在周跳:
| $ \left\{\begin{array}{l} \left|\Delta L_{\mathrm{GF}}(i)-\Delta L_{\mathrm{GF}}(i-1)\right|>6\left(\lambda_2-\lambda_1\right) \\ \left|\Delta L_{\mathrm{GF}}(i+1)-\Delta L_{\mathrm{GF}}(i)\right|<1\left(\lambda_2-\lambda_1\right) \end{array}\right. $ | (12) |
虽然对PGF进行拟合生成QGF能够在一定程度上降低伪距观测噪声的影响,但多项式拟合涉及多项式类型、拟合次数、拟合长度、拟合阶数等人为因素,其检测效果仍然存在一定的局限性。
2 MW组合观测值特性分析TurboEdit算法中的MW组合可同时消除大气延迟和卫星钟差的影响,组合后的MW组合观测值只受多路径效应、观测噪声和硬件延迟的影响,可以在一定程度上反映多径路效应和硬件延迟的变化水平。当未发生周跳时,MW组合观测值接近于常数。但有关研究表明,BDS-2 IGSO卫星和MEO卫星的MW组合观测值不为常数,而是存在一个与高度角相关的系统偏差[11],因此TurboEdit算法无法有效应用于BDS-2中[9]。
由于接收机位置未知,数据预处理阶段无法计算卫星高度角,而载噪比与高度角具有极强的相关性且可实时获取,因此BDS-2中与高度角相关的系统偏差可以借用载噪比信息进行加权修正。
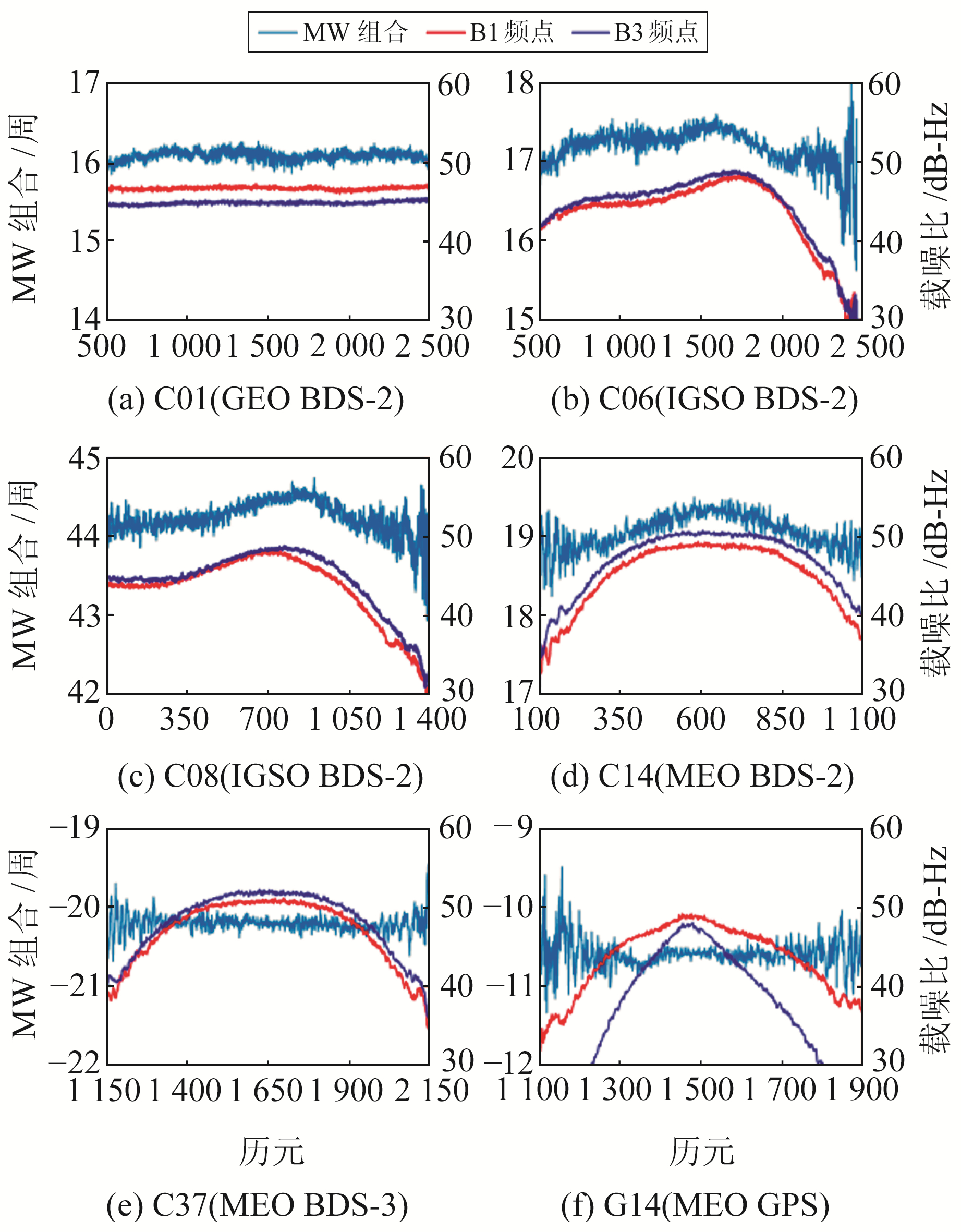
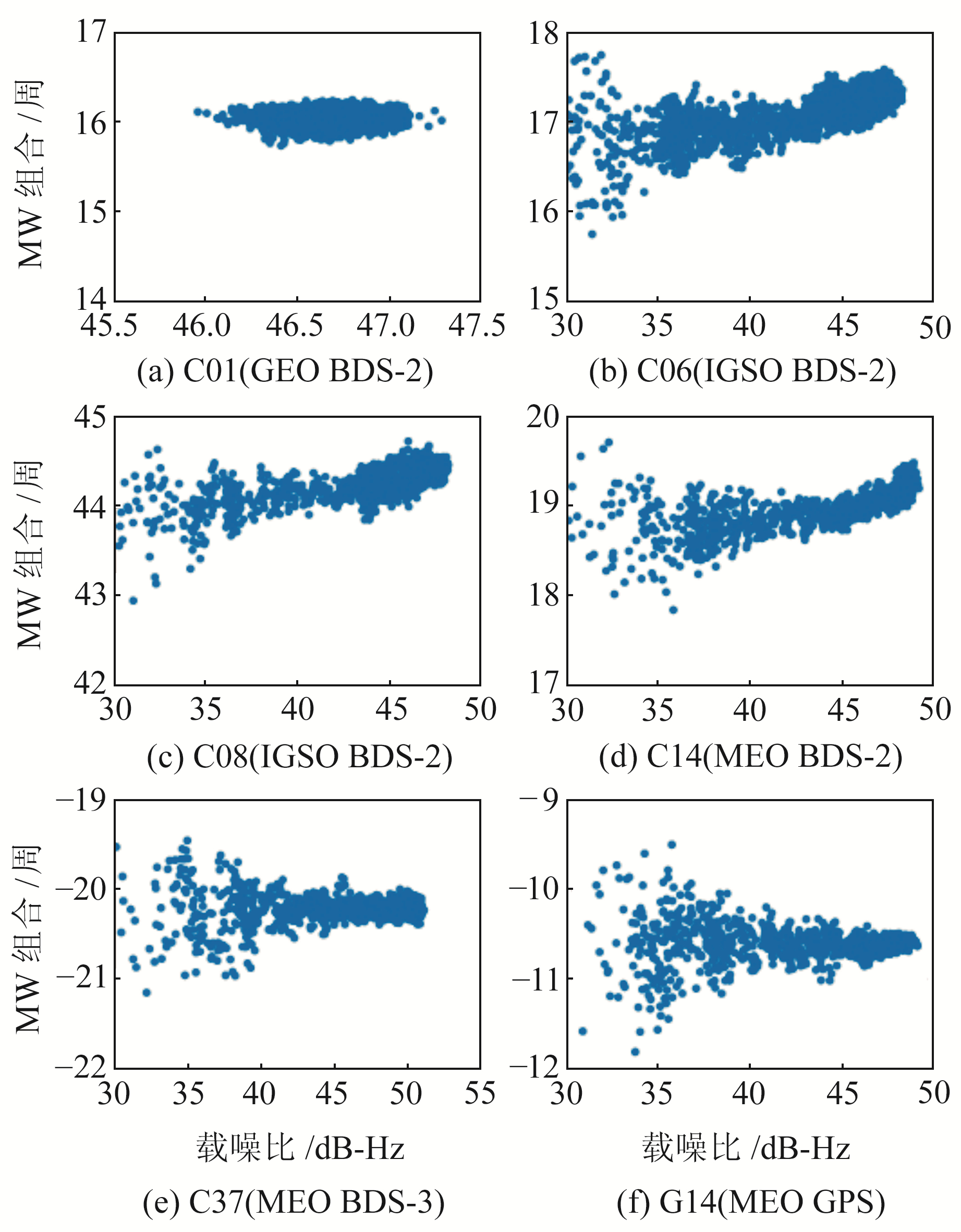
为验证基于载噪比加权的MW组合周跳探测方法的有效性,首先对BDS的MW组合观测值特性进行分析。本文利用CEDU测站2022-03-15的实测数据,采用BDS的B1和B3两个频点构建MW组合观测值进行分析,采样间隔为30 s。图 1、2分别为BDS和GPS部分卫星MW组合观测值(以周为单位)的时间序列和载噪比序列。
|
图 1 BDS和GPS的MW组合观测值时间序列 Fig. 1 The time series of BDS and GPS of MW combination observation |
|
图 2 BDS和GPS的MW组合观测值的载噪比序列 Fig. 2 The CNR series of BDS and GPS of MW combination observation |
从图 1可以看出,MW组合观测值的波动大小与观测信号的载噪比具有一定的相关性:载噪比较高时MW组合观测值波动较小,载噪比较低时MW组合观测值波动较大。由图 2可见,BDS-2的GEO卫星(图 2(a))、BDS-3卫星(图 2(e))、GPS卫星(图 2(f))的MW组合观测值围绕固定值波动,载噪比变化只对MW组合观测值的波动大小产生影响,MW组合观测值并未产生系统性偏差;BDS-2的IGSO卫星(图 2(b)、2(c))和MEO卫星(图 2(d))的MW组合观测值存在系统性偏差,MW组合观测值和载噪比呈现出基本一致的变化趋势,即载噪比较高的历元,其MW组合观测值也较大,反之亦然。
从图 2还可以看出,相比于BDS-2的GEO、BDS-3、GPS卫星,BDS-2的IGSO和MEO卫星的MW组合观测值存在明显的系统偏差,主要表现为IGSO和MEO卫星的MW组合观测值随载噪比的增大呈上升趋势,而其他卫星的MW组合观测值则围绕固定数值波动,不随载噪比变化。由此可知,若按照传统TurboEdit算法对BDS-2的IGSO和MEO卫星全部历元求平均,则会因为BDS-2存在系统偏差而影响MW组合中计算出的平均宽巷模糊度和均方根,从而影响周跳探测性能,造成周跳漏检或误检。
3 TurboEdit算法改进 3.1 基于载噪比加权的MW组合在BDS-2的IGSO、MEO卫星的载噪比和MW组合观测值相关性分析的基础上,基于传统TurboEdit算法,在计算历元i的平均宽巷模糊度NWL(i)时引入载噪比加权方法,替代前(i-1)个历元的算数平均值,其权重为历元i的载噪比与之前所有历元载噪比之差的指数倒数。计算历元i的平均宽巷模糊度均方根时,利用残差平方的加权平均值代替均方根,避免因均方根过大而引起周跳漏判。具体数学模型为:
| $ \bar{N}_{\mathrm{WL}}(i)=\frac{\sum\limits_{j=1}^i w(j) N_{\mathrm{WL}}(j)}{\sum\limits_{j=1}^i w(j)} $ | (13) |
| $ \sigma^2(i)=\frac{\sum\limits_{j=1}^i w(j)\left[N_{\mathrm{WL}}(j)-\bar{N}_{\mathrm{WL}}(i-1)\right]^2}{\sum\limits_{j=1}^i w(j)} $ | (14) |
式中,载噪比加权系数w(j)可表示为:
| $ w(j)=w_1(j)+w_2(j) $ | (15) |
其中,
| $ w_k(j)=\log \left(S_k(j)\right) \frac{1}{\exp \left(\left|S_k(i)-S_k(j)\right|\right)} $ | (16) |
式中,Sk为频点fk信号对应的载噪比。判断是否发生周跳的条件不变:若满足式(8),则认为历元i存在周跳。
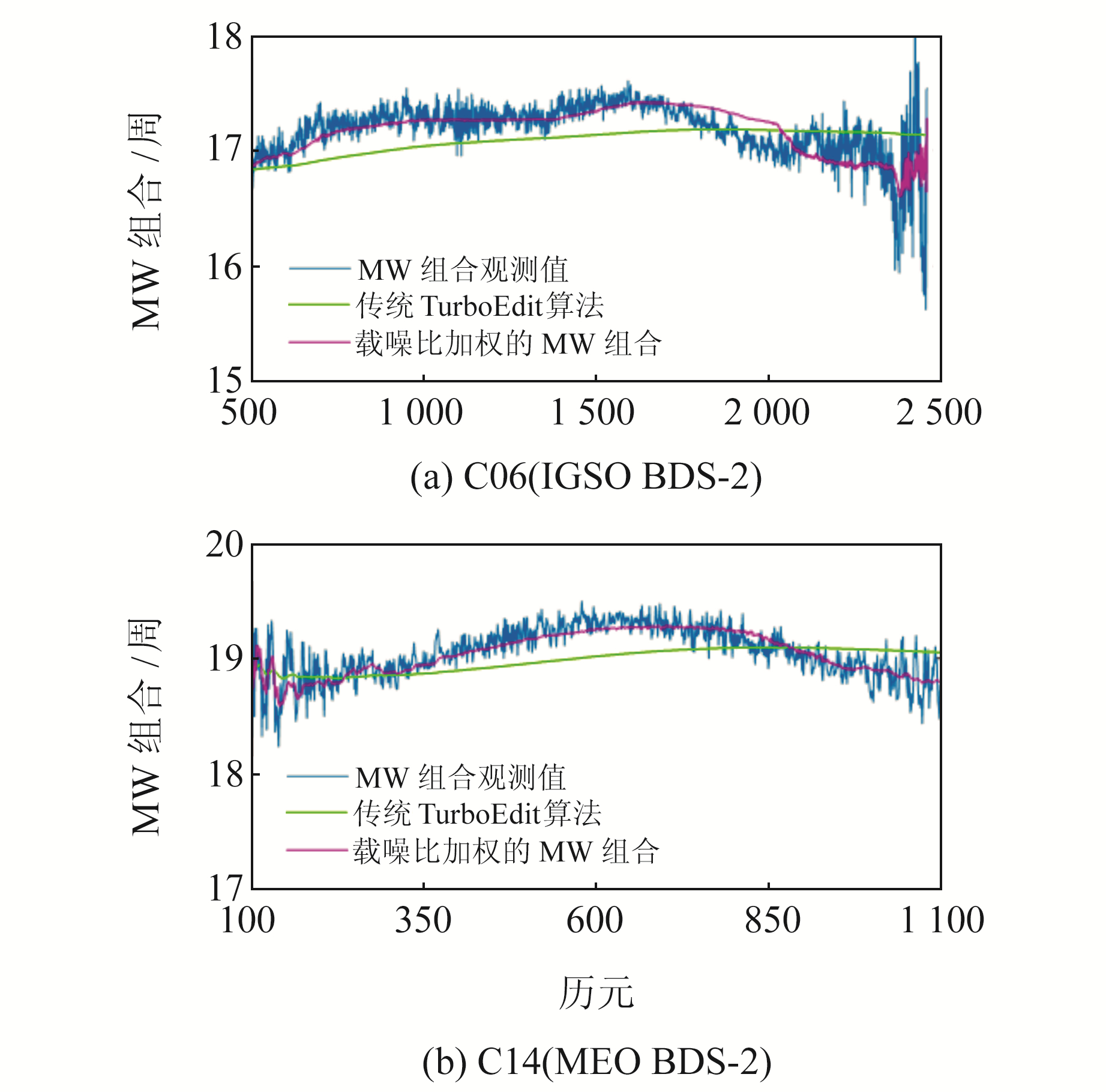
为了能够直观地展示载噪比加权的MW组合优越性,图 3分别给出C06卫星(IGSO BDS-2)和C14卫星(MEO BDS-2)的MW组合观测值、传统TurboEdit算法和载噪比加权的MW组合计算出的平均宽巷模糊度。由图 3可见,相比于传统TurboEdit算法,载噪比加权的MW组合计算出的平均宽巷模糊度具有更好的拟合效果,能够更好地反映MW组合观测值的真实变化情况。
|
图 3 MW组合变化 Fig. 3 The variation of MW combination |
直接利用载波相位观测值进行相邻历元求差,可以去除噪声较大的伪距观测量对探测结果的影响,从而有效提升探测精度。使用载波相位观测值进行一次历元间差分的GF组合数学模型为:
| $ \begin{array}{c} \Delta L_{\mathrm{GF}}(i)=L_{\mathrm{GF}}(i)-L_{\mathrm{GF}}(i-1)= \\ \lambda_1 \Delta N_1-\lambda_2 \Delta N_2+\mathit{\Delta} \nabla I \end{array} $ | (17) |
式中,
考虑到电离层有可能发生剧烈变化,为了更好地消除电离层延迟的趋势项影响,对GF组合进行二次历元间差分,其数学模型为:
| $ \nabla \Delta L_{\mathrm{GF}}(i)=\Delta L_{\mathrm{GF}}(i)-\Delta L_{\mathrm{GF}}(i-1) $ | (18) |
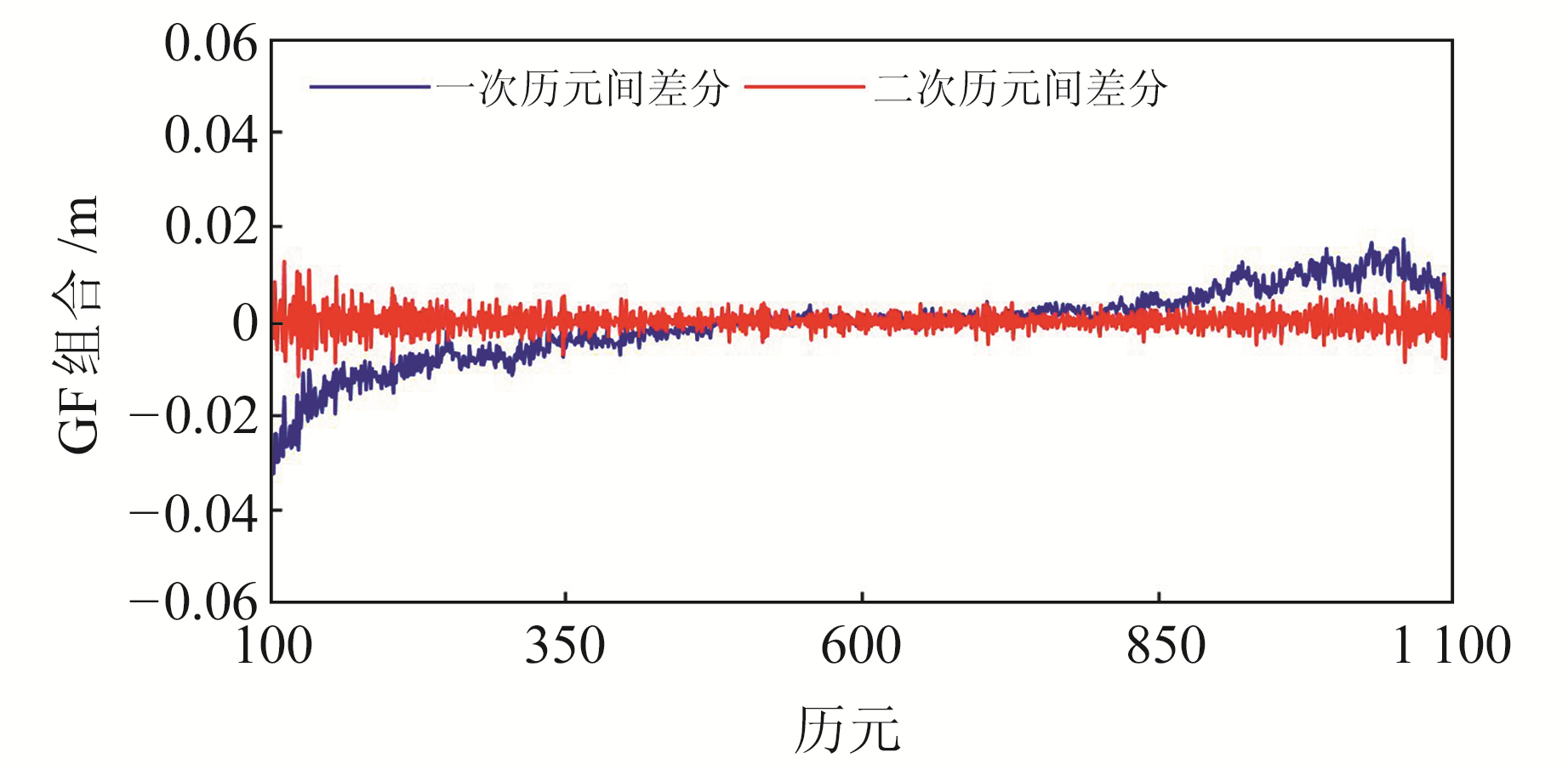
图 4为C14卫星(MEO BDS-2)一次历元间差分和二次历元间差分的GF组合变化曲线。从图中可以看出,一次历元间差分的电离层残差具有较为明显的变化,二次历元间差分的电离层残差较为平稳,变化趋势明显小于一次历元间差分。因此,当电离层活动剧烈或采样间隔较大时,二次历元差分探测周跳的效果更好。
|
图 4 GF组合变化 Fig. 4 The variation of GF combination |
基于载噪比加权的MW组合与基于二次历元间差分的GF组合均具有周跳探测的不敏感性,单一组合只能探测周跳发生的历元而无法准确判断周跳发生的频段和大小。结合2种组合可以克服单一组合存在的缺陷,可分离并修复周跳。二者联合的数学模型为:
| $ \left\{\begin{array}{l} \Delta N_{\mathrm{WL}}=\operatorname{round}\left(\Delta N_1-\Delta N_2\right) \\ \nabla \mathit{\Delta} L_{\mathrm{GF}}(i)=\lambda_1 \Delta N_1-\lambda_2 \mathit{\Delta} N_2 \end{array}\right. $ | (19) |
为方便周跳探测,在传统TurboEdit算法中构建检验量D。D可表示为宽巷模糊度的变化量与均方根的比值:
| $ D=\frac{\left|N_{\mathrm{WL}}(i)-\bar{N}_{\mathrm{WL}}(i-1)\right|}{\sigma(i-1)} $ | (20) |
当|D|>k时,认为历元i存在周跳,探测阈值k通常设置为4。
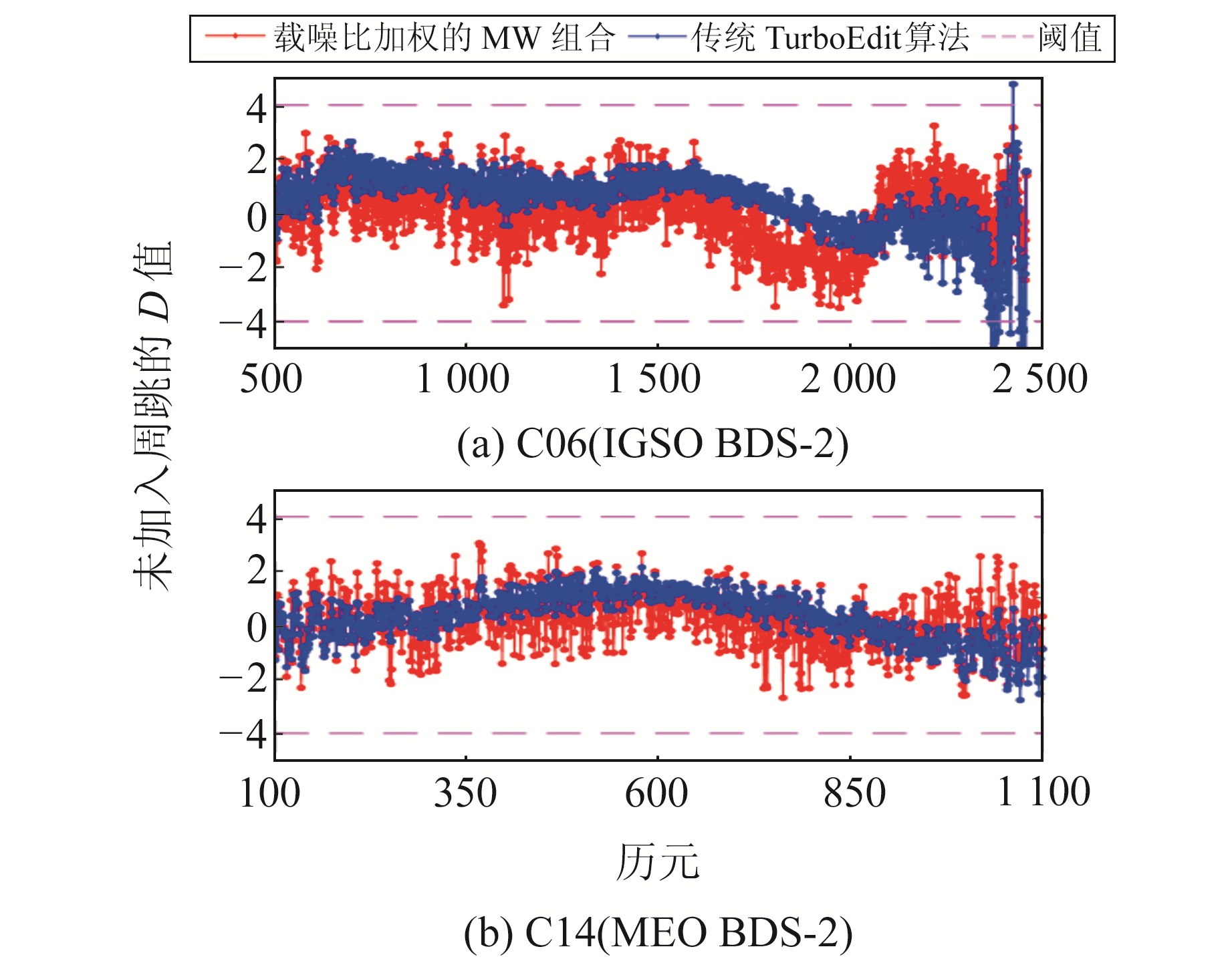
4.1 无周跳情况选取C06卫星(IGSO BDS-2)和C14卫星(MEO BDS-2)进行分析。根据§3.2中二次历元间差分的GF组合验证可知,原始数据无周跳。图 5为传统TurboEdit算法和载噪比加权MW组合的D值变化曲线。
|
图 5 D值变化曲线(无周跳) Fig. 5 The variation of D value(no cycle slip) |
由图 5可见,载噪比加权的MW组合D值围绕固定值0波动,相比于传统TurboEdit算法,该算法在一定程度上消除了系统偏差。从图 5(a)可以看出,TurboEdit算法部分历元的D值超出阈值,此时发生周跳误检,误检的历元数约为15个,而载噪比加权的MW组合不存在周跳误检。
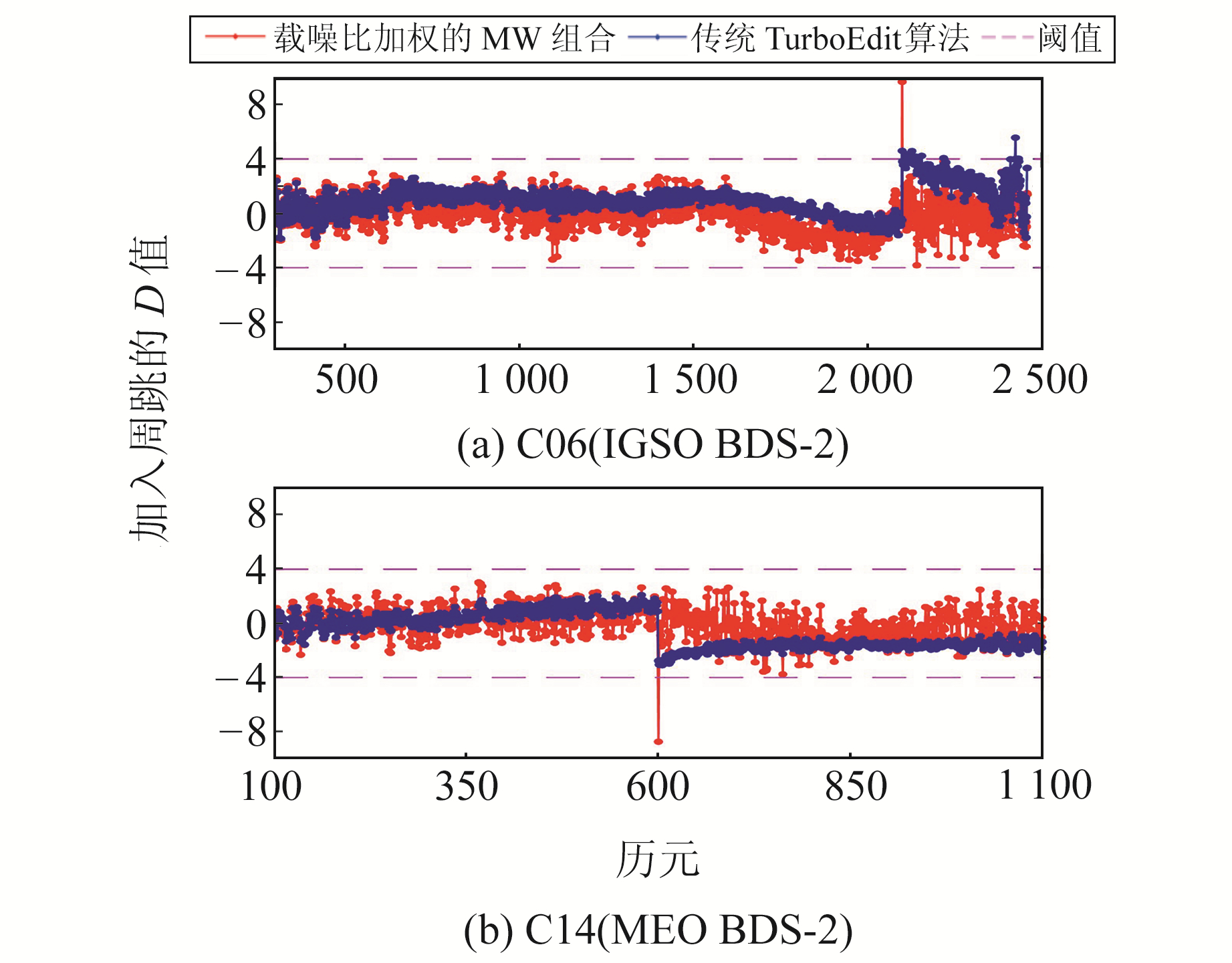
4.2 有周跳情况为验证载噪比加权的MW组合算法的有效性,在无周跳的原始数据上模拟周跳进行探测实验。图 6为实测BDS数据中加入模拟周跳的实验结果。
|
图 6 D值变化曲线(有周跳) Fig. 6 The variation of D value(with cycle slip) |
从图 6(a)可以看出,在C06卫星(IGSO BDS-2) B1频点2 100历元处加入大小为1周的周跳后,传统TurboEdit算法的D值超出阈值,此时周跳探测成功,但随后历元的D值仍然超出阈值,发生周跳误检;载噪比加权的MW组合成功探测出模拟加入的周跳,且后续历元未发生周跳误检。由此可知,载噪比加权的MW组合可以减少传统TurboEdit算法在BDS-2中因系统偏差而造成的周跳误检。
从图 6(b)可以看出,在C14卫星(MEO BDS-2) B3频点600历元处加入大小为1周的周跳后,传统TurboEdit算法的D值未超出阈值,此时发生周跳漏检;载噪比加权的MW组合成功探测出加入的模拟周跳。由此可知,载噪比加权的MW组合可以减少传统TurboEdit算法在BDS-2部分卫星中因系统偏差而造成的周跳漏检。
综上所述,BDS-2非GEO卫星存在的系统偏差使得传统TurboEdit算法的MW组合探测周跳时出现漏检或误检现象,载噪比加权的MW组合可有效解决上述问题。
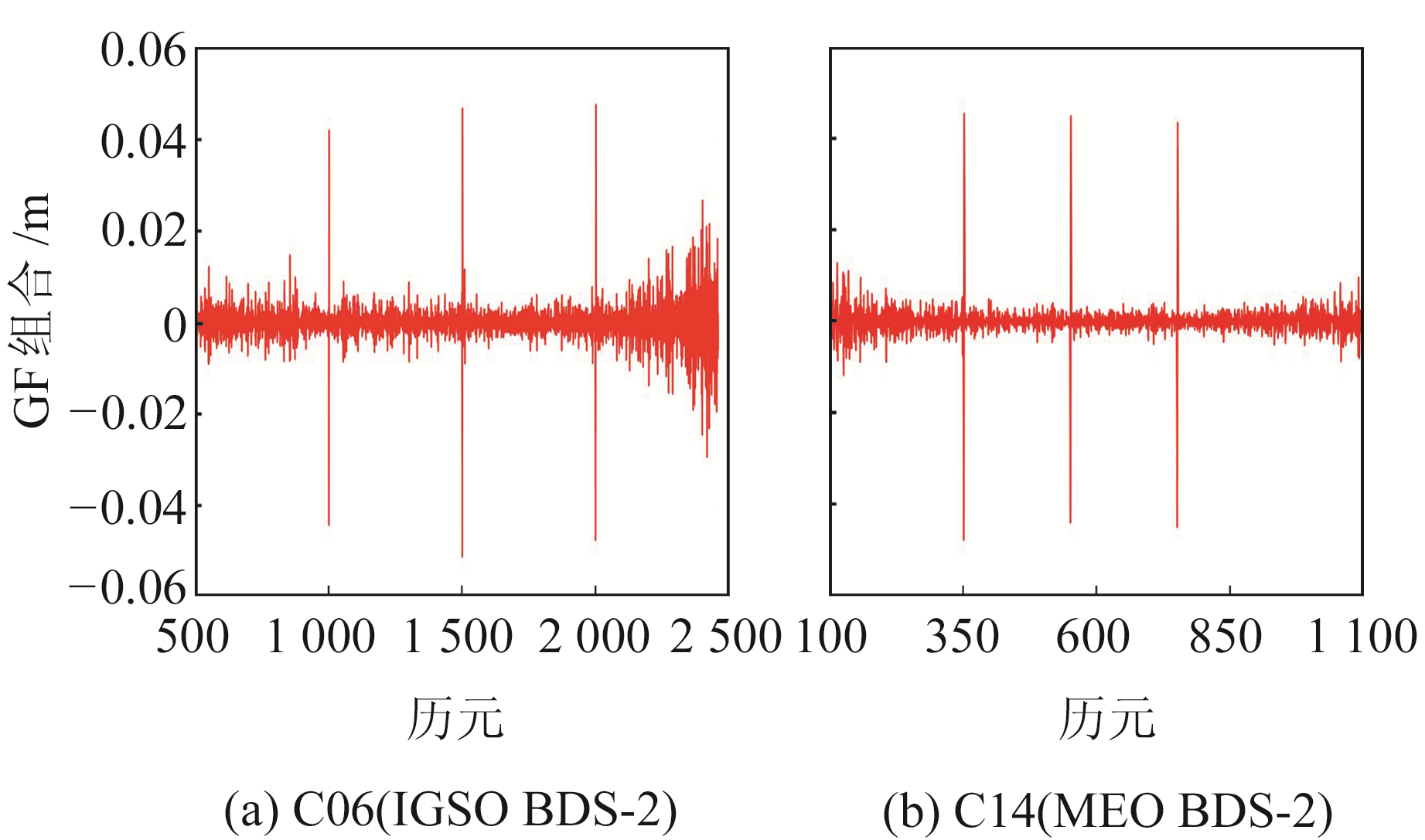
4.3 等值周跳在C06卫星1 000、1 500、2 000历元和C14卫星350、550、750历元B1、B3频点处加入(1, 1)的等值周跳组合后,载噪比加权的MW组合周跳探测失败。结果表明,载噪比加权的MW组合在同一历元的2个频点发生等值周跳时无法进行探测,因此可选取GF组合继续进行周跳探测。由于电离层可能发生剧烈变化,因此本文采取二次历元间差分的GF组合进行探测,结果如图 7所示。
|
图 7 二次历元间差分的GF组合(等值周跳) Fig. 7 Second-order time-difference of GF combination (equal cycle slip) |
从图 7可以看出,二次历元间差分的GF组合可以成功探测出等值周跳。由此可知,联合载噪比加权的MW组合和二次历元间差分的GF组合可以克服单个组合存在的不敏感周跳问题,能够有效探测周跳。
4.4 联合周跳探测修复为继续验证载噪比加权的MW组合算法的有效性,进一步加入周跳进行探测实验。模拟加入的小周跳组合及实验结果见表 1。
|
|
表 1 周跳探测与修复结果 Tab. 1 Results of cycle slip detection and repairing |
从表 1可以看出,联合载噪比加权的MW组合和二次历元间差分的GF组合可相互补充单个组合的不足,从而探测出所有组合的周跳。
5 结语本文提出一种载噪比加权的MW组合模型,相比于传统TurboEdit算法,该模型计算的平均宽巷模糊度具有更好的拟合效果,可以更有效地反映MW组合观测值的真实变化情况,有效减少因BDS-2中IGSO和MEO卫星的MW组合观测值存在系统偏差而造成的周跳漏检和误检,提升周跳探测性能。在此基础上,进一步联合二次历元间差分的GF组合,可以准确探测出所有周跳组合。
| [1] |
Blewitt G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3): 199-202 DOI:10.1029/GL017i003p00199
(  0) 0) |
| [2] |
张小红, 曾琪, 何俊, 等. 构建阈值模型改善TurboEdit实时周跳探测[J]. 武汉大学学报: 信息科学版, 2017, 42(3): 285-292 (Zhang Xiaohong, Zeng Qi, He Jun, et al. Improving TurboEdit Real-Time Cycle Slip Detection by the Construction of Threshold Model[J]. Geomatics and Information Science of Wuhan University, 2017, 42(3): 285-292)
(  0) 0) |
| [3] |
王振杰, 聂志喜, 欧吉坤. 一种基于TurboEdit改进的GPS双频观测值周跳探测方法[J]. 武汉大学学报: 信息科学版, 2014, 39(9): 1 017-1 021 (Wang Zhenjie, Nie Zhixi, Ou Jikun. An Improved Cycle Slip Detection Based on Turbo Edit Method for Dual-Frequency GPS Receiver[J]. Geomatics and Information Science of Wuhan University, 2014, 39(9): 1 017-1 021)
(  0) 0) |
| [4] |
范丽红, 王利, 张明, 等. 基于MW与STPIR组合的周跳探测与修复方法研究[J]. 武汉大学学报: 信息科学版, 2015, 40(6): 790-794 (Fan Lihong, Wang Li, Zhang Ming, et al. A Combination of MW and Second-Order Time-Difference Phase Ionospheric Residual for Cycle Slip Detection and Repair[J]. Geomatics and Information Science of Wuhan University, 2015, 40(6): 790-794)
(  0) 0) |
| [5] |
党子越, 夏凤雨. 一种基于改进TurboEdit的GPS周跳探测与修复方法[J]. 大地测量与地球动力学, 2016, 36(8): 723-726 (Dang Ziyue, Xia Fengyu. An Improved Detection and Repair Method for Cycle Slips Based on TurboEdit Algorithm[J]. Journal of Geodesy and Geodynamics, 2016, 36(8): 723-726)
(  0) 0) |
| [6] |
杨阳阳, 刘宁, 张永志. 一种基于双频非差GNSS相位数据的周跳实时探测与修复方法[J]. 大地测量与地球动力学, 2017, 37(11): 1 173-1 177 (Yang Yangyang, Liu Ning, Zhang Yongzhi. A New Algorithm of Cycle Slip Real-Time Detection and Repair Based on Un-Differenced Dual-Frequency GNSS Carrier Phase Data[J]. Journal of Geodesy and Geodynamics, 2017, 37(11): 1 173-1 177)
(  0) 0) |
| [7] |
冯绪, 刘长建, 鲍亚东, 等. 基于BIC准则的双向TurboEdit算法[C]. 第九届中国卫星导航学术年会, 哈尔滨, 2018 (Feng Xu, Liu Changjian, Bao Yadong, et al. The Bidirection TurboEdit Algorithm Based on BIC[C]. The 9th China Satellite Navigation Conference, Harbin, 2018)
(  0) 0) |
| [8] |
Qu C, Ye X Z, Liu W X, et al. Detection and Repair of Cycle Slips with BDS Dual Frequency Combination[C]. 2017 IEEE 3rd Information Technology and Mechatronics Engineering Conference(ITOEC), Chongqing, 2017
(  0) 0) |
| [9] |
张晨晰, 党亚民, 薛树强, 等. 一种基于TurboEdit的BDS周跳探测改进方法[J]. 测绘科学, 2021, 46(6): 47-52 (Zhang Chenxi, Dang Yamin, Xue Shuqiang, et al. An Improved BDS Cycle Slip Detection Method Based on TurboEdit[J]. Science of Surveying and Mapping, 2021, 46(6): 47-52)
(  0) 0) |
| [10] |
Wanninger L, Beer S. Beidou Satellite-Induced Code Pseudorange Variations: Diagnosis and Therapy[J]. GPS Solutions, 2015, 19(4): 639-648 DOI:10.1007/s10291-014-0423-3
(  0) 0) |
| [11] |
王广兴. 北斗观测值特性分析及其在PPP模糊度固定应用中的研究[D]. 武汉: 武汉大学, 2016 (Wang Guangxing. Characteristics Analysis of Beidou Observations and Its Application in PPP Ambiguity Fixation[D]. Wuhan: Wuhan University, 2016)
(  0) 0) |
| [12] |
蔡成林, 王亮亮, 刘昌盛, 等. 利用改进型TurboEdit算法进行BDS载波相位周跳检测与修复[J]. 武汉大学学报: 信息科学版, 2016, 41(12): 1 632-1 637 (Cai Chenglin, Wang Liangliang, Liu Changsheng, et al. The Cycle-Slip Detection and Repair of BDS Based on Improved TurboEdit Algorithm[J]. Geomatics and Information Science of Wuhan University, 2016, 41(12): 1 632-1 637)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43

