目前,GNSS芯片几乎搭载在每个智能手机、平板电脑等移动终端上。2016-05谷歌在开发者大会上宣布,Android Nougat操作系统中的应用程序将可以使用原始GNSS测量值,引发学者讨论[1]。Hatch[2]于1983年首次提出可以提高伪距精度的载波相位平滑伪距方法,但当载波相位观测值发生周跳时,精度将受到较大影响[3-4]。由于多普勒观测值不受多路径误差的干扰且较为稳定,具有较好的观测精度[5],因此采用多普勒观测值平滑伪距法可以提高定位精度和稳定性,效果优于单独的伪距单点定位法[6]。
速度是衡量载体运动的重要参数,将速度作为滤波预测模型的增量,辅助伪距观测量进行解算,可以达到平滑去噪的目的[7]。利用全球定位系统GPS进行速度测定的方法主要有3种:伪距差分法(PDVE)、历元间载波相位差分测速法(TDCPVE)[8]和多普勒测速法(DVE)[9]。上述3种方法单独使用时都存在缺点,联合使用则可以优势互补。
本文首先介绍多普勒测速模型和一种改进的历元间载波相位差分测速模型;然后介绍基于星间差的载波相位平滑伪距、星间差多普勒平滑伪距和星间差位置变化约束的自适应滤波切换算法,并采用三阈值作抗差处理,针对双频或多频提出一种不受电离层发散效应影响的相位平滑算法;最后分别在静态和动态环境下进行实验,将星间差载波平滑伪距、星间差多普勒平滑伪距和星间差位置变化约束的自适应滤波切换算法与普通抗差伪距法进行精度对比。
1 测速模型 1.1 多普勒测速由于接收机和卫星的相对运动会导致信号在接收端的频率发生频移,即接收的信号频率与发射的信号频率不一致,这种频率的偏移量称为多普勒频移。具体公式为:
| $ f_{\mathrm{d}}=f_{\mathrm{m}}-f=-\frac{1}{c} \frac{\mathrm{d} \rho}{\mathrm{d} t} f $ | (1) |
式中,c为光速;ρ为卫地距;
由于多普勒观测值会受到卫星钟速、接收机钟速、对流层和电离层延迟变化等的影响,因此多普勒观测方程为:
| $\begin{array}{c} D_{\mathrm{m}}^{\mathrm{s}}=\dot{\rho}_{\mathrm{m}}^{\mathrm{s}}+\dot{\delta t}_{\mathrm{m}}-\dot{\delta t^{\mathrm{s}}}+\delta \dot{\operatorname{Trop}}_{\mathrm{m}}^{\mathrm{s}}-\\ \delta \dot{\operatorname{Ion}}_{\mathrm{m}}^{\mathrm{s}}+\varepsilon_{D_{\mathrm{m}}}^{\mathrm{s}} \end{array} $ | (2) |
将卫地距变化率
| $\begin{array}{c} D_{\mathrm{m}}^{\mathrm{s}}=\mathrm{e} \dot{\boldsymbol{r}}^{\mathrm{s}}-\mathrm{e} \dot{\boldsymbol{r}}_{\mathrm{m}}+\dot{\delta t}_{\mathrm{m}}-\dot{\delta t^{\mathrm{s}}}+\\ \delta \dot{\operatorname{Trop}}_{\mathrm{m}}^{\mathrm{s}}-\delta \dot{\operatorname{Ion}}_{\mathrm{m}}^{\mathrm{s}}+\varepsilon_{D_{\mathrm{m}}}^{\mathrm{s}} \end{array} $ | (3) |
式中,[·]为对时间的导数,上标s为卫星号,下标m为接收机号,Dms为多普勒观测值,
载波相位历元差分测速是指将同一卫星的载波相位定位观测方程在相邻历元间进行差分,通过卫星和接收机之间精确的几何位置关系估计接收机坐标在相邻历元间的变化量,通过速度和位移的关系求解运动载体的平均速度。其观测方程为:
| $ \begin{array}{l} \Delta \varPhi_{\mathrm{m} t_{n, n-1}}^{\mathrm{s}}=\Delta \rho_{\mathrm{m} t_{n, n-1}}^{\mathrm{s}}+\Delta \delta t_{\mathrm{m} t_{n, n-1}}-\Delta \delta t_{t_{n, n-1}}^{\mathrm{s}}+ \\ \quad \Delta \delta \operatorname{Trop}_{\mathrm{mt}_{n, n-1}}^{\mathrm{s}}-\Delta \delta \operatorname{Ion}_{\mathrm{m} t_{n, n-1}}^{\mathrm{s}}+\Delta \varepsilon_{\varPhi_{\mathrm{m}t_{n, n}, 1}}^{\mathrm{s}} \end{array} $ | (4) |
式中,Δ为单差算子,ΔΦsmtn, n-1为第n个历元和第(n-1)个历元的载波相位观测值之差,Δρsmtn, n-1为历元间卫地距变化,Δδtmtn, n-1和Δδtstn, n-1分别为历元间单差接收机钟差和历元间单差卫星钟差,ΔδTropsmtn, n-1和ΔδIonsmtn, n-1分别为历元间对流层单差和历元间电离层单差,ΔεsΦmtn, n-1为历元间载波相位噪声单差。若不发生周跳,则整周模糊度会自动消除。智能手机的采样间隔较小,很多误差具有较强的相关性,历元差分后的方程可以用式(5)代替:
| $ \begin{array}{c} \Delta \varPhi_{\mathrm{m} t_{n, n-1}}^{\mathrm{s}}=\Delta \rho_{\mathrm{m} t_{n, n-1}}^{\mathrm{s}}+\Delta \delta t_{\mathrm{m} t_{n, n-1}}- \\ \Delta \delta t_{t_{n, n-1}}^{\mathrm{s}}+\Delta \varepsilon_{\varPhi_{\mathrm{m} t_{n, n-1}}}^{\mathrm{s}} \end{array} $ | (5) |
式中,卫星到接收机的几何距离可以表示为:
| $ \rho_{\mathrm{m} t_i}^{\mathrm{s}}=\left(\boldsymbol{e}_{t_i}, \left(R_{\mathrm{m} t_i}^{\mathrm{s}}-r_{t_i}\right)\right) $ | (6) |
通过式(6)可得:
| $ \begin{array}{c} \Delta \rho_{\mathrm{m} t_{n, n-1}}^{\mathrm{s}}=\Delta \rho_{\mathrm{m} t_n}^{\mathrm{s}}-\Delta \rho_{\mathrm{m} t_{n-1}}^{\mathrm{s}}= \\ \left(\boldsymbol{e}_{t_n}, \left(R_{\mathrm{m} t_n}^{\mathrm{s}}-r_{t_n}\right)\right)-\left(\boldsymbol{e}_{t_{n-1}}, \left(R_{\mathrm{m} t_{n-1}}^{\mathrm{s}}-r_{t_{n-1}}\right)\right)= \\ \left(\boldsymbol{e}_{t_n}, R_{\mathrm{m} t_n}^{\mathrm{s}}\right)-\left(\boldsymbol{e}_{t_n}, r_{t_n}\right)-\left(\boldsymbol{e}_{t_{n-1}}, R_{\mathrm{m} t_n}^{\mathrm{s}}\right)+\left(\boldsymbol{e}_{t_{n-1}}, r_{t_{n-1}}\right) \end{array} $ | (7) |
式中,
| $ \begin{array}{c} \Delta \rho_{\mathrm{m} t_{n, n-1}}^{\mathrm{s}}=-\left(\boldsymbol{e}_{t_n}, \Delta r\right)+\left(\boldsymbol{e}_{t_n}, R_{\mathrm{m} t_n}^{\mathrm{s}}\right)-\\ \left(\boldsymbol{e}_{t_{n-1}-1}, R_{\mathrm{m} t_{n-1}}^{\mathrm{s}}\right)-\left(\boldsymbol{e}_{t_n}, r_{t_{n-1}}\right)+\left(\boldsymbol{e}_{t_{n-1}}, r_{t_n}\right)= \\ -\left(\boldsymbol{e}_{t_n}, \Delta r\right)+\left(\boldsymbol{e}_{t_n}, R_{\mathrm{m} t_n}^{\mathrm{s}}-r_{t_{n-1}}\right)- \\ \left(\boldsymbol{e}_{n-1}, R_{\mathrm{m} t_{n-1}}^{\mathrm{s}}-r_{t_{n-1}}\right) \end{array} $ | (8) |
将式(8)代入式(5),求出位置变化量Δr,根据
历元间载波相位差分测速的精度较高,对载波相位观测值的要求也较高。在恶劣的观测环境下,若频繁发生周跳,则可以将位置差分测速、历元间载波相位差分测速和多普勒测速模型相结合,提高历元间载波相位差分测速的稳定性。观测方程为[10]:
| $ \left\{\begin{array}{l} \Delta \varPhi_{\mathrm{m} t_{n, n-1}}^{\mathrm{s}}=-\left(\boldsymbol{e}_{t_n}, \Delta r\right)+\Delta \delta t_{\mathrm{m} t_{n, n-1}}-\Delta \delta t_{t_{n, n-1}}^{\mathrm{s}}+ \\ \;\;\;\left(\boldsymbol{e}_{t_n}, R_{\mathrm{m} t_n}^{\mathrm{s}}-r_{n-1}\right)-\left(\boldsymbol{e}_{t_{n-1}}, R_{\mathrm{m} t_{n-1}}^{\mathrm{s}}-r_{n-1}\right) \\ \Delta P_{\mathrm{m} t_{n, n-1}}^{\mathrm{s}}=-\left(\boldsymbol{e}_{t_n}, \Delta r\right)+\Delta \delta t_{\mathrm{m} t_{n, n-1}}-\Delta \delta t_{t_{n, n-1}}^{\mathrm{s}}+ \\ \;\;\;\left(\boldsymbol{e}_{t_n}, R_{\mathrm{m} t_n}^{\mathrm{s}}-r_{n-1}\right)-\left(\boldsymbol{e}_{t_{n-1}}, R_{\mathrm{m} t_{n-1}}^{\mathrm{s}}-r_{n-1}\right) \\ D=-\left(\boldsymbol{e}_{t_n}, \dot{r}_{t_n}\right)+\dot{\delta t}_{\mathrm{m}}-\dot{\delta t}_{t_n}^{\mathrm{s}}+\left(\boldsymbol{e}_{t_n}, \dot{R}_{\mathrm{m} t_n}^{\mathrm{s}}\right) \end{array}\right. $ | (9) |
式(9)可通过最小二乘法进行参数估计,当采样间隔为1 s时,v=Δr,未知参数为x、y、z方向上的速度。
2 伪距平滑由于智能手机受天线及内部硬件影响,在观测环境较差时,定位解算结果会受到严重影响。智能手机的伪距精度同样处于低水平状态,其伪距误差可达数m,正常的伪距解算结果偏差也较大,在导航定位时起到的作用较为有限。本文将伪距单点定位加入抗差中并设定阈值,将大于阈值的最大验后残差剔除。虽然抗差可以提升精度,但伪距观测值噪声较大,且载波相位和多普勒在智能手机中的精度远高于伪距精度,因此可使用载波相位和多普勒平滑伪距来削弱伪距观测值中的噪声[11-12]。
2.1 基于星间差的载波平滑伪距载波平滑伪距可以在很大程度上降低伪距噪声。Hatch滤波器是一种递归滤波器,利用当前历元的观测值和之前历元平滑所得载波平滑伪距的估计值,得到当前历元的载波平滑伪距值,可以在低成本GNSS接收机中实现实时操作。Hatch滤波器的方程式为:
| $ \left\{\begin{array}{l} \bar{P}_{\mathrm{m} t_n}^{\mathrm{s}}=P_{\mathrm{m} t_1}^{\mathrm{s}}, n=1 \\ \bar{P}_{\mathrm{m} t_n}^{\mathrm{s}}=\frac{1}{n} P_{\mathrm{m} t_n}^{\mathrm{s}}+\frac{n-1}{n} \cdot \\ \quad\left(\bar{P}_{\mathrm{m} t_{n-1}}^{\mathrm{s}}+\varPhi_{\mathrm{m} t_n}^{\mathrm{s}}-\varPhi_{\mathrm{m} t_{n-1}}^{\mathrm{s}}\right), n \neq 1 \end{array}\right. $ | (10) |
式中,
为避免Android设备载波相位观测中不同的接收机时钟偏差与伪距时钟偏差带来的影响,本文对卫星间观测值作差。根据Hatch滤波平滑算法,利用卫星间单差建立载波平滑伪距观测值[13]:
| $ \left\{\begin{array}{l} \bar{P}_{\mathrm{m} t_n}^{\mathrm{s}, \mathrm{r}}=\frac{1}{n} P_{\mathrm{m} t_n}^{\mathrm{s}, \mathrm{r}}+ \\ \;\;\;\;\frac{n-1}{n}\left(\bar{P}_{\mathrm{m} t_{n-1}}^{\mathrm{s}, \mathrm{r}}+\varPhi_{\mathrm{m} t_n}^{\mathrm{s}, \mathrm{r}}-\varPhi_{\mathrm{m} t_{n-1}}^{\mathrm{s}, \mathrm{r}}\right) \\ P_{\mathrm{m} t_n}^{\mathrm{s}, \mathrm{r}}=P_{\mathrm{m} t_n}^{\mathrm{s}}-P_{\mathrm{m} t_n}^{\mathrm{r}} \\ \varPhi_{\mathrm{m} t_n}^{\mathrm{s}, \mathrm{r}}=\varPhi_{\mathrm{m} t_n}^{\mathrm{s}}-\varPhi_{\mathrm{m} t_n}^{\mathrm{r}} \\ \bar{P}_{\mathrm{m} t_1}^{\mathrm{s}, \mathrm{r}}=P_{\mathrm{m} t_1}^{\mathrm{s}, \mathrm{r}} \end{array}\right. $ | (11) |
式中,
1) 根据历元间三差法确定载波相位的周跳与粗差。
2) 利用伪距速率和相位速率之间的差异来检测粗差。在无粗差的情况下,
| $ \left|\left(P_{\mathrm{m} t_n}^{\mathrm{s}}-P_{\mathrm{m} t_{n-1}}^{\mathrm{s}}\right)-\left(\varPhi_{\mathrm{m} t_n}^{\mathrm{s}}-\varPhi_{\mathrm{m} t_{n-1}}^{\mathrm{s}}\right)\right|<\xi_1 $ | (12) |
式中,ξ1为检测阈值[11],
3) 由于电离层历元间存在误差累积的现象,因此需要判定误差是否超出阈值,是否需要重置窗口进行平滑处理,检验公式为:
| $ \left|\bar{P}_{\mathrm{m} t_n}^{\mathrm{s}}-P_{\mathrm{m} t_{n-1}}^{\mathrm{s}}\right|<\xi_2 $ | (13) |
式中,ξ2与ξ1含义相同。
若相位与伪距的电离层放大因子不相等,则会出现电离层发散效应。有一种不受电离层发散效应影响的相位平滑算法,但该方法只适用于含有双频或多频的观测数据。本文所述2款移动智能终端的双频段为L1与L5,其伪距平滑计算公式分别为:
| $ \begin{array}{c} \bar{P}_{{1 t_n}}^{\mathrm{s}}=\frac{1}{n} P_{{1 t_n}}^{\mathrm{s}}+\frac{n-1}{n}\left(\bar{P}_{\mathrm{1}t_{n-1}}^{\mathrm{s}}+\Delta \varPhi_1^{\mathrm{s}}-\frac{2}{\mu-1} \cdot\right. \\ \left.\left(\mathrm{d} \varPhi_{t_n}^{\mathrm{s}}-\mathrm{d} \varPhi_{t_{n-1}}^{\mathrm{s}}\right)\right) \end{array} $ | (14) |
| $\begin{array}{c} \bar{P}_{5 t_n}^{\mathrm{s}}=\frac{1}{n} P_{1 t_n}^{\mathrm{s}}+\frac{n-1}{n}\left(\bar{P}_{5 t_{n-1}}^{\mathrm{s}}+\Delta \varPhi_5^{\mathrm{s}}-\frac{2 \mu}{\mu-1} \cdot\right.\\ \left.\left(\mathrm{d} \varPhi_{t_n}^{\mathrm{s}}-\mathrm{d} \varPhi_{t_{n-1}}^{\mathrm{s}}\right)\right) \end{array} $ | (15) |
其中,
| $ \begin{array}{l} \Delta \varPhi_1^{\mathrm{s}}=\varPhi_{1 t_n}^{\mathrm{s}}-\varPhi_{1 t_{n-1}}^{\mathrm{s}} \\ \mathrm{d} \varPhi_{t_n}^{\mathrm{s}}=\mathrm{d} \varPhi_{5 t_n}^{\mathrm{s}}-\mathrm{d} \varPhi_{1 t_n}^{\mathrm{s}} \end{array} $ | (16) |
式中,下标1为L1频段,下标5为L5频段,μ=f12/f52。式中组合相位观测值的电离层放大因子为1,与伪距观测值的放大因子相同,因此不会出现电离层放大效应。对含有双频数据的卫星,可采用式(15)进行平滑处理,其检核方式与单频载波相位平滑的检核方式相同。由于小米8与华为P40接收的部分卫星不含双频数据,因此将常规窗口单频平滑与双频无发散算法相结合进行平滑解算,同时采用抗差伪距的方式对平滑后的伪距进行解算。
2.2 基于星间差的多普勒平滑伪距多普勒平滑伪距方程为:
| $ \begin{array}{c} \bar{P}_{\mathrm{m} t_n}^{\mathrm{s}}= \\ \left.\frac{1}{n} P_{\mathrm{m} t_n}^{\mathrm{s}}+\frac{n-1}{n}\left(\bar{P}_{\mathrm{m} t_{n-1}}^{\mathrm{s}}+d_{\Delta D\left(t_n, t_{n-1}\right)}\right)\right) \end{array} $ | (17) |
在高频采样间隔下,多普勒观测值可以看作是载波相位观测值对时间的导数,因此式(17)中的dΔD(tn, tn-1)可表示为:
| $ \begin{array}{c} d_{\Delta D\left(t_n, t_{n-1}\right)}=\int_{t-\Delta t}^t D \mathrm{~d} \tau \approx \\ \frac{1}{2} \Delta t\left(D_n+D_{n-1}\right) \approx \lambda\left(\varPhi_n-\varPhi_{n-1}\right) \end{array} $ | (18) |
式中,Δt为2个相邻历元间的采样间隔。由式(18)可知,多普勒平滑伪距与载波相位平滑伪距相似,对式(17)进行星间差处理,可消去接收机钟差:
| $ \begin{array}{c} \bar{P}_{\mathrm{m} t_n}^{\mathrm{s}, \mathrm{r}}= \\ \frac{1}{n} P_{\mathrm{m} t_n}^{\mathrm{s}, \mathrm{r}}+\frac{n-1}{n}\left(\bar{P}_{\mathrm{m} t_{n-1}}^{\mathrm{s}, \mathrm{r}}+d_{\Delta D\left(t_n, t_{n-1}\right.}^{\mathrm{s}, \mathrm{r}}\right) \end{array} $ | (19) |
在使用多普勒平滑公式前同样需要按照§2.1中所述的三差法进行质量检核,若超出阈值则需要重置平滑窗口。
2.3 基于星间差位置变化约束的自适应滤波切换算法受硬件条件限制,智能手机伪距受多路径影响较大,载波相位或多普勒平滑至相对稳定状态所需时间较长。在动态导航定位中,载波与多普勒容易受外界环境干扰,粗差较多,导致窗口重置频繁,平滑结果受到影响。为充分利用载波与多普勒的高精度速度值,本文将其纳入到预测模型中,以此描述物体的运动变化情况,辅助伪距观测量进行解算,以达到平滑去噪的目的。
智能手机中多普勒的绝对精度存在差异,如华为P40的多普勒观测精度相对较差,构建准确的运动模型较为困难。当载体有较多速度与加速度变化时(如转弯),常规的常速度模型与常加速度模型会出现一定的偏差。同时,以伪距观测量为主体的量测方程本身精度较差,会出现整体性偏移。而载波历元差分测速的求解值为前后2个历元的位移变化,能更准确地表达载体位置移动情况,因此不将其转换为平均速度,而是直接作为位置估值的增量进行预测。若改进后的历元间载波相位差分测速不能进行正确求解,则采用多普勒估计的速度进行坐标更新。
将求得的速度代入卡尔曼滤波状态预报部分,完成状态预测。滤波的状态方程和观测方程为:
| $ \left\{\begin{array}{l} \bar{X}_{t_n}=\hat{X}_{t_{n-1}}+\Delta \hat{X}_{t_n, t_{n-1}}+\omega_{t_n, t_{n-1}} \\ \bar{L}_{t_n}^{\mathrm{s}, \mathrm{r}}=\boldsymbol{A}_{t_n} \bar{X}_{t_n}+v_{t_n} \end{array}\right. $ | (20) |
式中,
为验证载波相位平滑伪距、多普勒平滑伪距和历元间速度约束的平滑定位算法在低成本接收机GNSS定位中的实际效果,本文设计静态定位(实验1)和动态定位(实验2)2组测试实验,其中动态定位分为开阔环境和遮挡环境。在实验1和实验2中,分别对原始伪距定位(方案1)、载波相位平滑伪距定位(方案2)、多普勒平滑伪距定位(方案3)和历元间速度约束的平滑定位算法(方案4)进行精度对比。实验使用国产手机小米8、华为P40和专业天线一体化接收机,采样间隔为1 s。将小米8、华为P40和专业天线一体化接收机并排摆放,以获取静态数据;将小米8、华为P40和专业天线一体化接收机捆绑在一起举高步行,以获取动态数据。
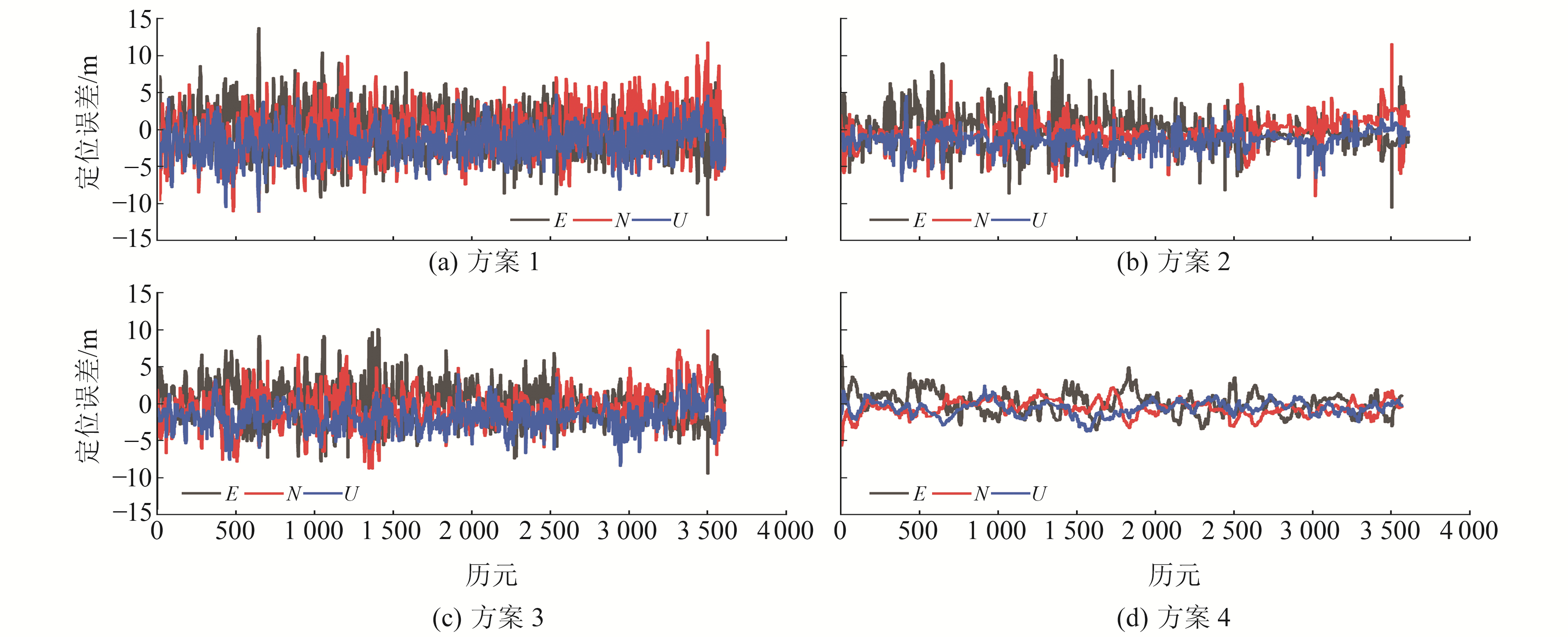
3.1 静态实验分析图 1~4为静态环境下小米8和华为P40伪距平滑的结果。手机的伪距观测值受多路径等误差影响较为严重,数据质量较差,以专业天线一体化接收机为基准,手机的抗差伪距精度达15 m。由图 1可见,小米8的3种伪距平滑方法精度均有所提升,其中载波相位平滑伪距和多普勒平滑伪距精度提升较小,历元间变化约束平滑伪距定位精度有明显提升。抗差伪距在3 250~3 700历元间的误差精度有较大波动,伪距观测值精度较差。在此期间3种平滑伪距均受到影响,其中历元间变化约束平滑伪距受到影响较小,载波和多普勒平滑伪距受影响较大,产生较大波动。

|
图 1 小米8多种平滑定位结果误差序列 Fig. 1 Error sequence of multiple smooth positioning results of Mi 8 |
|
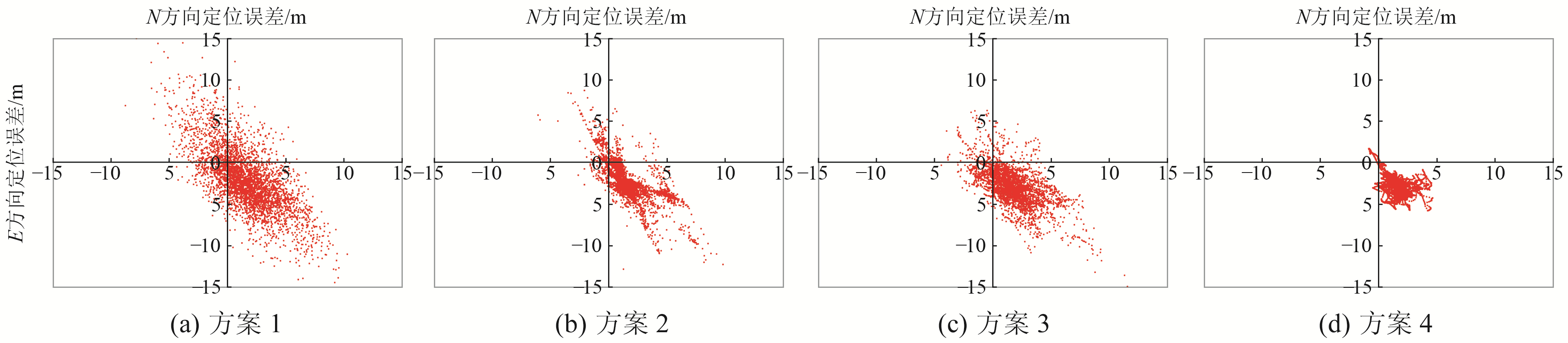
图 2 小米8多种平滑定位平面误差 Fig. 2 Various smooth positioning plane errors of Mi 8 |
|
图 3 华为P40多种平滑定位结果误差序列 Fig. 3 Error sequence of multiple smooth positioning results of Huawei P40 |
|
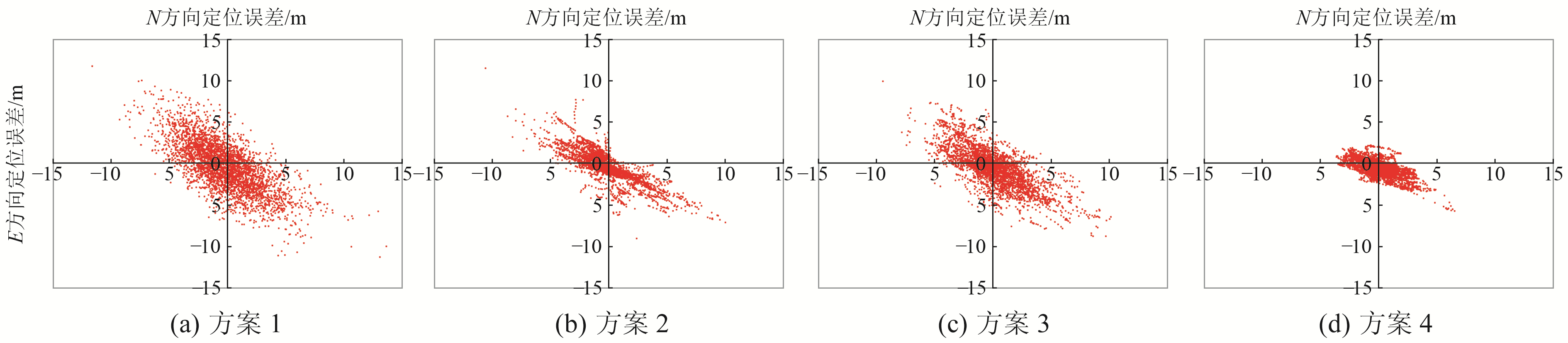
图 4 华为P40多种平滑定位平面误差 Fig. 4 Varions smooth positioning plane errors of Huawei P40 |
由图 2可见,抗差伪距的水平定位误差分布范围较广,点位误差较为分散,有较多点的精度超过10 m;载波和多普勒平滑得到改善,大部分精度在8 m以内;历元间变化约束平滑伪距精度更优,可以达到5 m以内,且分布集中,没有飞点。
由图 3和4可见,华为P40与小米8定位结果整体相当,经过载波相位与多普勒平滑后整体误差有一定的改善,误差趋势变缓,但整体误差波动仍然较大,使用位置变化约束后3个方向上的误差大部分控制在5 m以内。
由表 1(单位m)可见,小米8和华为P40平滑后精度均有所提升。小米8载波平滑后在水平、高程方向上的精度分别提升1.25 m、1.12 m,多普勒平滑后在水平、高程方向上的精度分别提升0.76 m和0.73 m;华为P40载波平滑后在水平、高程方向上的精度分别提升1.17 m、0.70 m,多普勒平滑后在水平、高程方向上的精度分别提升0.56 m和0.28 m。静态环境下,智能手机的载波相位较为稳定,载波平滑结果要优于多普勒平滑。历元间位置约束平滑的提升效果最好,小米8智能终端在水平方向上提升1.49 m、高程方向上提升1.38 m;华为P40智能终端提升效果最为明显,在水平方向上提升2.11 m、高程方向上提升1.53 m。
|
|
表 1 智能手机静态平滑定位误差统计 Tab. 1 Statistics of static smooth positioning error of smart phones |
动态实验场所为学校,采集地点为有林荫遮挡的林间小路,测量数据前将手机与专业天线一体化接收机捆绑在一起。无论是静态实验还是动态实验,载波平滑伪距和多普勒平滑伪距效果相近,且皆优于抗差伪距,但差于速度约束。因此本文不再对载波和多普勒平滑伪距展开实验,仅采用抗差伪距和速度约束平滑伪距进行解算,并进行单、双频的精度对比,结果见图 5~8。
|
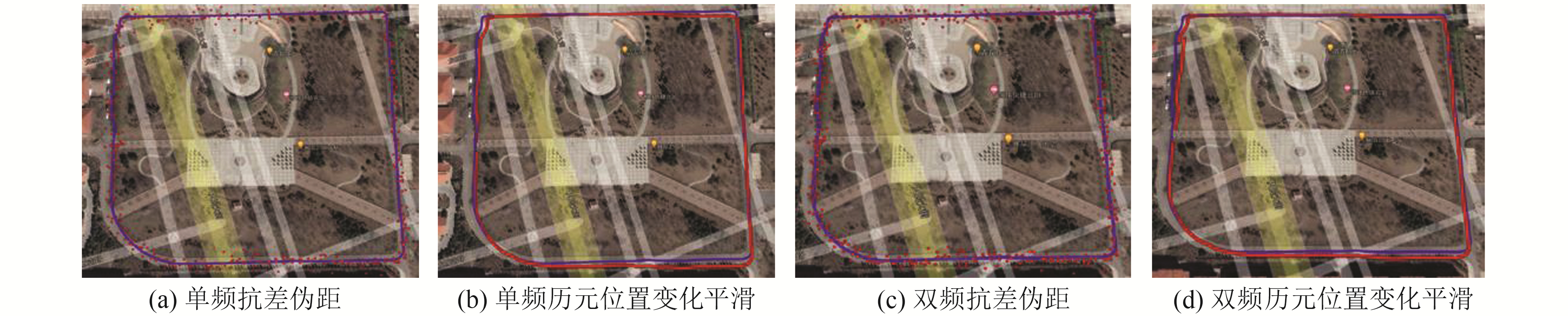
图 5 小米8单、双频历元间位置平滑定位轨迹 Fig. 5 Position smooth positioning track between Mi 8 single and dual frequency epochs |
|
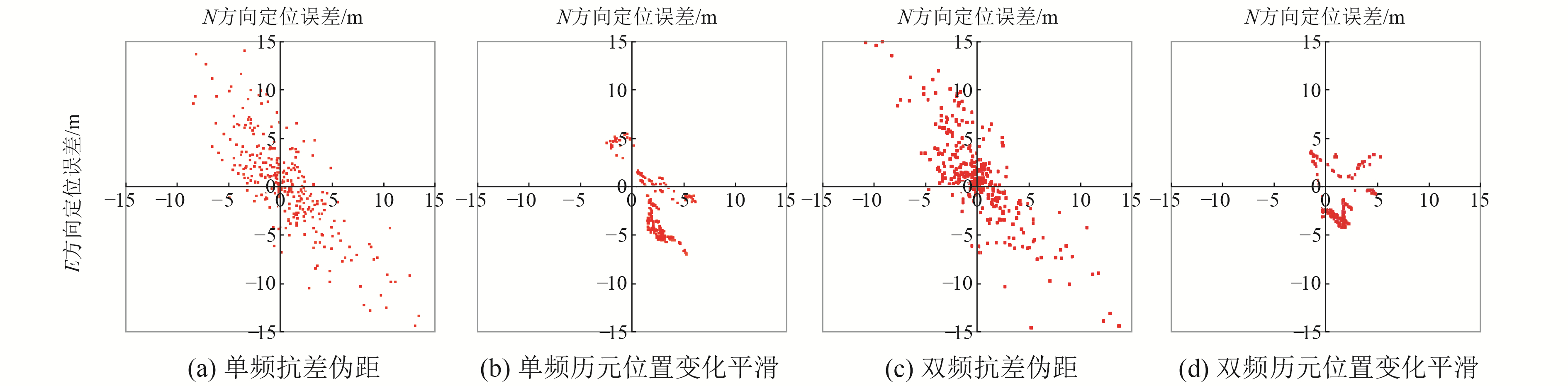
图 6 小米8单、双频水平方向定位误差 Fig. 6 Mi 8 single and dual frequency plane positioning errors |

|
图 7 华为P40单、双频历元间位置平滑定位轨迹 Fig. 7 Position smooth positioning track between Huawei P40 single and dual frequency epochs |
|
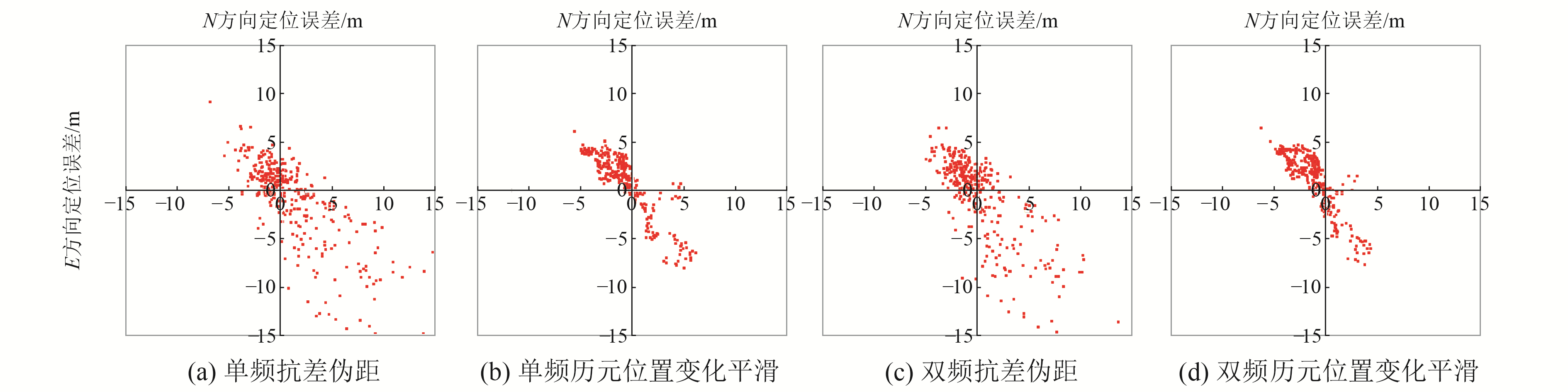
图 8 华为P40单、双频水平方向定位误差 Fig. 8 Huawei P40 single and dual frequency plane positioning errors |
由图 5可见,本组数据中,小米8经过抗差处理后依旧有很多飞点,其中大量飞点集中在教学楼附近,整体轨迹不够清晰。这是因为教学楼会造成较为严重的多路径效应,伪距噪声增大,从而严重影响伪距观测值的质量。经过历元间变化约束平滑后的定位轨迹精度得到较大提升,轨迹清晰明显,且解算点位的连续性更佳。
由图 6可见,单频抗差伪距水平方向定位误差在15 m以内,且飞点较多,点位分布分散;经过历元间变化平滑后,水平方向误差明显减小,基本控制在8 m以内,点位分布更加集中,飞点明显减少。双频定位精度较单频有所提升,抗差伪距水平方向定位误差在12 m以内,历元间变化平滑水平方向误差在5 m以内。
由图 7可见,与小米8相比,华为P40经过抗差伪距处理后飞点较少,点位在靠近教学楼和弯道附近均匀分布。
由图 8可见,华为P40经过抗差伪距处理后大多数点位水平方向误差在7 m以内,部分点位水平方向误差在8~15 m之间。经位置平滑后,飞点数量明显减少,水平方向定位误差在6 m以内。频率增加后水平方向定位误差有微小提升,点位分布更加集中。
在动态半遮挡的林荫环境下,华为P40和小米8经位置平滑后的精度均有所提升,但弯道处的抗差伪距解同标准轨道相差甚远,在一些直线路段也存在较多跳动。而经过历元间位置变化平滑后,直线路段轨迹更加平滑,弯道处也更接近于参考点位,轨迹更加明显。由表 2(单位m)可知,单频条件下,小米8的水平方向定位精度提升1.75 m,华为P40的水平方向定位精度提升2.58 m;双频条件下,小米8的水平方向定位精度提升2.89 m,华为P40的水平方向定位精度提升2.23 m。对比华为P40和小米8可知,华为P40的抗差效果要优于小米8,受多路径误差影响较小,相较于小米8更加稳定。
|
|
表 2 智能手机动态平滑定位误差统计 Tab. 2 Statistics of smart phone dynamic smooth positioning error |
本文以小米8和华为P40为研究对象,分析静态开阔环境和动态半遮挡环境下抗差伪距、载波平滑伪距、多普勒平滑伪距和历元间位置变化约束平滑伪距的定位精度。结果如下:
1) 静态开阔环境下小米8的多普勒平滑伪距定位误差相比于抗差伪距有所提升,且点位分布均匀、较为稳定;载波平滑伪距误差精度提升效果优于多普勒平滑伪距,但会受到环境影响产生波动;历元间位置变化约束平滑效果最好,在水平和高程方向上的精度分别提升1.49 m和1.38 m;动态半遮挡环境下小米8单频位置平滑伪距的水平方向定位误差提升1.75 m,双频比单频更加稳定,水平方向定位误差提升1.41 m。
2) 相比于小米8,华为P40的提升效果更加明显,静态环境下位置平滑的水平方向误差提升2.11 m,高程方向误差提升1.53 m,定位误差相比于小米8分别提升1.75 m和0.64 m;动态半遮挡环境下华为P40单频位置平滑伪距的水平方向误差提升2.58 m,双频的提升效果差于小米8,水平方向误差精度仅提升0.11 m。
通过上述分析可以看出,历元间位置变化约束相较于抗差伪距在精度上已有较大提升,但在速度方面还有改进空间。INS与GNSS具有很强的互补性,且INS在速度方面具有更广泛的应用前景,可将其组成设备安装在载体内,获取载体的加速度。对加速度进行积分运算,可进一步获取载体的瞬时姿态、速度及位置信息,有较为广阔的研究前景。
| [1] |
Geng J H, Jiang E M, Li G C, et al. An Improved Hatch Filter Algorithm towards Sub-Meter Positioning Using only Android Raw GNSS Measurements without External Augmentation Corrections[J]. Remote Sensing, 2019, 11(14): 1 679 DOI:10.3390/rs11141679
(  0) 0) |
| [2] |
Hatch R. The Synergism of GPS Code and Carrier Measurements[C]. International Geodetic Symposium on Satellite Doppler Positioning, New Mexico, 1983
(  0) 0) |
| [3] |
何海波, 杨元喜, 孙中苗, 等. GPS多普勒频移测量速度模型与误差分析[J]. 测绘学院学报, 2003, 20(2): 79-82 (He Haibo, Yang Yuanxi, Sun Zhongmiao, et al. Mathematic Model and Error Analyses for Velocity Determination Using GPS Doppler Measurements[J]. Journal of Institute of Surveying and Mapping, 2003, 20(2): 79-82)
(  0) 0) |
| [4] |
Jing S R, Xu B, Yong L, et al. Doppler-Aided Rapid Positioning Method for BDS Receivers[J]. Electronics Letters, 2015, 51(25): 2 139-2 141 DOI:10.1049/el.2015.1033
(  0) 0) |
| [5] |
Pesyna K M, Heath R W, Humphreys T E. Centimeter Positioning with a Smartphone-Quality GNSS Antenna[C]. 27th International Technical Meeting of the Satellite Division of The Institute of Navigation, Florida, 2014
(  0) 0) |
| [6] |
Wang X X, Tu R, Gao Y P, et al. Velocity Estimations by Combining Time-Differenced GPS and Doppler Observations[J]. Measurement Science and Technology, 2019, 30(12): 125 003 DOI:10.1088/1361-6501/ab375f
(  0) 0) |
| [7] |
Zhang X H, Guo B F, Guo F, et al. Influence of Clock Jump on the Velocity and Acceleration Estimation with a Single GPS Receiver Based on Carrier-Phase-Derived Doppler[J]. GPS Solutions, 2013, 17(4): 549-559 DOI:10.1007/s10291-012-0300-x
(  0) 0) |
| [8] |
Zhang Y, Cai C, Sun Q, et al. Accuracy Analysis of Single Point Positioning Using Doppler Smoothed Pseudorange Observations[J]. Geomatics Science and Technology, 2017, 5(3): 152-157 DOI:10.12677/GST.2017.53018
(  0) 0) |
| [9] |
史翔. 基于智能手机GNSS观测值的连续平滑定位算法[D]. 武汉: 武汉大学, 2019 (Shi Xiang. Continuous Smooth Positioning Algorithm Based on GNSS Observations of Smartphones[D]. Wuhan: Wuhan University, 2019)
(  0) 0) |
| [10] |
肖青怀, 谷守周, 秘金钟, 等. 智能手机多普勒平滑伪距单点定位精度分析[J]. 测绘科学, 2020, 45(7): 11-17 (Xiao Qinghuai, Gu Shouzhou, Bei Jinzhong, et al. Doppler Smoothed Pseudorange Single Point Positioning Accuracy Analysis for Smartphones[J]. Science of Surveying and Mapping, 2020, 45(7): 11-17)
(  0) 0) |
| [11] |
周厚香. 基于单频低成本接收机的定位算法研究[D]. 北京: 中国地质大学(北京), 2020 (Zhou Houxiang. Research on Positioning Algorithm Based on Single-Frequency Low-Cost Receiver[D]. Beijing: China University of Geosciences, 2020)
(  0) 0) |
| [12] |
祝会忠, 雷啸挺, 李军, 等. BDS参考站三频整周模糊度单历元确定方法[J]. 测绘学报, 2020, 49(11): 1 388-1 398 (Zhu Huizhong, Lei Xiaoting, Li Jun, et al. The Algorithm of Integer Ambiguity Resolution with BDS Triple-Frequency between Reference Stations at Single Epoch[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(11): 1 388-1 398)
(  0) 0) |
| [13] |
祝会忠, 雷啸挺, 徐爱功, 等. 顾及GEO卫星约束的长距离BDS三频整周模糊度解算[J]. 测绘学报, 2020, 49(9): 1 222-1 234 (Zhu Huizhong, Lei Xiaoting, Xu Aigong, et al. The Integer Ambiguity Resolution of BDS Triple-Frequency between Long Range Stations with GEO Satellite Constraints[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1 222-1 234)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43

