2. 武汉大学测绘学院,武汉市珞喻路129号,430079
目前GPS站监测到的季节性变化(如强年周期信号)主要为地表质量迁移驱动下的非构造站点运动[1]。在进行GPS站坐标分量运动特征分析时,若忽略环境负荷效应(如大气、海洋、水文等)引起的非线性变化,将导致垂向速度和误差估计出现显著偏差[2]。王敏等[3]利用负荷形变修正GPS数据后发现,垂向位移的RMS减小约1 mm,同时负荷修正可降低垂向位移中13%~22%的季节性振幅[4]。然而,已有研究仅能给出不同地表质量负荷修正引起的GPS测站位移及其季节性振幅变化,并未涉及负荷修正对测站时序噪声特征的影响。李昭等[5]采用多种组合噪声模型对GPS站时序噪声特性进行分析,同时计算大气压、积雪深度以及土壤湿度负荷等对GPS测站位移的影响后认为,GPS站时序噪声主要表现为闪烁噪声+白噪声和带通幂律噪声+白噪声;Kargoll等[6]利用AR模型对GPS垂向噪声序列进行建模,并指出有色噪声可通过自回归系数进行参数化改正。
在噪声模型方面,可利用AR模型分析GPS测站的有色噪声,该模型运用灵活、方便,且与自协方差和功率谱密度之间存在直接转化关系[6]。但AR模型严格假设白噪声为同方差噪声,难以反映方差的真实特性。因此,本文提出一种描述噪声时间相关和异方差特性的时序噪声建模策略:首先采用轨迹模型和AR模型建立GPS坐标时序模型,以模型化残差序列为研究对象,采用自回归条件异方差(autoregressive conditional heteroscedasticity, ARCH)检验法[7]判断残差序列的异方差特性;然后利用AR-GARCH模型[7]建立时序噪声模型;最后通过实测算例分析负荷修正前后不同噪声模型之间的估计差异,并进一步验证GPS坐标时间序列中白噪声的异方差特性。
1 地表质量负荷效应GPS站坐标时间序列包含地表弹性信号和深层构造信号。本文首先采用TSAnalyzer软件[8]对GPS数据进行粗差探测和阶跃项修复,然后利用德国地球科学研究中心GFZ提供的负荷格林函数法计算负荷形变。由于大气、非潮汐海洋和水文负荷的时间分辨率分别为3 h、3 h和24 h,空间分辨率均为0.5°×0.5°,因此在对比和修正GPS时间序列时需对负荷数据进行降采样处理,以获取单日的地表负荷形变。
2 GPS坐标时间序列分析 2.1 时间序列模型在对GPS站坐标时间序列进行粗差探测和阶跃项修复后,轨迹模型[2]可简化为:
| $ \left\{\begin{array}{l} y_i=\boldsymbol{A}_i \boldsymbol{\xi}+\varepsilon_i \\ \boldsymbol{A}_i \xi=y_0+v t_i+\sum\limits_{j=1}^{m_s} a_j \sin \omega_j t_i+ \\ \;\;\;\;b_j \cos \omega_j t_i \end{array}\right. $ | (1) |
式中,yi为ti(i=1, ⋯, n)时刻的单分量位移,n为总观测长度;εi为有色噪声;y0和v分别为截距和斜率;aj和bj分别为第j个谐波中sin和cos函数的振幅;ωj为角频率;ms为谐波总个数;ξ =[y0, v, a1, b1, ω1, ⋯, ams, bms, ωms]T为(m×1)维待估参数;
考虑到εi的时间相关性,建立AR模型[6]:
| $ \left[\begin{array}{c} \varepsilon_{d+1} \\ \varepsilon_{d+2} \\ \vdots \\ \varepsilon_n \end{array}\right]=\left[\begin{array}{cccc} \varepsilon_d & \varepsilon_{d-1} & \cdots & \varepsilon_1 \\ \varepsilon_{d+1} & \varepsilon_d & \cdots & \varepsilon_2 \\ \vdots & \vdots & \ddots & \vdots \\ \varepsilon_{n-1} & \varepsilon_{n-2} & \cdots & \varepsilon_{n-d} \end{array}\right]\left[\begin{array}{c} \varphi_1 \\ \varphi_2 \\ \vdots \\ \varphi_d \end{array}\right]+\left[\begin{array}{c} e_{d+1} \\ e_{d+2} \\ \vdots \\ e_n \end{array}\right] $ | (2) |
式中,{εi}为有色噪声序列;
若序列随时间的变化值波动幅度较大,则称序列具有异方差特性。本文采用GARCH模型建立ei的异方差σi2,即
| $ \left\{\begin{array}{l} e_i \mid \boldsymbol{m} \sim N\left(0, \sigma_i^2\right) \\ \sigma_i^2=\alpha_0+\sum\limits_{s=1}^q \alpha_s e_{i-s}^2+\sum\limits_{l=1}^p \beta_l \sigma_{i-l}^2 \end{array}\right. $ | (3) |
式中,
采用ARCH检验法鉴别同方差与异方差之间的差异。该检验方法要求序列至少满足原假设H0: αs=βl=0和备选假设Ha: αs≥0, βl≥0中的一种情况。为进行定量判断,构建lm检验统计量为:
| $ l m^{\prime}=\frac{N \hat{\boldsymbol{K}}^{\mathrm{T}} \hat{\boldsymbol{z}}\left(\hat{\boldsymbol{z}}^{\mathrm{T}} \hat{\boldsymbol{z}}\right)^{-1} \hat{\boldsymbol{z}}^{\mathrm{T}} \hat{\boldsymbol{K}}}{\hat{\boldsymbol{K}}^{\mathrm{T}} \hat{\boldsymbol{K}}}=N R^2 $ | (4) |
式中,
联立式(1)~(3)可得yi的对数似然函数:
| $ \begin{array}{l} \log l_M=-\frac{N}{2} \log 2 \pi-\frac{1}{2} \sum\limits_{i=d+1}^n \log \sigma_i^2- \\ \;\;\;\sum\limits_{i=d+1}^n \frac{\left(\varepsilon_i-\varphi_1 \varepsilon_{i-1}-\cdots-\varphi_d \varepsilon_{i-d}\right)^2}{2 \sigma_i^2} \end{array} $ | (5) |
分别对参数ξ、φ和λ求导并令其等于0:
| $ \left\{\begin{array}{l} \boldsymbol{0}=\sum\limits_{i=d+1}^n\left[\frac{e_i^2}{2 \sigma_i^4}-\frac{1}{2 \sigma_i^2}\right]\left[\frac{\partial \sigma_i^2}{\partial \boldsymbol{\xi}}\right]^{\mathrm{T}}-\frac{e_i}{\sigma_i^2}\left[\frac{\partial e_i}{\partial \boldsymbol{\xi}}\right]^{\mathrm{T}} \\ \boldsymbol{0}=-\sum\limits_{i=d+1}^n \frac{e_i}{\sigma_i^2}\left[\frac{\partial e_i}{\partial \boldsymbol{\varphi}}\right]^{\mathrm{T}} \\ \boldsymbol{0}=\sum\limits_{i=d+1}^n\left[\frac{e_i^2}{2 \sigma_i^4}-\frac{1}{2 \sigma_i^2}\right]\left[\frac{\partial \sigma_i^2}{\partial \boldsymbol{\lambda}}\right]^{\mathrm{T}} \end{array}\right. $ | (6) |
为方便符号表示,将式(6)中部分项定义为:
| $ \left\{\begin{array}{l} \boldsymbol{J}_i=-\frac{\partial e_i}{\partial \boldsymbol{\xi}}=\boldsymbol{A}_i-\sum\limits_{h=1}^d \varphi_h \boldsymbol{A}_{i-h}, \\ \;\;\;\;p_i=\frac{1}{\sigma_i^2}, p_i^{\prime}=\frac{1}{2 \sigma_i^4} \\ \boldsymbol{J}_i^{\prime}=\frac{\partial \sigma_i^2}{\partial \boldsymbol{\xi}}=2 \sum\limits_{s=1}^q \alpha_s e_{i-s} \frac{\partial e_{i-s}}{\partial \boldsymbol{\xi}}+ \\ \;\;\;\;\sum\limits_{l=1}^p \beta_l \frac{\partial \sigma_{i-l}^2}{\partial \boldsymbol{\xi}} \\ \boldsymbol{B}_i=\frac{\partial e_i}{\partial \boldsymbol{\varphi}}=-\left[\varepsilon_{i-1}, \varepsilon_{i-2}, \cdots, \varepsilon_{i-d}\right] \\ \boldsymbol{U}_i=\frac{\partial \sigma_i^2}{\partial \boldsymbol{\lambda}} \end{array}\right. $ | (7) |
将式(7)代入式(6)可化简得到:
| $ \left\{\begin{array}{l} \eta(\boldsymbol{\xi})=\sum\limits_{i=d+1}^n p_i \boldsymbol{J}_i^{\mathrm{T}} e_i+p_i^{\prime} \boldsymbol{J}_i^{\prime \mathrm{T}}\left(e_i^2-\sigma_i^2\right) \\ \;\;\;\sum\limits_{i=d+1}^n \hat{p}_i \hat{\boldsymbol{B}}_i^{\mathrm{T}} \hat{e}_i=\boldsymbol{0} \\ \eta(\boldsymbol{\lambda})=\sum\limits_{i=d+1}^n-p_i^{\prime} \boldsymbol{U}_i^{\mathrm{T}} \sigma_i^2+p_i^{\prime} \boldsymbol{U}_i^{\mathrm{T}} e_i^2 \end{array}\right. $ | (8) |
由于直接求解ξ和λ较为困难,因此借助线性近似方法,将η(ξ)和η(λ)在近似值
| $ \left\{\begin{array}{l} \eta(\boldsymbol{\xi}) \approx \ell(\widetilde{\boldsymbol{\xi}})+h(\tilde{\boldsymbol{\xi}}) \Delta \boldsymbol{\xi}=h(\widetilde{\boldsymbol{\xi}}) \Delta \boldsymbol{\xi} \\ \eta(\boldsymbol{\lambda}) \approx \ell(\tilde{\boldsymbol{\lambda}})+h(\tilde{\boldsymbol{\lambda}}) \Delta \boldsymbol{\lambda}=h(\tilde{\boldsymbol{\lambda}}) \Delta \boldsymbol{\lambda} \end{array}\right. $ | (9) |
联立式(6)、(7)、(9),并令
| $ \left\{\begin{array}{l} \sum\limits_{i=d+1}^n \hat{p}_i \hat{\boldsymbol{J}}_i^{\mathrm{T}}\left(\hat{\boldsymbol{J}}_i \hat{\boldsymbol{\xi}}-l_i\right)+\hat{p}_i^{\prime} \hat{\boldsymbol{J}}_i^{\prime \mathrm{T}}\left(\hat{\boldsymbol{J}}_i^{\prime} \hat{\boldsymbol{\xi}}-l_i^{\prime}\right)=\boldsymbol{0} \\ \sum\limits_{i=d+1}^n \hat{p}_i^{\prime} \boldsymbol{U}_i^{\mathrm{T}} \boldsymbol{U}_i \Delta \boldsymbol{\lambda}+\hat{p}_i^{\prime} \boldsymbol{U}_i^{\mathrm{T}}\left(\hat{\sigma}_i^2-\hat{e}_i^2\right)=\boldsymbol{0} \end{array}\right. $ | (10) |
由式(8)和式(10)可得参数ξ、φ和λ的估计式为:
| $ \begin{aligned} \hat{\boldsymbol{\xi}}= & \left(\sum\limits_{i=d+1}^n \hat{p}_i \hat{\boldsymbol{J}}_i^{\mathrm{T}} \hat{\boldsymbol{J}}_i+\hat{p}_i^{\prime} \hat{\boldsymbol{J}}_i^{\prime \mathrm{T}} \hat{\boldsymbol{J}}_i^{\prime}\right)^{-1} \cdot \\ & \left(\sum\limits_{i=d+1}^n \hat{p}_i \hat{\boldsymbol{J}}_i^{\mathrm{T}} \hat{l}_i+\hat{p}_i^{\prime} \hat{\boldsymbol{J}}_i^{\prime \mathrm{T}} \hat{l}_i^{\prime}\right) \end{aligned} $ | (11) |
| $ \hat{\boldsymbol{\varphi}}=\left(\sum\limits_{i=d+1}^n \hat{p}_i \hat{\boldsymbol{B}}_i^{\mathrm{T}} \hat{\boldsymbol{B}}_i\right)^{-1} \sum\limits_{i=d+1}^n \hat{p}_i \hat{\boldsymbol{B}}_i^{\mathrm{T}}\left(y_i-\boldsymbol{A}_i \hat{\boldsymbol{\xi}}\right) $ | (12) |
| $ \hat{\boldsymbol{\lambda}}=\left(\sum\limits_{i=d+1}^n \hat{p}_i^{\prime} \hat{\boldsymbol{U}}_i^{\mathrm{T}} \hat{\boldsymbol{U}}_i\right)^{-1} \sum\limits_{i=d+1}^n \hat{p}_i^{\prime} \hat{\boldsymbol{U}}_i^{\mathrm{T}}\left(\hat{\boldsymbol{U}}_i \hat{\boldsymbol{\lambda}}+\hat{e}_i^2-\hat{\sigma}_i^2\right) $ | (13) |
同时,条件方差估计为:
| $ \hat{\sigma}_i^2=\hat{\alpha}_0+\sum\limits_{s=1}^q \hat{\alpha}_s \hat{e}_{i-s}^2+\sum\limits_{l=1}^p \hat{\beta}_l \hat{\sigma}_{i-l}^2 $ | (14) |
得到参数估值
由于GPS坐标时间序列可能存在缺失,为克服AR或AR-GARCH(AG)模型只能对均匀序列建模这一缺陷,本文利用填补法将对数似然函数重写为:
| $ \begin{array}{c} \log l_M=-\frac{N-\gamma}{2} \log 2 \pi+ \\ \sum\limits_{i \in C_o}-\frac{1}{2} \log \sigma_i^2+\frac{e_i^2}{2 \sigma_i^2} \end{array} $ | (15) |
式中,Co为观测数据的样本空间;γ为缺失数据的个数。式(15)中白噪声ei为:
| $ e_i=y_i-\boldsymbol{A}_i \boldsymbol{\xi}-\sum\limits_{h=1}^d \varphi_h y_{i-h}+\sum\limits_{h=1}^d \varphi_h \boldsymbol{A}_{i-h} \boldsymbol{\xi} $ | (16) |
令
则有:
| $ e_i^2=y_i^2-2 G_i(\boldsymbol{m}) y_i+G_i^2(\boldsymbol{m}) $ | (17) |
为填补缺失数据yi,计算条件期望:
| $ \hat{y}_i=E\left(y_i \mid\left\{y_i, i \in C_o\right\}, \hat{\boldsymbol{m}}\right)=G_i(\hat{\boldsymbol{m}}) $ | (18) |
| $ \hat{y}_i^2=E\left(y_i^2 \mid\left\{y_i, i \in C_o\right\}, \hat{\boldsymbol{m}}\right)=\hat{\sigma}_i^2+G_i^2(\hat{\boldsymbol{m}}) $ | (19) |
由此可计算出缺失数据及其平方项。通过§2.3中参数估计流程可计算出模型参数,具体算法流程见图 1。此外,白噪声幅度的计算公式为:
| $ \hat{\sigma}_e^2=\frac{1}{\sum\limits_{i \in C_o} \hat{p}_i} \sum\limits_{i \in C_o} \hat{p}_i \hat{e}_i^2 $ | (20) |

|
图 1 基于AG模型的参数估计流程 Fig. 1 Flowchart of the parameter estimation based on the AG model |
为验证本文方法的有效性,设计蒙特卡洛仿真实验和GPS坐标时间序列实测算例。
3.1 蒙特卡洛仿真实验仿真生成含有线性趋势、年周期和半年周期信号及AG噪声过程的时间序列,采用AR(4)-GARCH(1, 1)模型:
| $ \left\{\begin{array}{l} \varepsilon_i =-0.2 \varepsilon_{i-1}+0.005 \varepsilon_{i-2}+ \\ \;\;\;\;0.3 \varepsilon_{i-3}-0.4 \varepsilon_{i-4}+e_i \\ e_i \sim N\left(0, \sigma_i^2\right) \\ \sigma_i^2 =0.000\;002+0.2 e_{i-1}^2+0.6 \sigma_{i-1}^2 \end{array}\right. $ | (21) |
年周期和半年周期振幅通过均匀分布随机产生,区间设置见表 1。时间序列长度设置为3 000 d、6 000 d和9 000 d,各生成500组仿真时间序列,期间无数据缺失。采用本文方法计算的部分参数y0、v、φ1、α0见图 2。
|
|
表 1 参数设置 Tab. 1 Parameter settings |

|
图 2 不同时间序列长度的部分参数估值 Fig. 2 Some parameter estimates for time series with different time lengths |
由图 2可见,蒙特卡洛仿真实验得到的参数统计结果近似呈正态分布,且未出现显著的偏尾特征,说明参数的验后分布与白噪声的概率分布特征相近。该现象表明,即使噪声具有非高斯特性,参数验后也并不一定呈非正态分布。此外,从参数随时间长度的变化幅度上看,在同等噪声水平下,速度v受时间序列长度的影响较大,但其相对变化值较小,说明其准确性较高;其他参数随时间序列的变化幅度略有不同。
3.2 实测算例本文选取中国地壳运动观测网络I期中4个基准站数据(BJFS、HRBN、KMIN和YANC测站),时间跨度为1999~2020年,采用GAMIT/GLOBK软件进行解算。利用单日负荷形变对坐标时间序列进行修正,负荷总幅度(大气+非潮汐海洋+水文)及修正效果分别采用RMS和WRMS差值[5]进行评估,结果见表 2(单位mm)。由表可见,4个台站垂直分量上的RMS和WRMS差值分别为水平分量的4~9倍和6~8倍,修正效果较为显著。
|
|
表 2 RMS和WRMS差值 Tab. 2 RMS and WRMS difference |
为确定AR及AG模型的最佳阶数,采用改进的贝叶斯信息准则进行评估[10]:
| $ \mathrm{BIC}_{-} \mathrm{tp}=-2 \log l_M+\log \frac{N-\gamma}{2 \pi} M $ | (22) |
式中,M为参数的总个数;lM为似然函数,其形式按是否存在缺失数据分为式(5)和式(15)。由于BIC仅在观测数(N-γ)相当大时效果最佳,因此为了避免近似情况出现,在BIC_tp中引入缩放因子2π。
采用BIC_tp确定负荷修正前(实线)和修正后(虚线)AR和AG模型的最优阶数(图 3),由图可见,2种模型得到的最优阶数d约为10。负荷修正后,BJFS和HRBN测站的垂直分量中d值增加较为明显,说明噪声表现出更为显著的长记忆性[6]。

|
图 3 AR和AG模型的最优阶数 Fig. 3 Optimal order of AR and AG models |
本文分别给出闪烁噪声+白噪声(FN+WN)模型和AR模型的计算结果与AG模型进行比较,FN+WN模型采用LS-VCE[11]修正先验协因数矩阵。假设纯白噪声模型下BIC_tp=0,计算FN+WN、AR和AG噪声模型与白噪声模型的BIC_tp差值,结果如表 3所示,其中BIC_tp差值越小,噪声模型越优。由表可见,负荷修正前后不同噪声模型的BIC_tp差值及其均值略有差异,但AG模型的BIC_tp差值及其均值最小,而AR模型略小于FN+WN模型。由此可知,AG模型在描述GPS时序噪声特性方面具有一定的优越性。
|
|
表 3 同噪声模型与白噪声模型(BIC_tp = 0)的BIC_tp差值 Tab. 3 Difference of the BIC_tp between different noise models and white noise model (BIC_tp = 0) |
为量化负荷修正前后不同噪声模型估计的白噪声含量变化趋势,对负荷修正前后得到的白噪声幅度值作差。由图 4可见,相比于垂直分量,各台站水平分量的白噪声幅度差变化较小,FN+WN模型计算的幅度差负值居多,说明负荷修正后白噪声幅度增加,负荷修正前白噪声含量被低估。AR和AG模型的幅度差均为正值,说明二者均能反映出负荷修正后白噪声含量的减少情况。
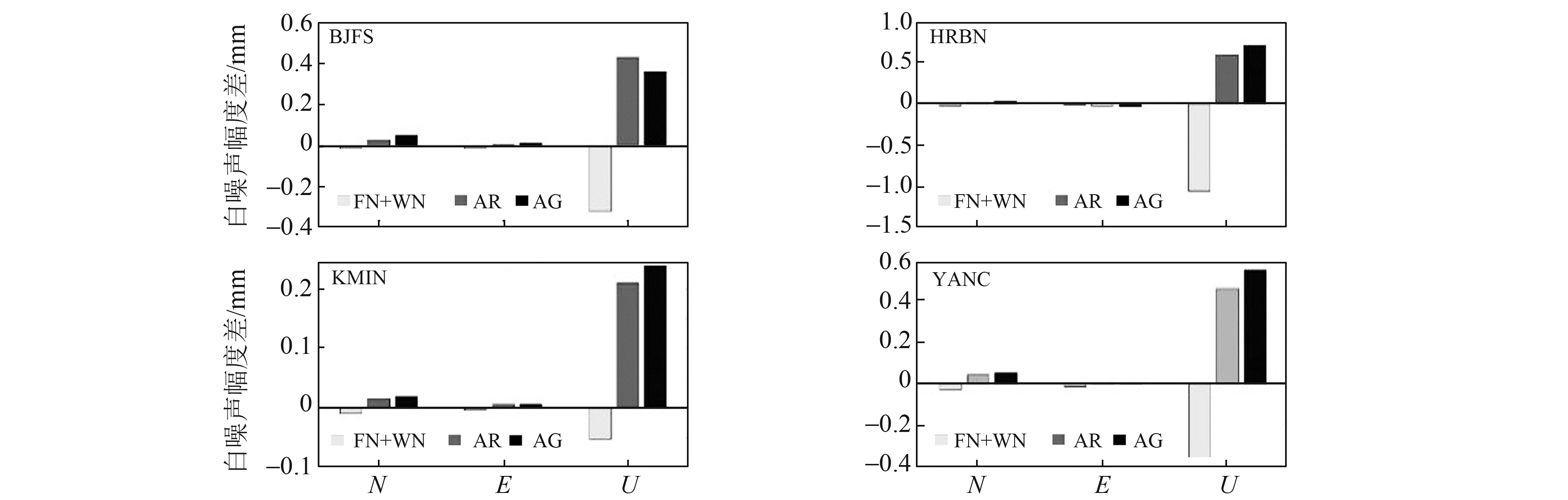
|
图 4 负荷修正前后不同噪声模型估计的白噪声幅度差 Fig. 4 White noise amplitude difference estimated by different noise models before and after load corrections |
负荷修正后,4种噪声模型计算的白噪声幅度见表 4(单位mm)。由表可见,不同噪声模型在垂直分量上的白噪声幅度约为水平分量上的2~4倍。
|
|
表 4 负荷修正后4种噪声模型估计的白噪声幅度 Tab. 4 White noise amplitude estimated by four noise models after load corrections |
负荷修正后AG模型估计的白噪声条件标准差(深灰色实线)见图 5,其中绿色圆圈为缺失位置估值,红色实线为负荷修正前后白噪声条件标准差差值。由图可见,检验统计量均大于临界值,因此原假设不成立,说明负荷修正前后白噪声均存在异方差特性。

|
图 5 负荷修正前后AG模型估计的白噪声条件标准差及差值 Fig. 5 Estimation of conditional standard deviation and its difference of white noise by AG model before and after load corrections |
1) 本文考虑多种负荷效应对GPS坐标时间序列及噪声估计的影响。结果表明,负荷形变以垂直分量贡献为主,水平分量上贡献较小。负荷修正后,时间序列噪声含量有所降低,噪声表现出更为显著的长记忆性,主要分布于垂直分量上。
2) 构建一种描述噪声时间相关和异方差特性的AR-GARCH噪声模型,结果表明,GPS坐标时间序列的白噪声具有显著的异方差特性。此外,本文构建的AG模型优于FN+WN及AR模型,可为GPS时序噪声建模提供新思路。
| [1] |
姜卫平, 王锴华, 李昭, 等. GNSS坐标时间序列分析理论与方法及展望[J]. 武汉大学学报: 信息科学版, 2018, 43(12): 2 112-2 123 (Jiang Weiping, Wang Kaihua, Li Zhao, et al. Prospect and Theory of GNSS Coordinate Time Series Analysis[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 2 112-2 123)
(  0) 0) |
| [2] |
Blewitt G, Lavallée D. Effect of Annual Signals on Geodetic Velocity[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B7): 2 145
(  0) 0) |
| [3] |
王敏, 沈正康, 董大南. 非构造形变对GPS连续站位置时间序列的影响和修正[J]. 地球物理学报, 2005, 48(5): 1 045-1 052 (Wang Min, Shen Zhengkang, Dong Danan. Effects of Non-Tectonic Crustal Deformation on Continuous GPS Position Time Series and Correction to Them[J]. Chinese Journal of Geophysics, 2005, 48(5): 1 045-1 052)
(  0) 0) |
| [4] |
He X X, Hua Z H, Yu K G, et al. Accuracy Enhancement of GPS Time Series Using Principal Component Analysis and Block Spatial Filtering[J]. Advances in Space Research, 2015, 55(5): 1 316-1 327 DOI:10.1016/j.asr.2014.12.016
(  0) 0) |
| [5] |
李昭, 姜卫平, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4): 496-503 (Li Zhao, Jiang Weiping, Liu Hongfei, et al. Noise Model Establishment and Analysis of IGS Reference Station Coordinate Time Series Inside China[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 496-503)
(  0) 0) |
| [6] |
Kargoll B, Kermarrec G, Korte J, et al. Self-Tuning Robust Adjustment within Multivariate Regression Time Series Models with Vector-Autoregressive Random Errors[J]. Journal of Geodesy, 2020, 94(5): 1-26
(  0) 0) |
| [7] |
Engle R F. Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom[J]. Econometrica, 1982, 50(4): 987-1 008 DOI:10.2307/1912773
(  0) 0) |
| [8] |
Wu D C, Yan H M, Shen Y C. TSAnalyzer, A GNSS Time Series Analysis Software[J]. GPS Solutions, 2017, 21(3): 1 389-1 394 DOI:10.1007/s10291-017-0637-2
(  0) 0) |
| [9] |
Aknouche A, Guerbyenne H. Recursive Estimation of GARCH Models[J]. Communications in Statistics-Simulation and Computation, 2006, 35(4): 925-938 DOI:10.1080/03610910600880328
(  0) 0) |
| [10] |
He X, Bos M S, Montillet J P, et al. Investigation of the Noise Properties at Low Frequencies in Long GNSS Time Series[J]. Journal of Geodesy, 2019, 93(9): 1 271-1 282
(  0) 0) |
| [11] |
Amiri-Simkooei A R, Tiberius C C J M, Teunissen P J G. Assessment of Noise in GPS Coordinate Time Series: Methodology and Results[J]. Journal of Geophysical Research: Solid Earth, 2007, 112(B7)
(  0) 0) |
2. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2023, Vol. 43
2023, Vol. 43

