2. 中国地震局地震大地测量重点实验室,武汉市洪山侧路40号,430071;
3. 湖北省地震局,武汉市洪山侧路48号,430071
作为形变观测仪器的一种,摆式倾斜仪通常用来进行固体潮和地震的观测。目前应用较为广泛的倾斜仪有VS型和VP型垂直摆倾斜仪[1-2],这2种仪器的设计结构原理相似,换能器的机械部分均采用立式摆式结构,信号调理电路部分则是以运放为核心的模拟电路[3],使得电路中的噪声等干扰被不可避免地混入原始信号中。
针对地震仪器的轻量化问题,Bashilov等[4]提出了一种具有更高集成度的地震仪,将数据的转换及记录集中在一个单板系统上,数字化程度较高且功能较为灵活;Zhang等[5]提出的检波器信号处理电路,结合了模拟电路和数字电路,也显示出模拟电路内部噪声对信号的显著影响。而在数据降噪方面,尚雪义等[6]及黄艳林[7]提出的利用经验模态分解与奇异值分解联合处理地震数据的方法,可有效提取数据特征。本文在现有研究基础上提出一种应用于新型摆式倾斜仪的信号调理方法,以数字电路为基础,仅使用少量必要的模拟电路成分改进前置放大电路,将倾斜仪的信号获取和处理聚合在一个小型化的系统上。为减少原始信号中的环境噪声,应用直接数字频率合成器(DDS)[8]、经验模态分解(EMD)[9]及奇异值分解(SVD)[10]等技术进行信号的调理。
1 信号调理原理在地震仪器中,差分电容传感器的驱动方式通常为调制器的形式[11],即外侧两极板接入一对振幅大小相等、相位相反的周期性震荡波。正弦波和方波这2种震荡波均在倾斜仪的设计中有所应用[3],其中正弦波为单一频率成分的波形,而方波含有大量的谐波,因此使用正弦波来进行信号的调制更加稳定和经济。通过相位累加器对幅值寻址是直接数字频率合成器[8]生成正弦波的基本原理,频率控制输入令相位累加器开始累加工作,而相位数据与幅值在内存地址中有一一对应的关系,这些幅值数据通过模拟-数字转换器(DAC)转换为连续的模拟电压信号,再经由滤波处理得到特定频率的正弦波形:
| $ a(t)=\cos \left(\frac{2 \pi}{N} t+\varphi_0\right) $ | (1) |
式中,a(t)为输入相位信息寻址对应的幅值变量,t为时间变量,N为相位分频系数,φ0为初始相位。原始的地动信号经驱动函数波形调制后,得到信号函数:
| $ x(t)=b(t) s(t) \cos (\varphi(t)) $ | (2) |
式中,x(t)为调制信号函数,b(t)为幅度调制函数,s(t)为基带信号函数,φ(t)为频率调制函数中的相位函数。此时的信号成分包含高频载波分量、代表地形变的低频分量及噪声分量,要将有用信号提取出来,需要对信号进行解调。正弦波幅度解调包括相干解调和非相干解调,本文设计使用相干解调,原因是相干解调恢复的信号质量优于非相干解调。具体方法是令一路与载波相干、同频同相的正弦波与调制信号相乘,通过滤波后剔除高频信号,恢复基带信号。根据式(1)和式(2)可推得,理论上调制信号与载波相乘的结果为:
| $ \begin{gathered} x(t) \cos (\varphi(t))=\frac{1}{2} b(t)s(t)+ \\ \frac{1}{2} b(t) s(t) \cos (2 \varphi(t)) \end{gathered} $ | (3) |
实际上,得到的信号是一种本征模态函数(IMF)信号[12]。传统的做法是使用滤波器直接剔除设置频率以外的成分,得到保留少量频率成分的单一信号,然而简单的低通滤波效果并不理想,且存在一定相移。经验模态分解的目标则是分离各成分信号,输出各个本征模态函数信号,在将部分成分筛除后重构信号。EMD算法对整体数据进行计算,避免了传统数字滤波中的相位延迟,可为后续实验研究提供更多参考数据。于是式(3)可写为:
| $ X(t)=\sum\limits_{i=1}^M B_i(t) s_i(t)+\sum\limits_{i=1}^M C_i(t) $ | (4) |
式中,X(t)=x(t)cos(φ(t)),Bi(t)和Ci(t)分别为幅度调制的函数及高频成分。利用三次样条插值[9]计算信号的上下包络线:
| $ \left\{\begin{array}{l} y_1=a_{1 i}+b_{1 i} X+c_{1 i} X^2+d_{1 i} X^3 \\ y_2=a_{2 i}+b_{2 i} X+c_{2 i} X^2+d_{2 i} X^3 \end{array}\right. $ | (5) |
原信号减上下包络线平均值得到第1个本征模态函数信号,此时的平均包络线作为求解下一个本征模态函数的数据源。经过几次循环迭代过程,源数据将被分解为带有不同成分特征的函数集,其中函数中包含了载波信号和噪声信号。当噪声频率数倍于基带信号频率(如3倍)时,分解出的第1个函数信号为高频特征信号,且不会有混叠影响。选取非高频信号的函数集进行信号重构,得到同时包含倾斜信息和部分低频噪声的原始信号s(t),这个过程即为信号的完全解调和初步降噪过程。为避免EMD算法带来的混叠问题,进一步的降噪工作利用奇异值分解(SVD)算法来完成。
首先将一维数据变换为二维数据,利用相空间重构方法[10, 13]生成信号函数s(t)数据的汉克尔矩阵(Hankel matrix)S:
| $ \boldsymbol{S}=\left[\begin{array}{cccc} s_1 & s_2 & \cdots & s_n \\ s_2 & s_3 & \cdots & s_{n+1} \\ & \vdots & & \\ s_m & s_{m+1} & \cdots & s_M \end{array}\right] $ | (6) |
式中,S为m×n阶的矩阵,且满足M=m+n-1。将数据整合为二维数据后,再进行计算得到矩阵S的奇异值分解形式:
| $ \mathit{\boldsymbol{S}} = \mathit{\boldsymbol{U \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{V}}^{\rm{T}}} $ | (7) |
式中,U和V分别为m阶和n阶的标准化正交矩阵,Σ为由矩阵S奇异值组成的m×n阶对角矩阵。U和V通过SST和STS的一系列计算得到,奇异值由非零特征值开平方得到。在矩阵Σ中的奇异值按照由大到小的顺序排列,且个数等于矩阵S的秩,奇异值的排列顺序代表对信号主成分的权重,而随机噪声显然对信号主体构成的权重小。为去除信号中的噪声,仅保留矩阵Σ中的部分奇异值,其他奇异值全部置零(实际上位于后半段的奇异值远小于靠前位置的奇异值)。经过迭代等计算后执行奇异值分解的逆过程重构信号,此时得到降噪后较为纯净的信号s′(t)。
经过以上处理获取的数据信号,实际上是差分电容中间极板的电压值,即x(t)=US(t)。根据差分电容的特性,传感器输出电压,即输入到调理电路进行类型转换的信号函数为[2]:
| $ U_S(t)=\frac{L_S(t)}{L_0} U_C(t) $ | (8) |
式中,US(t为电容传感器输出电压,LS(t为传感器测得的中间极板相对于中间位置的位移,L0为电容中间极板处于中间位置时与两侧极板间距(即静止位置),UC(t为驱动电压即载波。由式(2)可得,倾斜量与摆体输出之间的关系为:
| $ L_S(t)=\frac{L_0 U_S(t)}{b(t) \cos \left(2 \pi f_c t\right)} $ | (9) |
| $ L_S(t)=s^{\prime}(t) L_0 $ | (10) |
式中,fc为驱动正弦波频率。式(9)与式(10)分别为摆体倾斜量与电压之间的关系及倾斜量与解调降噪后信号函数的关系,因此处理后的信号可直接体现摆体的状态。
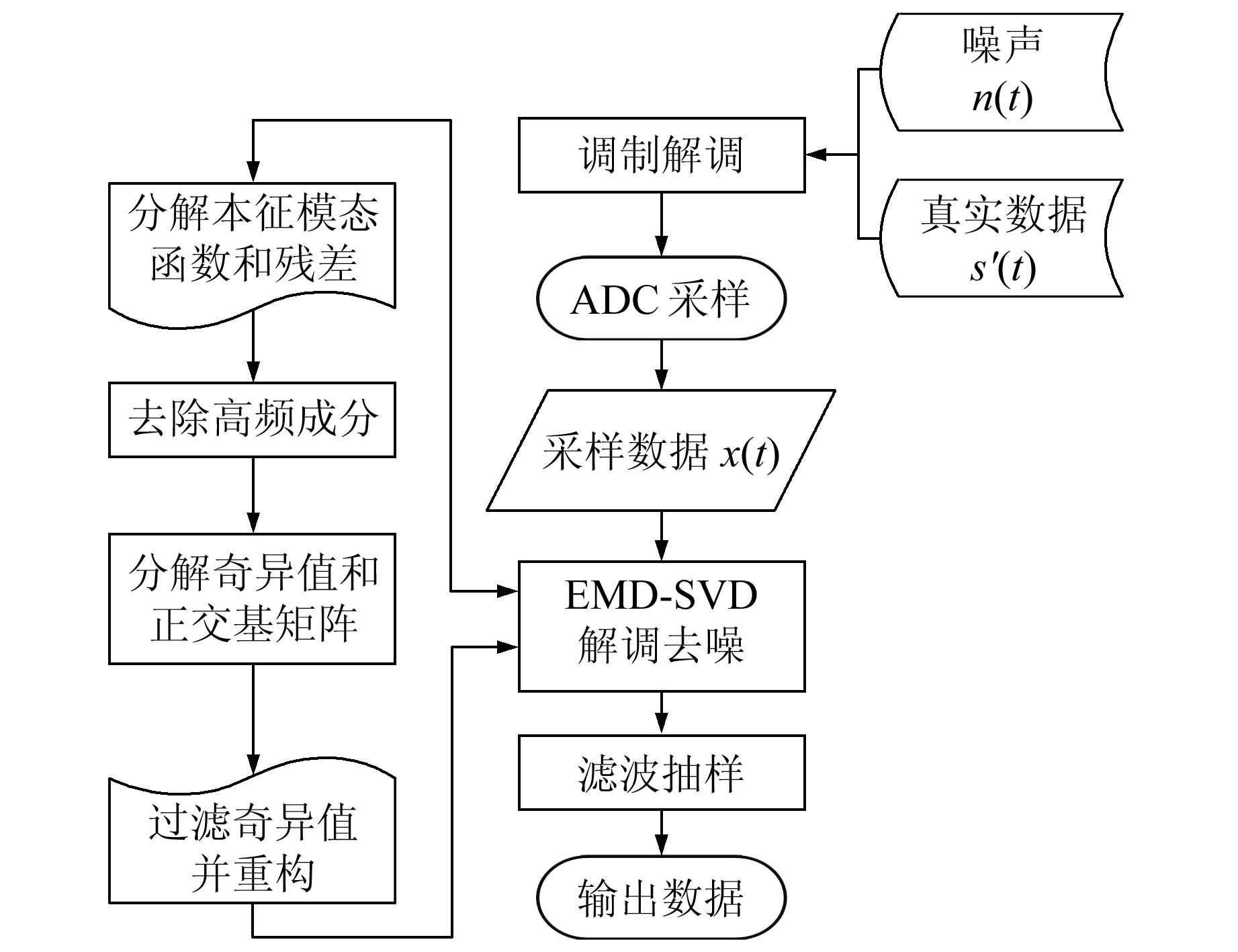
信号调理的过程原理如图 1所示。由于省去了部分前级放大和滤波等过程,原始基带信号会不可避免地掺杂一定程度的噪声,其中包括周期性的规律噪声和非线性的无规律噪声。在信号处理过程中得到丰富且纯净的信号是整个电路设计的首要目标,因此数据处理算法在实际电路中的实现较为重要。EMD算法对去除高频噪声有显著效果,而SVD算法更加适合处理随机噪声。因此,本文将2种算法相结合,可满足含有不同类型噪声信号的处理需求。
|
图 1 信号调理和处理工作原理 Fig. 1 Principle of signal conditioning and processing |
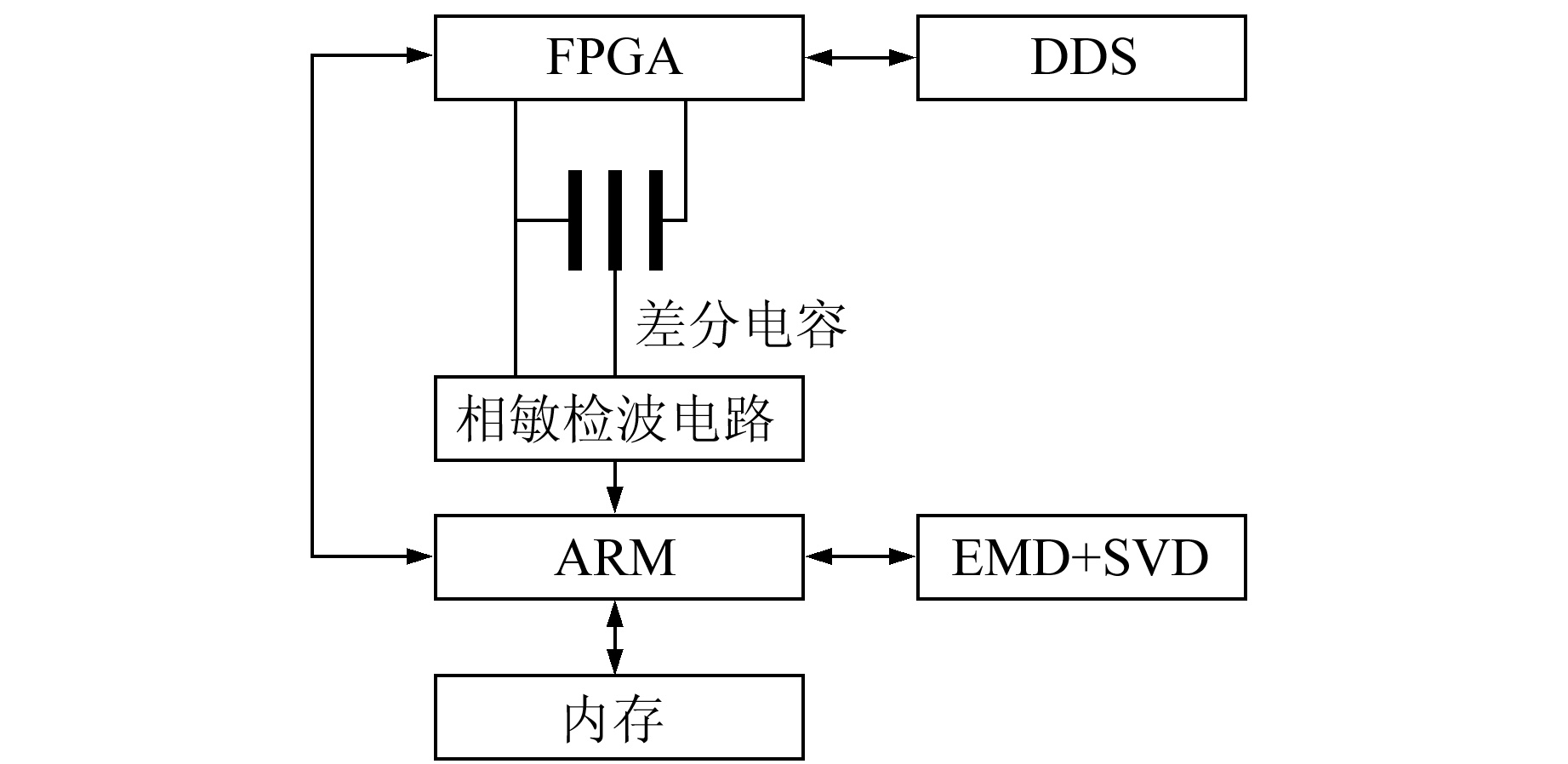
电路总体设计分为信号获取和信号处理两部分,信号的获取部分以模拟电路为主,处理部分以数字电路为主。将以往摆和数采分离的形式改为传感器和信号处理系统一体化的设计,利用数字化的设计舍弃一部分模拟电路,电路设计原理如图 2所示。驱动传感器的激励电压由FPGA电路生成,逻辑核查找表(LUT)数据输出接口连接到数-模转换电器,生成一个频率、深度和位宽可编程控制的波形(DDS)。其信号频率为:
| $ f_{\mathrm{cos}}=f_{\mathrm{clk}} \frac{m}{2^N} $ | (11) |
|
图 2 电路设计原理 Fig. 2 Principle of circuit design |
式中,fclk为系统时钟频率,fcos为输出正弦信号频率,m为每次进行相位累加的相位增量,N为相位信息序列位宽。由传感器引出的调制信号经过相敏检波电路进行解调,相敏检波电路主要由运算放大器和乘法器构成,实现信号的初步解调和滤波。为压制信号中的噪声,也为方便信号的采集,设计了基于ARM微处理器的软件滤波系统。在进行去噪处理前,首先将信号转换为数字信号并将数据存储到内存中,然后利用EMD算法和SVD算法对数据进行处理。在程序设计中,为保证系统的稳定性,预先占用地址生成矩阵,为尽可能保留更多的数据信息,仅去除最高频的模态分量,同时为更好地压制噪声,仅保留前10%的奇异值。
为测试降噪算法的性能,生成一组多频率成分的信号,并加入随机噪声,使用本文算法程序进行处理。图 3为信号调理测试过程和结果,其中原始信号由0.1~100 Hz不同频率的正弦波组成。为模拟实际观测信号并检验模型,在原始信号中加入信噪比为0.1 dB的高斯噪声,可以看出,加入随机噪声后信号特征被显著干扰,基本被湮没在噪声中。经过调制解调和去噪后,信号特征被恢复出来,且信噪比可达15 dB,因未使用常规窗函数等滤波器,重构出来的信号未出现明显相移和失真。恢复出的信号有一些细节没有被完整保留,原因是加入的高斯白噪声干扰过强,且数据处理系统对高频信号关注度不高。经过低通滤波后可得到较为纯净的低频采集数据,此时再对获取的数据进行抽样或滤波等操作,成本不高且信号质量也可得到明显改善。

|
图 3 算法测试结果 Fig. 3 Algorithm test results |
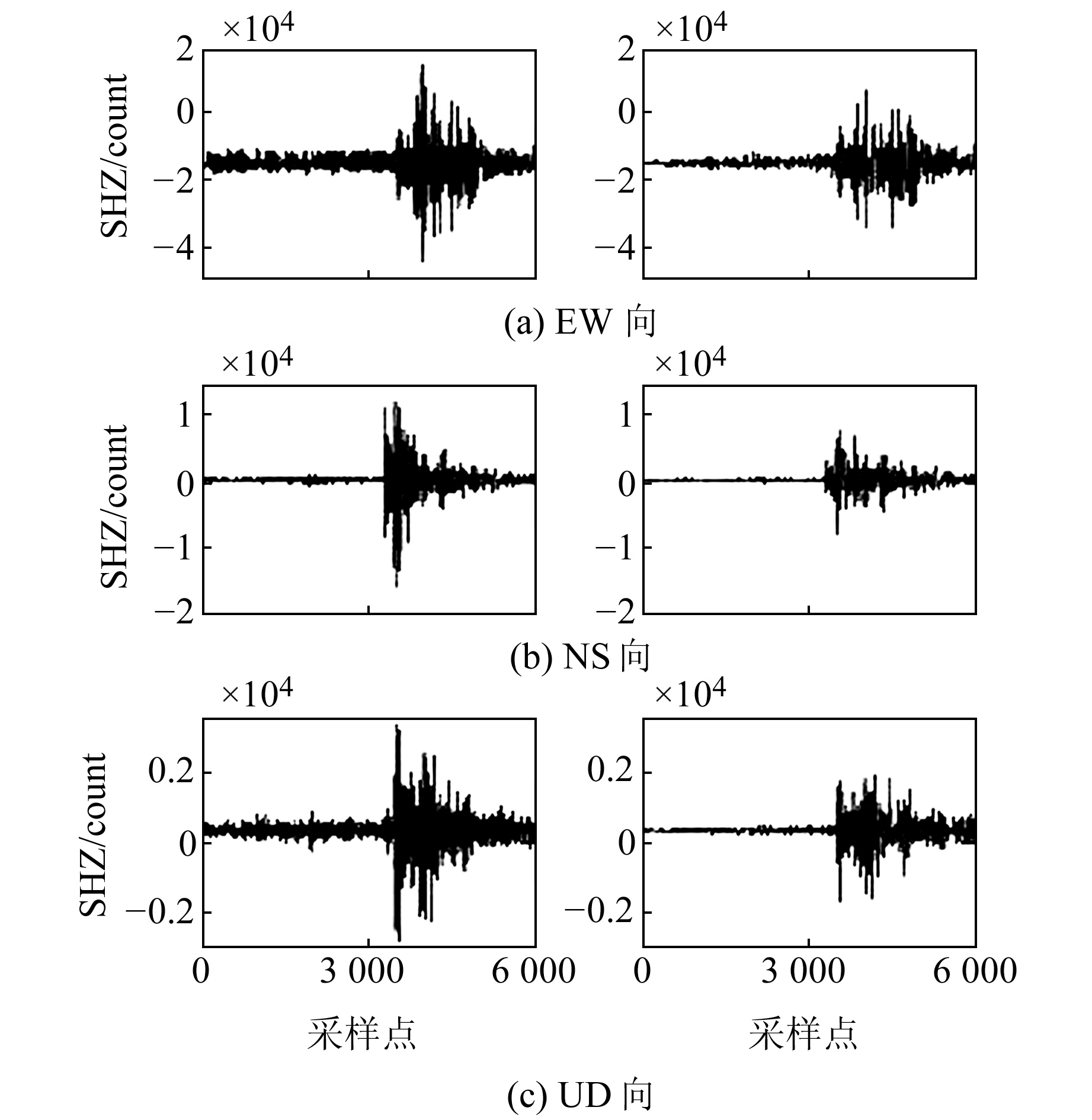
为了对降噪算法处理地震数据的性能进行实验验证,随机选取2组地震数据进行降噪处理。本文选取2016-03-27宾川地震台记录的地震事件数据,首先截取P波到达时刻前后30 s的6 000个数据点。图 4左侧为地震计原始数据,右侧为使用本文降噪算法处理地震数据的结果,可以看出,经处理后数据噪声水平明显下降,无地震时段的数据平稳度明显提高,数据质量得到了有效改善。实验证明:使用本文设计的算法进行信号处理可得到更高质量的数据。
|
图 4 台网P波初至段数据降噪结果 Fig. 4 Denoising results of P-arrival data |
目前,地震台站中安装运行的摆式倾斜仪在信号调理设计中无降噪算法。为检验本文算法对倾斜仪固体潮观测的降噪效果,选取现有3组含有明显噪声或较强干扰但不含地震波的摆式倾斜仪数据进行处理。图 5为3组原始数据及其处理结果,可以看到,存在异常的短暂大幅值干扰信号经过处理后其畸变附近信号质量明显改善,已被恢复为前后连续的较为平滑的状态。为不丢失真实的地震动信息,对高频信息的去除程度不宜过强,这也是图 5中恢复后信号不完全平滑的原因。由既得数据经本文算法处理结果可以推断,将EMD-SVD算法应用到信号调理电路系统中,可有效提高信噪比,改善信号的平滑程度,同时减弱数据短时出现异常带来的影响。

|
图 5 台网倾斜仪数据及处理结果 Fig. 5 Data and processing results of tiltmeter |
电路实验使用的数字处理平台为Xilinx生产的FPGA电路芯片,搭建的放大电路等模拟电路部分选取的是由ADI公司生产的运放等电路芯片。整个电路调理设计由硬件调理和软件调理交叉组成,各阶段工作过程由软硬件交替完成。设置摆以1 Hz频率摆动,输出数据设置为10点/s,不定时地随机进行运行实验。传感器的震动频率为1 Hz,选取几秒钟数据即可观测到几段完整周期,图 6为新型摆式倾斜仪信号调理电路中6组实验结果。

|
图 6 实验输出结果 Fig. 6 Results of experiment output |
为对系统进行进一步升级优化,设计中涉及的电路板和线路等部分暴露在空气中,会不可避免地受到较强的干扰。然而,根据现有数据结果可以判断信号调理的效果,即在一定程度上恢复传感器周期摆动时电压变化的特征。ADC采样的时间点是随机选取的,因此图 6中6组数据的初相不同。由于传感器是固定频率的规律性摆动,在数据段内显示出了周期数的完整性。尽管在输出数据中出现了几处局部前后变化不完全平滑的数据点,但总体上呈现出完整且清晰的周期性波动。这表示本文设计的信号调理电路在强干扰、高噪声水平条件下,能较好地恢复传感器电压变化状态,证明本文信号调理方法具有可行性,不仅电路集成度高、处理过程灵活,还具备较好的稳定性和可靠性,在改进摆式倾斜仪信号电路调理上有很好的应用价值。
4 结语本文提出了一种应用在新型摆式倾斜仪上的信号调理方法,并针对信号处理方法的核心技术进行了测试和数据实验。通过少量的模拟电路设计和大量的数字电路设计,使数据处理系统更加数字化和集成化。利用数字滤波和降噪等信号处理方法,避免了传统电路中出现相移或电路干扰等问题;利用嵌入式芯片,将EMD-SVD降噪算法应用到倾斜仪的信号调理中,以FPGA为核心的信号调理电路,可降低信号采集的成本,提高数据处理效果;以数字系统为核心意味着整个信号处理过程多处可自由控制,包括可编程控制的传感器驱动电压参数和滤波降噪参数。由测试和数据实验结果可知,本文提出的滤波和降噪方法对剔除调理过程中出现的干扰信号效果显著,电路设计具有集成度高、低频扰动处的适应性强、处置偶发异常数据性能好等特点,且具有一定的提升空间。
| [1] |
Furst S, Chéry J, Mohammadi B, et al. Joint Estimation of Tiltmeter Drift and Volume Variation during Reservoir Monitoring[J]. Journal of Geodesy, 2019, 93(8): 1 137-1 146 DOI:10.1007/s00190-019-01231-3
(  0) 0) |
| [2] |
肖峻. 高精度垂直摆倾斜仪及其应用研究[D]. 武汉: 中国科学院测量与地球物理研究所, 2002 (Xiao Jun. High Precision Vertical Pendulum Tiltmeter and Its Application[D]. Wuhan: Institute of Geodesy and Geophysics, CAS, 2002)
(  0) 0) |
| [3] |
Ma W G, Wu Y X, Zhao H Q. Comparison of VP Broadband Tiltmeter and VS Vertical Pendulum Tiltmeter[J]. Geodesy and Geodynamics, 2015, 6(3): 226-232 DOI:10.1016/j.geog.2015.02.002
(  0) 0) |
| [4] |
Bashilov I P, Volosov S G, Zubko Y N, et al. Portable Digital Seismometer[J]. Seismic Instruments, 2011, 47(1): 80-88 DOI:10.3103/S074792391101004X
(  0) 0) |
| [5] |
Zhang X P, Wei X Y, Wang T D, et al. A Digital Low-Frequency Geophone Based on 4th-Order Sigma-Delta Modulator and Single-Coil Velocity Feedback[J]. Sensors and Actuators A: Physical, 2020, 312: 112074 DOI:10.1016/j.sna.2020.112074
(  0) 0) |
| [6] |
尚雪义, 李夕兵, 彭康, 等. 基于EMDSVD的矿山微震与爆破信号特征提取及分类方法[J]. 岩土工程学报, 2016, 38(10): 1 849-1 858 (Shang Xueyi, Li Xibing, Peng Kang, et al. Feature Extraction and Classification of Mine Microseism and Blast Based on EMD-SVD[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(10): 1 849-1 858)
(  0) 0) |
| [7] |
黄艳林. SVD与EMD联合去噪方法在地震勘探数据处理中的研究与应用[J]. 地震工程学报, 2016, 38(2): 323-326 (Huang Yanlin. Application of Joint Denoising Using Empirical Mode Decomposition and Singular Value Decomposition in Seismic Data Processing[J]. China Earthquake Engineering Journal, 2016, 38(2): 323-326 DOI:10.3969/j.issn.1000-0844.2016.02.0323)
(  0) 0) |
| [8] |
Tierney J, Rader C, Gold B. A Digital Frequency Synthesizer[J]. IEEE Transactions on Audio and Electroacoustics, 1971, 19(1): 48-57 DOI:10.1109/TAU.1971.1162151
(  0) 0) |
| [9] |
Wu Z H, Huang N E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41 DOI:10.1142/S1793536909000047
(  0) 0) |
| [10] |
Zhang G, Xu B B, Zhang K S, et al. Research on a Noise Reduction Method Based on Multi-Resolution Singular Value Decomposition[J]. Applied Sciences, 2020, 10(4): 1 409 DOI:10.3390/app10041409
(  0) 0) |
| [11] |
Amini A, Trifunac M. Analysis of a Force Balance Accelerometer[J]. International Journal of Soil Dynamics and Earthquake Engineering, 1985, 4(2): 82-90 DOI:10.1016/0261-7277(85)90003-8
(  0) 0) |
| [12] |
Hu X Y, Peng S L, Hwang W L. EMD Revisited: A New Understanding of the Envelope and Resolving the Mode-Mixing Problem in AM-FM Signals[J]. IEEE Transactions on Signal Processing, 2012, 60(3): 1 075-1 086 DOI:10.1109/TSP.2011.2179650
(  0) 0) |
| [13] |
Chen M C, He Y X. Wire Rope Weak Defect Signal Processing Methods Based on Improved SVD and Phase Space Reconstruction[J]. Information Technology and Control, 2021, 50(4): 752-768 DOI:10.5755/j01.itc.50.4.28105
(  0) 0) |
2. Key Laboratory of Earthquake Geodesy, CEA, 40 Hongshance Road, Wuhan 430071, China;
3. Hubei Earthquake Agency, 48 Hongshance Road, Wuhan 430071, China
 2023, Vol. 43
2023, Vol. 43


