2. 湖北工业大学土木建筑与环境学院,武汉市南李路28号,430068
大幅值的竖向地震动是强震事件地面运动的显著特征。自1971年San Fernando M6.6地震报道了1 200 Gal的竖向地震动加速度之后,1995年日本阪神M7.2地震、2008年汶川M8.0地震、2021年青海玛多M7.4地震中均观测到竖向地震动对于建筑、桥梁及地铁等结构的显著破坏[1-2]。当前竖向地震动的研究重点关注其与水平向地震动之间的比例关系,在工程应用上则通常选择水平向地震动参数的2/3作为竖向地震动进行输入。然而,由于地震事件的复杂性及强震观测资料的不足,竖向地震动的拟合通常存在较大残差从而导致较大的不确定性。实际的强震观测记录表明,近断层地区竖向地震动与水平向地震动参数的比值可以达到3.77[3],这可能会造成框架或框剪结构的内部框架柱在竖向地震动作用下承受反复的压缩或剪压破坏作用[4-5]。
有学者尝试使用人工智能的相关方法解决地震工程学竖向地震动参数估计的不确定性问题,如模拟退火算法-人工神经网络(SA-ANN)的地震动预测模型及基于最小二乘-遗传规划(GP-OLS)的地震动预测模型[6]。本文在此基础之上,提出一种基于自适应神经模糊推理系统(adaptive neuro fuzzy inference system,ANFIS) 的竖向地震动参数预测模型,并给出其结果分析和信度检验,为地震危险性分析、地震地质灾害评价及建筑结构抗震设防等提供简单可靠的竖向地震动参数。
1 自适应神经模糊推理系统ANFIS是一种以人工智能方法为理论基础的推理模型,使用传统的神经网络方法来实现,主要包括模糊化、模糊推理和反模糊化3个基本步骤[7]。模糊推理的if-then规则如下:
| $ \begin{array}{l} 规则1:{\rm{if}}\ {x_{\rm{1}}}\ {\rm{is}}\ {A_{\rm{1}}}\ {\rm{and\ if}}\ {x_{\rm{2}}}\ {\rm{is}}\ {B_{\rm{1}}}\\ \ \ \ \ \ \ \ \ {\rm{then }}\ {f_1} = {p_1}{x_1} + {q_1}{x_2} + {r_1} \end{array} $ | (1) |
| $ \begin{array}{l} 规则2:{\rm{if}}\ {x_{\rm{1}}}\ {\rm{is}}\ {A_{\rm{2}}}\ {\rm{and\ if}}\ {x_{\rm{2}}}\ {\rm{is}}\ {B_{\rm{2}}}\\ \ \ \ \ \ \ \ \ {\rm{then }}\ {f_2} = {p_2}{x_1} + {q_2}{x_2} + {r_2} \end{array} $ | (2) |
ANFIS可以认为是T-S型模糊控制的神经网络的实现,该网络是一个多层前馈网络,其结构如图 1所示。

|
图 1 ANFIS结构 Fig. 1 Structure of ANFIS |
第1层输入变量模糊化,该层参数可变,每个节点以节点函数表示:
| $ O_{1, i}=\mu_{A i}\left(x_1\right), i=1, 2 $ | (3) |
| $ O_{1, i}=\mu_{B(i-2)}\left(x_2\right), i=3, 4 $ | (4) |
式中,x1、x2为节点的输入,O1, i为模糊集Ai的隶属函数,隶属函数的参数集为前提参数。
第2层进行模糊集运算,输入信号相乘,将其乘积输出为:
| $ O_{2, i}=\omega_i=\mu_{A i}\left(x_1\right) \mu_{B i}\left(x_2\right), i=1, 2 $ | (5) |
第3层计算每条规则ωi与全部规则之和ω的比值:
| $ O_{3, i}=\bar{\omega}_i=\frac{\omega_i}{\omega_1+\omega_2}, i=1, 2 $ | (6) |
第4层计算每条规则输出:
| $ O_{4, i}=\bar{\omega}_i f_i=\bar{\omega}_i\left(p_i x_1+q_i x_2+r_i\right), i=1, 2 $ | (7) |
式中,{pi, qi, ri}为结论参数。
第5层计算所有输入信号的总输出:
| $ O_{5, i}=\sum\limits_i \bar{\omega}_i f_i, i=1, 2 $ | (8) |
由于PEER NGA强震数据库记录时均采用带通滤波处理,对加速度和速度的影响较小,而对位移的影响大,因此本文选择竖向地震动峰值加速度PGA及峰值速度PGV作为模型的预测目标参数。模型输入变量为震级、场地条件和断层距,暂不考虑强地面运动过程中的破裂长度、破裂方向、应力降等震源物理力学参数。
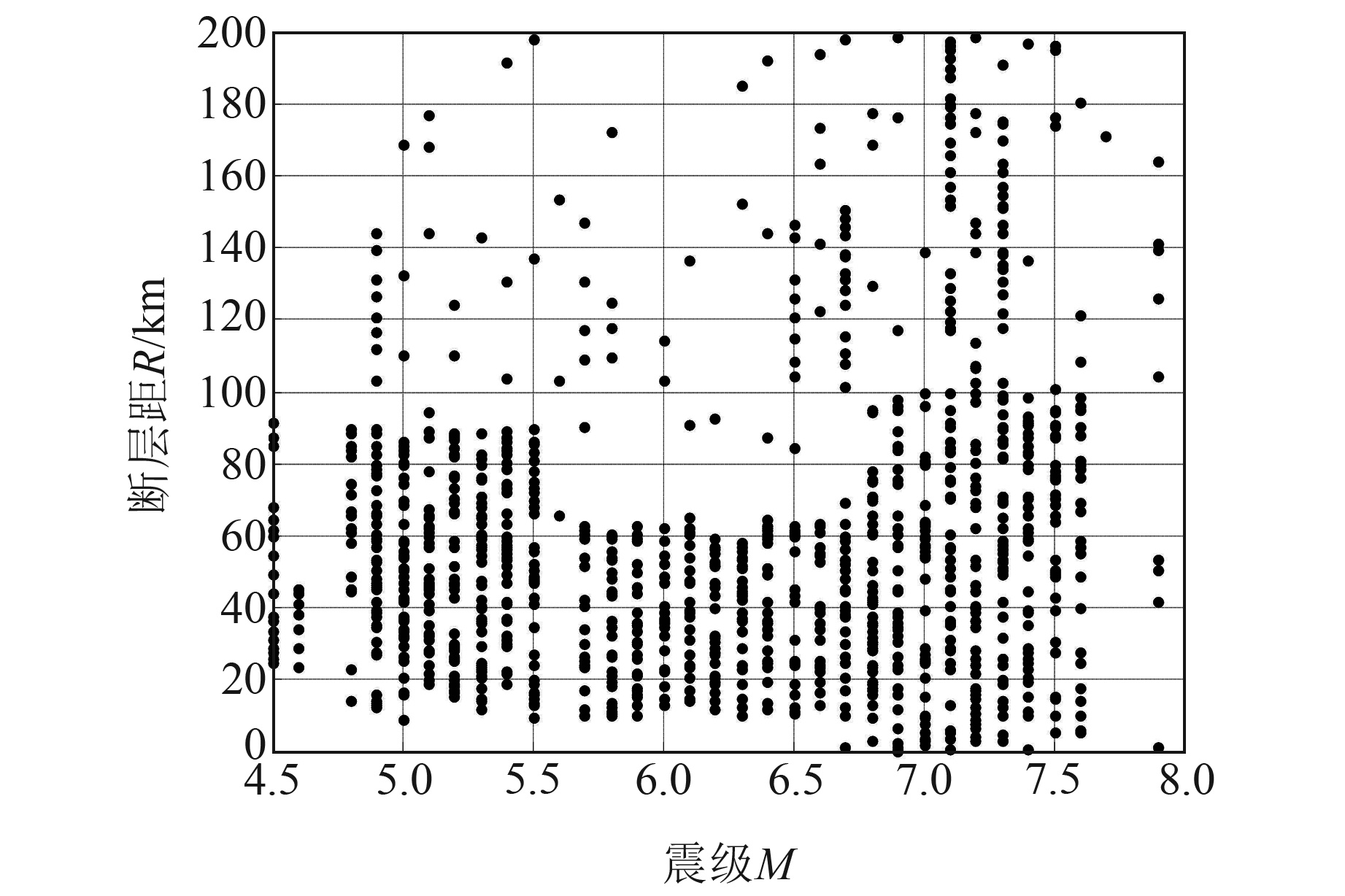
2.1 强地面运动波形数据选择PEER NGA数据库中AS08数据集的652条竖向地震动观测波形进行模型构建,地震加速度波形记录来自于135次地震事件,其中主震94次,余震41次[3]。图 2给出数据集震级和断层距的分布情况,表 1给出所使用地震观测波形的总体情况,使用参数最大值、最小值、平均值和标准差来反映数据的统计性质。
|
图 2 AS08数据集的震级和断层距 Fig. 2 Magnitude and fault distance of AS08 dataset |
|
|
表 1 AS08数据集地震波形的总体情况 Tab. 1 Overview of seismic waveforms of AS08 dataset |
本文的目标在于给出一个地震动参数的预测方程,具体为:
| $ \ln (Y)=f(M, V, \ln (R)) $ | (9) |
式中,Y为竖向地震动峰值加速度PGA及峰值速度PGV,M为震级,V为观测场30 m以内的平均剪切波速,R为断层距。
选择地震震级、震源机制类型、平均剪切波速和断层距作为输入属性,并将竖向地震动参数PGA及PGV作为模型的输出参数Y,以此对PGA及PGV分别建立模型。将数据分为2个部分,即训练数据集和检验数据集,两者比例为3 ∶1,即训练集波形489条,检验数据集数163条。
首先对数据集进行标准化处理,假设Z为拟进行标准化的变量,Zmax和Zmin分别代表Z的最大和最小值。令标准化区间为[P, Q],本文取[0.05,0.95],令Zn为标准值,使用下式进行标准化处理:
| $ Z_n=c Z+d $ | (10) |
| $ c=(Q-P) /\left(Z_{\max }-Z_{\min }\right) $ | (11) |
| $ d=Q-c Z_{\max } $ | (12) |
进一步采用广义钟形隶属度函数确定每个输入变量的隶属度,包括a、b、c三个拟合参数,输出隶属度函数采用线性函数[8]:
| $ \operatorname{gbell}(x ; a, b, c)=\frac{1}{1+\left|\frac{x-c}{a}\right|^{2 b}} $ | (13) |
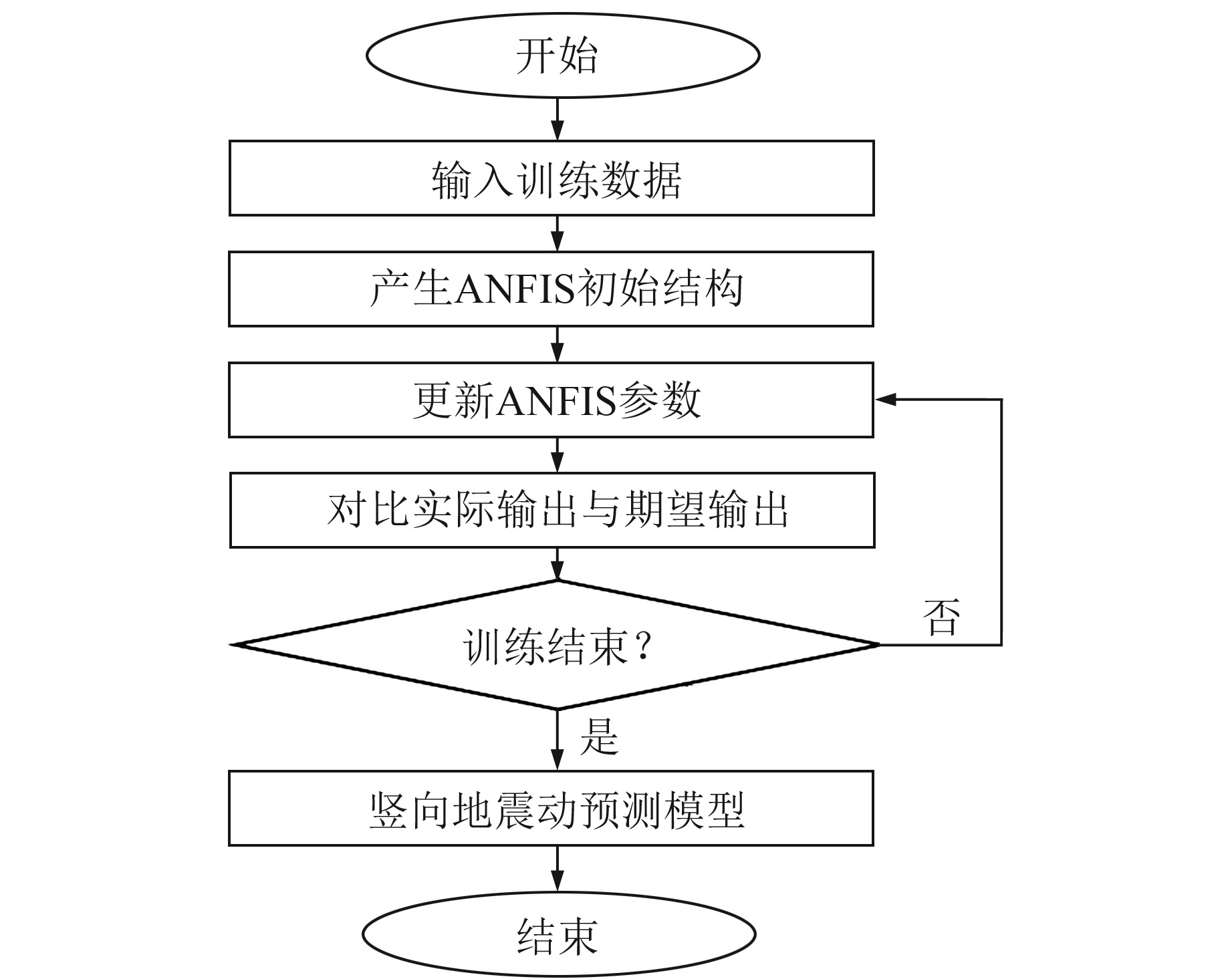
将ANFIS系统采用的学习方法指定为梯度下降反向传递法与最小二乘法的混合算法,训练迭代次数为100。图 3为更为细致的建模流程。
|
图 3 ANFIS竖向地震动预测模型建模流程 Fig. 3 Modeling process of ANFIS vertical ground motionprediction model |
图 4为训练数据集下ANFIS系统的学习过程。可见,随着迭代次数的不断增加,竖向PGA和PGV预测结果的平均绝对百分比误差分别逐步降低至0.156和0.162左右,说明ANFIS模型已经收敛,其前提参数见表 2,从而获得ANFIS竖向地震动参数预测模型。

|
图 4 ANFIS系统学习过程 Fig. 4 Learning process of ANFIS system |
|
|
表 2 ANFIS竖向地震动预测模型的前提参数 Tab. 2 Prerequisite parameters of ANFIS vertical ground motion prediction model |
使用相关系数R、平均绝对误差MAE、平均绝对百分比误差MAPE及均方根误差RMSE检验预测模型的效果:
| $ R=\frac{\sum\limits_{i=1}^k\left(\operatorname{obs}_i-\operatorname{avg}\left(\mathrm{obs}_i\right)\right)\left(\operatorname{pred}_i-\operatorname{avg}\left(\operatorname{pred} d_i\right)\right)}{\sqrt{\sum\limits_{i=1}^k\left(\operatorname{obs}_i-\operatorname{avg}\left(\operatorname{obs}_i\right)\right)^2 \sum\limits_{i=1}^k\left(\operatorname{pred}_i-\operatorname{avg}\left(\operatorname{pred}_i\right)\right)^2}} $ | (14) |
| $ \mathrm{MAE}=\sum\limits_{i=1}^k\left|\mathrm{obs}_i-\operatorname{pred}_i\right| / k $ | (15) |
| $ \mathrm{MAPE}=\sum\limits_{i=1}^k\left|\left(\mathrm{obs}_i-\operatorname{pred}_i\right) / \mathrm{obs}_i\right| / k $ | (16) |
| $ \operatorname{RMSE}=\sqrt{\sum\limits_{i=1}^k\left(\mathrm{obs}_i-\operatorname{pred}_i\right)^2 / k} $ | (17) |
式中,k、obsi、predi、avg(obsi)、avg(predi)分别代表地震记录的总数、观测值、预测值、观测值的平均值和预测值的平均值。
3.2 信度检验首先分析ANFIS竖向地震动参数预测模型在训练集和测试集下的误差情况;然后对比其与ANN-SA及GP-OLS两种机器学习类地震预测模型的预测效能;最后,利用MAPE指标,对比其与地震动衰减关系类地震动参数预测模型的预测效能。
表 3给出了AS08数据训练集和测试集的误差分析结果,图 5给出了训练集与测试集下竖向PGA和PGV的预测值与观测值拟合情况。
|
|
表 3 ANFIS竖向地震动预测模型的误差分析 Tab. 3 Error analysis of ANFIS vertical ground motion prediction model |
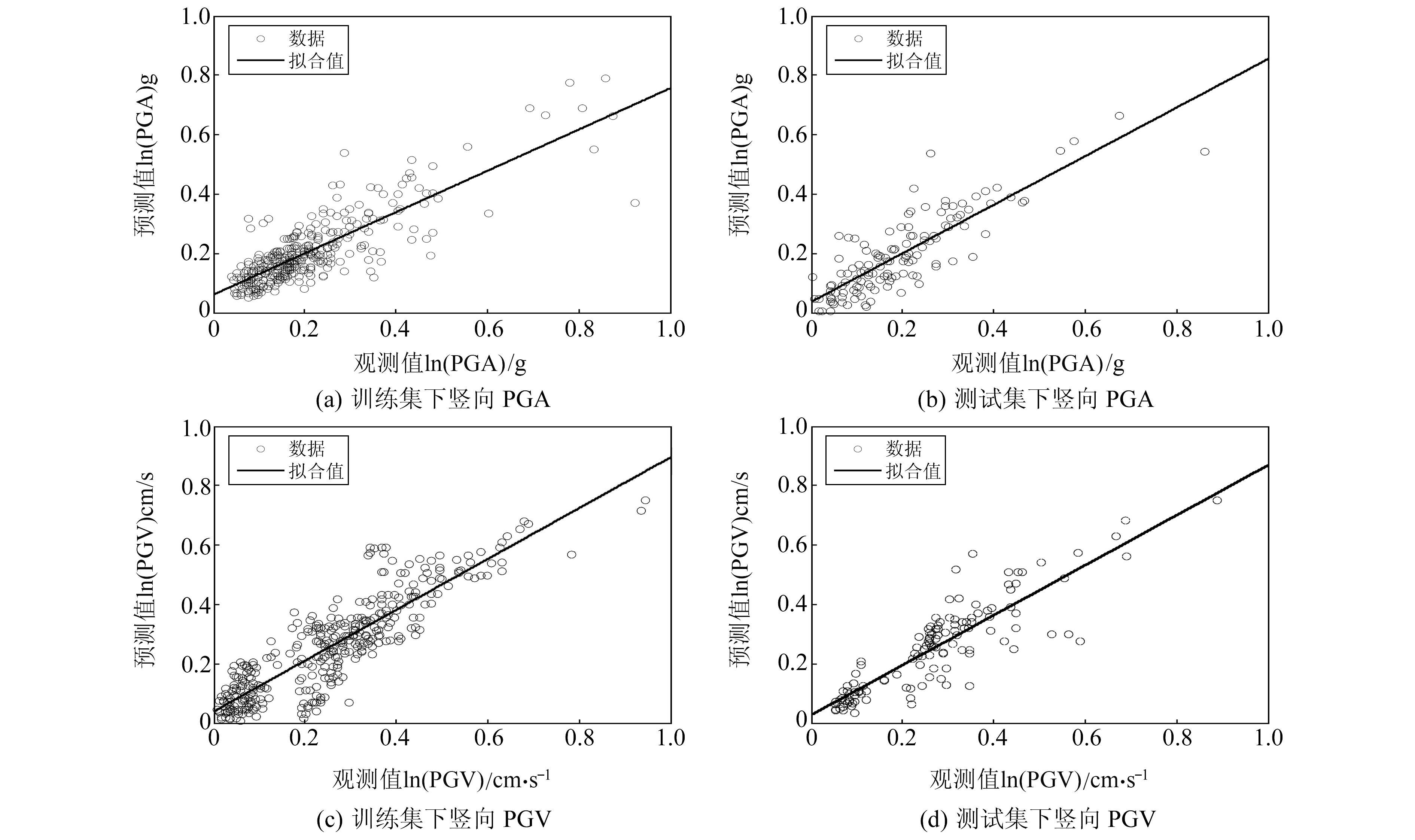
|
图 5 预测值和观测值拟合情况 Fig. 5 Predicted and observed values of vertical PGV under test set |
结合图 5(a)、5(b)和表 3可见,训练集与测试集下PGA的预测值与观测值具有良好的相关性,R分别为0.832和0.818;MAE分别约为0.013和0.024;MAPE分别约为0.133和0.156;RMSE分别为0.021和0.042。可以发现,训练集下的相关系数R大于测试集,且训练集下的误差指标MAE、MAPE及RMSE均低于测试集,说明对PGA的预测效能而言,ANFIS模型对训练集的拟合效果更好。但是考虑到测试集的相关系数R>0.8,且3类误差指标均处于较低水平,预测值与观测结果在图 5(b)所呈现的高相关性特征说明本文提出的竖向地震动PGA预测模型具备较好的泛化能力。
结合图 5(c)、5(d)和表 3可见,训练集与测试集下PGV的预测值与观测值亦具有良好的相关性,R分别为0.875和0.843;MAE分别约为0.011和0.023;MAPE分别约为0.123和0.153;RMSE分别为0.027和0.035。可以发现,与PGA模型一样,其R同样呈现出训练集大于测试集且误差指标MAE、MAPE及RMSE均低于测试集的特征。PGV模型的拟合精度略优于PGA模型,亦具有有效的泛化推理能力。
表 4为3个机器学习类模型的误差对比情况,可以看出,ANFIS模型预测结果精度更高。但需要指出的是,ANFIS竖向地震动参数预测模型的R略小于ANN-SA和GP-OLS模型,其原因可能在于所使用的竖向地震波形相对较少,导致观测值与预测值之间的相关性减弱。
|
|
表 4 不同机器学习预测模型的误差对比 Tab. 4 Error comparison of different machine learning prediction models |
由于当前没有公开发表的竖向地震动参数衰减关系模型,本文进一步选用水平向地震动衰减关系模型Campbel-Bozorgnia[3]进行对比(表 5)。可以看出,与水平向地震动衰减关系模型相比,ANFIS竖向地震动模型PGA预测的准确率提升约77.4%,PGV预测的准确率提升约62.7%。值得指出的是,本文仅使用PEER NGA数据库中包含652条波形的AS08数据集,与Campbell-Bozorgnia衰减关系使用的NGA数据库不完全相同,但与后者相比,本文模型仅需输入3个地球物理学参数,具有更好的工程易用性。
|
|
表 5 ANFIS竖向地震动参数预测模型与地震动衰减关系的误差对比 Tab. 5 Error comparison between ANFIS vertical ground motion prediction model and ground motion attenuation |
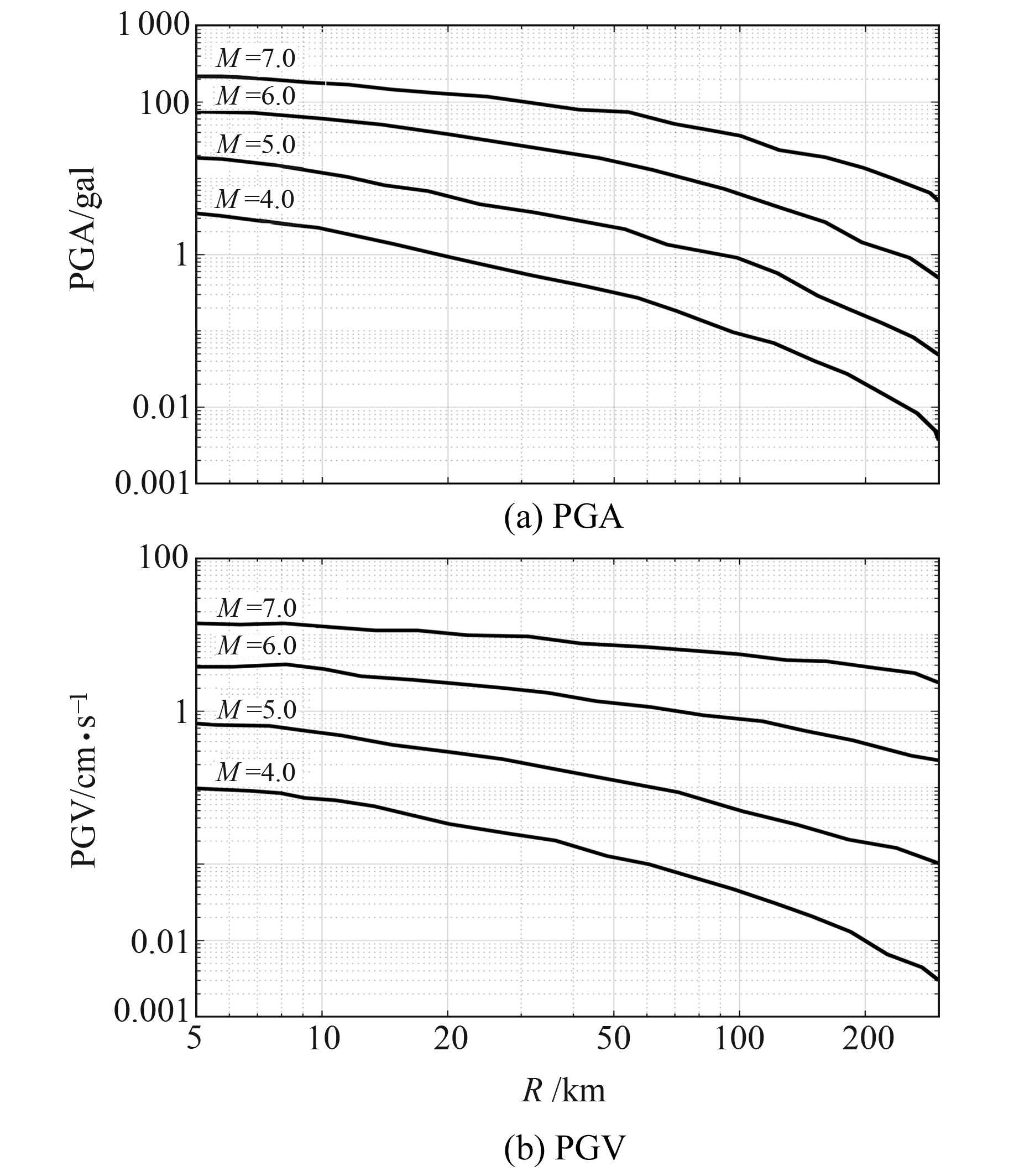
对ANFIS竖向地震动参数预测模型的计算结果进行分析。按照地震工程的实际,给出基岩场地(VS=760 m/s)条件下竖向地震动PGA及PGV随震级M和断层距R的变化情况(图 6)。
|
图 6 基岩场地条件下的竖向地震动衰减 Fig. 6 Attenuation of vertical ground motion under the condition of bedrock |
图 6中曲线分别代表ANFIS竖向地震动参数预测模型在M=4.0、5.0、6.0和7.0时的地震动衰减特征,可以看出,近断层区域内随着竖向地震动PGA及PGV的增大,震级的增大呈现出大震近场震级饱和的特征;但随着震级的增大和断层距的减小,PGA和PGV的增大放缓,并未出现明显的过饱和现象。
同时可见,断层距R<10 km距离范围内,4个震级的竖向PGA及PGV衰减曲线的斜率大致相同;而10 km≤R≤300 km距离范围内,随着断层距增大,PGA的衰减速度比PGV快,说明高频地震动的衰减比长周期分量显著。
为研究本文模型所获得竖向地震动参数的场地放大效应,以基岩场地(VS30=1 000 m/s)处的PGA和PGV为基准,计算不同VS30条件下的地震动放大系数,如图 7所示。
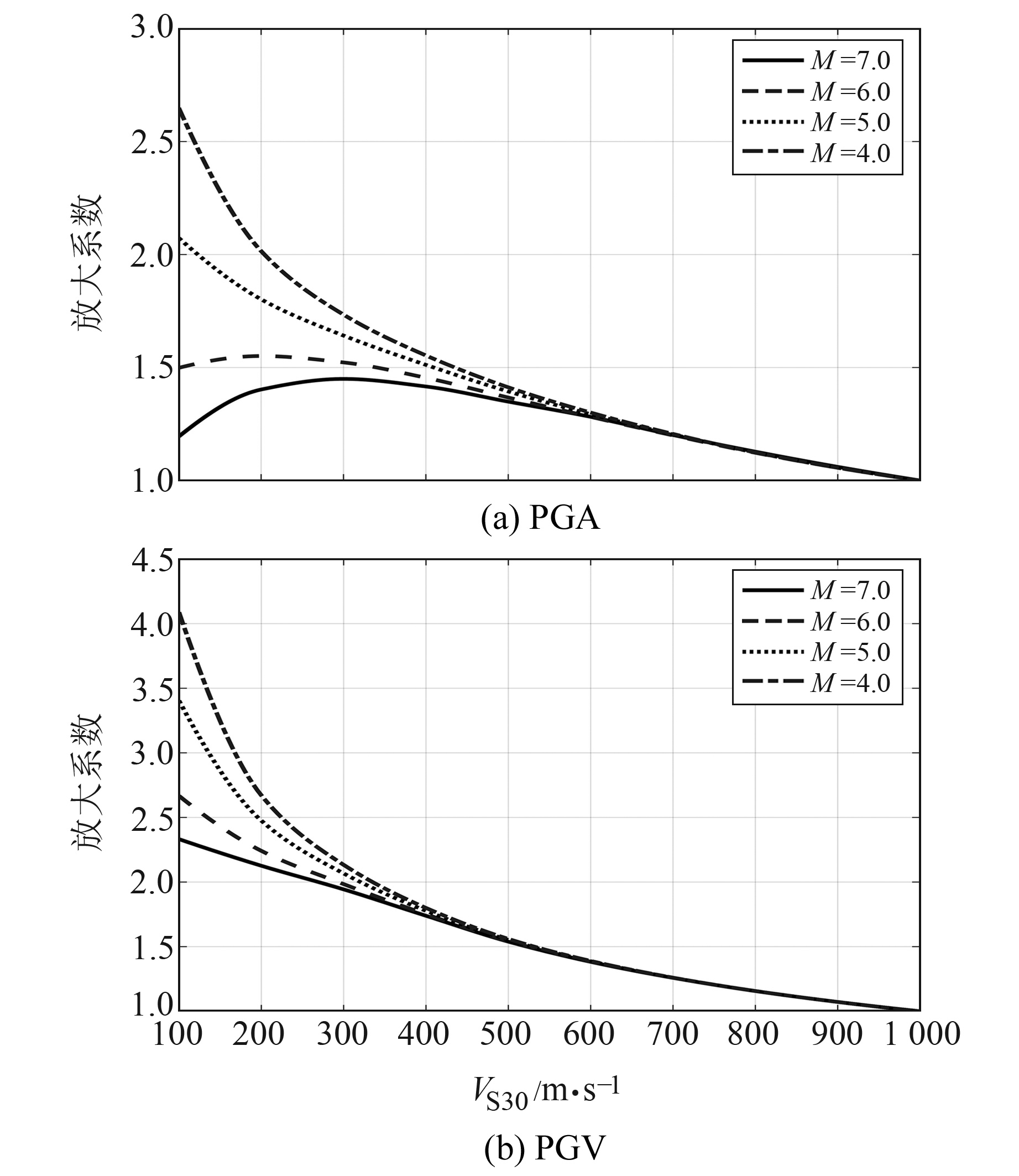
|
图 7 R=25 km时竖向地震动场地放大效应 Fig. 7 Site amplification effect of vertical ground motion at R=25 km |
图 7中的4条曲线分别为M=4.0、5.0、6.0和7.0时近场断层距R=25 km场址处竖向PGA和PGV的场地放大系数。由图 7(a)可以发现,在300 m/s<VS30<1 000 m/s范围内,随着VS30的减小,4个震级条件下PGA的放大系数均呈现出不断增大的趋势,说明竖向地震动PGA呈现出场地放大效应;而在100 m/s≤VS30≤300 m/s范围内,M=4及M=5时仍然维持了之前的放大系数,仍呈现出放大系数随剪切波速减小而增大的特征;但M=6及M=7时出现了放大系数随剪切波速减小而降低的特征。上述特点说明,随着震级的增大(地震动的增大),大震条件下的软土场地开始呈现出减震效应。
由图 7(b)可见,400 m/s<VS30<1 000 m/s范围内,震级M的变化对不同剪切波速条件下PGV的场地放大系数影响不大;而在100 m/s≤VS30≤300 m/s范围内,即软土场地条件下,随着震级M的减小,其场地放大效应愈发显著。随着剪切波速的降低,前者放大效应一直增加,而后者由于先放大后滤波的作用,呈现出明显的减震效应。
4 结语本文提出一种基于随机自适应神经模糊推理系统(ANFIS)的竖向地震动参数预测模型,可为地震危险性判定、地震灾害评价和工程结构抗震建设等提供快速有效的地震动参数估计。ANFIS竖向地震动参数预测模型获得的地震动衰减特征具备震级效应、场地放大效应及PGA软土减震效应特征,与其他模型相比具有更好的预测精度。
| [1] |
李宁, 刁泽民, 李忠献. 考虑震源和场地特征的近断层地区竖向地震动合成研究[J]. 工程力学, 2022, 39(6): 181-190 (Li Ning, Diao Zemin, Li Zhongxian. Study on Synthesis Method of Vertical Ground Motions for Near-Fault Regions Considering the Characteristics of Source and Site Condition[J]. Engineering Mechanics, 2022, 39(6): 181-190)
(  0) 0) |
| [2] |
管仲国, 黄勇, 张昊宇, 等. 青海玛多7.4级地震桥梁工程震害特性分析[J]. 世界地震工程, 2021, 37(3): 38-45 (Guan Zhongguo, Huang Yong, Zhang Haoyu, et al. Damage Characteristics and Analysis of Bridge Engineering in M7.4 Qinghai Maduo Earthquake[J]. World Earthquake Engineering, 2021, 37(3): 38-45)
(  0) 0) |
| [3] |
Abrahamson N, Silva W. Summary of the Abrahamson and Silva NGA Ground-Motion Relations[J]. Earthquake Spectra, 2008, 24(1): 67-97 DOI:10.1193/1.2924360
(  0) 0) |
| [4] |
卢滔, 薄景山, 李巨文, 等. 汶川大地震汉源县城建筑物震害调查[J]. 地震工程与工程振动, 2009, 29(6): 88-95 (Lu Tao, Bo Jingshan, Li Juwen, et al. Damage to Buildings in Hanyuan County Town during 2008 MS8.0 Wenchuan Earthquake[J]. Journal of Earthquake Engineering and Engineering Vibration, 2009, 29(6): 88-95)
(  0) 0) |
| [5] |
谢俊举, 温增平, 高孟潭, 等. 2008年汶川地震近断层竖向与水平向地震动特征[J]. 地球物理学报, 2010, 53(8): 1796-1805 (Xie Junju, Wen Zengping, Gao Mengtan, et al. Characteristics of Near-Fault Vertical and Horizontal Ground Motion from the 2008 Wenchuan Earthquake[J]. Chinese Journal of Geophysics, 2010, 53(8): 1796-1805)
(  0) 0) |
| [6] |
Segou M, Voulgaris N. Proschema: A MATLAB Application for Processing Strong Motion Records and Estimating Earthquake Engineering Parameters[J]. Computer Science, 2010, 36(7): 977-986
(  0) 0) |
| [7] |
赵德宏, 张帅. 基于ANFIS算法的天然石材铣削加工条件下的切削载荷预测方法[J]. 沈阳建筑大学学报: 自然科学版, 2022, 38(3): 535-542 (Zhao Dehong, Zhang Shuai. Research on Cutting Force Prediction under the Milling Condition of Natural Stone Based on ANFIS Algorithm[J]. Journal of Shenyang Jianzhu University: Natural Science, 2022, 38(3): 535-542)
(  0) 0) |
| [8] |
邓伟伟, 段朝阳, 闫亮. 基于自适应神经模糊推理系统的导弹直/气复合控制系统设计[J]. 导航定位与授时, 2021, 8(5): 54-60 (Deng Weiwei, Duan Chaoyang, Yan Liang. Design of Missile Direct/Air Compound Control System Based on Adaptive Neuro-Fuzzy Inference System[J]. Navigation Positioning and Timing, 2021, 8(5): 54-60)
(  0) 0) |
2. School of Civil Engineering, Architecture and the Environment, Hube University of Technology, 28 Nanli Road, Wuhan 430068, China
 2023, Vol. 43
2023, Vol. 43


