2. 江西省自然资源测绘与监测院,南昌市站前西路159号,330009
对流层延迟是影响GNSS定位精度的主要误差源之一。作为较为常用的2种经验对流层延迟模型,Saastamoinen模型[1]和Hopfield模型[2]需要输入站点实测气象参数,但许多GNSS测站并未配备气象传感器,因此使用时受到限制。GPT系列模型[3-6]可弥补这一缺点,该模型可提供任意位置的气压、温度等气象参数,配合经验对流层模型使用时能取得较好的改正效果。许多学者验证了GPT系列模型在不同地区的精度,并得到了较好的效果[7-9]。
安徽省地处长江三角洲地区,地形地貌特点差异显著,以长江、淮河为界,自南向北被分为皖南、皖中和皖北3个区域,分别以山地、丘陵及平原为主要地貌特征。在气候上,安徽属暖温带与亚热带的过渡区域,淮河以北属暖温带半湿润季风气候,淮河以南属亚热湿润季风气候,独特的气候特征造就了省内差异化的天气变化特点。同时,目前尚无关于GPT3模型在安徽地区的性能分析研究。因此,本文利用安徽省CORS站数据评估GPT3模型在安徽地区的精度,为安徽地区建立高精度的对流层延迟模型提供参考。
1 GPT3模型GPT3模型可以提供1°×1°与5°×5°两种格网分辨率的气压、温度、加权平均温度、水汽递减因子等气象参数。顾及各气象参数的周年、半周年变化项,可表示为[6]:
| $\begin{gathered}y(t)=A_0+A_1 \cos \left(2 \pi \frac{\text { doy }}{365.25}\right)+ \\ A_2 \sin \left(2 \pi \frac{\text { doy }}{365.25}\right)+ \\ A_3 \cos \left(4 \pi \frac{\text { doy }}{365.25}\right)+A_4 \sin \left(4 \pi \frac{\text { doy }}{365.25}\right)\end{gathered}$ | (1) |
式中,y(t)为格网点处的气象参数值,doy为年积日,A0为年平均振幅,A1、A2为年周期振幅,A3、A4为半年周期振幅。式(1)得到的气象参数为格网点处的值,还需利用式(2)改正到测站高度处:
| $\left\{\begin{aligned} T & =T_0+\mathrm{d} T \mathrm{~d} h \\ P & =P_0 \exp \\ & \left\{-g_m \frac{\mathrm{d} M_{\mathrm{tr}}}{R_g T_0(1+0.6077 Q)} \mathrm{d} h\right\} \\ e_0 & =Q \frac{P}{0.622+0.378 Q} \\ e & =e_0\left(100 \frac{P}{P_0}\right)^{\lambda+1}\end{aligned}\right.$ | (2) |
式中,T0、P0、e0为格网点的气压(单位hPa)、温度(单位℃)与水汽压(单位hPa),T、P、e为归一化到测站高度的气压、温度与水汽压,dT为温度递减率(单位K/km),Q为比湿(单位g/kg),gm为重力加速度,取9.806 65 m/s2,dMtr为干空气摩尔质量,取28.965×10-3 kg/mol,Rg为气体常数,取8.314 3 J/(K ·mol),λ为水汽递减因子。最后采用空间双线性内插计算得到测站处的气象参数,再结合Saastamoinen模型及Hopfield模型计算出测站ZTD值。
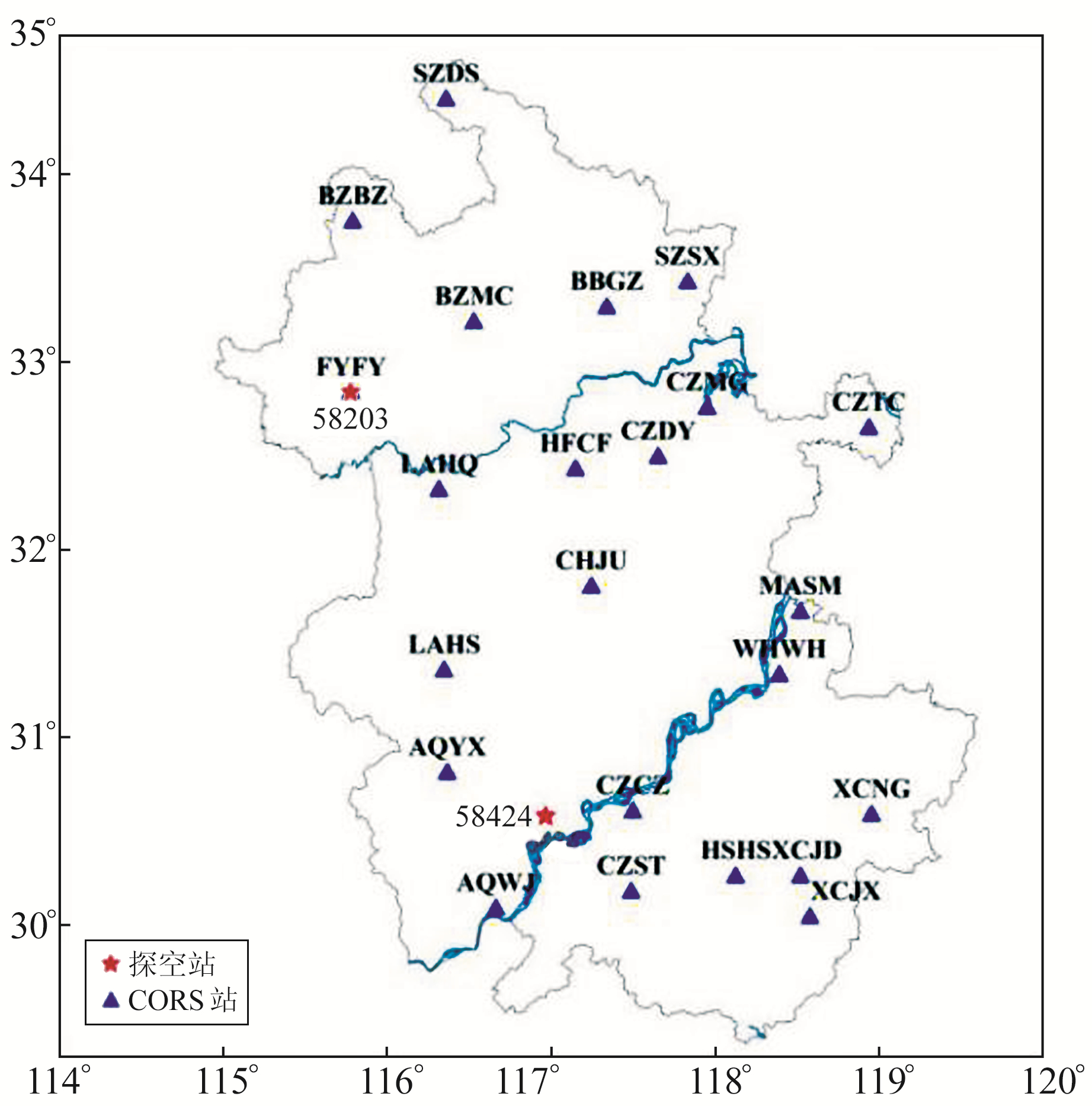
2 数据及方法 2.1 数据来源选取2017年安徽地区23个CORS站的GNSS观测数据及2个探空站的气象数据,同时利用武汉大学PPP-AR软件[10-11]计算出站点ZTD值,解算策略见表 1。图 1为安徽区域CORS站和探空站分布,其中CORS站FYFY与探空站58203共址,探空站58424无共址站,但与AQWJ站相距仅40 km,因此2个探空站可作为验证PWV及Tm的参考。
|
|
表 1 数据处理策略 Tab. 1 Data processing strategy |
|
图 1 CORS站与探空站分布 Fig. 1 Distribution of CORS stations and radiosonde stations |
本文对比分析中涉及几种PWV计算方式,在此作简单介绍。
2.2.1 Tm计算Tm是反演PWV必不可少的关键参数之一,可由数值积分法计算得到:
| $T_m=\frac{\int \frac{e}{T} \mathrm{~d} h}{\int \frac{e}{T^2} \mathrm{~d} h}=\frac{\sum\limits_{i=1}^n\left(\frac{e_i}{T_i}\right) \Delta h_i}{\sum\limits_{i=1}^n\left(\frac{e_i}{T_i^2}\right) \Delta h_i}$ | (3) |
式中,ei为第i层的平均水汽压,Ti为第i层的平均温度,Δhi为第i层大气的厚度。其中,水汽压e需要通过经验公式进行计算:
| $e=6.112 \times \exp (17.62 t /(243.12+t))$ | (4) |
式中,t为露点温度。本文以2个探空站数值积分得到的Tm作为参考值,评估分析GPT3模型的Tm精度。
2.2.2 GNSS-PWV计算利用PPP解算软件解算CORS站数据获取ZTD值,扣除由Saastamoinen模型计算得到的天顶对流层干延迟(ZHD),最终得到天顶对流层湿延迟(ZWD),进而通过转换系数计算得到PWV(GNSS-PWV):
| $\left\{\begin{array}{l}\mathrm{PWV}=\varPi \times \mathrm{ZWD} \\ \varPi=\frac{10^6}{\rho_w R_v\left(k_3 / T_m+k_2^{\prime}\right)}\end{array}\right.$ | (5) |
式中,Π为无量纲比例因子,ρw为液态水密度,Rv=461.495 J/(kg ·K)为水汽的气体常数,k3=3.776×105 K2/hPa、k2′=22.13 K /hPa均为大气折射常数。
2.2.3 探空站PWV计算探空站PWV(RS-PWV)利用比湿数据积分公式计算得到:
| $\left\{\begin{array}{l}\mathrm{PWV}=\frac{1}{g_m} \int_{P_z}^{P_0} q \mathrm{~d} p \\ q=\frac{622 e}{p-0.378 e}\end{array}\right.$ | (6) |
式中,P0为测站地面气压,Pz为z高度上的气压,q为各气压层比湿。
3 结果与分析 3.1 GPT3模型的ZTD精度评估图 2为利用GPT3模型结合Saastamoinen模型和Hopfield模型计算的2017年安徽省4个CORS站的ZTD值及PPP-AR解算的ZTD值时序分布。总体而言,GPT3+Sasstamoinen和GPT3+Hopfield组合模型都能较好地反映出ZTD的变化趋势,但由于GPT3提供的气象参数仅顾及了周年和半周年变化项,ZTD分布较为平滑。与PPP-ZTD相比,GPT3-ZTD的误差具有明显的时空变化特征。在doy150~270时段GPT3-ZTD与PPP-ZTD差异较大,其余时段吻合较好。4个测站中,南部XCJD站的精度最差,GPT3+Sasstamoinen组合模型的平均偏差和RMS分别为-3.45 cm和7.24 cm,明显大于中部及北部测站,北部BZMC站GPT3+Sasstamoinen组合模型的精度分别为-1.66 cm和6.04 cm。进一步对比发现,4个测站中Saastamoinen模型和Hopfield模型在不同时段性能也有明显差异。其中,AQWJ站和CHJU站2种模型在doy150~270时段差异较大,其他时段差异较小;XCJD站几乎全年都存在差异,而BZMC站具有差异的时段相对较少。

|
图 2 PPP-ZTD和GPT3-ZTD时间序列 Fig. 2 PPP-ZTD and GPT3-ZTD time series |
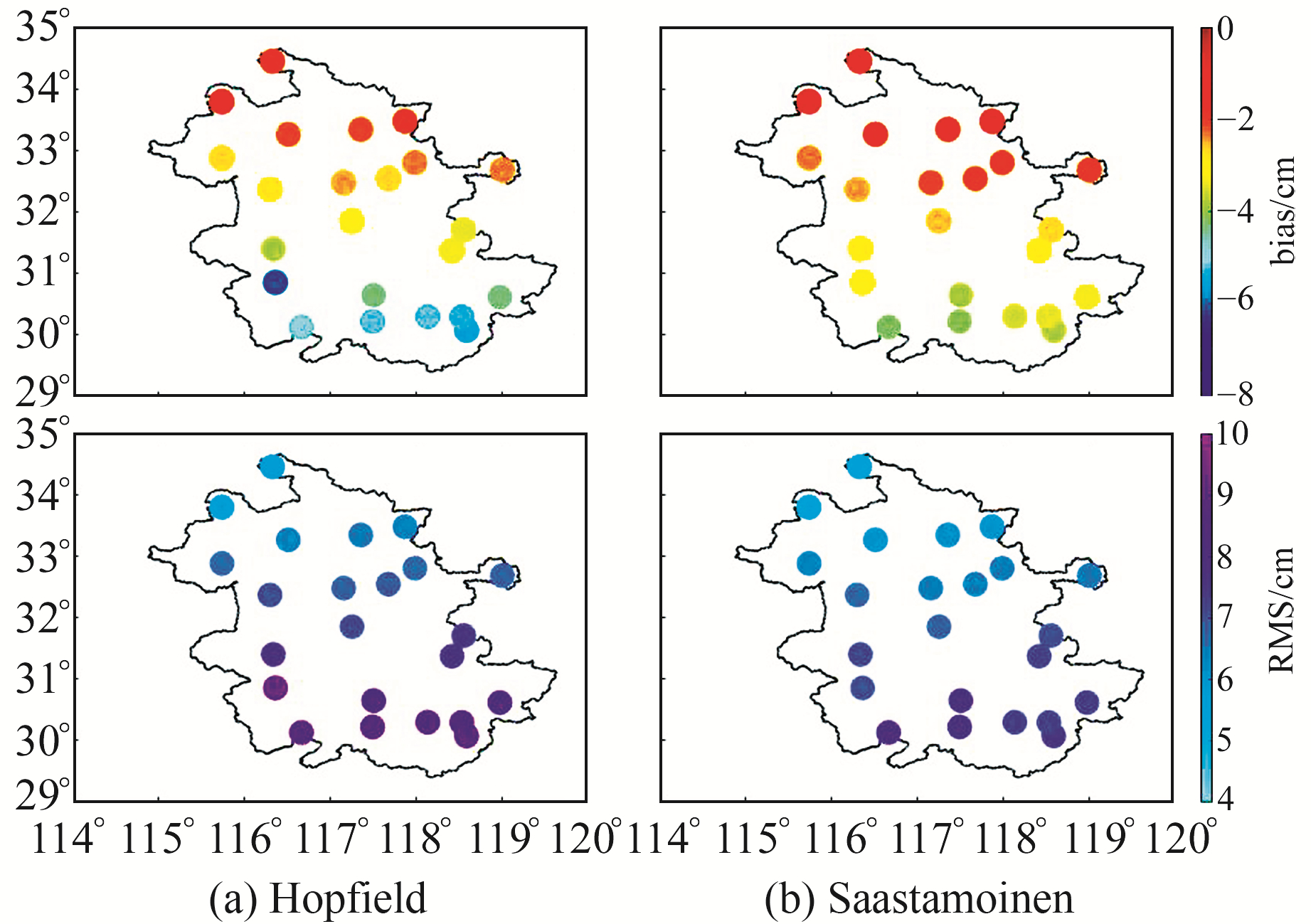
通过上述分析可知,GPT3模型在安徽地区具有明显的空间差异性。为进一步分析这种差异性,计算其余测站的bias和RMS,结果如图 3和表 2(单位cm)所示,在安徽区域GPT3+Sasstamoinen组合模型和GPT3+Hopfield组合模型的ZTD精度自北向南逐渐降低;在皖北区域2种模型的平均bais分别为-1.65 cm和-2.01 cm,而在皖南区域精度分别降至-3.45 cm和-4.58 cm。这是因为安徽省内各区域降水差异较大, 呈南多北少、山区多平原少的特点[12],而皖南地区多为山区,皖北地区多为平原。结合图 2可知,GPT3模型在doy150~270误差较大,相比于皖北区域,皖南地区在该时段降雨尤其充沛,且雨期较长,从而导致GPT3模型在皖南地区精度较差。相比于GPT3+Hopfield组合模型来说,GPT3+Sasstamoinen组合模型在安徽区域的精度稍高,其bias和RMS分别为-2.56 cm和6.7 cm。此外,与PPP-ZTD相比,GPT3-ZTD整体呈负向偏差,表明GPT3模型低估了安徽区域的ZTD。
|
图 3 安徽省23个CORS站的GPT3模型精度 Fig. 3 Accuracy of GPT3 model at 23 CORS stations in Anhui province |
|
|
表 2 不同对流层模型的bias和RMS Tab. 2 bias and RMS of different tropospheric models |
由图 2可知,GPT3模型除了在空间上具有差异性外,在不同时段也具有明显的差异。为进一步分析GPT3模型的季节性变化特征,统计春季(3~5月)、夏季(6~8月)、秋季(9~11月)、冬季(12~2月)4个季节的精度信息,如表 3(单位cm)所示。可以看出,GPT3模型在春、冬季的精度明显优于夏、秋季,春季和冬季的bias不超过-1.0 cm,而夏季精度低于-5.0 cm。对于皖南一些站点来说,如XCJX站GPT3+Sasstamoinen组合模型夏季bias和RMS达到-7.0 cm和8.7 cm,而GPT3+Hopfield组合模型的误差甚至超过-9.5 cm和10.8 cm。因此,为了能够利用GPT3模型获得较好的对流层延迟改正效果,尤其是在皖南区域夏、秋季节,需结合当地的气象数据对GPT3模型作精化处理。
|
|
表 3 组合模型在不同季节的精度信息 Tab. 3 Precision of combination models in different seasons |
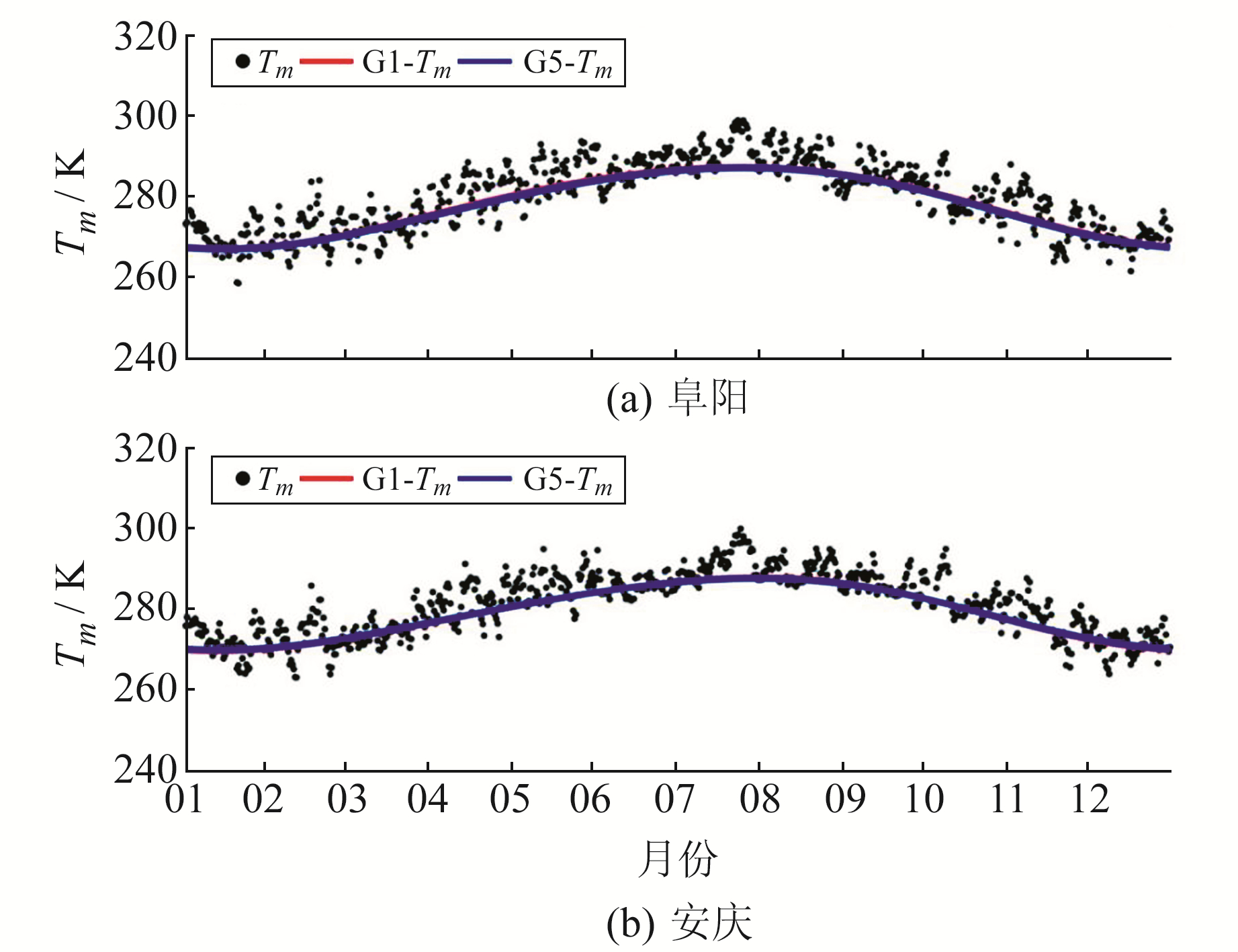
由式(3)可知,Tm是实现ZWD和PWV转换的关键参数。因此,为评估PWV的精度,首先需评估GPT3模型提供的Tm精度。以安徽北部和南部2个国家级探空站(阜阳58203和安庆58424)数值积分得到的Tm作为参考值,统计GPT3两种分辨率(1°×1°和5°×5°)的Tm精度信息。从图 4可以看出,GPT3模型的Tm变化趋势与2个探空站计算的Tm基本一致,Tm值从1月开始逐渐增大至8月,随后逐渐减小。表 4(单位K)给出了Tm的bias和RMS,可以看出,在2个探空站GPT3模型2种分辨率的Tm精度基本相当,bias在-2.0 K左右,RMS在4.5 K左右,与蔡猛等[8]的研究结果较为接近,表明GPT3模型2种分辨率格网提供的Tm精度较高,能够满足安徽省无实测气象参数时GNSS气象学研究的需求。
|
图 4 2种格网分辨率的GPT3模型Tm时序分布 Fig. 4 Tm time series of GPT3 model with two grid resolutions |
|
|
表 4 2种分辨率Tm的精度统计 Tab. 4 Accuracy statistics of two resolutions of Tm |
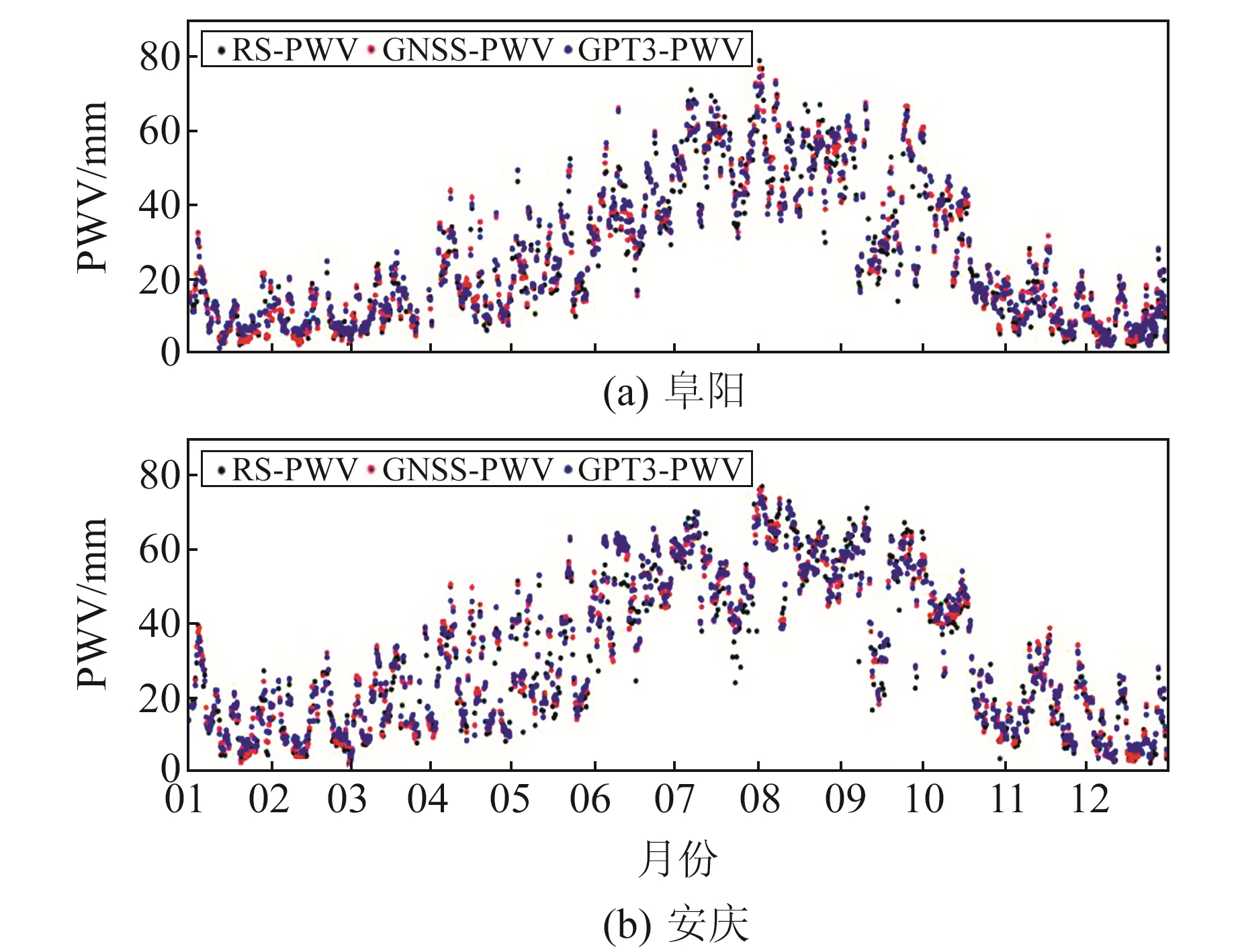
为分析GPT3模型反演PWV的精度,选取1°×1°格网GPT3模型反演的PWV(GPT3-PWV)与基于实测气象参数反演的PWV(GNSS-PWV)及RS-PWV进行对比分析,其中GPT3-PWV与GNSS-PWV均采用式(5)进行计算。由图 5可知,3种方法计算的PWV整体变化趋势相似,具有较高的一致性。
|
图 5 安庆站和阜阳站的PWV Fig. 5 PWV at FYFY and AQWJ |
为研究GPT3模型反演PWV的时空特征,给出安徽区域GPT3-PWV的时空分布。由图 6可知,GPT3-PWV表现出显著的季节性特征,PWV值在冬季最小、夏季最大,且PWV值在空间上呈现出由皖南向皖北逐渐减小的特征。这是因为冬季比较干燥,夏季降雨多、水汽活动剧烈,且与安徽省降水呈由南向北递减、山区多平原少的空间分布规律有关[12]。表 5(单位mm)以RS-PWV为参考值统计了GPT3-PWV和GNSS-PWV在4个季节及全年的精度,可以看出,反演的PWV在春、冬季的精度要优于夏、秋季。对于冬季而言,RMS均不超过3 mm,而在夏季甚至高达5.7 mm。同时,GPT3-PWV精度较高,仅比GNSS-PWV略低0.3~0.5 mm。因此,在缺少实测气象数据时,可采用GPT3模型气象参数反演的PWV作为替代。

|
图 6 GPT3-PWV的时空分布 Fig. 6 Spatio-temporal distribution of GPT3-PWV |
|
|
表 5 PWV精度统计 Tab. 5 PWV accuracy statistics |
本文利用2017年安徽省CORS站的观测数据及探空站数据,评估GPT3模型反演的ZTD、Tm及PWV的精度信息。结果表明:
1) GPT3模型的反演精度在安徽区域具有明显的时空分布特征,ZTD精度自北向南逐渐降低,且春、冬季精度优于夏、秋季。同时,GPT3模型普遍低估了安徽地区的ZTD。
2) 在相同气象参数条件下,GPT3+Sasstamoinen组合模型的ZTD精度要优于GPT3+Hopfield,二者的差异在皖北较小,但自北向南逐渐变大,进一步反映Saastamoinen模型比Hopfield模型更适用于安徽地区。
3) 在安徽地区,GPT3模型2种格网分辨率的Tm精度基本相当,平均偏差在-2.0 K左右,RMS在4.5 K左右。
4) 基于GPT3模型气象参数反演的PWV与探空站的PWV具有较高的一致性,GPT3-PWV在空间上由皖南向皖北逐渐减小,且夏季最大、冬季最小。PWV精度表现出明显的季节性特征,春、冬季的精度优于夏、秋季。GPT3-PWV的精度较高,仅比GNSS-PWV略低0.3~0.5 mm。
| [1] |
Saastamoinen J. Introduction to Practical Computation of Astronomical Refraction[J]. Bulletin Géodésique, 1972, 106(1): 383-397 DOI:10.1007/BF02522047
(  0) 0) |
| [2] |
Hopfield H S. Tropospheric Effect on Electromagnetically Measured Range: Prediction from Surface Weather Data[J]. Radio Science, 1971, 6(3): 357-367 DOI:10.1029/RS006i003p00357
(  0) 0) |
| [3] |
Böhm J, Heinkelmann R, Schuh H. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications[J]. Journal of Geodesy, 2007, 81(10): 679-683 DOI:10.1007/s00190-007-0135-3
(  0) 0) |
| [4] |
Lagler K, Schindelegger M, Böhm J, et al. GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters, 2013, 40(6): 1 069-1 073 DOI:10.1002/grl.50288
(  0) 0) |
| [5] |
Böhm J, Möller G, Schindelegger M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere(GPT2w)[J]. GPS Solutions, 2015, 19: 433-441 DOI:10.1007/s10291-014-0403-7
(  0) 0) |
| [6] |
Landskron D, Böhm J. VMF3/GPT3: Refined Discrete and Empirical Troposphere Mapping Functions[J]. Journal of Geodesy, 2018, 92(4): 349-360 DOI:10.1007/s00190-017-1066-2
(  0) 0) |
| [7] |
黄良珂, 李琛, 黄军胜, 等. 广西地区GPT2w对流层延迟模型适用性分析[J]. 桂林理工大学学报, 2018, 38(2): 289-294 (Huang Liangke, Li Chen, Huang Junsheng, et al. Assessment of GPT2w Tropospheric Delay Model over Guangxi[J]. Journal of Guilin University of Technology, 2018, 38(2): 289-294)
(  0) 0) |
| [8] |
蔡猛, 刘立龙, 黄良珂, 等. GPT3模型反演GNSS大气可降水量精度评定[J]. 大地测量与地球动力学, 2022, 42(5): 483-488 (Cai Meng, Liu Lilong, Huang Liangke, et al. Evaluation of GNSS Precipitable Water Vapor Derived from GPT3 Model[J]. Journal of Geodesy and Geodynamics, 2022, 42(5): 483-488)
(  0) 0) |
| [9] |
黄聪, 郭杭. 基于GPT3模型的ZTD及PWV反演精度分析[J]. 大地测量与地球动力学, 2022, 42(5): 489-493 (Huang Cong, Guo Hang. Accuracy Analysis of ZTD and Precipitable Water Vapor Inversion Based on GPT3 Model[J]. Journal of Geodesy and Geodynamics, 2022, 42(5): 489-493)
(  0) 0) |
| [10] |
Geng J H, Yang S F, Guo J. Assessing IGS GPS/Galileo/BDS-2/BDS-3 Phase Bias Products with PRIDE PPP-AR[J]. Satellite Navigation, 2021, 2(1): 238-252
(  0) 0) |
| [11] |
Geng J H, Wen Q, Zhang Q Y, et al. GNSS Observable-Specific Phase Biases for All-Frequency PPP Ambiguity Resolution[J]. Journal of Geodesy, 2022, 96(2)
(  0) 0) |
| [12] |
王秋龙. 安徽省近50余年降水量时空变化特征分析[J]. 测绘工程, 2014, 23(11): 19-24 (Wang Qiulong. Temporal and Spatial Distribution of Precipitation over Anhui Province in Recent 50 Years[J]. Engineering of Surveying and Mapping, 2014, 23(11): 19-24)
(  0) 0) |
2. Jiangxi Provincial Institute of Natural Resource Surveying and Monitoring, 159 West-Zhanqian Road, Nanchang 330009, China
 2023, Vol. 43
2023, Vol. 43


