2. 布里斯托大学社会科学与法律学院,12 Priory Road, Bristol BS8 1TX, 英国
总电子含量TEC是用来描述电离层形态和结构的重要物理参数,其数值大小能够间接反映电离层的活跃程度及对无线电信号传播的影响[1-2]。全球导航卫星系统GNSS播发的导航测距信号在穿过电离层时会产生较为严重的定位误差[3],因此TEC的快速估计与短期预报对提高导航定位的精度和研究太阳活动的变化规律具有重要意义[4-5]。
目前,TEC的估计方法主要基于GNSS观测数据,利用GNSS技术提取TEC是建立高精度电离层模型的重要前提[6-7]。以国际GNSS服务组织(IGS)为代表的全球电离层产品GIM为格网形式,这些产品适用于全球大范围的电离层延迟改正,但对于小范围或单站用户而言,大范围或格网点的信息显得多余且精度得不到保证。
随着计算机技术的发展,人工神经网络模型在电离层TEC的预报中得到广泛应用。鲁铁定等[8]建立了经验小波变化和Elman(EWT-Elman)神经网络短期电离层预报模型;Mallika等[9]提出了一种基于主成分分析法和人工神经网络PCA-NN的方法,并对日本上方的格网点进行了预测,准确率达95%;汤俊等[10]建立了基于麻雀搜索算法的改进Elman神经网络,比BP模型和Elman模型效果更优。然而,目前对TEC的预报研究大多基于格网形式,很少对单站TEC进行预报,且仅对格网TEC进行预报难以获取测站上方电离层的变化情况,无法为单基站系统和定位用户提供先验准确的电离层信息。因此,本文采用加权函数的方法计算单站TEC,构建一种神经网络和滑动窗口相结合的TEC短期预报模型,并利用太阳活动低年和太阳活动高年数据对模型进行分析验证。
1 原理与方法 1.1 单站TEC估计伪距和载波相位的观测方程如下:
| $\begin{aligned} & P_{k, \mathrm{j}}^{\mathrm{i}}=\rho_{0, \mathrm{j}}^{\mathrm{i}}+d_{\text {ion }, k, \mathrm{j}}^{\mathrm{i}}+d_{\text {trop }, \mathrm{j}}^{\mathrm{i}}+ \\ & c\left(\tau^{\mathrm{i}}-\tau_{\mathrm{j}}\right)+d_k^{\mathrm{i}}+d_{k, \mathrm{j}}+\varepsilon_{P, k, \mathrm{j}}^{\mathrm{i}}\end{aligned}$ | (1) |
| $\begin{gathered}L_{k, \mathrm{j}}^{\mathrm{i}}=\rho_{0, \mathrm{j}}^{\mathrm{i}}-d_{\mathrm{ion}, k, \mathrm{j}}^{\mathrm{i}}+d_{\text {trop }, \mathrm{j}}^{\mathrm{i}}+ \\ c\left(\tau^{\mathrm{i}}-\tau_{\mathrm{j}}\right)-\lambda b_{k, \mathrm{j}}^{\mathrm{i}}-\lambda N_{k, \mathrm{j}}^{\mathrm{i}}+\varepsilon_{L, k, \mathrm{j}}^{\mathrm{i}}\end{gathered}$ | (2) |
式中,P和L分别为伪距和载波相位的观测值,ρ为卫星和接收机的实际距离,dion和dtrop分别为电离层延迟和对流层延迟,τi和τj分别为卫星和接收机的钟误差,d为卫星和接收机的差分码偏差,b为卫星和接收机的相位超前,N为载波相位模糊度,ε为测量误差。
分别对式(1)和式(2)作差,消除频率无关项。考虑到伪距观测值噪声较大,采用载波相位平滑伪距方法提高TEC估计精度,通过投影函数将STEC转化为垂直方向上的VTEC。球谐函数模型表达式为:
| $\begin{aligned} & E(\beta, s)=\sum\limits_{n=0}^{n_{\max }} \sum\limits_{m=0}^n \widetilde{P}_{m m} \sin \beta \times \\ & \left(a_{n m} \cos (m s)+b_{n m} \sin (m s)\right)\end{aligned}$ | (3) |
式中,E(β, s)为VTEC;β和s分别为穿刺点处的地磁纬度和日固经度;anm、bnm分别为球谐函数模型系数;nmax为球谐函数展开式的最高阶数,本文取4;
在电离层建模中,大部分电离层产品都基于格网或穿刺点处的TEC,适用于大范围电离层改正;但对于小范围甚至单站用户而言,大范围或格网点的信息会显得多余且精度得不到保证。因此,本文引入一种快速可靠的加权方法来获取测站上方VTEC,为单基站系统和定位用户提供电离层先验信息,使电离层产品快速化,其主要优点包括单站计算量小、加权函数简洁、球谐函数低阶求解系数少等。
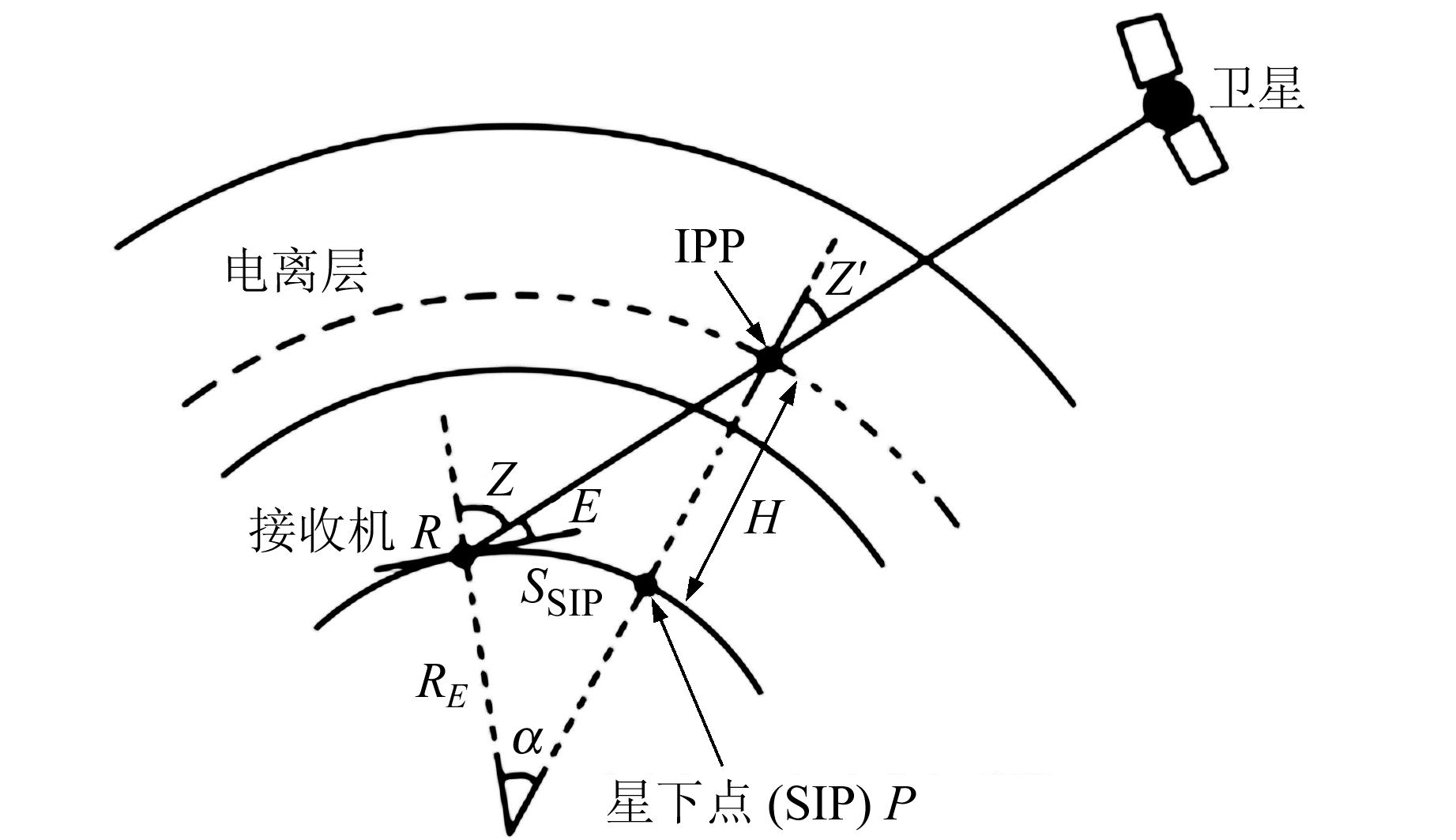
图 1为穿刺点的几何结构,GPS接收机位于R,Z和Z′分别为测站和穿刺点处的天顶角,E为卫星仰角,SSIP为测站R至穿刺点星下点的距离。
|
图 1 穿刺点几何结构 Fig. 1 IPP geometry structure |
由单层假设模型可知,卫星和接收机的连线处都有一个穿刺点,每个穿刺点对应一个VTEC,则某一时刻多个卫星就有多个VTEC值。天顶角Z是测站R到星下点P的距离函数,当SSIP较大、卫星仰角过低时,穿刺点处的VTEC便不能充分代表测站上方的电离层情况。因此,本文将天顶角加权方法引入到每颗卫星中,以此来快速获取测站上方的VTEC[11]。测站上方某一时刻VTEC可表示为:
| $\mathrm{VTEC}=\frac{\sum\limits_{i=1}^n L_i w_i}{\sum\limits_{i=1}^n w_i}$ | (4) |
| $w_i(Z)=\cos ^3 Z$ | (5) |
式中,Li(i=1, 2, …, 32)为同一时刻不同卫星穿刺点处VTEC的估计值。
1.2 TEC短期预报单站TEC可用时间序列表达,神经网络在非线性时间序列的拟合和预测方面效果显著。BP(back propagation)神经网络是目前最成熟、应用最广泛的人工神经网络模型之一,可利用梯度搜索技术使网络的实际输出值和期望输出值误差均方差最小。以TEC为例,训练主要经过2个阶段:首先根据计算出来的TEC进行正向传播输入,然后根据预测结果与真值进行对比,将误差进行反向传播,得到预测结果。
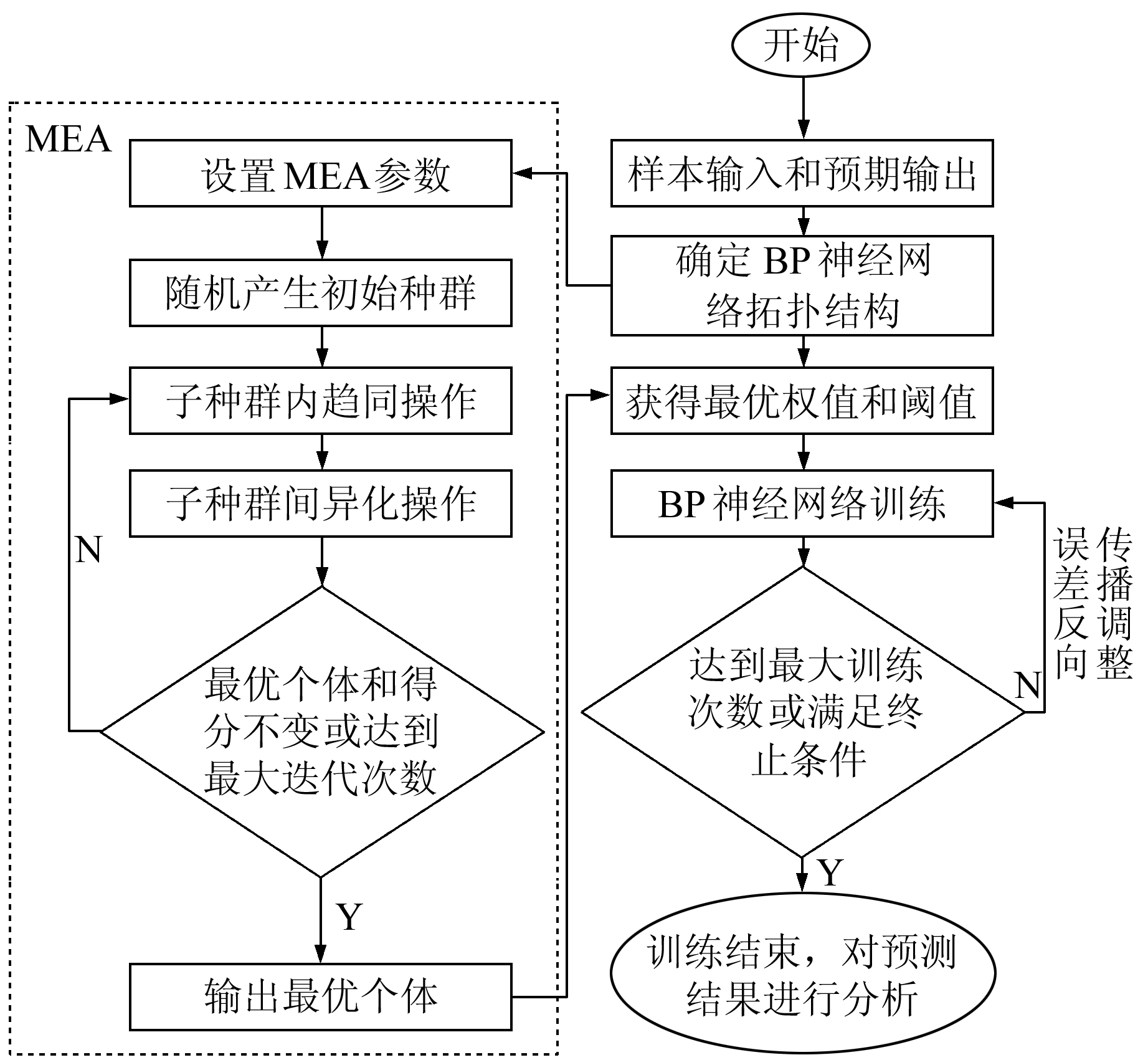
Sun等[12]在1998年针对遗传算法(genetic algorithm, GA)的局限性提出思维进化算法(mind evolutionary algorithm, MEA),该算法保留了GA中“群体”与“进化”的核心内容,同时引进“趋同”和“异化”2种算法。传统的BP神经网络算法容易陷入局部最优且收敛速度慢,MEA能提高收敛速率、缩短网络训练时间,具有较好的预测能力。本文利用MEA来优化BP神经网络的权值和阈值,以期获得更好的预报模型,MEA优化BP神经网络的流程如图 2所示。
|
图 2 MEA优化BP神经网络流程 Fig. 2 BP neural network model optimized by MEA |
通常情况下,基于GNSS-TEC的建模观测数据采样间隔为30 s,1 d内单颗卫星的VTEC至多有2 880个,通过天顶角加权方法可估计出测站连续多日的TEC值。为方便表述,将计算出的多日测站VTEC重新编号为d(d=1, 2, …, N),数据集T可表示为:
| $\boldsymbol{T}=\left[T_1, T_2, \cdots, T_d\right]$ | (6) |
TEC预报模型的精度主要依赖于数学统计模型的准确性。理论上,预报出的结果应与实际值接近,但实际上在太阳活动活跃期和TEC波动剧烈时,预报值与实际值存在较大偏差。由于电离层变化较快且TEC随时间变化明显,基于大窗口或固定窗口的方式并不适用于TEC的短期预报。因此,本文引入滑动窗口与神经网络结合的方法(MW-MEA-BP)对TEC预报值进行质量优化。
本文将滑动窗口宽度设置为1 d,将大小固定的窗口以一定的步长向前滑动,保持样本数目不变,记录每次滑动后TEC的预报值,不断使用新的预测数据取代之前的已知数据,实现连续预报。
1.3 TEC产品生成流程单站TEC估计与预报的具体步骤(图 3)如下:

|
图 3 单站TEC估计与预报基本流程 Fig. 3 Basic process of single-station TEC estimation and forecasting |
1) 基于电离层单层模型,利用GNSS观测数据,采用载波相位平滑伪距,通过投影函数将STEC转化为穿刺点VTEC后与球谐函数模型联立,解出球谐系数,代入式(3)计算穿刺点VTEC,再利用式(4)获取测站上方VTEC;
2) 将计算得到的TEC数据分为训练集、测试集和验证集,通过MEA计算获得最优权值和阈值,代入BP神经网络训练,输出TEC预报模型;
3) 将滑动窗口引入到TEC预报模型中,将大小固定的窗口以一定的步长向前滑动,不断使用新的预测数据来取代之前的已知数据,最终输出TEC预报结果,并与计算所得的TEC进行对比。
2 实验结果与讨论 2.1 单站TEC估计分析本文选取IGS测站观测数据,分别对2014年doy 31~70和2021年doy 157~176、doy 340~359的观测数据进行电离层建模,数据采样间隔为30 s,卫星截止高度角为10°,站点信息如表 1所示。
|
|
表 1 站点信息 Tab. 1 Site information |
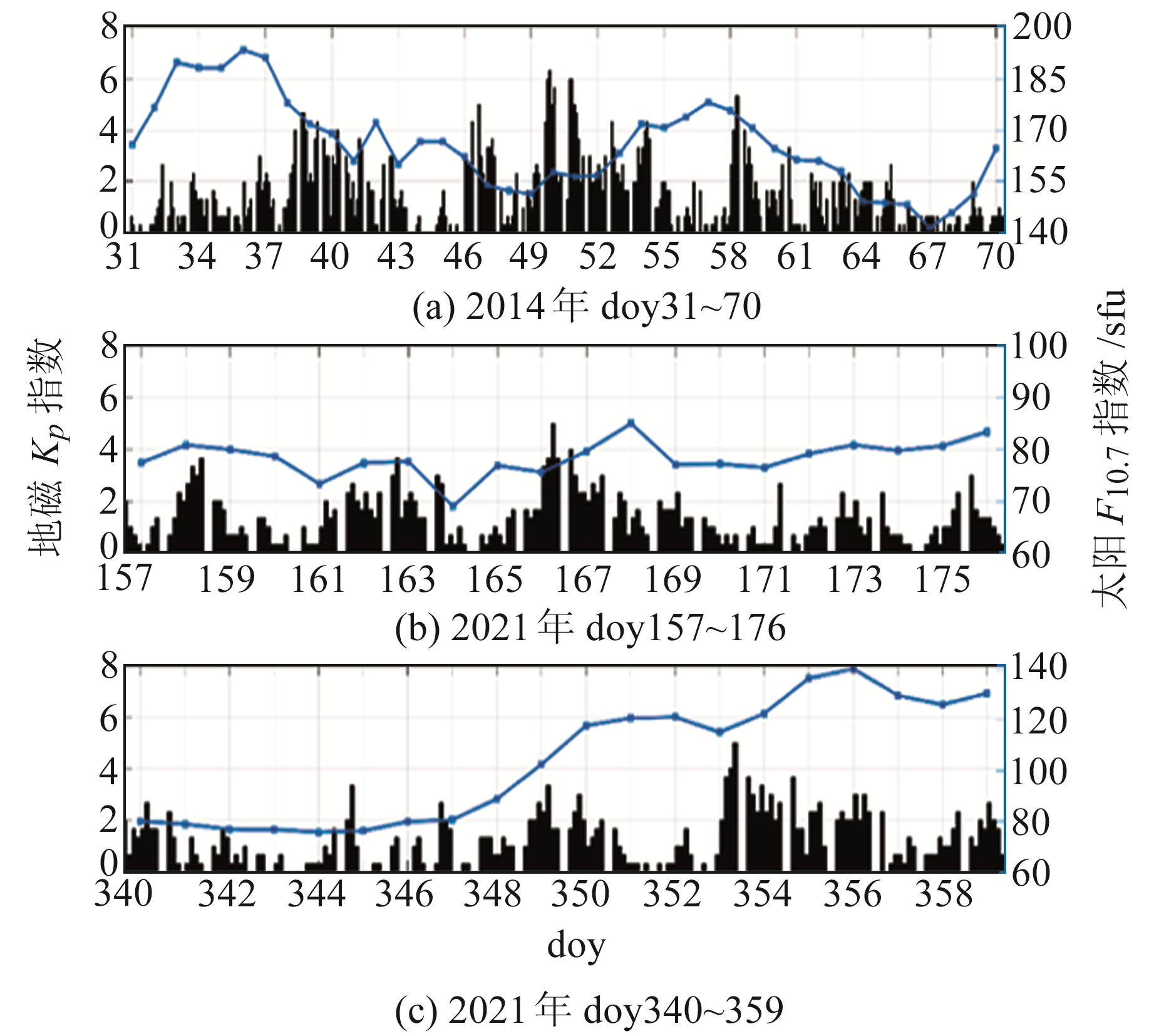
由于受到太阳活动和地磁活动的影响,电离层TEC持续变化,观测时间内的F10.7指数和Kp指数如图 4所示。由图可见,2014年研究时段F10.7指数整体大于140 sfu,太阳活动较为剧烈,属于太阳活动高年;2021-06 F10.7指数小于100 sfu,Kp指数小于5,属于太阳活动低年;2021-12 Kp指数小于5,F10.7指数从doy349开始逐渐增大且大于100 sfu,说明地磁场活动较为平静,但太阳活动开始变活跃。本文分别选取太阳活动高年和太阳活动低年的观测数据进行电离层建模,对比分析使用加权函数预报方法的可行性。
|
图 4 太阳F10.7指数和地磁Kp指数 Fig. 4 Solar F10.7 index andgeomagnetic Kp index |
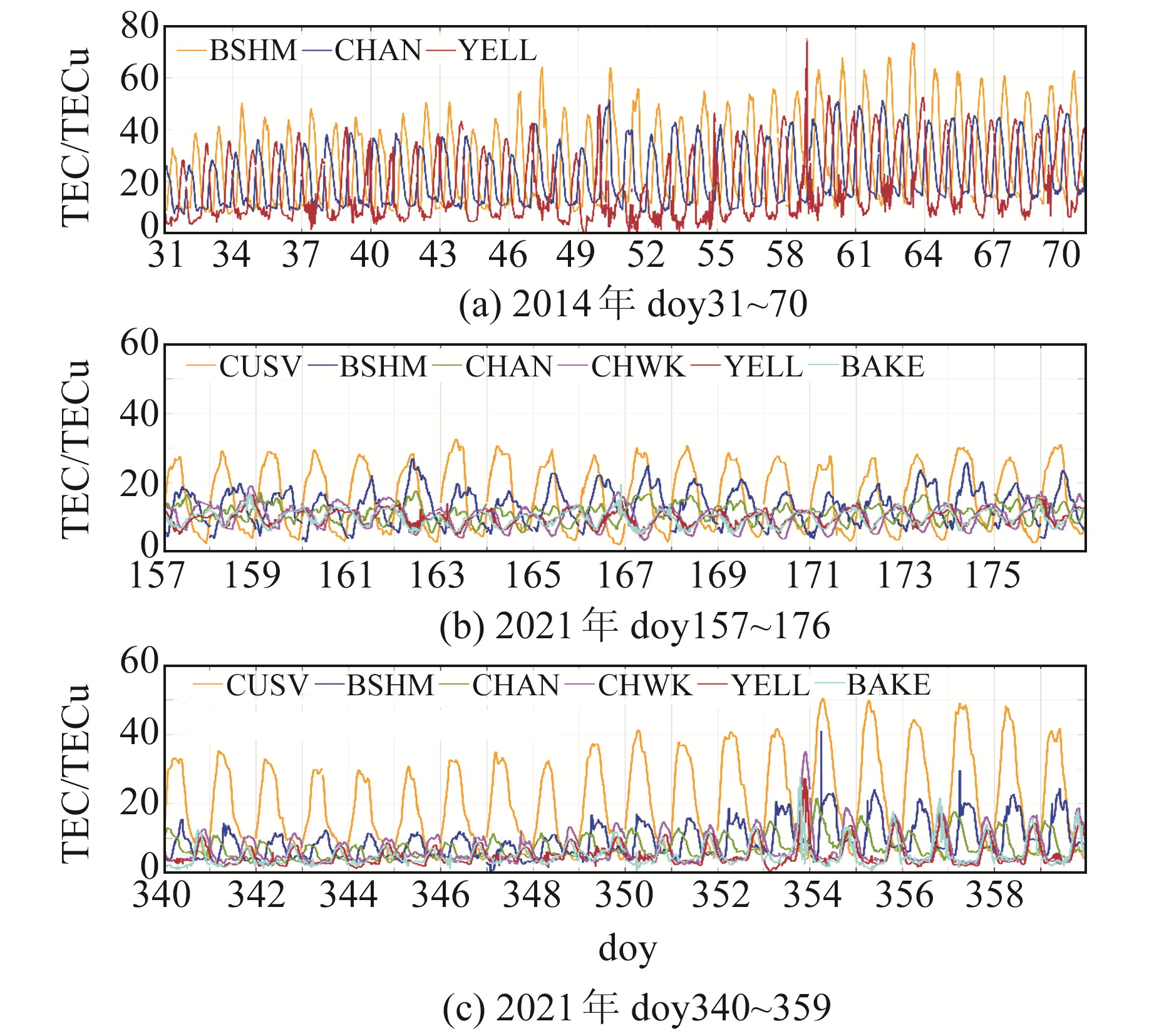
根据上述方法计算单站VTEC,结果如图 5所示。由图可见,低纬度测站的TEC数值最大,中纬度次之,高纬度最小,这是由于地球大气在不同地理位置的组成成分、密度及受太阳的辐射不同。此外,太阳活动高年的测站TEC数值明显大于太阳活动低年,不同纬度带的测站TEC变化趋势一致。2021年doy 353~354、doy 356~357期间,中高纬度测站TEC的波动尤为剧烈,且高纬度出现峰值时间比中低纬度要早,由此可知,此次太阳活动对全球TEC产生的影响并不同步。以上几点变化均与电离层的实际情况相符,由此可以证明,采用加权函数估计测站TEC的方法可靠且快速。
|
图 5 TEC计算结果 Fig. 5 TEC calculation results |
为验证本文算法在TEC预报中的有效性,采用BP模型、MEA-BP模型和MW-MEA-BP模型进行对比分析。在使用神经网络进行TEC预报时,选取1个输入层、3个隐含层和1个输出层的3层网络结构,MEA算法参数设定为种群28 800个、优胜子种群和临时子种群5个、迭代400次。实验数据为2021年doy 157~176共20 d的TEC,选取前10 d的TEC作为网络输入层节点个数,后10 d作为网络输出层节点个数进行网络测试和验证,并对TEC进行归一化处理。将数值控制在[-1, 1]范围内,便于网络训练。将预报得到的TEC与实际TEC进行对比,利用均方根误差RMSE、均值Mean和残差Δ对结果精度进行评定,具体计算公式为:
| $\mathrm{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(x_{\text {true }}-x_i\right)^2}$ | (7) |
| $\operatorname{Mean}=\frac{1}{n} \sum\limits_{i=1}^n\left|x_{\mathrm{true}}-x_i\right|$ | (8) |
| $\varDelta=\left|x_{\text {true }}-x_i\right|$ | (9) |
式中,n为预报数据长度,xi为预报数据,xtrue为实际数据。
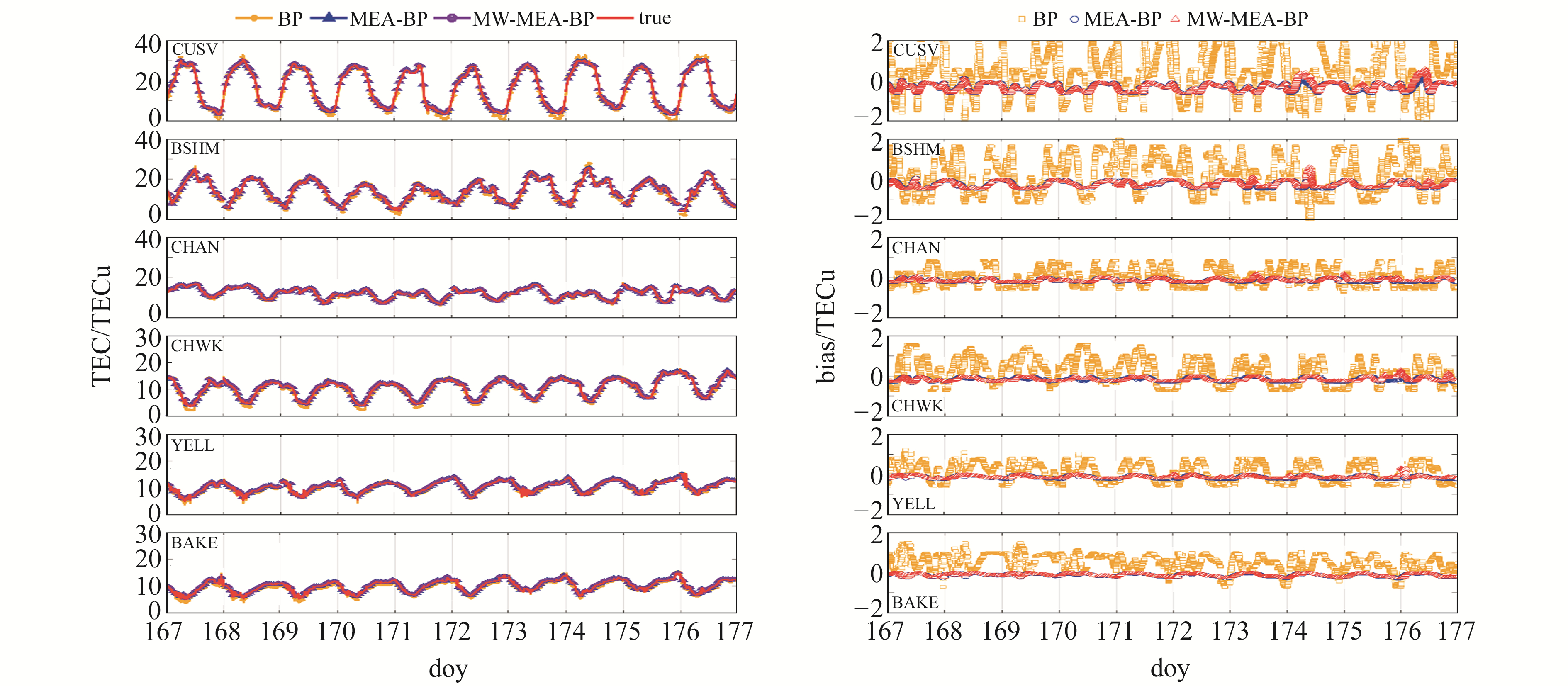
图 6为各测站2021年doy 167~177不同模型预报值与实际值的TEC比较结果,偏差指实际值与预报值之间的差值。结合图 6和表 2(单位TECu)可以看出,相较于BP模型,MEA-BP模型的RMSE和Mean有较为明显的提高。MW-MEA-BP模型较MEA-BP模型的改善效果并不明显,各测站MEA-BP模型的RMSE较BP模型提高68%~80.3%,且测站的RMSE随纬度的增加而减少。这是因为,不同纬度之间TEC的含量和变化特征存在差异,且中高纬度地区测站的TEC日变化幅度较小。
|
图 6 2021年doy 167~177 TEC预报结果与偏差 Fig. 6 TEC forecast results and bias of doy 167-177, 2021 |
|
|
表 2 2021-06各测站10 d预报结果统计 Tab. 2 Statistics of 10 d forecast results of each station in June, 2021 |
为更加直观地描述各模型之间的预报偏差,本文将预报残差进行百分比统计,结果见表 3(单位%)。从结果来看,BP模型的预报值大部分集中在TEC实际值的下方,且拐点处存在较多误差时,TEC日变化幅度较大,RMSE也相应较大,CHAN、YELL、BAKE测站的TEC日变化幅度较小,相对应的RMSE也较小。所有测站MEA-BP模型和MW-MEA-BP模型的残差均小于1 TECu,说明二者具有较好的预报精度。
|
|
表 3 2021年doy167~177预报值残差百分比统计 Tab. 3 Forecast value residual percentage statistics of doy167-177, 2021 |
图 7为各测站2021-12的TEC预报结果与残差分布,结合图 7和表 4(单位TECu)可以看出,在太阳活动较活跃的12月,各测站MEA-BP模型的RMSE较BP模型提高了67.2%~79.4%;MW-MEA-BP模型的RMSE较MEA-BP模型提高了13.9%~54.4%,较BP模型提高了71.%~90.6%。2021年doy 353~354、doy 356~357期间,受F10.7增大的影响,中高纬度地区TEC波动尤为剧烈,部分测站预报残差超过3 TECu。整体来看,MW-MEA-BP模型预报的TEC与真实TEC更为接近,与2021-06太阳活动平静期相比,2021-12TEC日波动范围变大,易产生较大的TEC预报残差。由表 5(单位%)可见,经MW-MEA-BP模型改进后,超过97%的TEC预报值残差在1 TECu之内,但仍有小部分残差超过3 TECu,说明在太阳活动活跃期TEC变化较为剧烈时,本文模型对TEC峰值的预报仍有改进空间。

|
图 7 2021年doy350~359 TEC预报结果与偏差 Fig. 7 TEC forecast results and bias of doy350-359, 2021 |
|
|
表 4 2021-12各测站10 d预报结果统计 Tab. 4 Statistics of 10 d forecast results of each station in December, 2021 |
|
|
表 5 预报值残差百分比统计 Tab. 5 Forecast value residual percentage statistics |
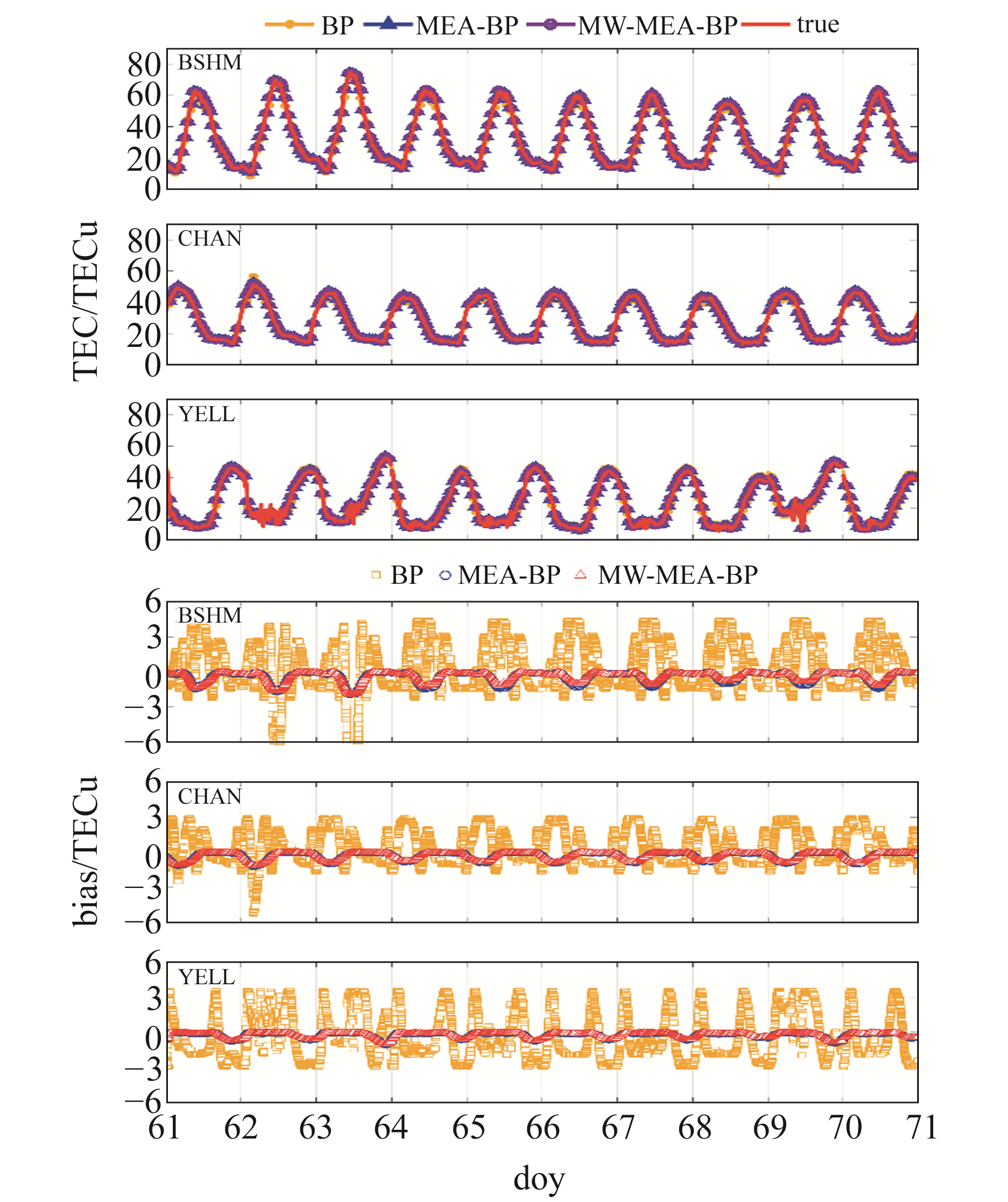
为进一步分析MEA-BP模型和MW-MEA-BP模型预测TEC的可行性,利用2014年doy 31~70的TEC数据进行验证分析,采用前30 d预测后10 d的方法对电离层TEC进行计算。3个测站预测的TEC结果与残差分布如图 8所示。
|
图 8 2014年doy61~70 TEC预报结果与偏差 Fig. 8 TEC forecast results and bias of doy61-70, 2014 |
结合图 8与表 6(单位TECu)、表 7(单位%)可以看出,在太阳活动高年,相较于BP模型,MEA-BP模型的RMSE和Mean有较为明显的提高,MEA-BP模型的RMSE较BP模型分别提高了71.9%、69.8%、84.9%,经MEA-BP模型改进后的残差值均小于2 TECu。由于太阳活动高年各测站TEC日变化幅度大,TEC峰值较为稳定,相较于基于滑动窗口改进的MEA-BP模型,MW-MEA-BP模型的改善效果并不明显。
|
|
表 6 2014年doy61~70 TEC预报结果统计 Tab. 6 Statistics of TEC forecast results of doy61-70, 2014 |
|
|
表 7 2014年doy61~70预报值残差百分比统计 Tab. 7 Forecast value residual percentage statistics of doy61-70, 2014 |
综上可知,MEA-BP模型预报方法较BP模型有明显改进。在太阳活动活跃期TEC变化较为剧烈时,相比于MEA-BP模型,MW-MEA-BP模型能进一步改善TEC拐点处的预报值,具有一定的优越性;在太阳活动平静期,MW-MEA-BP模型和MEA-BP模型精度相当。
3 结语1) 基于加权函数计算得到的测站TEC变化特性与电离层实际情况相符,说明本文方法快速可靠。
2) 基于滑动窗口改进的MEA-BP模型在太阳活动低年和太阳活动高年都有着较好的预报精度,相比于传统BP模型和MW-MEA-BP模型,MEA-BP模型能提高TEC的预报精度。
综上所述,本文结果可为单站电离层TEC模型的建立提供理论依据,对TEC时空变化、电离层TEC预报、电离层异常监测等研究有一定的参考意义。
| [1] |
袁运斌, 霍星亮, 张宝成. 近年来我国GNSS电离层延迟精确建模及修正研究进展[J]. 测绘学报, 2017, 46(10): 1 364-1 378 (Yuan Yunbin, Huo Xingliang, Zhang Baocheng. Research Progress of Precise Models and Correction for GNSS Ionospheric Delay in China over Recent Years[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1 364-1 378)
(  0) 0) |
| [2] |
刘长建. GNSS电离层建模方法与质量控制研究[D]. 郑州: 信息工程大学, 2011 (Liu Changjian. Study on Modeling Method and Model Quality Control of Ionosphere Based on GNSS[D]. Zhengzhou: Information Engineering University, 2011))
(  0) 0) |
| [3] |
张宝成, 欧吉坤, 李子申, 等. 利用精密单点定位求解电离层延迟[J]. 地球物理学报, 2011, 54(4): 950-957 (Zhang Baocheng, Ou Jikun, Li Zishen, et al. Determination of Ionospheric Observables with Precise Point Positioning[J]. Chinese Journal of Geophysics, 2011, 54(4): 950-957)
(  0) 0) |
| [4] |
李涌涛, 李建文, 魏绒绒, 等. 全球电离层TEC格网时空变化特性分析[J]. 武汉大学学报: 信息科学版, 2020, 45(5): 776-783 (Li Yongtao, Li Jianwen, Wei Rongrong, et al. Analysis of Temporal and Spatial Variation Characteristics of Global Ionospheric TEC Grid[J]. Geomatics and Information Science of Wuhan University, 2020, 45(5): 776-783)
(  0) 0) |
| [5] |
张小红, 任晓东, 吴风波, 等. 自回归移动平均模型的电离层总电子含量短期预报[J]. 测绘学报, 2014, 43(2): 118-124 (Zhang Xiaohong, Ren Xiaodong, Wu Fengbo, et al. Short-Term TEC Prediction of Ionosphere Based on ARIMA Model[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2): 118-124)
(  0) 0) |
| [6] |
Schaer S, Beutler G, Mervart L, et al. Global and Rionosphere Models Using the GPS Double Difference Phase Observable[C]. The IGS Workshop "Special Topics and New Directions", Postdam, 1996
(  0) 0) |
| [7] |
柳景斌, 王泽民, 章红平, 等. 几种地基GPS区域电离层TEC建模方法的比较及其一致性研究[J]. 武汉大学学报: 信息科学版, 2008, 33(5): 479-483 (Liu Jingbin, Wang Zemin, Zhang Hongping, et al. Comparison and Consistency Research of Regional Ionospheric TEC Models Based on GPS Measurements[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 479-483)
(  0) 0) |
| [8] |
鲁铁定, 黄佳伟, 贺小星, 等. EWT-Elman组合模型短期电离层TEC预报[J]. 大地测量与地球动力学, 2021, 41(7): 666-671 (Lu Tieding, Huang Jiawei, He Xiaoxing, et al. Short-Term Ionospheric TEC Prediction Using EWT-Elman Combination Model[J]. Journal of Geodesy and Geodynamics, 2021, 41(7): 666-671)
(  0) 0) |
| [9] |
Mallika I L, Ratnam D V, Ostuka Y, et al. Implementation of Hybrid Ionospheric TEC Forecasting Algorithm Using PCA-NN Method[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(1): 371-381 DOI:10.1109/JSTARS.2018.2877445
(  0) 0) |
| [10] |
汤俊, 钟正宇, 李垠健, 等. 基于SSA-Elman神经网络的电离层TEC短期预报模型[J]. 大地测量与地球动力学, 2022, 42(4): 378-383 (Tang Jun, Zhong Zhengyu, Li Yinjian, et al. Short-Term Prediction Model of Ionospheric TEC Based on SSA-Elman Neural Network[J]. Journal of Geodesy and Geodynamics, 2022, 42(4): 378-383)
(  0) 0) |
| [11] |
Çepni M S, Potts L V, Miima J B. High-Resolution Station-Based Diurnal Ionospheric Total Electron Content (TEC) from Dual-Frequency GPS Observations[J]. Space Weather, 2013, 11(9): 520-528 (  0) 0) |
| [12] |
Sun C Y, Sun Y, Xie K M. Mind-Evolution-Based Machine Learning and Applications[C]. The 3rd World Congress on Intelligent Control and Automation, IEEE, Hefei, 2000
(  0) 0) |
2. School of Social Science and Law, University of Bristol, 12 Priory Road, Bristol BS8 1TX, UK
 2023, Vol. 43
2023, Vol. 43

