2. 中国测绘科学研究院,北京市莲花池西路28号,100036;
3. 自然资源部,北京市阜成门内大街64号,100812
平均海面高是指在一定时段内海面相对于参考椭球面的平均高度,是研究垂直基准、海图基准和海平面变化的重要参考面,在海洋重力场、海洋大地水准面、海底地壳形变研究等方面发挥着重要作用。卫星测高极大地提高了海面高观测的时空分辨率和精度[1-2],利用卫星测高数据建立区域或全球平均海面高模型的研究也较多[3]。随着ERS、T/P等系列卫星的陆续发射,海面高度信息逐渐完善,模型的时空分辨率得到极大改善,WHU2013、CLS15、DTU18等一系列全球和区域平均海面高模型也相继建立[4]。
ERM数据具有较短的重复周期和较大的轨道间距,数据覆盖率较低,无法满足高分辨率格网数据密度的要求。而GM数据具有长周期、高覆盖率的特点,是建立高分辨率海面高模型必不可少的数据,但其不具备ERM数据周期性重复轨道的特点,无法通过共线平均的方法消除海面的时变影响。为消除时变影响,需对ERM数据进行共线处理。本文选择T/P系列卫星作为参考基准,利用与GM数据时间序列相对应的ERM轨道数据进行共线平均,得到对应时段的沿轨平均海面高,并通过插值来改正海洋时变对GM数据的影响。
目前较新的卫星高度计数据有HY-2A、Jason-3和Sentinel-3A,均未在CLS15和DTU18中使用。本文利用上述卫星观测数据建立平均海面高模型,通过与对应时段的T/P数据进行对比分析,验证HY-2A、Jason-3和Sentinel-3A对模型可靠性与准确性的改善效果。为使边缘数据在处理时获得更高的精度,将研究区域各向外扩展2°,即数据区域选择为7°~21°N、108°~118°E。
1 数据与方法 1.1 数据介绍由于使用的观测数据和处理方法不同,不同平均海面高模型(MSS)之间存在差异,WHU2013、CLS15和DTU18基准均为T/P、Jason-1和Jason-2的20 a(1993~2012年)平均剖面数据。WHU2013由武汉大学发布,使用1993~2012年多源卫星测高数据,其中ERM数据包括T/P、Jason-1、Jason-2、ERS-1、ERS-2、ENVISAT和GFO,GM数据包括ERS-1/168、Jason-1/GM和Cryosat-2/GM。由法国海洋和环境监测公司CLS和法国国家空间研究中心CNES联合发布的CLS15及由丹麦技术大学DTU发布的DTU18[5]均由时间跨度为1993~2012年的T/P、Jason-1、Jason-2、ERS-1、ERS-2、ENNVISAT、Geosat、GFO、Cryosat-2等测高卫星数据建立[6]。与CLS15相比,DTU18将GFO数据替换为SARAL/ERM数据,将ERS-1/168数据替换为SARAL/DP。本文将所建模型与CLS15、DTU18进行比较,以验证模型精度。
本文采用由Aviso发布的Level-2+版本海面高数据,数据已进行陆海识别,仅包含海洋表面,具有相同的数据格式。数据使用情况如表 1所示,不同卫星任务中包含不同参数,其中T/PA、Jason-1/A、Envisat/A为卫星变轨前的ERM数据,T/PB、Jason-1/B、Envisat/B为卫星变轨后的ERM数据。对各测高卫星进行地球物理与环境误差改正,包括电离层改正、对流层改正、潮汐改正、海况偏差改正、动态大气压改正等,物理环境改正后还需要根据Aviso提供的手册进行阈值筛选。
|
|
表 1 平均海面高模型使用数据 Tab. 1 Mean sea surface height model usage data |
由于CLS15、DTU18均基于T/P椭球,因此将所有卫星的参考椭球统一为T/P椭球。但不同卫星间仍存在系统差异,需利用四参数模型进行参考框架统一,公式如下:
| $\begin{gathered}H_{\text {obj }}=H_{\text {original }}+\Delta x \cos \varphi \cos \lambda+ \\ \Delta y \cos \varphi \sin \lambda+\Delta z \sin \varphi+B\end{gathered}$ | (1) |
式中,Hobj为需转换的目标框架,即T/P卫星参考框架的海面高;Horiginal为待转换的原始框架,即其他卫星参考框架的海面高;λ、φ为对应点的经、纬度;Δx、Δy、Δz为3个偏移量,B为整体偏移量。
本文以T/P系列卫星(T/P、Jason-1、Jason-2和Jason-3)变轨前的轨道(T/PA+Jason-1/A+Jason-2 +Jason-3)参考框架为基准,数据时段为1993-11~2018-12,将共线平均后的T/P系列卫星分别与不同卫星求取互交叉点,利用最小二乘法计算4个参数[7],参考框架转换参数见表 2(单位m)。
|
|
表 2 各测高卫星参考框架转换系数 Tab. 2 Reference frame conversion factor of each altimetry satellite |
ERM数据在一个重复周期内的重复轨迹理论上应该严格重合,但由于不同周期受力环境会发生变化,卫星重复轨迹并不能精准共线,而共线平均能够有效削弱海面高度的时变影响及由海洋异常造成的海面高异常现象[8]。首先确定参考轨迹,选取参与共线的重复周期观测数据中较为稳定、观测状况较好、观测数据较多的轨道,参考轨迹相邻采样点的间隔(即经纬度差或采样点时间间隔)应保持一致。本文选取各周期中采样点数量最多的轨道,当采样点空缺时,用相邻周期同纬度的海面高数据代替,从而获取一条连续稳定的参考轨迹。将其他周期的轨道观测数据内插至参考轨道,处理完所有周期数据后取平均值,获得长时间的平均海面高。具体计算过程如下:
1) 给定搜索条件,在弧段Cij上搜索出纬度φ0。可通过邻近2个观测点Ok(φk, λk)和Ok+1(φk+1, λk+1)的间隔时间Δt或者纬度差Δφ判定是否为有效观测点,本文采用纬度差Δφ进行判定。
2) 考虑到沿轨海平面变化较为平缓,相邻有效观测点可通过相似三角形原理线性内插得到O′的海面高:
| $\frac{h_{k+1}-h^{\prime}}{h_{k+1}-h_k}=\frac{d_{O^{\prime} O_{k+1}}}{d_{O_k O_{k+1}}}=\frac{\varphi_{k+1}-\varphi_0}{\varphi_{k+1}-\varphi_k}$ | (2) |
| $h^{\prime}=h_{k+1}-\frac{\varphi_{k+1}-\varphi_0}{\varphi_{k+1}-\varphi_k}\left(h_{k+1}-h_k\right)$ | (3) |
式中,dO′Ok+1和dOkOk+1分别为Ok+1到O′和Ok的距离。将计算得到的内插点的海面高h′(即O′的海面高)与参考点O的海面高求平均。
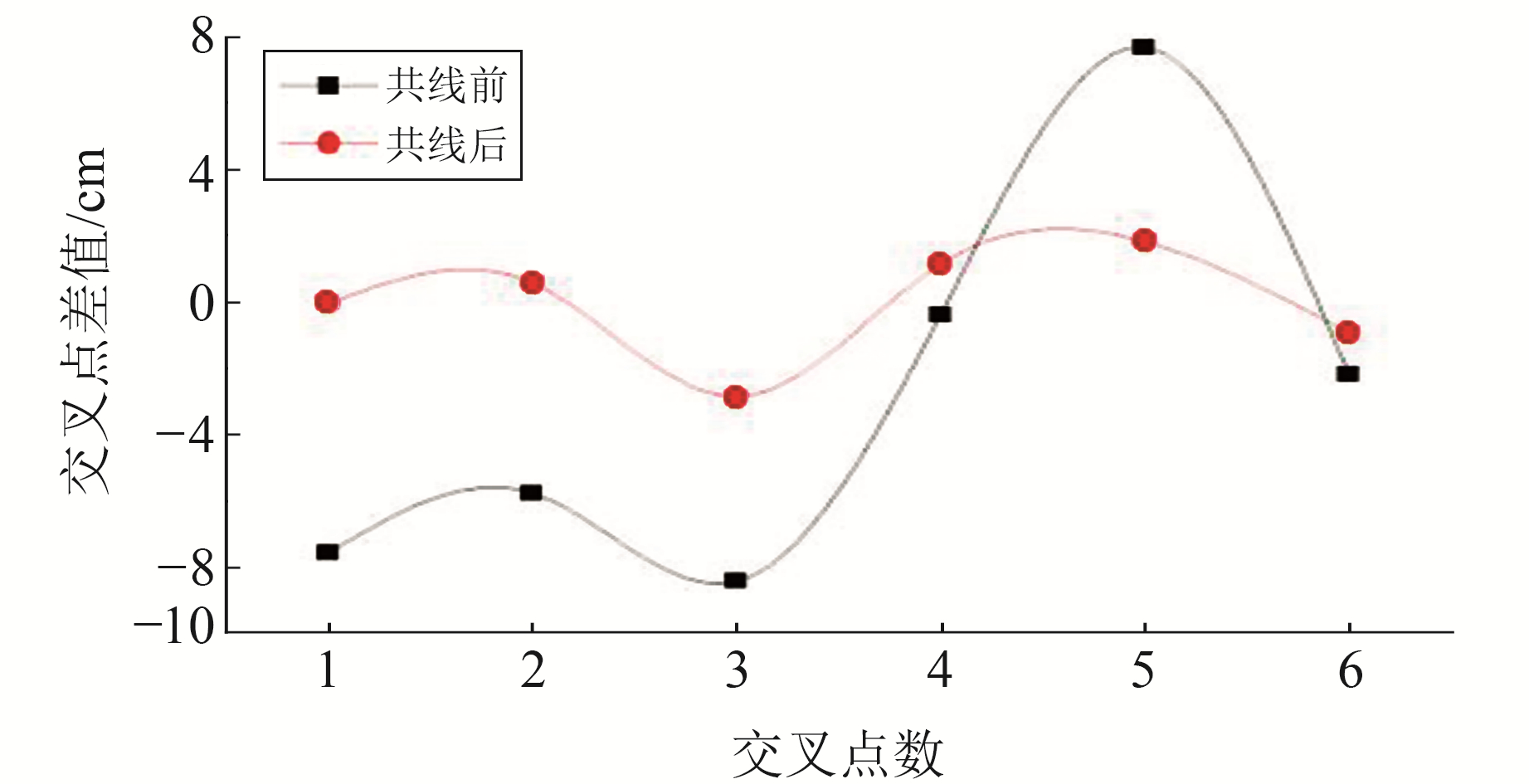
各卫星ERM数据共线平均前的均方根RMS、标准差STD平均值分别为13.81 cm、13.79 cm;共线平均后的RMS、STD平均值分别为4.37 cm、4.31 cm,由此可知共线平均削弱了大部分的时变影响。图 1为T/P系列卫星(包括T/P、Jason-1、Jason-2、Jason-3)共线平均前后的交叉点不符值。
|
图 1 T/P系列卫星共线平均前后的交叉点不符值 Fig. 1 Intersection discrepancies before and after collinear analysis of T/P series satellites |
ERM数据具有周期性特征,能通过共线平均削弱时变影响,因此利用共线后的ERM数据可有效校正海面时变影响,且共线平均后轨道精度能够得到较大幅度的提升。T/P系列卫星数据的测量精度最高,因此本文首先选取1992~2018年连续T/PA、Jason1/A、Jason-2和Jason-3卫星高度计数据,经共线平均后作为参考轨迹;然后计算与GM时间区间相对应的T/P系列数据的海面高度异常值(SLA)(表 3);最后利用反距离加权平均法插值出高度改正量。
|
|
表 3 GM数据对应T/P系列的周期和时间 Tab. 3 GM data corresponds to the cycle and time of T/P series |
对于所有卫星,改正前交叉点不符值的最大值、最小值分别为66.65 cm、-84.08 cm,mean、RMS、STD分别为0.22 cm、13.21 cm、13.19 cm;改正后的最大值、最小值分别为57.68 cm、-76.78 cm,mean、RMS、STD分别为0.06 cm、11.68 cm、11.68 cm,差值分布于±10 cm以内的占比从57.32%提升至63.64%。各卫星经过时变改正后的mean、RMS、STD均有显著提高。
1.5 交叉点平差经过各项改正及海面时变影响削弱后的测高卫星数据的单星交叉点不符值仍达到数个甚至十几个cm量级,除包含一些系统偏差项外,还包含径向轨道误差,而交叉点平差是削弱径向轨道误差最有效的方法之一。平差时采取的是验后补偿法[9]:剔除不符值大于50 cm的点,交叉点平差前后其自交叉点不符值的mean、RMS、STD见表 4(单位cm,剔除比例为剔除点数/总点数)。
|
|
表 4 单星自交叉点平差前后统计 Tab. 4 Statistical of ERM data before and after self-crossover adjustment |
以TP/A(1993~2002年)、Jason-1/A(2002~2008年)、Jason-2(2008~2016年)、Jason-3(2016~2018年)共线后的轨迹为基准,平差前后的交叉点不符值情况见表 5(单位cm)。
|
|
表 5 多星互交叉点平差后交叉点不符值统计 Tab. 5 Cross point difference statistics after multi-star crossover adjustment |
各测高卫星ERM数据互交叉点平差前的STD平均值为4.06 cm,平差后降为3.33 cm;GM数据互交叉点平差前的STD平均值为7.90 cm,平差后降为5.29 cm。由此可知,轨道精度得到有效提高。
1.6 建立海面高模型海洋潮汐模型通常被用来削弱周期性潮汐信号,其准确性对高度计数据的质量有较大影响[10-11]。海洋潮汐具有周期性变化,包括1 d周期、1.5 d周期、1个月周期、1.5个月周期、1 a周期、8.85 a周期和18.61 a周期等。本文选择用19 a滑动平均法,通过平均消除部分周期性海洋潮汐对模型的影响。具体方法为:首先将1992~2018年的卫星数据以19 a为单位滑动分组,根据每组数据分别建立1′×1′格网的平均海面高模型;然后将8组格网求平均值:
| $\begin{gathered}\operatorname{MSS}h_i= \\ \left(\mathrm{MSS}h_{i, 1}+\operatorname{MSS}h_{i, 2}+\cdots+\operatorname{MSS}h_{i, 8}\right) / 8\end{gathered}$ | (4) |
式中,MSShi为本文建立模型的网格点i处的平均海面高,MSShi, j(j=1, …, 8)为第j组的网格点i处的平均海面高。
本文采用连续曲率张力样条法确定研究区域平均海面高[12]。图 2为最终模型,研究区域呈西北低东南高的特点,最低点海面高约8 m,最高点约40 m,高度由西北向东南逐渐增加。

|
图 2 平均海面高模型 Fig. 2 Mean sea height model |
为检验模型精度,通过模型之间和独立于模型的测高数据对比来验证可靠性和准确性[13]。本文利用CLS15、DTU18和独立于模型的卫星数据(Sentinel-3B、HY-2B)验证模型精度,建立MSS时使用未在CLS15与DTU18中使用过的HY-2A、Jason-3和Sentinel-3A三颗卫星的数据,并对模型精度的提升效果进行分析。
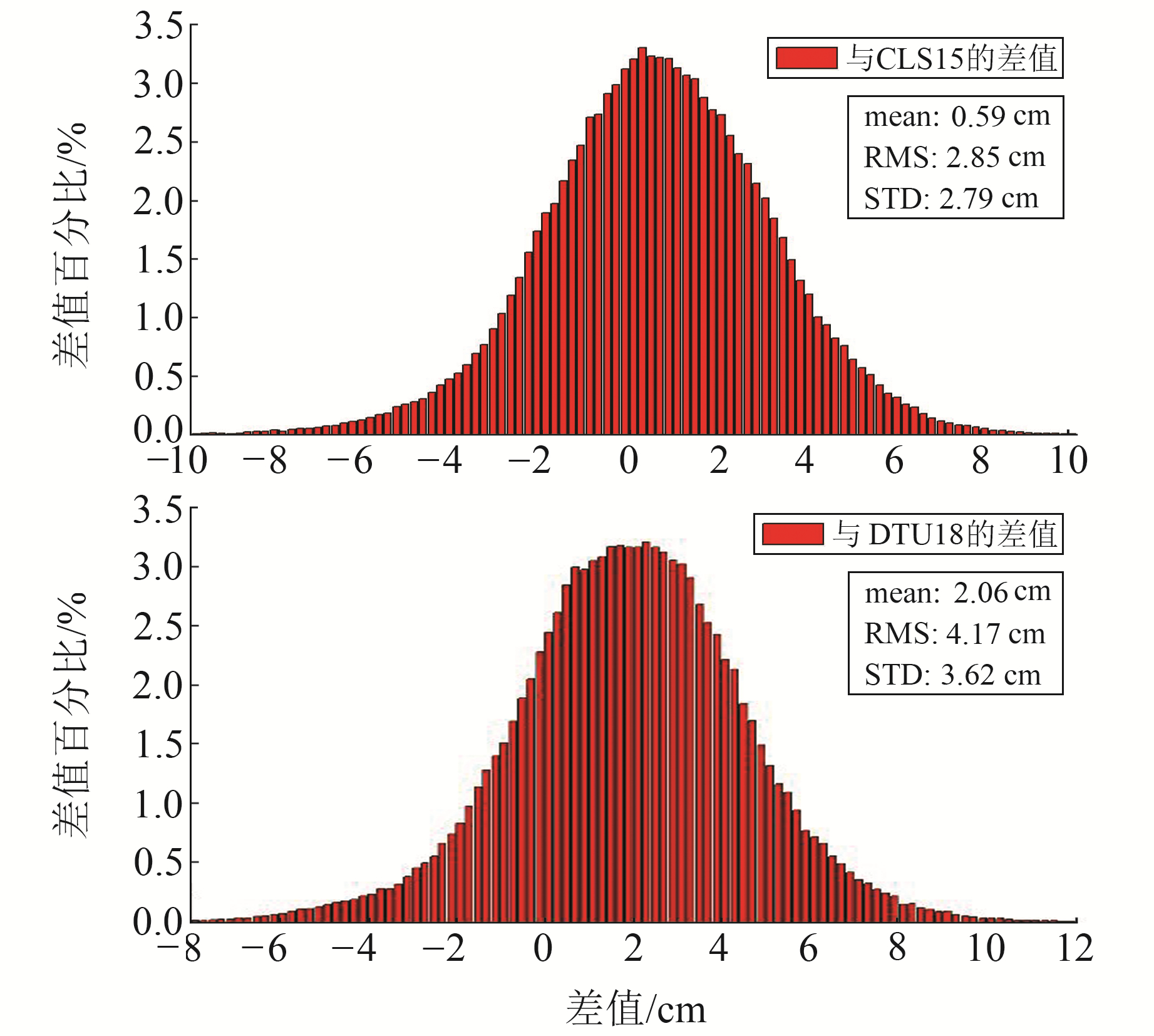
2.1 模型验证本文模型与CLS15、DTU18之间的差值统计见表 6(单位cm),同时建立格网点差值的频率分布直方图(图 3)。可以看出,本文模型与CLS15的差值主要集中在-8~8 cm,均小于10 cm,与DTU18的差距主要集中在-6~10 cm,平均值存在近2 cm的偏差,说明本文模型与CLS15的差值更符合正态分布,2个模型更为相近。本文模型与CLS15、DTU18的STD分别为2.79 cm和3.62 cm,均小于CLS15与DTU18之间差值的STD,证明本文所建模型可靠。
|
|
表 6 不同模型间的差异 Tab. 6 Differences between different models |
|
图 3 模型与CLS15、DTU18 MSS格网点差值 Fig. 3 Difference between the model and CLS15, DTU18 MSS grid points |
模型与测高数据的比较不仅能够表现出MSS插值过程的准确度,还能体现模型精度,即相差的STD越小,MSS越准确[14]。本文选用T/P系列卫星经过共线平均后的轨迹(T/PA+Jason-1/A+Jason-2+Jason-3)、Sentinel-3B及HY-2B三种数据(均为ERM数据)来验证模型精度。首先对Sentinel-3B和HY-2B数据进行预处理(物理环境改正、参考椭球及参考框架转换)和共线平均,然后将不同MSS格网点沿实测轨道点进行经纬度插值,通过统计二者海面高差值分析所建模型的可靠性,结果见表 7(单位cm)。由表可见,本文模型与CLS15、DTU18之间差异较小,STD的最大差值为0.72 cm,这是由于本文使用的卫星数据时段与CLS15(DTU18)存在近7 a的差异,这也说明本文所建模型与参考轨迹(T/P) 之间的差异更小。Sentinel-3B和HY-2B卫星中3种模型之间的STD最大差值为0.62 cm,其中Sentinel-3B卫星中本文模型的STD小于CLS15与DTU18,可能是因为使用数据的时间与本文建立模型的时间更为接近。表 6和7反映了模型间良好的一致性。
|
|
表 7 模型与沿轨数据不符值的STD Tab. 7 STD of the difference between the model and the data along the track |
Jason-3作为Jason-2的延续卫星,延长了参考轨迹的时间范围,增加了参考轨道观测数据,而HY-2A ERM、HY-2A GM和Sentinel-3A ERM数对区域轨道覆盖率和模型精度的影响分析如下:
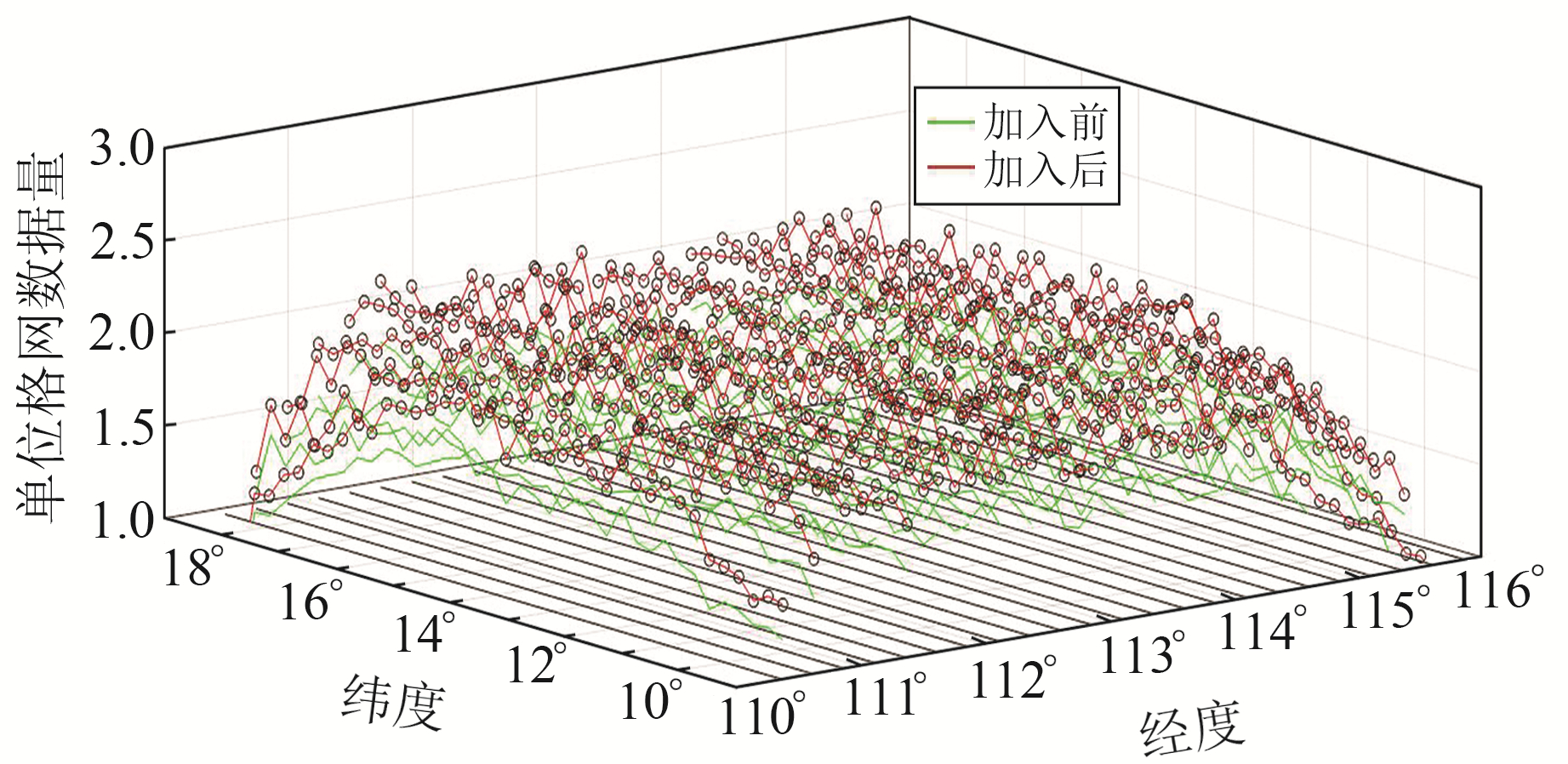
首先将数据分为2组,一组不包含HY-2A ERM、HY-2A GM和Sentinel-3A ERM数,记为GroupA;另一组包含,记为GroupB,GroupA和GroupB的观测点数分别为507 006个和603 946个。以指定范围内(0.25°×0.25°)单位格网(1′×1′)的数据量作为轨道覆盖率的评判标准,2组模型的轨道覆盖率见图 4。GroupA的max、min、mean分别为1.82 cm、0.53 cm、1.59 cm,GroupB的max、min、mean分别为2.23 cm、0.6 cm、1.88 cm。对于轨道覆盖率较低的区域(9°~10°N,110°~111°E),单位格网数据量由1.08提升至1.2。由此可知,加入新卫星数据后,提高了轨道覆盖率。
|
图 4 数据加入前后轨道覆盖率变化 Fig. 4 Track coverage changes before and after data addition |
根据滑动平均法列出的8个MSS,筛选出每组同期T/P系列卫星数据(表 8)。由于缺少足够数量的数据对模型进行绝对验证,本文利用共线平均后的高精度卫星数据(T/P系列)作为参考轨迹,通过对比同期模型与参考轨迹的不符值得出结论,统计结果见表 9(单位cm),表中Grid1为表 8 Group1建立的分辨率为1′×1′的MSS。
|
|
表 8 每组模型对应T/P系列的周期和时间 Tab. 8 The period and time of each group of models corresponding to the T/P series |
|
|
表 9 每组模型与参考轨迹不符值的统计量 Tab. 9 Statistics of the difference between each set of models and the reference trajectory |
由表 9可见,平均值可能存在一定的系统偏差,原因可能是构建的模型依赖于GM数据的数量与质量,而GM数据的时效改正只能消除部分海平面变化,且与ERM数据的共线平均效果有着一定的差距。Grid1与参考轨迹的差异最大,原因可能是Group1中仅包含ERS-1/168及Cryosat-2/GM的10个周期(14~24)数据,卫星轨道覆盖密度与数据量及卫星的测量精度可能是影响格网精度的主要原因。Grid1~4的STD随Cryosat-2/GM与Jason-1/GM数据量的增加而减小,其中Cryosat-2/GM为主要因素。Grid4~5没有新的测高数据加入,STD保持稳定,但Grid6中加入了24个周期的HY-2A/GM,模型精度也随之提升。Grid7中加入了23个周期(2~24)的Sentinel-3A和SARAL/DP数据,而Grid8中没有加入新的卫星数据,STD也保持稳定。这说明,随着新老卫星的更替,与参考轨迹不符值的STD也随之减小,模型精度在逐步提高。
3 结语本文利用多源卫星高度计数据,采用19 a滑动平均法建立研究区域(9°~19°N,110°~116°E)1993~2018年平均海面高模型,并利用CLS15、DTU18和测高数据验证模型精度。对比每组模型与参考轨迹的不符值后发现,随着新一代卫星的加入,模型的精度也随之提升。对于高分辨率海面高模型而言,在数据充足的情况下,GM数据的加入才是改善模型精度的关键;而ERM数据的影响较小,进一步消除海面时变GM数据的影响最为关键。
| [1] |
褚永海, 李建成. 联合全球重力场模型和海面高模型确定平均海面位常数[J]. 大地测量与地球动力学, 2012, 32(5): 58-62 (Chu Yonghai, Li Jiancheng. Determination of Mean Sea Level Geotential from Global Gravity Field Model and Global Sea Surface Height Model[J]. Journal of Geodesy and Geodynamics, 2012, 32(5): 58-62)
(  0) 0) |
| [2] |
Cipollini P, Calafat F M, Jevrejeva S, et al. Monitoring Sea Level in the Coastal Zone with Satellite Altimetry and Tide Gauges[J]. Surveys in Geophysics, 2017, 38(1): 33-57 DOI:10.1007/s10712-016-9392-0
(  0) 0) |
| [3] |
Basic T, Rapp R H. Oceanwide Prediction of Gravity Anomalies and Sea Surface Heights Using Geos-3, Seasat, and Geosat Altimeter Data and ETOPO5U Bathymetric Data[J]. Geophysical Research Letter, 1992, 19(19): 1 979-1 982 DOI:10.1029/92GL02247
(  0) 0) |
| [4] |
金涛勇, 李建成, 姜卫平, 等. 基于多源卫星测高数据的新一代全球平均海面高模型[J]. 测绘学报, 2011, 40(6): 723-729 (Jin Taoyong, Li Jiancheng, Jiang Weiping, et al. The New Generation of Global Mean Sea Surface Height Model Based on Multi-Altimetric Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 723-729)
(  0) 0) |
| [5] |
Andersen O, Knudsen P, Stenseng L. A New DTU18 MSS Mean Sea Surface-Improvement from SAR Altimetry[C]. 25 Years of Progress in Radar Altimetry Symposium, Roma, 2018
(  0) 0) |
| [6] |
Jin T Y, Li J C, Jiang W P. The Global Mean Sea Surface Model WHU2013[J]. Geodesy and Geodynamics, 2016, 7(3): 202-209 DOI:10.1016/j.geog.2016.04.006
(  0) 0) |
| [7] |
张胜军. 基于多星测高数据的中国近海及邻域平均海平面模型建立及应用研究[D]. 青岛: 中国石油大学(华东), 2012 (Zhang Shengjun. Mean Sea Surface Model Creation and Application Research over China Sea and Its Vicinity Area Derived from Multi-Satellites Altimeter[D]. Qingdao: China University of Petroleum, 2012)
(  0) 0) |
| [8] |
文汉江, 金涛勇, 朱广彬, 等. 卫星测高原理及应用[M]. 北京: 测绘出版社, 2017 (Wen Hanjiang, Jin Taoyong, Zhu Guangbin, et al. Principle and Application of Satellite Altimetry[M]. Beijing: Surveying and Mapping Press, 2017)
(  0) 0) |
| [9] |
张倩. 卫星测高数据交叉点处理方法研究[D]. 青岛: 中国石油大学(华东), 2015 (Zhang Qian. Research on the Processing Methods of the Crosspoints of Satellite Altimeter Data[D]. Qingdao: China University of Petroleum, 2015)
(  0) 0) |
| [10] |
Yuan J J, Guo J Y, Liu X, et al. Mean Sea Surface Model over China Seas and Its Adjacent Ocean Established with the 19-Year Moving Average Method from Multi-Satellite Altimeter Data[J]. Continental Shelf Research, 2020, 192
(  0) 0) |
| [11] |
倪清, 褚永海. 连续曲率张力样条方法在测高数据格网化中的应用[J]. 测绘地理信息, 2016, 41(2): 26-28 (Ni Qing, Chu Yonghai. Continuous Curvature Splines in Tension Applied for Gridding Satellite Altimetry Data[J]. Journal of Geomatics, 2016, 41(2): 26-28)
(  0) 0) |
| [12] |
Cancet M, Andersen O B, Lyard F, et al. Arctide2017, A High-Resolution Regional Tidal Model in the Arctic Ocean[J]. Advances in Space Research, 2018, 62(6): 1 324-1 343 DOI:10.1016/j.asr.2018.01.007
(  0) 0) |
| [13] |
牛余朋. 基于卫星测高、验潮和GNSS的日本海及邻近海域海面高模型建立及海平面变化预测[D]. 青岛: 山东科技大学, 2020 (Niu Yupeng. Establishment of Mean Sea Surface Models and Prediction of Sea Level Changes over Sea of Japan and Its Adjacent Ocean Based on Satellite Altimetry, Tide Gauge and GNSS[D]. Qingdao: Shandong University of Science and Technology, 2020)
(  0) 0) |
| [14] |
Andersen O B, Knudsen P. DNSC08 Mean Sea Surface and Mean Dynamic Topography Models[J]. Journal of Geophysical Research Atmospheres, 2009, 114(C11)
(  0) 0) |
2. Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road, Beijing 100036, China;
3. Ministry of Natural Resources, 64 Fuchengmennei Street, Beijing 100812, China
 2023, Vol. 43
2023, Vol. 43


