2. 自然资源部大地测量数据处理中心,西安市友谊东路334号,710054
GPS坐标时间序列的长期观测分析对于大地测量和地球物理解释至关重要[1]。动力学和变形模式的最小二乘估计需要无阶跃观测,以提供无偏参数和不确定性,未建模的阶跃可能导致模型的估计结果有偏或速度估计不可靠。对长期GPS坐标时间序列而言,阶跃量可能会严重影响台站速度的估计[2]。因此,面对海量的GPS连续站数据,阶跃的自动探测和估计是GPS坐标时间序列管理的重点。Chen等[3]提出一种随机水平位移模型来探测未知阶跃,但只能探测出较大幅度的阶跃;Williams[1]提出一种使用变化探测的阶跃探测算法,可用于探测小幅度的阶跃,但该算法基于序列误差项中只有白噪声的假设,忽略了有色噪声的存在[4-7];Perfetti[8]成功探测出意大利GPS基准网现有坐标时间序列70%的已知阶跃;Gazeaux等[9]设计联合分割程序,同步估计相邻GPS站的趋势、季节信号和阶跃量,利用空间的冗余性来探测可能的阶跃,但该方法容易过度分割;Khazraei等[10]提出一种使用多变量分析探测阶跃的方法,利用改进的样条函数算法提升探测性能;Tehranchi等[11]使用基于最大重叠离散小波变换(MODWT)的多分辨率分析(MRA) 探测可能的阶跃,该变换适用于对局部时频变化的跟踪。
奇异谱分析(SSA)作为一种数字信号处理技术,具有无需任何先验信息和假设条件、无需建模、无需考虑噪声等特征,可以从物理本质未知的数据中提取尽可能多的可靠信息,用于趋势识别、周期判断、降噪处理和数据重构等。基于上述分析,本文提出基于SSA的GPS坐标时间序列阶跃探测,并通过真实数据测试其探测效果。
1 方法 1.1 奇异谱分析对于原始GPS坐标时间序列{x1, x2, x3, …, xN},首先选择窗口M(M < N/2)构建M×(N-M+1)维时间滞后矩阵X:
| $ \boldsymbol{X}=\left[\begin{array}{cccc} x_1 & x_2 & \cdots & x_{N-M+1} \\ x_2 & x_3 & \cdots & x_{N-M+2} \\ \vdots & \vdots & \vdots & \vdots \\ x_M & x_{M+1} & \cdots & x_N \end{array}\right] $ | (1) |
然后,求出滞后矩阵X的自协方差矩阵C=XTX,并对其进行奇异值分解:
| $ \boldsymbol{C}=\boldsymbol{V} \boldsymbol{\varLambda} \boldsymbol{V}^{\mathrm{T}} $ | (2) |
式中,Λ为对角阵,表示特征值λ1≥λ2≥…λM≥0;V为正交阵,表示特征向量Vk, j;时间主成分矩阵A = VX,表示滞后序列X在特征向量Vk, j上的投影,A的第k列为第k个主成分:
| $\begin{gathered} a_{i k}=\sum\limits_{j=1}^M x_{i+j} \boldsymbol{V}_{k, j}, \\ 0 \leqslant i \leqslant N-M, 1 \leqslant j \leqslant M \end{gathered} $ | (3) |
最后进行时间序列的重建,由第k个时间主成分和特征向量按照式(4)重建第k个分量xik。选取前k个贡献率大的成分合并,重建时间序列:
| $ x_i^k=\left\{\begin{array}{l} \frac{1}{i} \sum\limits_{j=1}^i a_{i-j+1, k} \boldsymbol{V}_{k, j}, \\ 1 \leqslant i \leqslant M-1 \\ \frac{1}{M} \sum\limits_{j=1}^M a_{i-j+1, k} \boldsymbol{V}_{k, j}, \\ M \leqslant i \leqslant N-M+1 \\ \frac{1}{N-i+1} \sum\limits_{j=i-N+M}^M a_{i-j+1, k} \boldsymbol{V}_{k, j}, \\ N-M+2 \leqslant i \leqslant N \end{array}\right. $ | (4) |
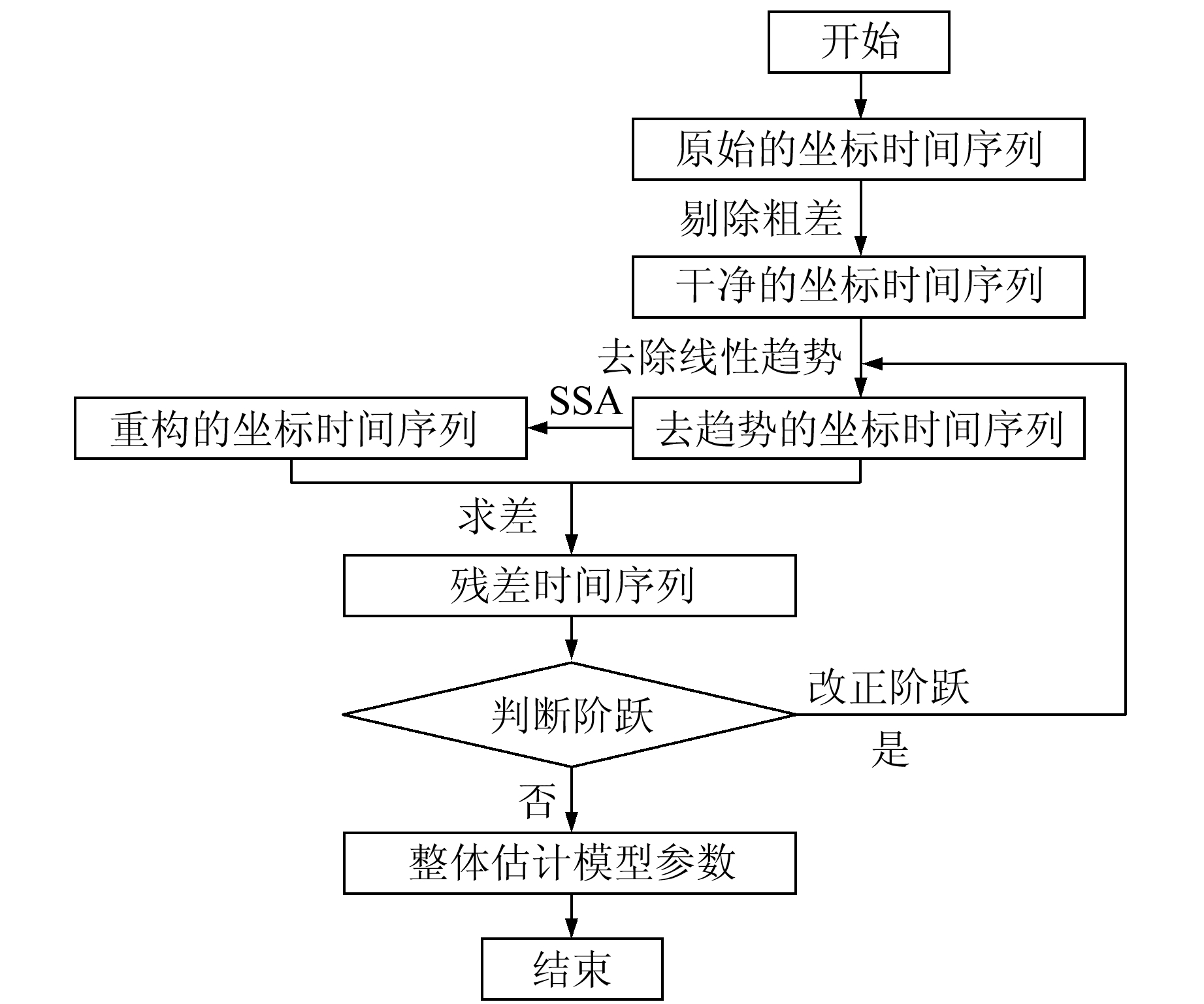
基于SSA探测阶跃的思路是:利用SSA计算坐标时间序列,趋势长和重复性高的信号贡献占比更高,随机的阶跃信号贡献小。因此,SSA提取出的主要成分为趋势长和重复性高的形变信号,扣除主要成分重构的时间序列后得到残差时间序列,可以凸显阶跃信号,更容易被探测和识别。具体步骤如下(图 1):
|
图 1 自动探测阶跃流程 Fig. 1 The flowchart of automatic detecting the offset |
1) 线性拟合粗略估计时间序列的线性趋势,扣除线性趋势项,凸显其他信号(阶跃会影响趋势项的估计,粗略扣除趋势项仅为凸显其他信号强度,不影响阶跃探测)。
2) 对去趋势项后的时间序列进行去均值和标准化,构建滞后矩阵,进行SSA计算,得到各主成分序列,根据特征值选取主要成分重建时间序列。
3) 将去趋势项的时间序列与重建的时间序列作差得到残差时间序列,对残差时间序列逐历元判断是否存在阶跃。判断原则为:①该历元前2周和后2周的残差时间序列分别位于中位数的两端,防止个别粗差影响导致漏判,允许2个历元的残差值不符合该原则;②该历元前1周和后1周残差时间序列的平均值坐标差超过2倍基准值时判定为阶跃,基准值设定为整个残差时间序列的上下四分位之差。
4) 识别并改正所有阶跃,重复步骤1)~3),判断是否存在遗漏的阶跃。若不存在,退出循环;否则继续重复步骤1)~3)。
2 算例为调查探测阶跃的效果,以加州连续GPS观测网络CAND站和ALBH站为例进行实验,坐标时间序列数据来源于SOPAC。CAND站受到2003年San Simeon和2004年Parkfield地震的同震影响,产生了2次较大的同震阶跃,同时具有明显的震后形变现象;ALBH站存在3次小幅阶跃。
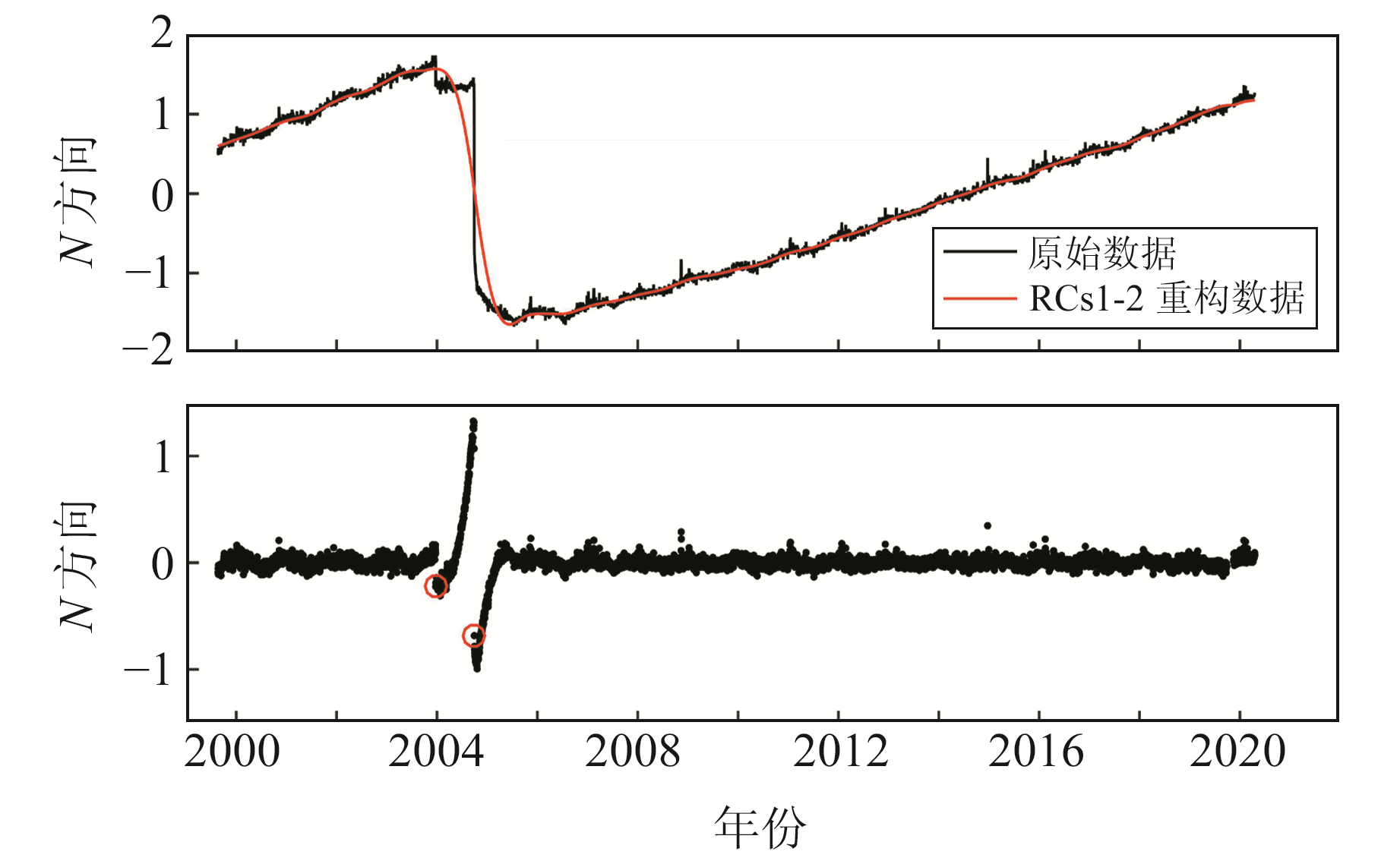
由图 2可见,以N方向为例,从CAND站去趋势后的坐标时间序列可以明显看出2次地震产生的阶跃和震后形变,对该坐标时间序列进行SSA计算,根据前2个主成分重构坐标时间序列,对标准化的坐标时间序列和重构的坐标时间序列作差得到残差坐标时间序列。此时,周期、震后形变等信号被大幅抑制。判定出的阶跃位置与该站坐标时间序列头文件给出的阶跃位置一致,说明本文方法不受震后形变等瞬态形变的干扰,可以准确判定出阶跃位置。
|
图 2 CAND站标准化和重构的坐标时间序列及阶跃位置 Fig. 2 Normalized and reconstructed coordinatetime series of CAND station and the automatic detected offsets |
由图 3(红线为标注的阶跃位置,红圈为自动识别的阶跃位置)可见,以U方向为例,ALBH站时间序列存在3个阶跃,分别为1 994.283 6、1 995.028 8、2 003.689 0历元。1 994.283 6和2 003.689 0历元的阶跃被成功探测,2 003.689 0历元的阶跃被探测为2 003.680 8历元,提前了3 d。从时间序列来看,本文探测的历元更准确,自动识别方法可以帮助避免一些人工疏漏。1 995.028 8历元的阶跃混入背景运动,无法观测到明显台阶,本文方法没有探测出该阶跃,说明本文方法存在一定的局限性,对于不存在明显台阶的阶跃不敏感,需要管理者记录好仪器更换、维护、干扰等情况,避免阶跃的遗漏。

|
图 3 标准化的残差时间序列和阶跃 Fig. 3 Normalized residual time series and offsets |
测试SOPAC的坐标时间序列发现,50个GNSS坐标时间序列中包含29个阶跃,其中28个站的自动探测结果与头文件一致,探测准确性为56%。进一步从3个维度进行统计分析:真阳性TP定义为检测到真阶跃;假阳性FP定义为检测到不存在的阶跃,为误报;假阴性FN定义为未检测到真阶跃,为漏报。经统计,本文方法的TP、FN、FP分别为26.2%、42.6%、31.2%。
Gazeaux等[2]通过模拟50个站的坐标时间序列,比较8种探测阶跃方法和5种人工筛查结果,并从TP、FN、FP 3个维度来衡量检测效果。结果表明,人工筛查的FP较低、FN较高,而自动探测方法的FP和FN差异较大。Khazraei等[10]和Tehranchi等[11]分别计算了ASMULTI和WR探测方法的TP、FN、FP,表 1(单位%)为上述方法与本文方法的对比结果,由表可见,本文方法与AIUBCOD2、ASMULTI2和WR方法的误报率相当,但漏报率略高,较GA和MR更均衡。需要说明的是,对比方法采用的是模拟数据,数据质量略好于真实数据,而真实数据的阶跃更少,计算出的TP可能偏低。此外,模拟数据的阶跃已知,而本文方法采用实测数据,假定人工探测的阶跃为真实阶跃,两者的计算结果存在一定的差异。
|
|
表 1 不同阶跃探测方法的对比 Tab. 1 Comparison of different offset detection |
分析可知,SSA方法探测GPS坐标时间序列的阶跃幅度越大,自动识别的有效性就越高。本文开展进一步实验来讨论该方法的探测极限:ALBH站U方向上的坐标时间序列标准差为7.78 mm,将阶跃量分别设定为7.78 mm、3.89 mm和2.33 mm(1、0.5和0.3倍标准差)进行测试发现,以上阶跃均可被准确探测。设定阈值为1.76 mm(2倍标准差)的基准值,结果表明,超过阈值的阶跃可以被探测。由此可知,阈值是自动识别的关键因素:一方面,阈值的基准值为整个残差时间序列的上下四分位之差,与数据质量直接相关;另一方面,阈值的倍数起到调节作用,阈值越高,探测的误报率越低,可能存在漏报;阈值越低,探测的阶跃越多,可能存在虚测。
3 结语本文基于SSA方法进行GPS坐标时间序列的阶跃探测,为自动探测阶跃提供新思路。该方法可以探测出有明显台阶的阶跃,且震后形变等瞬态运动不影响探测结果,但对于与背景运动差异不明显的阶跃探测存在一定的局限性,还有待进一步完善。
| [1] |
Williams S D P. The Effect of Coloured Noise on the Uncertainties of Rates Estimated from Geodetic Time Series[J]. Journal of Geodesy, 2003, 76(9-10): 483-494 DOI:10.1007/s00190-002-0283-4
(  0) 0) |
| [2] |
Gazeaux J, Williams S, King M, et al. Detecting Offsets in GPS Time Series: First Results from the Detection of Offsets in GPS Experiment[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(5): 2 397-2 407 DOI:10.1002/jgrb.50152
(  0) 0) |
| [3] |
Chen C, Tiao G C. Random Level-Shift Time Series Models, ARIMA Approximations, and Level-Shift Detection[J]. Journal of Business and Economic Statistics, 1990, 8(1): 83-97
(  0) 0) |
| [4] |
Zhang J, Bock Y, Johnson H, et al. Southern California Permanent GPS Geodetic Array: Error Analysis of Daily Position Estimates and Site Velocities[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B8): 18 035-18 055 DOI:10.1029/97JB01380
(  0) 0) |
| [5] |
Williams S D P, Bock Y, Fang P, et al. Error Analysis of Continuous GPS Position Time Series[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B3)
(  0) 0) |
| [6] |
Amiri-Simkooei A R, Tiberius C C J M, Teunissen P J G. Assessment of Noise in GPS Coordinate Time Series: Methodology and Results[J]. Journal of Geophysical Research: Solid Earth, 2007, 112(B7)
(  0) 0) |
| [7] |
Khodabandeh A, Amiri-Simkooei A R, Sharifi M A. GPS Position Time-Series Analysis Based on Asymptotic Normality of M-Estimation[J]. Journal of Geodesy, 2012, 86(1): 15-33 DOI:10.1007/s00190-011-0489-4
(  0) 0) |
| [8] |
Perfetti N. Detection of Station Coordinate Discontinuities within the Italian GPS Fiducial Network[J]. Journal of Geodesy, 2006, 80(7): 381-396 DOI:10.1007/s00190-006-0080-6
(  0) 0) |
| [9] |
Gazeaux J, Lebarbier E, Collilieux X, et al. Joint Segmentation of Multiple GPS Coordinate Series[J]. Journal de la Société Française de Statistique, 2015, 156(4): 163-179
(  0) 0) |
| [10] |
Khazraei S M, Amiri-Simkooei A R. Improving Offset Detection Algorithm of GNSS Position Time-Series Using Spline Function Theory[J]. Geophysical Journal International, 2020, 224(1): 257-270 DOI:10.1093/gji/ggaa453
(  0) 0) |
| [11] |
Tehranchi R, Moghtased-Azar K, Safari A. A New Statistical Test Based on the WR for Detecting Offsets in GPS Experiment[J]. Earth and Space Science, 2020(7)
(  0) 0) |
2. Geodetic Data Processing Center, MNR, 334 East-Youyi Road, Xi'an 710054, China
 2023, Vol. 43
2023, Vol. 43

