2. 中石化石油工程地球物理有限公司胜利分公司,山东省东营市镇前街173号,257100;
3. 青岛北斗陆海科技有限公司,青岛市江山南路480号,266555
单系统定位时因观测卫星较少会导致定位结果稳定性较差,而多系统组合定位可通过增加观测卫星数来改善卫星空间几何结构,提高定位精度和稳定性。
目前基于多系统组合的相对定位研究主要集中于采用3个频率以内的信号[1-8],而随着BDS-3和Galileo卫星系统均可提供四频信号,且长基线定位技术在地壳形变监测和时间同步等领域的作用愈发重要,对长基线场景下多频信号的多系统组合定位进行研究具有重要意义。考虑到超宽巷或宽巷模糊度较原始窄巷模糊度具有更易固定的特点,当前已经有部分学者利用BDS三频数据对宽巷模糊度解算的定位精度进行分析验证,并得到良好的定位效果[9-12],可见,采用模糊度固定后的宽巷组合直接进行单历元定位具有可行性。本文首先根据总噪声水平最小原则对BDS-3和Galileo四频宽巷组合进行优选,然后基于优选的四频宽巷组合构建BDS-3和Galileo单系统、BDS-3/Galileo双系统组合定位方程,并给出加入GPS双频宽巷组合观测值后的三系统组合定位方程,最后通过采用IGS提供的多频数据进行实验,对多系统组合定位的长基线相对定位精度及稳定性进行对比分析。
1 多频GNSS观测模型假设多频组合系数为i1、i2、…、ik,其中k为频数,则多频双差伪距与相位观测方程可表示为[13]:
| $ \begin{gathered} \nabla \Delta P_{\left(i_1, i_2, \cdots, i_k\right)}=\nabla \Delta \rho+\nabla \Delta T+\beta_{\left(i_1, i_2, \cdots, i_k\right)} \nabla \Delta I_1+ \\ \theta_{\left(i_1, i_2, \cdots, i_k\right)} \nabla \Delta I_2+\varepsilon_{\nabla \Delta P\left(i_1, i_2, \cdots, i_k\right)} \end{gathered} $ | (1) |
| $ \begin{gathered} \nabla \Delta \varPhi_{\left(i_1, i_2, \cdots, i_k\right)}=\nabla \Delta \rho+\nabla \Delta T-\beta_{\left(i_1, i_2, \cdots, i_k\right)} \nabla \Delta I_1- \\ \theta_{\left(i_1, i_2, \cdots, i_k\right)} \nabla \Delta I_2- \\ \lambda_{\left(i_1, i_2, \cdots, i_k\right)} \nabla \Delta N_{\left(i_1, i_2, \cdots, i_k\right)}+\varepsilon_{\nabla \Delta \varPhi\left(i_1, i_2, \cdots, i_k\right)} \end{gathered} $ | (2) |
式中,
根据单个频点上的原始观测值,式(1)和式(2)可进一步展开为式(3)和式(4):
| $ \nabla \Delta P_{\left(i_1, i_2, \cdots, i_k\right)}=\frac{i_1 f_1 \nabla \Delta P_1+i_2 f_2 \nabla \Delta P_2+\cdots+i_k f_k \nabla \Delta P_k}{i_1 f_1+i_2 f_1+\cdots+i_k f_k} $ | (3) |
| $ \nabla \Delta \varPhi_{\left(i_1, i_2, \cdots, i_k\right)}=\frac{i_1 f_1 \nabla \Delta \varPhi_1+i_2 f_2 \nabla \Delta \varPhi_2+\cdots+i_k f_k \nabla \Delta \varPhi_k}{i_1 f_1+i_2 f_2+\cdots+i_k f_k} $ | (4) |
双差多频整周模糊度和组合波长可分别表示为:
| $ \begin{gathered} \nabla \Delta N_{\left(i_1, i_2, \cdots, i_k\right)}=i_1 \nabla \Delta N_1+ \\ i_2 \nabla \Delta N_2+\cdots+i_k \nabla \Delta N_k \end{gathered} $ | (5) |
| $ \begin{gathered} \lambda_{\left(i_1, i_2, \cdots, i_k\right)}= \\ \frac{c}{i_1 f_1+i_2 f_2+\cdots+i_k f_k} \end{gathered} $ | (6) |
一阶和二阶电离层尺度因子可分别表示为:
| $\beta_{\left(i_1, i_2, \cdots, i_k\right)}=\frac{f_1^2\left(\frac{i_1}{f_1}+\frac{i_2}{f_2}+\cdots+\frac{i_k}{f_k}\right)}{i_1 f_1+i_2 f_2+\cdots+i_k f_k} $ | (7) |
| $ \theta_{\left(i_1, i_2, \cdots, i_k\right)}=\frac{f_1^3\left(\frac{i_1}{f_1}+\frac{i_2}{f_2}+\cdots+\frac{i_k}{f_k}\right)}{i_1 f_1+i_2 f_2+\cdots+i_k f_k} $ | (8) |
观测噪声放大因子可表示为:
| $\begin{gathered} \eta_{\left(i_1, i_2, \cdots, i_k\right)}= \\ \frac{\sqrt{\left(i_1 f_1\right)^2+\left(i_2 f_2\right)^2+\cdots+\left(i_k f_k\right)^2}}{i_1 f_1+i_2 f_2+\cdots+i_k f_k} \end{gathered} $ | (9) |
假设不同频率的观测值具有相互独立的相等观测噪声,即满足
| $ \sigma_{\varepsilon \nabla \Delta P\left(i_1, i_2, \cdots, i_k\right)}^2=\eta_{\left(i_1, i_2, \cdots, i_k\right)}^2 \sigma_{\varepsilon \nabla \Delta P}^2 $ | (10) |
| $ \sigma_{\varepsilon \nabla \Delta \varPhi\left(i_1, i_2, \cdots, i_k\right)}^2=\eta_{\left(i_1, i_2, \cdots, i_k\right)}^2 \sigma_{\varepsilon \nabla \Delta \varPhi}^2 $ | (11) |
式中,
不同频率的伪距或载波相位观测值可以组成不同波长、不同电离层延迟影响和不同观测噪声的组合观测值。其中,高质量的组合观测值需要满足波长较长、电离层延迟影响较弱、观测噪声较小的条件,但是在部分线性组合中会存在电离层延迟尺度因子或噪声放大因子绝对值达到最小,但波长仍然较小的情况,会造成模糊度解算效果及定位性能不佳,因此本文考虑了除电离层延迟和观测噪声之外的其他各项误差。假设观测值中各误差项精度已知,通过定义总噪声水平(total noise level, TNL)来确定最优组合系数,以TNL最小原则作为组合系数的优选条件[8],伪距和载波相位的总噪声水平可分别表示为:
| $ \sigma_{T_P}=\sqrt{\sigma_{\nabla \Delta T}^2+\beta_{\left(i_1, i_2, \cdots, i_k\right)}^2 \sigma_{\nabla \Delta I_1}^2+\theta_{\left(i_1, i_2, \cdots, i_k\right)}^2 \sigma_{\nabla \Delta I_2}^2+\sigma_{\nabla \Delta \hat{o r r b}^2}^2+\sigma_{\varepsilon \Delta \Delta P\left(i_1, i_2, \cdots, i_k\right)}^2} $ | (12) |
| $\sigma_{T_{\varphi}}=\frac{1}{\lambda_{\left(i_1, i_2, \cdots, i_k\right)}} \sqrt{\sigma_{\nabla \Delta T}^2+\beta_{\left(i_1, i_2, \cdots, i_k\right)}^2 \sigma_{\nabla \Delta I_1}^2+\theta_{\left(i_1, i_2, \cdots, i_k\right)}^2 \sigma_{\nabla \Delta I_2}^2+\sigma_{\nabla \Delta \delta_{\text {orb }}}^2+\sigma_{\varepsilon \nabla \Delta \varPhi\left(i_1, i_2, \cdots, i_k\right)}^2} $ | (13) |
式中,
为确定最优组合系数,依据章浙涛等[14]的研究结果确定基线长度大于500 km时双差伪距和相位观测值各误差项的大致精度,具体见表 1。
|
|
表 1 长基线观测值各项误差精度 Tab. 1 Theerror precision of long-baseline observations |
在利用四频宽巷组合观测值进行定位时,首先基于几何无关模型,利用双差伪距组合观测值和双差相位组合观测值对双差超宽巷模糊度进行固定[9]:
| $ \nabla \Delta N_{\varPhi_1}=\left[\frac{\nabla \Delta P-\nabla \Delta \varPhi_1}{\lambda_{\varPhi_1}}\right]_{\mathrm{round}} $ | (14) |
式中,
模糊度浮点解精度可表示为:
| $ \sigma_{\nabla \Delta {N}_{\varPhi_1}}=\frac{1}{\lambda_{\varPhi_1}} \sqrt{\eta_P^2 \sigma_{\varepsilon \nabla \Delta P}^2+\eta_{\varPhi_1}^2 \sigma_{\varepsilon \nabla \Delta \varPhi}^2} $ | (15) |
式中,λΦ1为第1组双差超宽巷相位组合观测值对应的组合波长;ηP和ηΦ1分别为双差伪距组合观测值和第1组双差超宽巷相位组合观测值对应的观测噪声放大因子。
模糊度受到的电离层延迟偏差影响表示为:
| $ \delta_{\nabla \Delta N_{\varPhi_1}}=\frac{\beta_P+\beta_{\varPhi_1}}{\lambda_{\varPhi_1}} \nabla \Delta \iota $ | (16) |
式中,
以σTP和σTφ最小数值作为伪距和载波相位组合系数的优选条件。BDS-3和Galileo均可提供5个频点信号,本文BDS-3选用B1C、B1I、B2a、B3I四个频点,Galileo选用E1、E5a、E6、E5b四个频点[10],其他不同频点组合同样可应用于本文,限于篇幅,本文将不再作具体介绍。伪距组合系数的搜索范围设置在[-5, 5]之间,优选后的BDS-3和Galileo四频伪距组合系数分别为(5, 5, 2, 3)和(4, 2, 3, 2),其伪距总噪声水平分别为0.855 5 m和0.920 5 m,而对应BDS-3和Galileo的4组原始伪距总噪声水平均在1 m以上,明显高于优选的四频伪距组合的总噪声水平,因此对伪距组合进行优选具有必要性。相位组合系数的搜索范围设置在[-10, 10]之间,其中BDS-3和Galileo优选后的超宽巷组合系数分别为(1, -1, 0, 0)和(0, 2, 1 -3),其相位总噪声水平可分别达到0.078 1周和0.106 8周,在搜索范围内均各自达到最小值,模糊度浮点解精度分别为0.045 3周和0.077 4周,均可以达到100%的模糊度固定成功率,理论上可以实现模糊度的单历元固定。但其观测噪声放大因子分别达到154.858 0和440.273 8,直接使用该组合进行定位并不合适。为此需要选择另外具有较小观测值噪声的宽巷组合,将第1个模糊度改正后的超宽巷组合观测值作为精度更高的观测值,进而采用无几何模型对第2个宽巷模糊度进行单历元固定:
| $ \nabla \Delta N_{\varPhi_2}=\left[\frac{\left(\nabla \Delta \varPhi_1+\lambda_{\varPhi_1} \nabla \Delta N_{\varPhi_1}\right)-\nabla \Delta \varPhi_{\varPhi_2}}{\lambda_{\varPhi_2}}\right]_{\mathrm{round}} $ | (17) |
假设第1组超宽巷组合系数为(i1, j1, k1, l1),第2组宽巷组合系数为(i2, j2, k2, l2),则模糊度噪声和电离层延迟偏差影响可分别表示为:
| $ \sigma_{\nabla \Delta N_{\varPhi_2}}=\frac{1}{\lambda_{\varPhi_2}} \sigma_{\varepsilon \nabla \Delta \varPhi} \sqrt{\left(\frac{i_1 f_1}{f_{\varPhi_1}}+\frac{i_2 f_1}{f_{\varPhi_2}}\right)^2+\left(\frac{j_1 f_2}{f_{\varPhi_1}}+\frac{j_2 f_2}{f_{\varPhi_2}}\right)^2+\left(\frac{k_1 f_3}{f_{\varPhi_1}}+\frac{k_2 f_3}{f_{\varPhi_2}}\right)^2+\left(\frac{l_1 f_4}{f_{\varPhi_1}}+\frac{l_2 f_4}{f_{\varPhi_2}}\right)^2} $ | (18) |
| $ \delta_{N_{\varPhi_2}}=\frac{\beta_{\varPhi_1}+\beta_{\varPhi_2}}{\lambda_{\varPhi_2}} \nabla \Delta \iota $ | (19) |
优选后的BDS-3和Galileo第2组宽巷组合系数分别为(-1, 2, 2, -3)和(0, -1, 0, 1),此时模糊度解算受电离层延迟的影响系数为-0.470 3和-0.257 7,敏感程度较小。如当电离层影响达到0.2 m时,模糊度受到的偏差也仅为0.09周和0.05周,模糊度噪声分别为0.202 9周和0.199 1周,模糊度固定成功率分别达到98.32%和100%。在载波相位观测值精度较好的情况下,使用第2个宽巷组合观测值基本可以实现单历元模糊度固定。
当第2组宽巷模糊度解算完成之后,即可利用模糊度改正后的第2组宽巷观测值进行定位解算,定位解算方程可表示为:
| $ \begin{gathered} \nabla \Delta \widetilde{\varPhi}_2=\nabla \Delta \varPhi_2+\lambda_{\varPhi_2} \nabla \Delta N_{\varPhi_2}= \\ {\left[\begin{array}{llll} -\nabla \Delta l & -\nabla \Delta m & -\nabla \Delta n & -\beta_{\varPhi_2} \end{array}\right]\left[\begin{array}{c} \delta X \\ \delta Y \\ \delta Z \\ \nabla \Delta \iota \end{array}\right]} \end{gathered} $ | (20) |
式中,
利用式(20)即可以实现单一BDS-3系统或单一Galileo系统的定位解算,类似地可以得到基于宽巷组合的BDS-3/Galileo双系统定位解算模型:
| $\begin{aligned} & {\left[\begin{array}{c} \nabla \Delta \widetilde{\varPhi}_2^{\mathrm{C}} \\ \nabla \Delta \widetilde{\varPhi}_2^{\mathrm{E}} \end{array}\right]=\left[\begin{array}{l} \nabla \Delta \varPhi_2^{\mathrm{C}}+\lambda_{\varPhi_2}^{\mathrm{C}} \nabla \Delta N_{\varPhi_2}^{\mathrm{C}} \\ \nabla \Delta \varPhi_2^{\mathrm{E}}+\lambda_{\varPhi_2}^{\mathrm{E}} \nabla \Delta N_{\varPhi_2}^{\mathrm{E}} \end{array}\right]=} \\ & {\left[\begin{array}{cccc} -\nabla \Delta l & -\nabla \Delta m & -\nabla \Delta n & -\beta_{\varPhi_2}^{\mathrm{C}} \\ -\nabla \Delta l & -\nabla \Delta m & -\nabla \Delta n & -\beta_{\varPhi_2}^{\mathrm{E}} \end{array}\right]\left[\begin{array}{c} \delta X \\ \delta Y \\ \delta Z \\ \nabla \Delta c^{\mathrm{C}} \\ \nabla \Delta \iota^{\mathrm{E}} \end{array}\right]} \\ & \end{aligned} $ | (21) |
式中,C和E分别对应BDS-3和Galileo所表示的变量;
为进一步讨论加入GPS系统的定位性能,选择GPS的L1和L2频率,伪距组合为(1, 0),宽巷组合为(1, -1),利用式(14)可实现GPS超宽巷模糊度固定,进而得到基于宽巷组合的BDS-3/Galileo/GPS三系统定位解算模型:
| $\left[\begin{array}{c} \nabla \Delta \widetilde{\varPhi}_2^{\mathrm{C}} \\ \nabla \Delta \widetilde{\varPhi}_2^{\mathrm{E}} \\ \nabla \Delta \widetilde{\varPhi}_{(1, -1)}^{\mathrm{G}} \end{array}\right]=\left[\begin{array}{c} \nabla \Delta \varPhi_2^{\mathrm{C}}+\lambda_{\varPhi_2}^{\mathrm{C}} \nabla \Delta N_{\varPhi_2}^{\mathrm{C}} \\ \nabla \Delta \varPhi_2^{\mathrm{E}}+\lambda_{\varPhi_2}^{\mathrm{E}} \nabla \Delta N_{\varPhi_2}^{\mathrm{E}} \\ \nabla \Delta \varPhi_{(1, -1)}^{\mathrm{G}}+\lambda_{\varPhi_{(1, -1)}^{\mathrm{G}}} \nabla \Delta N_{\varPhi_{(1, -1)}^{\mathrm{G}}}^{\mathrm{G}} \end{array}\right]=\\ \begin{aligned} & {\left[\begin{array}{cccc} -\nabla \Delta l-\nabla \Delta m & -\nabla \Delta n & -\beta_{\varPhi_2}^{\mathrm{C}} \\ -\nabla \Delta l-\nabla \Delta m & -\nabla \Delta n & -\beta_{\varPhi_2}^{\mathrm{E}} \\ -\nabla \Delta l-\nabla \Delta m & -\nabla \Delta n & -\beta_{\varPhi_{(1, -1)}}^{\mathrm{G}} \end{array}\right]\left[\begin{array}{c} \delta X \\ \delta Y \\ \delta Z \\ \nabla \Delta \iota^{\mathrm{C}} \\ \nabla \Delta \iota^{\mathrm{E}} \\ \nabla \Delta \iota^{\mathrm{G}} \end{array}\right]} \\ & \end{aligned} $ | (22) |
式中,G对应GPS所表示的变量;
本文选择2021年doy200由IGS提供的SUTM(32.38°S, 20.81°E)、WIND(22.57°S, 17.09°E)、MET3(60.22°N, 24.39°E)、SOD3(67.42°N, 26.38°E)四个站点的数据,采样间隔为30 s,观测时间为24 h。其中,由SUTM和WIND组成的基线用“基线1”表示,基线长度为620.45 km;由MET3和SOD3组成的基线用“基线2”表示,基线长度为726.59 km。
首先对2个测站卫星的可用性进行分析,基线1和基线2在研究时段观测到的卫星数与PDOP值分别如图 1和2所示。可以看出,2条基线BDS-3和Galileo的可视卫星数均超过4颗,其中基线1的可视卫星数均保持在6颗左右,基线2保持在8颗左右,单系统均可以满足定位服务。BDS-3和Galileo单系统的PDOP值均小于6,能满足独立三维导航定位的要求,而对于BDS-3/Galileo双系统,PDOP值保持在1左右,BDS-3/Galileo/GPS三系统PDOP值均小于1。随着卫星系统的增加,卫星空间几何分布得到较大改善。
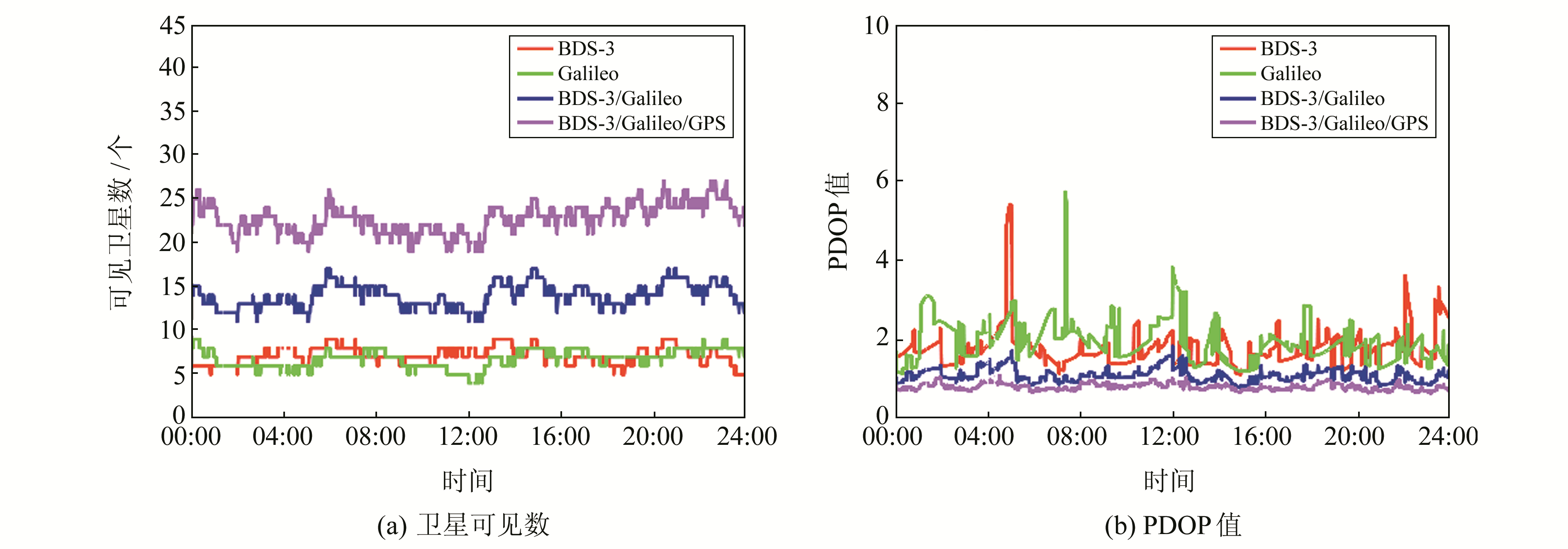
|
图 1 基线1卫星可见数与PDOP值 Fig. 1 The number of visible satellites and PDOP of baseline 1 |
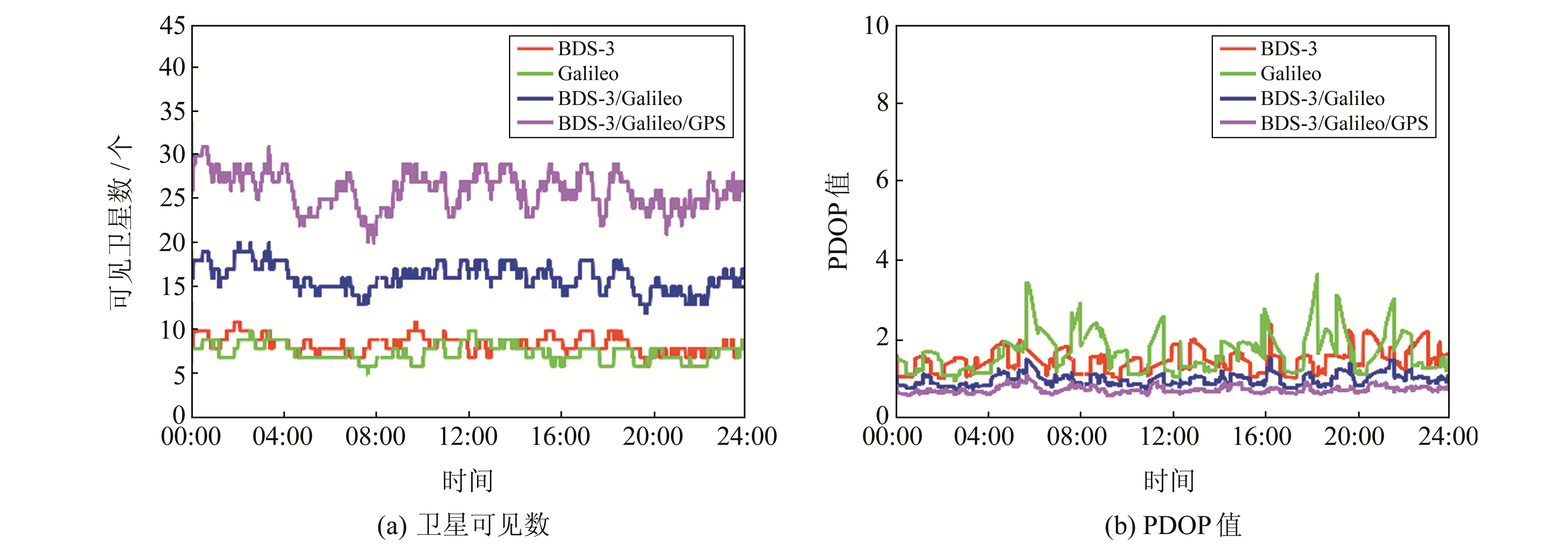
|
图 2 基线2卫星可见数与PDOP值 Fig. 2 The number of visible satellites and PDOP of baseline 2 |
以模糊度固定成功率指标对BDS-3和Galileo第2组四频宽巷模糊度的固定效果进行分析。表 2为2条基线部分卫星对的第2组宽巷模糊度固定成功率。从表中可以看出,BDS-3卫星对的宽巷模糊度固定成功率可以保持在90%以上,甚至可以达到100%,而Galileo卫星对的宽巷模糊度固定成功率仅能保持在60%~70%之间。其原因可能是Galileo相位观测值的精度较差,观测值中部分误差无法被完全消除。需要说明的是,对于本文选取的2条超过500 km的长基线,在相对定位过程中会受到较短基线更大的误差影响,从而导致相位观测值精度较差,造成BDS-3和Galileo第2组宽巷模糊度固定成功率无法达到理论水平。但考虑到第2组宽巷观测值较第1组超宽巷观测值具有更小的观测噪声放大因子,且受到的观测噪声和电离层影响更小,为此选择第2组宽巷组合观测值进行定位解算。
|
|
表 2 BDS-3/Galileo基线1和基线2宽巷模糊度固定成功率 Tab. 2 The WL ambiguity resolution successful rate of baseline 1 and baseline 2 for BDS-3 and Galileo |
对2条基线下单系统、双系统和三系统组合定位对应的北东天方向定位结果偏差进行分析,图 3和4分别为2条基线的定位结果偏差。可以看出,当采用BDS-3单系统或Galileo单系统进行定位时,2个系统整体定位精度相当,两条基线N方向和E方向的定位误差保持在-2~2 m之间,U方向定位误差保持在-6~6 m之间,而某些时刻单系统定位偏差存在较大波动,尤其是在U方向。当采用BDS-3/Galileo双系统进行定位时,水平方向和垂直方向的定位精度均得到明显改善,2条基线N方向和E方向的定位误差保持在-1~1 m之间,U方向定位误差保持在-2~2 m之间,由此推测双系统定位可有效地消除单系统定位U方向的较大定位偏差。当采用加入GPS系统的三系统进行定位时,改善效果并不显著,但整体来说定位结果更趋稳定。
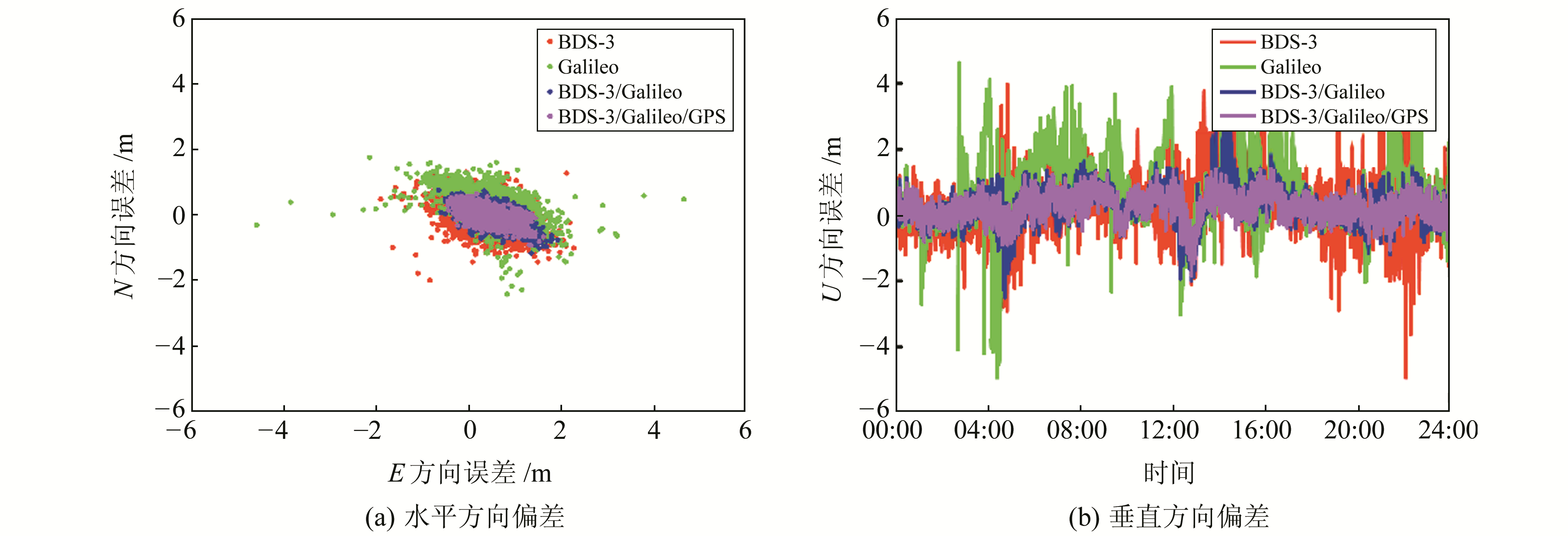
|
图 3 基线1定位结果偏差 Fig. 3 The positioning errors of baseline 1 |
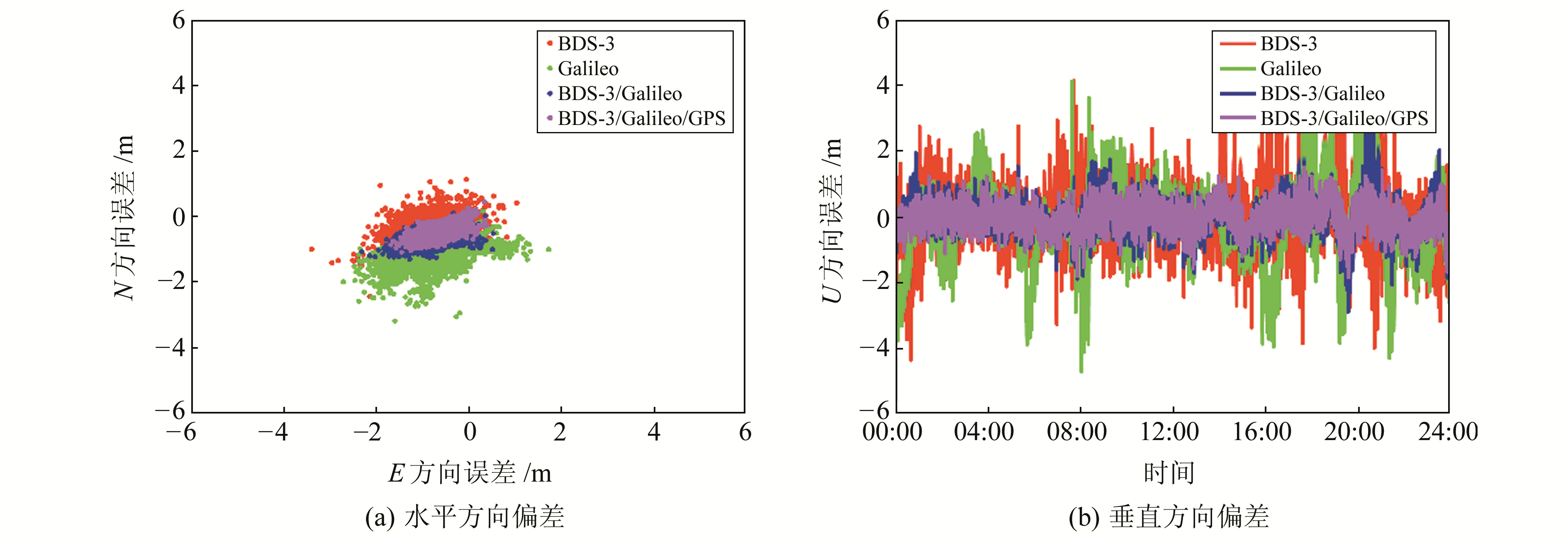
|
图 4 基线2定位结果偏差 Fig. 4 The positioning errors of baseline 2 |
为更直观地表示定位精度,对2条基线定位结果的均方根误差RMSE进行统计,表 3(单位m)和4(单位m)分别为基线1和基线2不同系统定位结果的RMSE统计值。由表可知,Galileo单系统三维方向上存在超过1 m的定位误差,定位精度较差,BDS-3较Galileo在N、E、U三方向上的定位精度更高,2条基线下BDS-3较Galileo在水平方向分别提高了22.37%和24.70%,垂直方向分别提高了31.82%和20.87%。当采用BDS-3/Galileo双系统组合定位时,N、E、U三方向较单系统定位时的定位精度均有明显提高,水平方向2条基线定位精度分别优于0.5 m和0.8 m,垂直方向分别优于0.6 m和0.7 m。在水平方向上,双系统较BDS-3单系统的定位精度提升并不显著,但在垂直方向上,双系统较BDS-3单系统的定位精度提升较明显,可分别提升34.04%和39.63%。当引入GPS系统构成三系统定位时,水平方向2条基线定位精度分别优于0.4 m和0.7 m,较双系统定位精度分别提高了19.82%和9.25%;垂直方向分别优于0.6 m和0.7 m,较双系统定位精度分别提高了21.13%和21.41%。由此可见,加入GPS系统的三系统定位精度较双系统更高。
|
|
表 3 基线1不同系统定位结果RMSE统计 Tab. 3 The RMSE of different system positioningresults of baseline 1 |
|
|
表 4 基线2不同系统定位结果RMSE统计 Tab. 4 The RMSE of different system positioningresults of baseline 2 |
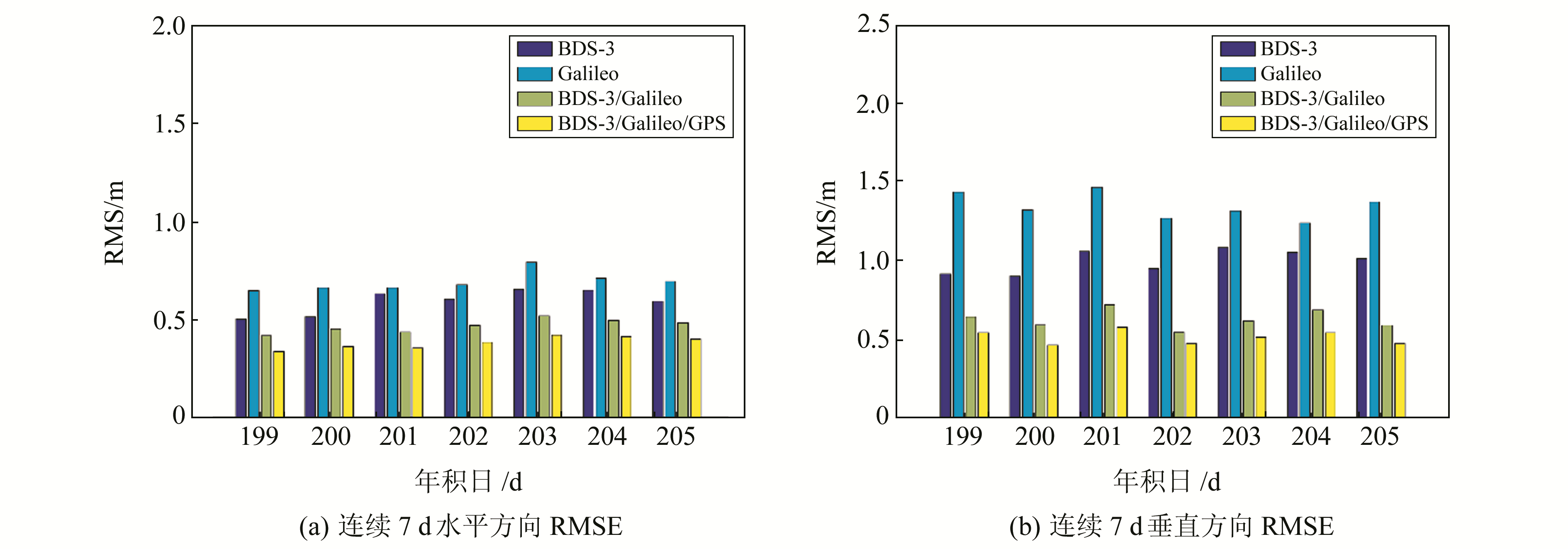
对2021年doy199~205的RMSE值进行统计,2条基线下单天定位结果的RMSE如图 5和6所示。可以看出,单系统模式下,BDS-3较Galileo的定位精度更高,水平方向精度平均在0.8 m左右,垂直方向定位精度平均在1.0 m左右;双系统水平和垂直方向的定位精度均保持在0.7 m左右,水平方向较BDS-3单系统的提升幅度仅为10%左右,但垂直方向提升幅度较显著,可以达到25%以上;三系统水平和垂直方向上的定位精度均保持在0.5 m左右,较双系统提升幅度均较小,在10%左右。本文多系统组合可实现亚m级长基线定位,在水平方向上可达到与Li等[6]和Feng等[7]的三频组合观测值及Liu等[10]的BDS-3/Galileo多频组合观测值相同数量级的定位精度,在垂直方向上的提升幅度较明显,可从m级提高到亚m级水平。综合考虑水平和垂直方向定位结果,本文构建的多频多系统定位模型在长基线场景下具有一定优势。此外,本文选用的2条长基线长度均超过500 km,双系统和三系统的相对定位精度均达到1×10-9 m,可满足高精度相对定位解算的需求。
|
图 5 基线1单天定位结果均方根误差 Fig. 5 The RMSE of single day positioning results of baseline 1 |
|
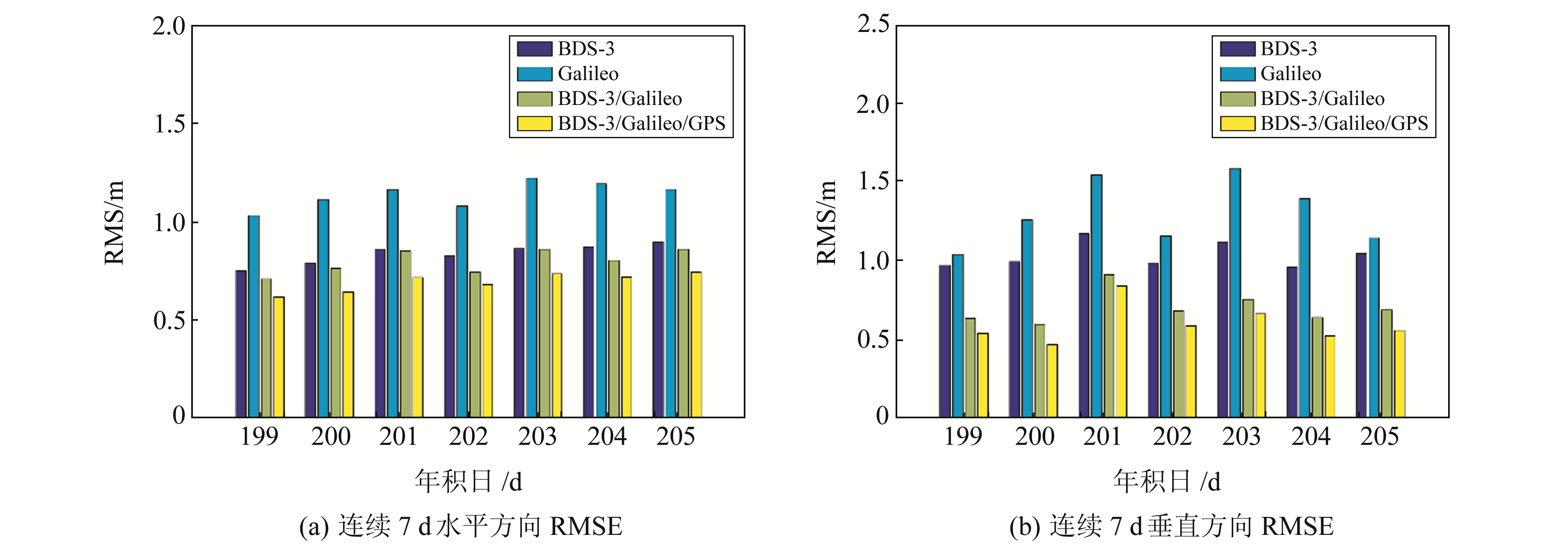
图 6 基线2单天定位结果均方根误差 Fig. 6 The RMSE of single day positioning results of baseline 2 |
采用总噪声水平最小原则对BDS-3和Galileo四频宽巷组合系数进行优选,基于优选的宽巷组合构建单系统、双系统及三系统定位方程,利用2条长基线数据对BDS-3单系统、Galileo单系统、BDS-3/Galileo双系统及BDS-3/Galileo/GPS三系统4种定位方式进行测试,旨在对长基线场景下多频组合定位性能进行分析。结果表明,BDS-3单系统定位较Galileo单系统的定位精度有明显改善,BDS-3/Galileo双系统定位在水平和垂直方向的定位精度均可达dm级,水平和垂直方向的定位精度可保持在0.7 m以内,较BDS-3单系统定位精度提升幅度保持在10%和25%以上,定位结果也更加稳定。BDS-3/Galileo/GPS三系统组合定位精度较双系统组合定位均有所提升,水平和垂直方向的定位精度可达0.6 m和0.5 m,较双系统提升幅度在10%左右。总体来看,对于本文选用的2条长度超过500 km的基线,双系统和三系统的相对定位精度均可达到1×10-9 m,可满足长基线精密定位的需求。因此,采用多频多系统组合定位可有效提高长基线相对定位的精度和稳定性,拓宽未来高精度相对定位服务在长基线场景下的应用。
| [1] |
Odolinski R, Teunissen P J G. Low-Cost, High-Precision, Single-Frequency GPS-BDS RTK Positioning[J]. GPS Solutions, 2017, 21(3): 1 315-1 330 DOI:10.1007/s10291-017-0613-x
(  0) 0) |
| [2] |
He H B, Li J L, Yang Y X, et al. Performance Assessment of Single- and Dual-Frequency Beidou/GPS Single-Epoch Kinematic Positioning[J]. GPS Solutions, 2014, 18(3): 393-403 DOI:10.1007/s10291-013-0339-3
(  0) 0) |
| [3] |
王楚扬, 秘金钟, 李勇熹, 等. BDS-3/GPS/Galileo组合动态差分定位算法研究[J]. 测绘科学, 2022, 47(2): 16-22 (Wang Chuyang, Bei Jinzhong, Li Yongxi, et al. Research on BDS/GPS/Galileo Combination RTK Location Algorithm[J]. Science of Surveying and Mapping, 2022, 47(2): 16-22)
(  0) 0) |
| [4] |
刘金海, 涂锐, 张鹏飞, 等. GPS/GLONASS/BDS组合的RTK模型与精度分析[J]. 测绘科学, 2019, 44(1): 144-150 (Liu Jinhai, Tu Rui, Zhang Pengfei, et al. The Model and Accuracy Analysis of Combined RTK by GPS, GLONASS and BDS[J]. Science of Surveying and Mapping, 2019, 44(1): 144-150)
(  0) 0) |
| [5] |
陈文涛, 程鹏飞, 徐彦田, 等. 单差模糊度的BDS/GLONASS多频RTK算法[J]. 测绘科学, 2020, 45(4): 7-12 (Chen Wentao, Cheng Pengfei, Xu Yantian, et al. BDS/GLONASS Multi-Frequency RTK Algorithm Based on Single Difference Ambiguity[J]. Science of Surveying and Mapping, 2020, 45(4): 7-12)
(  0) 0) |
| [6] |
Li B F, Feng Y M, Gao W G, et al. Real-Time Kinematic Positioning over Long Baselines Using Triple-Frequency Beidou Signals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(4): 3 254-3 269 DOI:10.1109/TAES.2015.140643
(  0) 0) |
| [7] |
Feng Y M, Li B F. Wide Area Real Time Kinematic Decimetre Positioning with Multiple Carrier GNSS Signals[J]. Science China Earth Sciences, 2010, 53(5): 731-740 DOI:10.1007/s11430-010-0032-0
(  0) 0) |
| [8] |
张超, 闻道秋, 潘树国, 等. 基于北斗三频宽巷组合的RTK单历元定位方法[J]. 测绘工程, 2015, 24(6): 28-32 (Zhang Chao, Wen Daoqiu, Pan Shuguo, et al. Single Epoch Algorithm of Short Baseline RTK Based on Triple-Frequency Wide-Lane Combination of BDS[J]. Engineering of Surveying and Mapping, 2015, 24(6): 28-32)
(  0) 0) |
| [9] |
高旺, 高成发, 潘树国, 等. 北斗三频宽巷组合网络RTK单历元定位方法[J]. 测绘学报, 2015, 44(6): 641-648 (Gao Wang, Gao Chengfa, Pan Shuguo, et al. Single-Epoch Positioning Method in Network RTK with BDS Triple-Frequency Widelane Combinations[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(6): 641-648)
(  0) 0) |
| [10] |
Liu L W, Pan S G, Gao W, et al. Assessment of Quad-Frequency Long-Baseline Positioning with Beidou-3 and Galileo Observations[J]. Remote Sensing, 2021, 13(8)
(  0) 0) |
| [11] |
李振, 李博峰. BDS超宽巷实时定位分析[J]. 导航定位学报, 2017, 5(3): 44-51 (Li Zhen, Li Bofeng. Analysis on Real-Time Kinematic Positioning of BDS with EWL[J]. Journal of Navigation and Positioning, 2017, 5(3): 44-51)
(  0) 0) |
| [12] |
Li B F, Li Z, Zhang Z T, et al. ERTK: Extra-Wide-Lane RTK of Triple-Frequency GNSS Signals[J]. Journal of Geodesy, 2017, 91(9): 1 031-1 047
(  0) 0) |
| [13] |
Zhang Z T. Code and Phase Multipath Mitigation by Using the Observation-Domain Parameterization and Its Application in Five-Frequency GNSS Ambiguity Resolution[J]. GPS Solutions, 2021, 25(4)
(  0) 0) |
| [14] |
章浙涛, 李博峰, 何秀凤. 北斗三号多频相位模糊度无几何单历元固定方法[J]. 测绘学报, 2020, 49(9): 1 139-1 148 (Zhang Zhetao, Li Bofeng, He Xiufeng. Geometry-Free Single-Epoch Resolution of BDS-3 Multi-Frequency Carrier Ambi-Guities[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1 139-1 148)
(  0) 0) |
2. Shengli Branch of SINOPEC Geophysical Co Ltd, 173 Zhenqian Road, Dongying 257100, China;
3. Qingdao Beidou Land-Sea Technology Co Ltd, 480 South-Jiangshan Road, Qingdao 266555, China
 2023, Vol. 43
2023, Vol. 43

