2. 西安测绘研究所,西安市雁塔中路1号,710054;
3. 长安大学地质工程与测绘学院,西安市雁塔路126号,710054
硬件延迟偏差是影响定位精度的重要因素之一,常用的硬件偏差产品主要有随广播星历实时播发的时间群延迟(timing group delay,TGD)参数和IGS分析中心提供的高精度事后差分码偏差(differential code bias,DCB)产品[1]。目前BDS-3广播星历以B3I为基准,广播星历实时播发的TGD1和TGD2分别表示B1I与B2I信号的设备时延与基准时延的差值,其不确定度小于1 ns;TGDB1Cp和TGDB2ap分别表示B1C导频分量与B2a导频分量的时延差[2-3]。此外ISCB1Cd和ISCB2ad分别用于补偿B1C和B2a频点数据分量和导频分量间的时间差[4-6]。
虽然相较于DCB,TGD参数的精度低且更新周期长[7],但TGD参数随广播星历实时播发,具有更强的实用性。已有学者针对B1、B2、B3频点的TGD改正进行了相关研究,但对于BDS-3新频点的研究相对较少。由于新频点的增加为BDS-3不同频率组合提供了更多可能[8],同时硬件延迟偏差可以对单点定位产生dm~m级的影响[9],因此探究TGD改正对BDS-3定位精度的影响十分必要。基于此,本文总结单频和不同频点组合双频TGD改正公式,分析TGD参数和DCB产品符合度及DCB产品的稳定性,并采用MGEX跟踪站数据进行SPP实验,讨论TGD改正对BDS-3 SPP定位精度的影响。
1 观测方程及TGD改正公式 1.1 伪距观测方程原始伪距观测方程可表示为:
| $\begin{gathered} P_{\mathrm{r}}^{\mathrm{s}}=\rho_{\mathrm{r}}^{\mathrm{s}}+c \cdot \mathrm{d} t_{\mathrm{r}}-c \cdot \mathrm{d} t^{\mathrm{s}}+ \\ T_{\mathrm{r}}^{\mathrm{s}}+I_{\mathrm{r}}^{\mathrm{s}}+b_{\mathrm{r}}-b^{\mathrm{s}}+\varepsilon_{\mathrm{r}}^{\mathrm{s}} \end{gathered} $ | (1) |
式中,Prs为码观测值,s和r分别为卫星和接收机,ρrs为卫星与接收机之间的几何距离,c为真空中的光速,dts和dtr分别为卫星和接收机钟差,Trs为对流层延迟,Irs为电离层延迟,bs和br分别为卫星和接收机端的硬件延迟,εrs为伪距的多路径误差和观测噪声。
当采用不同频率观测值进行无电离层组合时,伪距观测方程可表示为:
| $\begin{gathered} P_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}}=\alpha \cdot P_{\mathrm{r}, i}^{\mathrm{s}}+\beta \cdot P_{\mathrm{r}, j}^{\mathrm{s}}=\rho_{\mathrm{r}}^{\mathrm{s}}+ \\ c \cdot \mathrm{d} t_{\mathrm{r}}-c \cdot \mathrm{d} t^{\mathrm{s}}+T_{\mathrm{r}}^{\mathrm{s}}+b_{\mathrm{r}, \mathrm{IF}}-b_{\mathrm{IF}}^{\mathrm{s}}+\varepsilon_{\mathrm{r}, \mathrm{IF}}^{\mathrm{s}} \end{gathered} $ | (2) |
式中,α=fi2/(fi2-fj2),β=-fj2/(fi2-fj2),i和j为2个不同的频点,fi和fj为其对应的频率,IF为两频点无电离层组合,其他符号含义同式(1)。
1.2 基于广播星历的TGD改正公式目前BDS-3广播星历以B3I为基准,当使用B3I频点进行SPP解算时无需顾及TGD改正,而接收机端硬件延迟偏差通常可吸收至接收机钟差中进行计算[10],故BDS-3单频SPP的TGD改正公式为:
| $ \left\{\begin{array}{l} b_{\mathrm{B} 1 \mathrm{I}}^{\mathrm{s}}=T_{\mathrm{GD} 1} \\ b_{\mathrm{B} 1 \mathrm{C}}^{\mathrm{s}}=T_{\mathrm{GDB} 1 \mathrm{Cp}} \\ b_{\mathrm{B} 2 \mathrm{a}}^{\mathrm{s}}=T_{\mathrm{GDB} 2 \mathrm{ap}} \\ b_{\mathrm{B} 31}^{\mathrm{s}}=0 \end{array}\right. $ | (3) |
其中,TGD参数老频点B1I取自IGS提供的广播星历,新频点B1C和B2a取自iGMAS提供的BDS-3新广播星历。
当使用不同频点进行无电离层组合时,因B1I/B1C和B2a/B3I组合的噪声系数过大(77.43和9.43,其余组合大多为2~4),故不考虑这2种频点组合。B1I/B3I、B1C/B3a、B1I/B2a和B1C/B3I组合的改正公式为:
| $ \left\{\begin{array}{l} b_{\mathrm{B} 11 / \mathrm{B} 3 \mathrm{I}}^{\mathrm{s}}=\frac{f_{\mathrm{B} 1 \mathrm{I}}^2}{f_{\mathrm{B} 1 \mathrm{I}}^2-f_{\mathrm{B} 3 \mathrm{I}}^2} T_{\mathrm{GD} 1} \\ b_{\mathrm{B} 1 \mathrm{C} / \mathrm{B} 2 \mathrm{a}}^{\mathrm{s}}=\frac{f_{\mathrm{B} 1 \mathrm{C}}^2 T_{\mathrm{GDB} 1 \mathrm{Cp}}-f_{\mathrm{B} 2 \mathrm{a}}^2 T_{\mathrm{GDB} 2 \mathrm{ap}}}{f_{\mathrm{B} 1 C}^2-f_{\mathrm{B} 2 \mathrm{a}}} \\ b_{\mathrm{B} 1 / \mathrm{B} 2 \mathrm{a}}^{\mathrm{s}}=\frac{f_{\mathrm{B} 1 \mathrm{I}}^2 T_{\mathrm{GD1}}-f_{\mathrm{B} 2 \mathrm{a}}^2 T_{\mathrm{GDB} 2 \mathrm{ap}}}{f_{\mathrm{B} 1 \mathrm{I}}^2-f_{\mathrm{B} 2 \mathrm{a}}^2} \\ b_{\mathrm{B} 1 \mathrm{C} / \mathrm{B} 3 \mathrm{I}}^{\mathrm{s}}=\frac{f_{\mathrm{B} 1 \mathrm{C}}^2}{f_{\mathrm{B} 1 \mathrm{C}}^2-f_{\mathrm{B} 3 \mathrm{I}}^2} T_{\mathrm{GDB} 1 \mathrm{Cp}} \end{array}\right. $ | (4) |
为分析TGD改正对BDS-3单、双频SPP定位精度的影响,本文选取全球范围内10个MGEX跟踪站2022-04-01~30(doy 91~120)连续30 d的BDS-3观测数据进行SPP解算,所有测站均可接收B1I、B1C、B2a和B3I频点数据,采样率为30 s。BDS-3 GEO卫星不播发新频点B1C、B2a信号,因此仅采用C19~C46参与解算,截止高度角为7°。测站真值坐标取自IGS提供的SNX文件,单频电离层延迟改正采用BDGIM模型修正,双频采用无电离层组合,对流层延迟改正利用Saastamoinen模型,TGD参数TGD1来源于IGS提供的广播星历,TGDB1Cp和TGDB2ap来源于iGMAS提供的广播星历。
为分析DCB产品的稳定性及TGD参数与DCB产品的符合度,本文统计10个测站30 d的平均可见卫星数和PDOP值,按照2个方案进行SPP实验:1)方案1,对B1I、B1C和B2a频点进行单频SPP解算,B1I/B3I、B1C/B2a、B1I/B2a和B1C/B3I组合进行双频SPP解算,均不考虑TGD改正;2)方案2,在方案1的解算中加入TGD改正,其余处理策略均相同。获得解算结果后与真值作差,并计算其均方根误差RMSE。为直观说明TGD改正前后对定位结果的影响,本文在作图时未将误差较大的历元剔除,而在统计RMSE时将大于20 m的历元视为粗差剔除[11]。
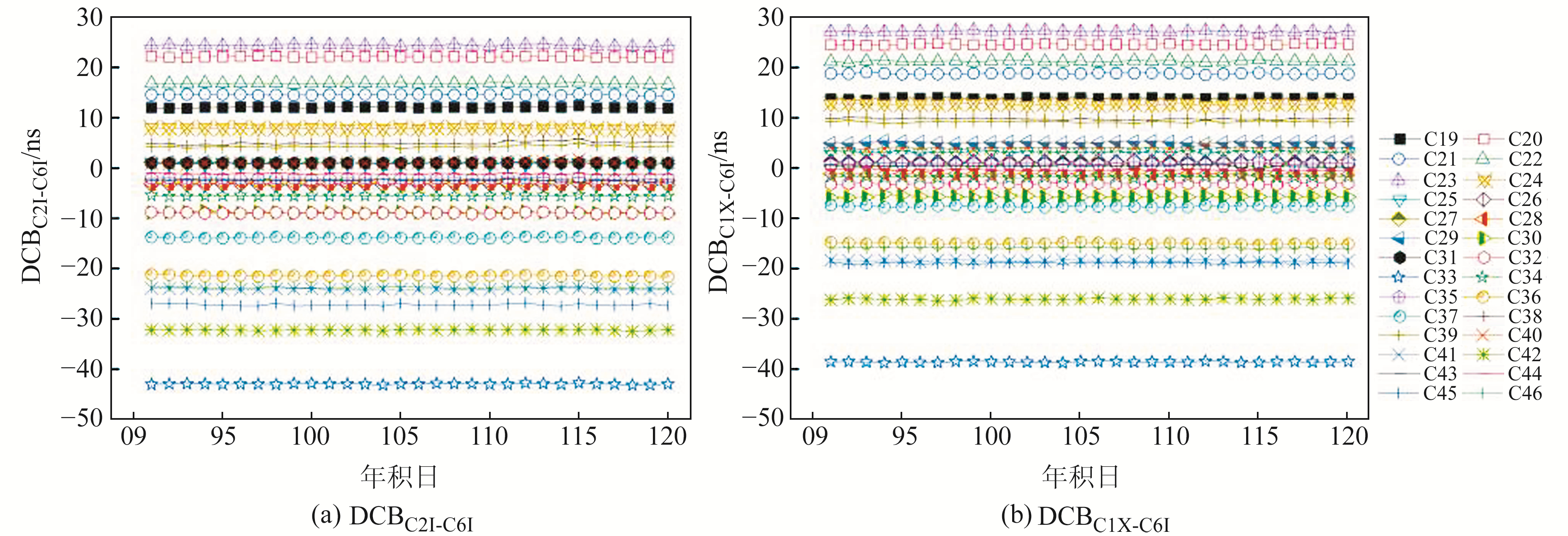
2.2 DCB稳定性及与TGD的符合度为探究BDS-3 DCB产品的稳定性和TGD参数与DCB产品的差异,图 1为中国科学院CAS提供的连续30 d DCB产品DCBC2I-C6I和DCBC1X-C6I日解值序列,图 2为2022-04-01各颗BDS-3卫星的TGD与DCB值及TGD与DCB的差异。TGD参数和DCB产品中均缺少C31卫星,因为其为2015-03-30发射的BDS-3试验卫星,信号体制与BDS-3不完全相同,且不属于BDS-3。
|
图 1 CAS DCB产品时间序列 Fig. 1 Time series of CAS DCB |

|
图 2 BDS-3卫星TGD与DCB Fig. 2 BDS-3 satellite TGD and DCB values |
由图 1可知,DCBC2I-C6I日解值的分布范围约为-45~25 ns,DCBC1X-C6I日解值的分布范围约为-40~30 ns,连续1个月的DCB产品日解值稳定,未出现明显跳变。DCBC2I-C6I中C38的稳定性最差,其标准差STD约为0.30 ns,其中C29卫星最优,STD约为0.08 ns;相较于DCBC2I-C6I,DCBC1X-C6I的稳定性稍优,其中C43卫星的稳定性最差,STD为0.20 ns,C46卫星最优,STD为0.09 ns,大部分卫星的月稳定性优于0.2 ns。由图 2可见,TGD参数与DCB产品差异不大,大部分卫星差异优于2 ns。
2.3 可见卫星数及PDOP值卫星的数量和空间几何构型会影响定位精度,表 1为各测站30 d的平均可见卫星数和PDOP值。
|
|
表 1 平均可见卫星数和PDOP Tab. 1 Average number of visible stars and PDOP |
由表 1可见,除GOP6站平均可见卫星数为6.4颗、PDOP为2.9外,其他测站可见卫星数均为8~11颗、PDOP约为2,说明目前BDS-3可见卫星数量稳定,且卫星空间几何构型良好。
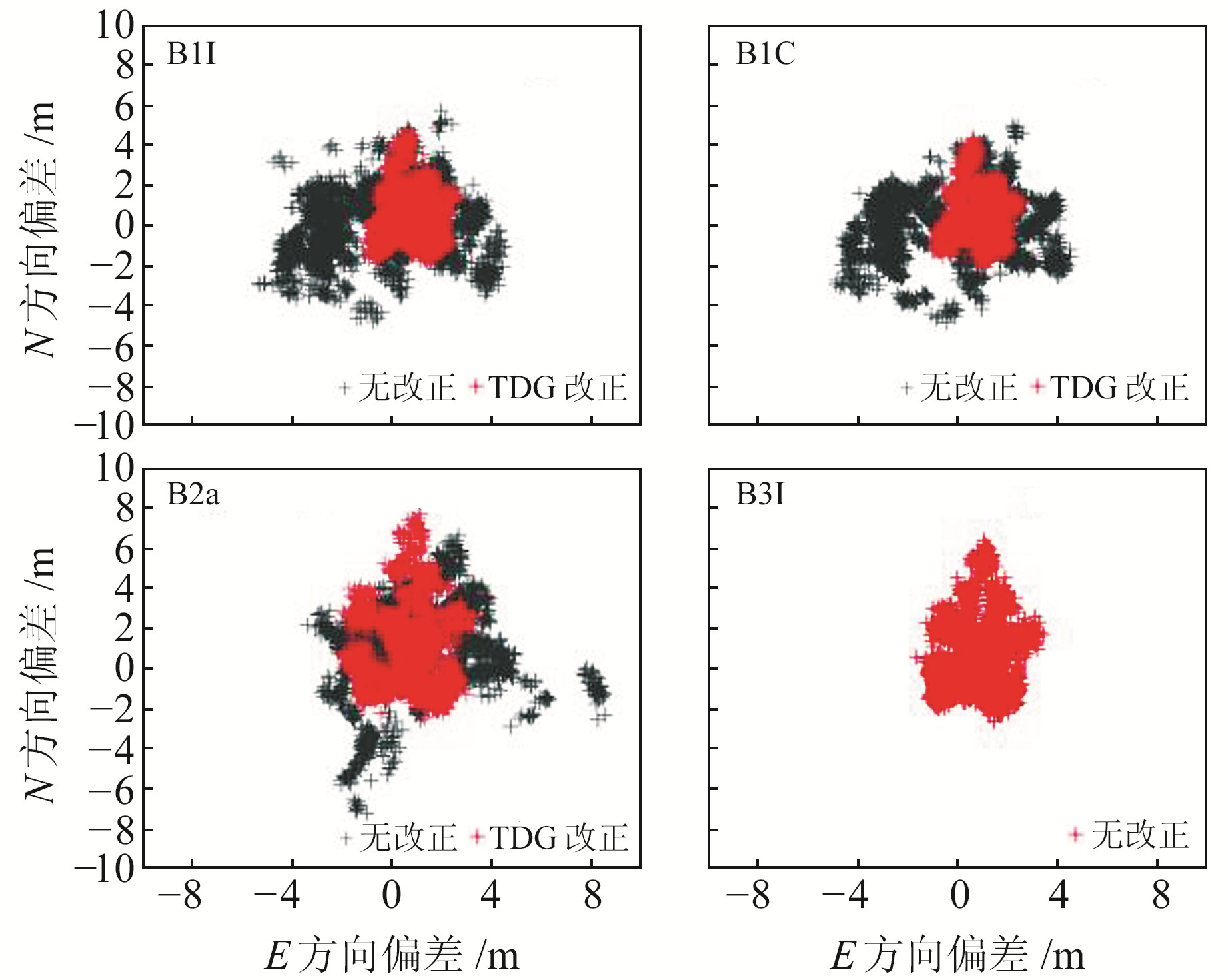
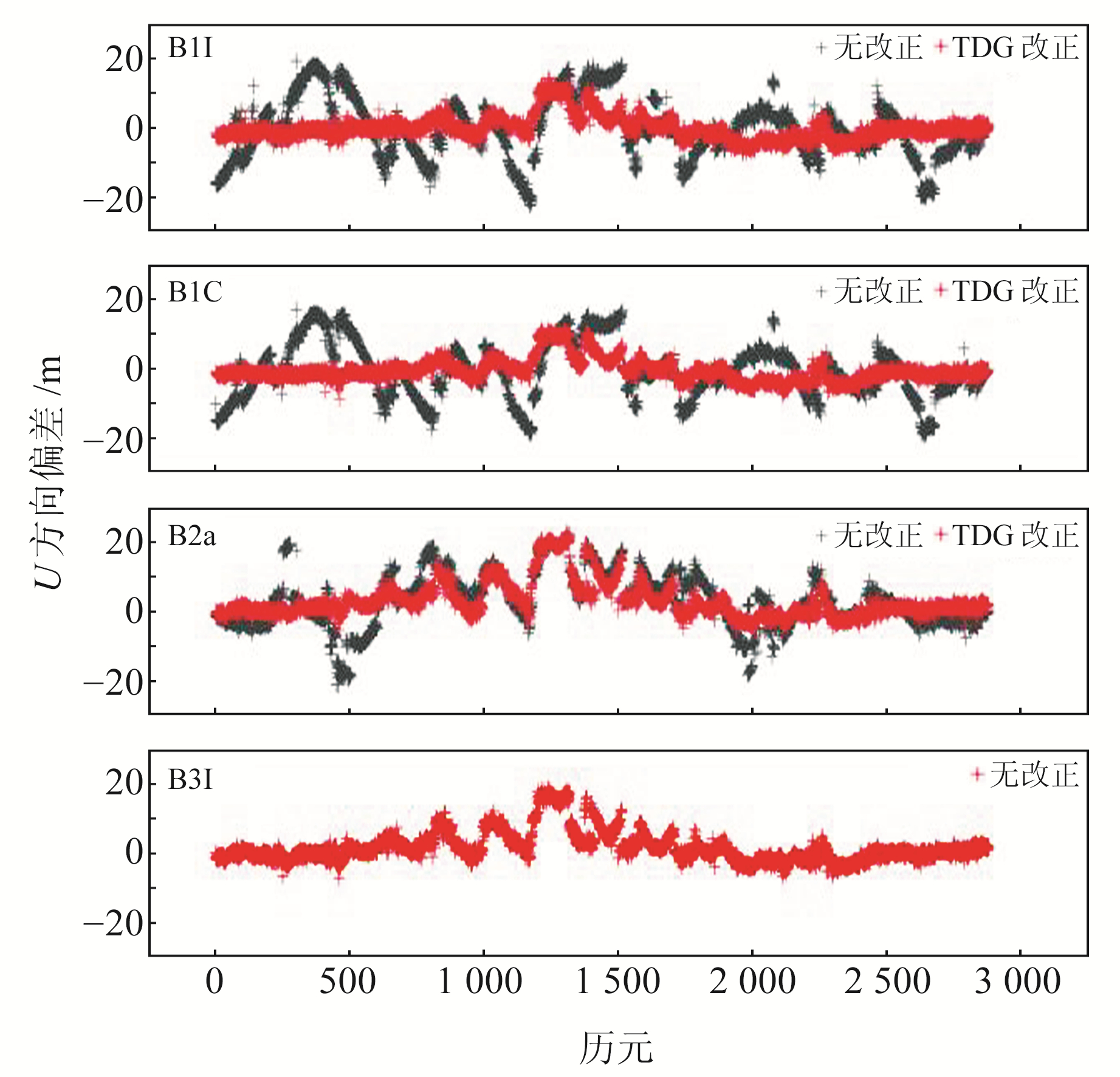
2.4 单频SPP精度分析图 3和4分别为具有代表性的NYA2站2022-04-01 B1I、B1C、B2a和B3I单频SPP水平和高程方向TGD改正前后的定位偏差,表 2为不同频点TGD改正前后的定位精度。由图 3和4可见,经TGD改正后,无论水平还是高程方向的精度均有大幅提升,水平方向距坐标原点中心更紧密,高程方向波动更小,且能直观地看出B2a频点水平和高程方向改正效果较其余频点稍差。B3I频点虽没有经过TGD改正,但其水平和高程方向的定位精度与其他频点改正后基本相同,证明B3I频点因钟差基准问题无需进行TGD改正。因篇幅有限,本文仅给出单日单站序列,其余测站与之类似。
|
图 3 NYA2站单频SPP水平方向定位偏差 Fig. 3 NYA2 station single-frequency SPP horizontalcomponent deviation |
|
图 4 NYA2站单频SPP高程方向定位偏差 Fig. 4 NYA2 station single-frequency SPP verticalcomponent positioning deviation |
|
|
表 2 单频SPP TGD改正前后定位精度 Tab. 2 Positioning accuracy before and after TGDcorrection of single-frequency SPP |
由表 2可见,B1I和B1C频点改正效果相当,均优于B2a,水平方向的定位精度由2~4 m改善至1 m左右,提升率为60%~70%;高程方向的提升率稍低,由约8 m精度提升至3 m,提升率约为50%。B2a频点的改善效果稍差,原因可能是其频率与B3I相近,受到的改正影响较小,但其在E、N方向的定位精度分别由2.54 m和2.70 m改正至1.33 m和1.73 m,提升率分别为43.0%和31.6%;U方向的改正效果稍差,由7.25 m提升至5.62 m,提升率约为17.7%。B3I频点未经TGD改正的精度在E、N、U方向分别为1.17 m、1.46 m和4.67 m,与其余频点改正后的精度基本相当。
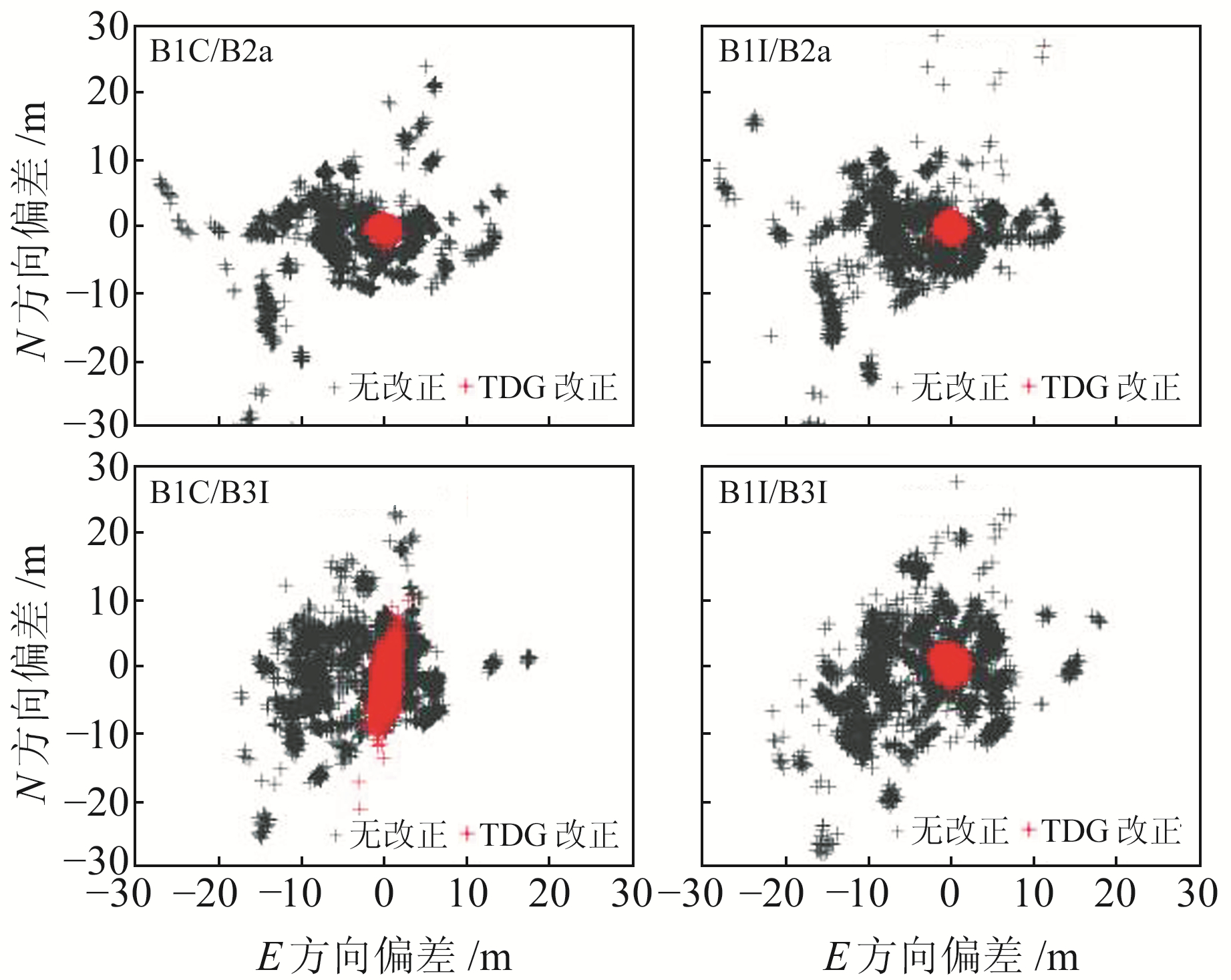
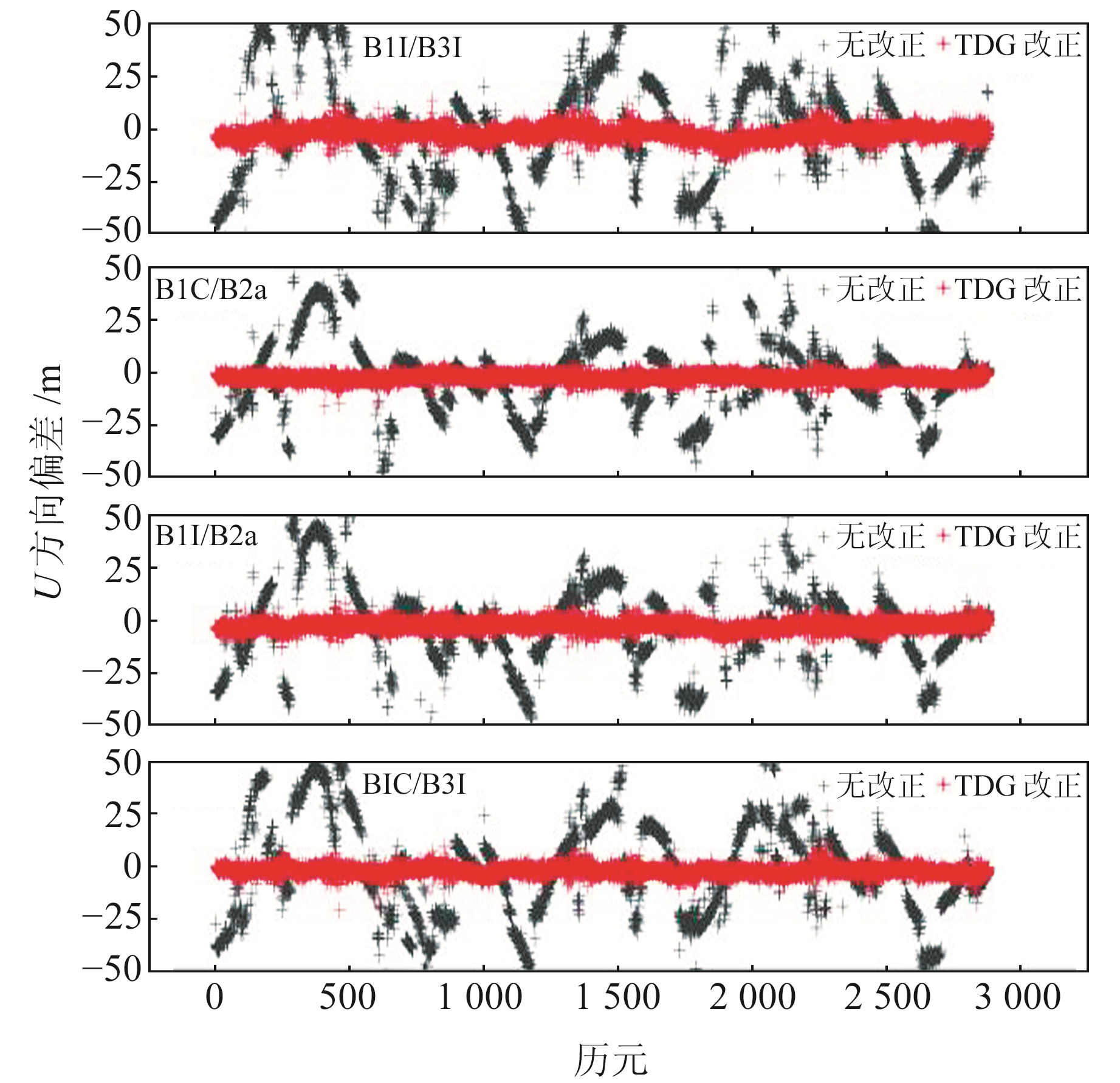
2.5 双频SPP精度分析按照方案1和方案2进行双频解算后,图 5和6分别为2022-04-01 NYA2站B1I/B3I、B1C/B2a、B1I/B2a和B1C/B3I双频SPP水平和高程方向TGD改正前后的定位偏差,表 3为双频SPP TGD改正前后的定位精度。
|
图 5 NYA2站双频SPP水平方向定位偏差 Fig. 5 NYA2 station dual-frequency SPP horizontalcomponent deviation |
|
图 6 NYA2站双频SPP高程方向定位偏差 Fig. 6 NYA2 station dual-frequency SPP verticalcomponent positioning deviation |
|
|
表 3 双频SPP TGD改正前后定位精度 Tab. 3 Positioning accuracy before and after TGD correction of dual-frequency SPP |
由图 5和6可见,各双频组合SPP经TGD改正后水平及高程方向的定位精度均有大幅提升,且改正后精度相当,B1I/B2a在N方向的改正结果不如其他组合,但仅为个别现象。双频组合未改正前定位精度较差,会出现几十m的误差,经TGD改正后精度改善效果显著,且优于任意单频。
由表 3可见,各组合改正前后定位精度均相当,水平方向的定位精度由6~9 m提升至0.5~1.1 m,提升率为87%~91%;高程方向的定位精度由约11 m改正至2.5~4 m,提升率为66%~71%。由此可见,TGD改正对双频SPP效果显著,且双频提升率优于单频。经TGD改正后各双频组合在水平方向的定位精度基本优于1 m,高程方向优于4 m,较改正后的单频SPP精度更高。综上可知,硬件延迟偏差对SPP的定位精度影响较大,在定位解算中不可忽略。
3 结语1) BDS-3的DCB产品在1个月内的日解值稳定,未出现明显跳变,稳定性为0.08~0.30 ns,大部分卫星的月稳定性优于0.2 ns,TGD参数与DCB产品符合度高,大部分卫星之间的差异优于2 ns。BDS-3平均可见卫星数基本为8~11颗、PDOP平均约为2,说明BDS-3具有稳定的可见卫星数,且空间几何构型良好。
2) 单频SPP经TGD改正后水平和高程方向的定位精度均有大幅提升,且水平方向的改正率优于高程方向。水平方向的定位精度由2~4 m提升至1~2 m,改正率为30%~70%;高程方向的定位精度由约8 m提升至3~5 m,提升率为17%~50%,其中B1I和B1C频点的改正效果优于B2a。B3I频点未经TGD改正,但其与其余频点改正后的定位精度基本相当,E、N、U方向的RMSE分别为1.17 m、1.46 m和4.67 m。
3) 与单频SPP相同,各组合双频SPP经TGD改正后水平及高程方向的定位精度均有大幅提升,且改正后组合间的定位精度相当,水平方向的定位精度由6~9 m提升至1 m左右,提升率约为90%;高程方向的定位精度由11 m左右改正至2.5~4 m,提升率为66%~71%。经TGD改正后各组合双频SPP的定位精度优于任意单频SPP,水平方向基本优于1 m,高程方向优于4 m。TGD改正对单、双频SPP定位精度的影响较大,在定位解算中不可忽略。
| [1] |
王宁波, 袁运斌, 张宝成, 等. GPS民用广播星历中ISC参数精度分析及其对导航定位的影响[J]. 测绘学报, 2016, 45(8): 919-928 (Wang Ningbo, Yuan Yunbin, Zhang Baocheng, et al. Accuracy Evaluation of GPS Broadcast Inter-Signal Correction(ISC) Parameters and Their Impacts on GPS Standard Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 919-928)
(  0) 0) |
| [2] |
Dai P P, Ge Y L, Qin W J, et al. BDS-3 Time Group Delay and Its Effect on Standard Point Positioning[J]. Remote Sensing, 2019, 11(15): 1 819 DOI:10.3390/rs11151819
(  0) 0) |
| [3] |
Dai P P, Xing J P, Ge Y L, et al. The Effect of BDS-3 Time Group Delay and Differential Code Bias Corrections on Positioning[J]. Applied Sciences, 2020, 11(1): 104 DOI:10.3390/app11010104
(  0) 0) |
| [4] |
Guo F, Zhang X H, Wang J L. Timing Group Delay and Differential Code Bias Corrections for Beidou Positioning[J]. Journal of Geodesy, 2015, 89(5): 427-445 DOI:10.1007/s00190-015-0788-2
(  0) 0) |
| [5] |
Zhang Y Z, Wang H, Chen J P, et al. Calibration and Impact of Beidou Satellite-Dependent Timing Group Delay Bias[J]. Remote Sensing, 2020, 12(1): 192 DOI:10.3390/rs12010192
(  0) 0) |
| [6] |
李坤, 王潜心, 龚佑兴, 等. 基于TGD/DCB改正的BDS多频单点定位精度分析[J]. 合肥工业大学学报: 自然科学版, 2021, 44(5): 685-690 (Li Kun, Wang Qianxin, Gong Youxing, et al. Accuracy Analysis on BDS Multi-Frequency Point Positioning Based on TGD/DCB Corrections[J]. Journal of Hefei University of Technology: Natural Science, 2021, 44(5): 685-690 DOI:10.3969/j.issn.1003-5060.2021.05.019)
(  0) 0) |
| [7] |
谷世铭, 党亚民, 王虎, 等. 北斗差分码偏差改正对单点定位的影响[J]. 测绘科学, 2020, 45(10): 10-15 (Gu Shiming, Dang Yamin, Wang Hu, et al. The Effect of Beidou DCB Correction on Single Point Positioning[J]. Science of Surveying and Mapping, 2020, 45(10): 10-15)
(  0) 0) |
| [8] |
刘生锋, 杨文龙, 谷涛. BDS-3双频组合精密单点定位精度分析[J]. 测绘通报, 2021(3): 7-11 (Liu Shengfeng, Yang Wenlong, Gu Tao. Accuracy Analysis of BDS-3 Dual Frequency Combination Precision Point Positioning[J]. Bulletin of Surveying and Mapping, 2021(3): 7-11)
(  0) 0) |
| [9] |
曾添, 隋立芬, 鲍亚东, 等. BDS卫星端差分码偏差对定位的影响及改正模型研究[J]. 大地测量与地球动力学, 2017, 37(1): 53-57 (Zeng Tian, Sui Lifen, Bao Yadong, et al. The Impact of Satellite Differential Code Bias on BDS Positioning and Correction Model Research[J]. Journal of Geodesy and Geodynamics, 2017, 37(1): 53-57)
(  0) 0) |
| [10] |
王利军, 焦文海, 贾小林, 等. BDS-3精密单点定位性能比较分析[J]. 大地测量与地球动力学, 2021, 41(4): 357-361 (Wang Lijun, Jiao Wenhai, Jia Xiaolin, et al. Comparative Analysis of BDS-3 Precise Point Positioning Performance[J]. Journal of Geodesy and Geodynamics, 2021, 41(4): 357-361)
(  0) 0) |
| [11] |
袁海军, 章浙涛, 何秀凤, 等. 北斗三号卫星差分码偏差稳定性分析及其对单点定位的影响[J]. 武汉大学学报: 信息科学版, 2023, 48(3): 425-432 (Yuan Haijun, Zhang Zhetao, He Xiufeng, et al. Stability Analysis of BDS-3 Satellite Differential Code Bias and Its Impacts on Single Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2023, 48(3): 425-432)
(  0) 0) |
2. Xi'an Institute of Surveying and Mapping, 1 Mid-Yanta Road, Xi'an 710054, China;
3. School of Geological Engineering and Geomatics, Chang'an University, 126 Yanta Road, Xi'an 710054, China
 2023, Vol. 43
2023, Vol. 43


