2. 武汉地震科学仪器研究院有限公司,湖北省咸宁市青龙路11号,437000;
3. 湖北省重大工程地震检测与预警处置技术研究中心,湖北省咸宁市青龙路11号,437000
地震科学是观测科学,没有合格的观测资料,其内在规律是难以揭示的,而地下流体的动态观测与研究是地震科学的重要研究方向。地温是地热的主要表现方式之一,地热学作为地球物理学的一个分支,已有重要的发展。它是一个独立的物理量,与其他前兆方法相比,具有物理意义明确、物理量直观、资料易于分析、异常易于识别等特点[1]。许多地热问题与地壳中的构造和岩浆作用过程有关,这也是利用地热异常预报地震的原因之一[2]。水温变化是其中一项重要指标,微小的水温变化有可能反映地震孕育过程或其他地壳构造活动引起的热状态的变化,能间接地反映地震孕育过程,使其成为一种预报地震的重要监测项目。而地下水观测系统在观测过程中不可避免地存在噪声,同时环境中存在的工业噪声、天气噪声等也会对采集到的水温数据产生干扰,因此为了提高观测数据的可靠性与真实性,采用特殊的方法对数据中的噪声进行压制与处理是非常必要的。
传统的地下水温数据降噪处理方法中,小波变换能够在保证信息奇异性的同时很好地去除信号中的噪声干扰,但由于小波变换的基函数不存在自适应性,因此如果想要在去除噪声的同时保证信号本身的信息损失降到最低,就无法通过单一的小波变换实现。而经验模态分解(EMD)是一种处理非周期非平稳信号的常用方法,该方法依据信号自身的时间尺度特征对信号进行分解,具有自适应性,可以通过将部分高频的固有模态函数剔除从而提高信号的信噪比,但是EMD在分解过程中存在模态混叠现象,这会导致不同时间尺度成分出现在同一特征模态函数中。为解决这一问题,在EMD的基础上出现了一种通过加入白噪声辅助的数据分析方法——集合经验模态分解(EEMD),但同时该方法在信号分解过程中白噪声无法被完全消除,会影响后续的分析与处理。为此,有学者提出一种改进的自适应噪声完备集合经验模态分解方法(CEEMDAN)。CEEMDAN分解从两方面解决上述问题,一方面加入经EMD分解后含辅助噪声的模态分量,而不是将高斯白噪声信号直接添加在原始信号中;另一方面在得到第一阶模态分量后就进行总体平均计算,得到最终的一阶模态分量,然后对残余部分重复进行如上操作,这样便有效地解决了白噪声从高频到低频的转移传递问题。因此利用自适应噪声完备集合经验模态分解方法来弥补小波去噪所带来的信息丢失问题就成为一个很好的选择。
本文利用CEEMDAN对地下水温信号进行分解,通过计算相关系数对相关分量与无关分量进行区分,结合小波分析对仿真信号进行处理并与单一的小波阈值降噪、CEEMDAN降噪方法进行对比,比较信噪比(SNR)与均方误差(MSE),判断其降噪性能,同时利用该方法实现对实际采集到的包含噪声及异常的地下水温数据的降噪,观察其滤波效果。
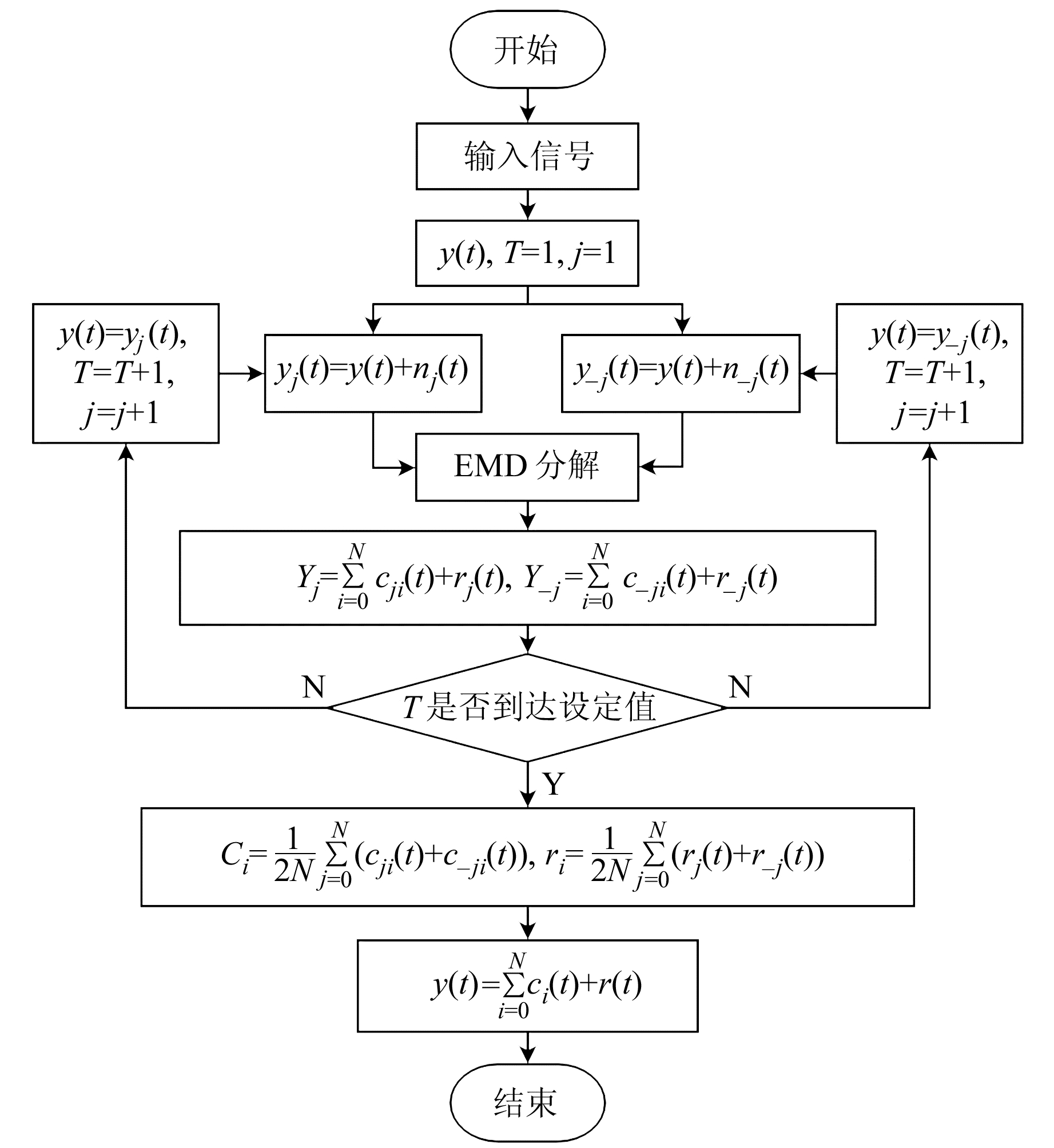
1 方法原理 1.1 CEEMDAN去噪及相关系数法CEEMDAN作为信号的分解方法,其原理流程如图 1所示,其中T为循环次数,nj(t)、n-j(t)为白噪声对。
|
图 1 CEEMDAN原理流程 Fig. 1 CEEMDAN principle flow |
具体分解过程如下:
1) 假设一个原始信号为y(n),在其基础上添加高斯白噪声eT(n),T=1, 2, …, N,其中N为添加白噪声的次数,从而得到含噪信号:
| $ y_T(n)=y(n)+e_T(n) $ | (1) |
2) 对新信号yT(n)进行EMD分解,得到其第1阶本征模态分量C1T。
3) 将得到的N个第一阶本征模态分量进行总体平均就可以得到CEEMDAN分解的第一个本征模态分量IMF1:
| $ \bar{C}_1=\frac{1}{N} \sum\limits_{T=1}^N C_1^T $ | (2) |
4) 计算去除第一个模态分量后的残差:
| $ r_1(n)=y(n)-\bar{C}_1 $ | (3) |
5) 在r1(n)中加入正负成对的高斯白噪声得到新的信号,对新得到的信号进行EMD分解,取其分解后的第一阶本征模态分量C2T, 从而可以计算出CEEMDAN分解后的第2个本征模态分量IMF2:
| $ \bar{C}_2=\frac{1}{N} \sum\limits_{T=1}^N C_2^T $ | (4) |
6) 计算去除第2个模态分量后的残差:
| $ r_2(n)=r_1(n)-\bar{C}_2 $ | (5) |
7) 重复上述步骤直到获得的残差信号为单调函数,不能继续分解为止。此时便得到原始信号y(n)的K个本征模态分量与残差rK(n),即
| $ y(n)=\sum\limits_{i=1}^K \bar{C}_i+r_K(n) $ | (6) |
这样就完成了对原始信号y(n)的CEEMDAN分解。
进一步利用CEEMDAN进行降噪则需要对原始信号进行分解后将信号的相关分量与不相关分量进行区分,之后利用相关分量进行信号的重构就可以得到滤波后的信号,重构信号的公式为:
| $ y^*(n)=\sum\limits_{i=k_{\mathrm{th}}}^N \operatorname{imf}^i(n)+\operatorname{res}(n) $ | (7) |
式中,imfi(n)为y(n)分解出的第i个IMF分量,N为分解IMF分量个数,res(n)为分解残差,kth为相关分量首次出现的位置。
对信号进行CEEMDAN分解后,kth的值可以通过计算y(n)与y*(n)的相关系数C(m)来确定[3-4]:
| $ C(m)=\frac{\sum\limits_{n=1}^L y(n) y_m^*(n)}{\sqrt{\sum\limits_{n=1}^L y^2(n) \sum\limits_{n=1}^L\left(y_m^*\right)^2(n)}} $ | (8) |
式中,L为信号y(n)的长度, 随m的增大C(m)应呈下降趋势,选择合适的阈值常数C0,取C(m)首次小于C0时m所对应的值, 则:
| $ k_{\mathrm{th}}=m+1 $ | (9) |
式中,C0的取值范围为[0.75, 0.85],之后的计算中取C0=0.8。综上所述,前kth-1项IMF分量为不相关分量,其余IMF分量为相关分量。
在对地下水温观测信号进行处理时,其噪声通常存在于高频部分,即不相关分量中,但同时由于不相关分量中还保存了一部分有效信号,如果直接利用CEEMDAN降噪方法对信号进行重构,会导致不相关分量部分的有效信息丢失,因此需通过小波变换对不相关分量进行进一步降噪处理,从而减小由于有效信息丢失而导致的信号失真[5]。
1.2 小波变换滤波器的设计作为一种被广泛应用于多个领域的信号分析方法,小波变换在信号的消噪处理方面有着优秀的性能。基于小波分析的降噪滤波器设计具体步骤如下[6]:
1) 选择合适的小波基函数和分解尺度,对含噪声的一维信号进行分解处理,可得:
| $ y(n)=x_1(n)+\varepsilon e_1(n), n=0, 1, 2, \cdots $ | (10) |
式中,y(n)为含噪信号,x1(n)为有用信号,e1(n)为噪声信号, ε为噪声系数的标准偏差。其中x1(n)保留了原信号的低频信息或近似信息,e1(n)保留了原信号的高频信息或细节信息。对x1(n)继续进行分解可得x2(n)与e2(n), 对x2(n)分解得x3(n)与e3(n)。依此类推,可多次进行分解,其分解过程如图 2。

|
图 2 小波变换分解流程树 Fig. 2 Wavelet transform decomposition process tree |
2) 为每一层的高频分量计算合适的阈值并选择阈值函数。
传统的小波阈值去噪算法中对阈值函数的选择通常比较单一,常为硬阈值函数或软阈值函数,其表达式分别如式(11)与式(12)所示:
| $ w_{j, k}^{\prime}=\left\{\begin{array}{l} w_{j, k}, \left|w_{j, k}\right| \geqslant \lambda \\ 0, \left|w_{j, k}\right|<\lambda \end{array}\right. $ | (11) |
| $ w_{j, k}^{\prime}=\left\{\begin{array}{l} \operatorname{sgn}\left(w_{j, k}\right)\left(\left|w_{j, k}\right|-\lambda\right), \left|w_{j, k}\right| \geqslant \lambda \\ 0, \left|w_{j, k}\right|<\lambda \end{array}\right. $ | (12) |
式中,λ为门限阈值,wj, k为测试信号小波系数,w′j, k为估计后的小波系数,j为分解尺度。
由于硬阈值函数在分界点处的左右极限不相同,信号导数不连续,导致信号在设定的临界点处存在突变,产生Gibbs效应,从而使去噪后信号在局部有较大的振荡。而软阈值函数由于在分解点处是连续的,因而比硬阈值去噪后的波形更加平滑,但同时由于在|wj, k|≥λ的范围内总是存在恒定偏差,使得进行小波重构后的信号失真,与原信号之间存在无法消除的误差。
为了对传统阈值函数进行优化,本文采用了一种改进阈值函数,其表达式如下:
| $ w_{j, k}^{\prime}=\left\{\begin{array}{l} w_{j, k}-\frac{\lambda}{2 \mathrm{e}^{\frac{\left(w_{j, k}-\lambda\right)^2}{\tau}}}-\frac{\lambda}{2 \mathrm{e}^{\frac{1}{\tau}}}, w_{j, k} \geqslant \lambda \\ 0, \left|w_{j, k}\right|<\lambda \\ w_{j, k}+\frac{\lambda}{2 \mathrm{e}^{\frac{\left(w_{j, k}-\lambda\right)^2}{\tau}}}+\frac{\lambda}{2 \mathrm{e}^{\frac{1}{\tau}}}, w_{j, k} \leqslant-\lambda \end{array}\right. $ | (13) |
在改进的阈值函数中,通过调整τ的取值,就可以实现在软阈值函数与硬阈值函数之间平滑切换,从而获得最佳降噪效果,其中τ越大则改进的阈值函数越接近软阈值函数。3种阈值函数的算法特性对比如图 3。
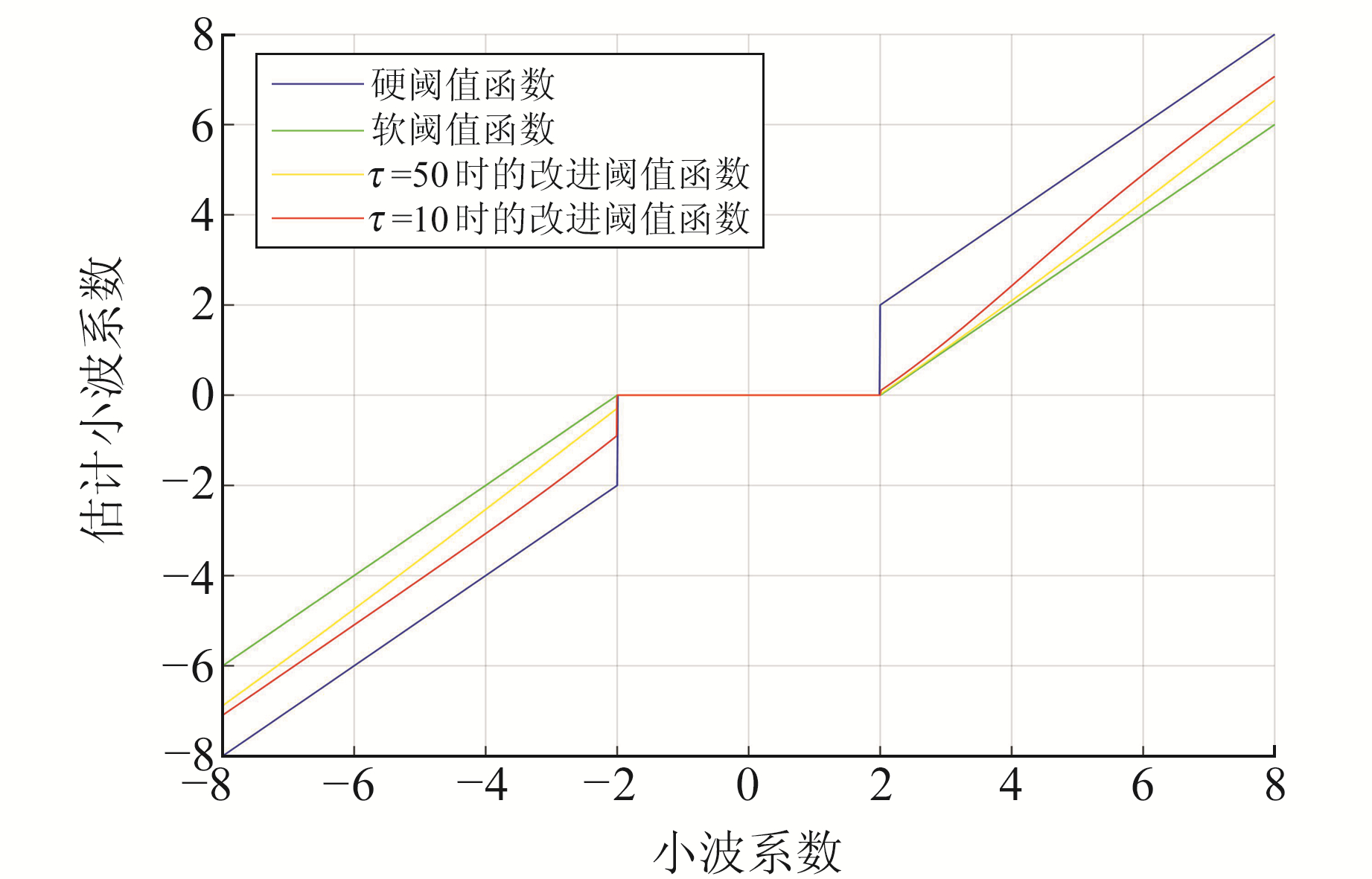
|
图 3 3种阈值函数的比较 Fig. 3 Comparison of three threshold functions |
可以看出,改进阈值函数具有更好的数学特性,通过选择合适的τ,既降低了硬阈值函数在阈值点处间断而导致的局部振荡,又减小了软阈值函数所存在的恒定误差,因此去噪效果更加平滑且去噪后更加接近真实信号。
3) 利用分解得到的低频系数和经过阈值降噪处理后的高频系数进行信号的小波重组。
1.3 结合CEEMDAN的小波阈值降噪方法在对以上两种算法的优缺点进行分析后,本文提出利用CEEMDAN结合小波阈值降噪算法对地下水温数据信号进行去噪,其算法流程如图 4所示。首先将原始信号进行自适应噪声完备集合经验模态分解,得到IMF分量与残差;之后通过计算IMF分量与原信号的相关系数将相关分量与不相关分量进行区分,对相关分量进行适当的平滑处理,不相关分量则进一步设计小波分析滤波器对其进行滤波处理;最后将经过小波分析滤波器处理后的不相关分量与经过平滑处理的相关分量结合,从而得到降噪后的信号。

|
图 4 降噪算法流程 Fig. 4 Noise reduction algorithm flow |
在对水温数据的观测过程中,既存在由观测技术系统干扰、观测环境变化及人为干扰等因素所引起的外部噪声,也存在由系统热噪声、信号传输噪声等组成的内部噪声[7],因此水温信号可视为一种非线性、非平稳信号,可表示为:
| $ y(t)=x(t)+e(t)+q(t) $ | (14) |
式中,x(t)为水温信号的真实值,e(t)为外部噪声,q(t)为内部噪声。外部噪声e(t)通常为宽频带、短脉冲的无规律信号,可以通过对数据视具体情况增加窄带滤波器进行剔除。系统内部噪声q(t)由于其幅值具有连续性、相位随机,因此可以视作白噪声,采用结合CEEMDAN的小波阈值降噪方法进行滤波处理。
2.2 模拟数据测试分析为了体现本文提出方法的优越性,结合地下流体温度信号的特点,利用MATLAB中的bumps函数产生一个测试信号,并添加随机白噪声,分别利用传统小波阈值降噪、改进小波阈值降噪、CEEMDAN降噪方法及结合CEEMDAN与相关系数分析的改进小波阈值降噪方法对产生的含噪信号进行滤波,通过计算信噪比(SNR)与均方误差(MSE)来进行对比分析,其降噪效果对比见图 5。
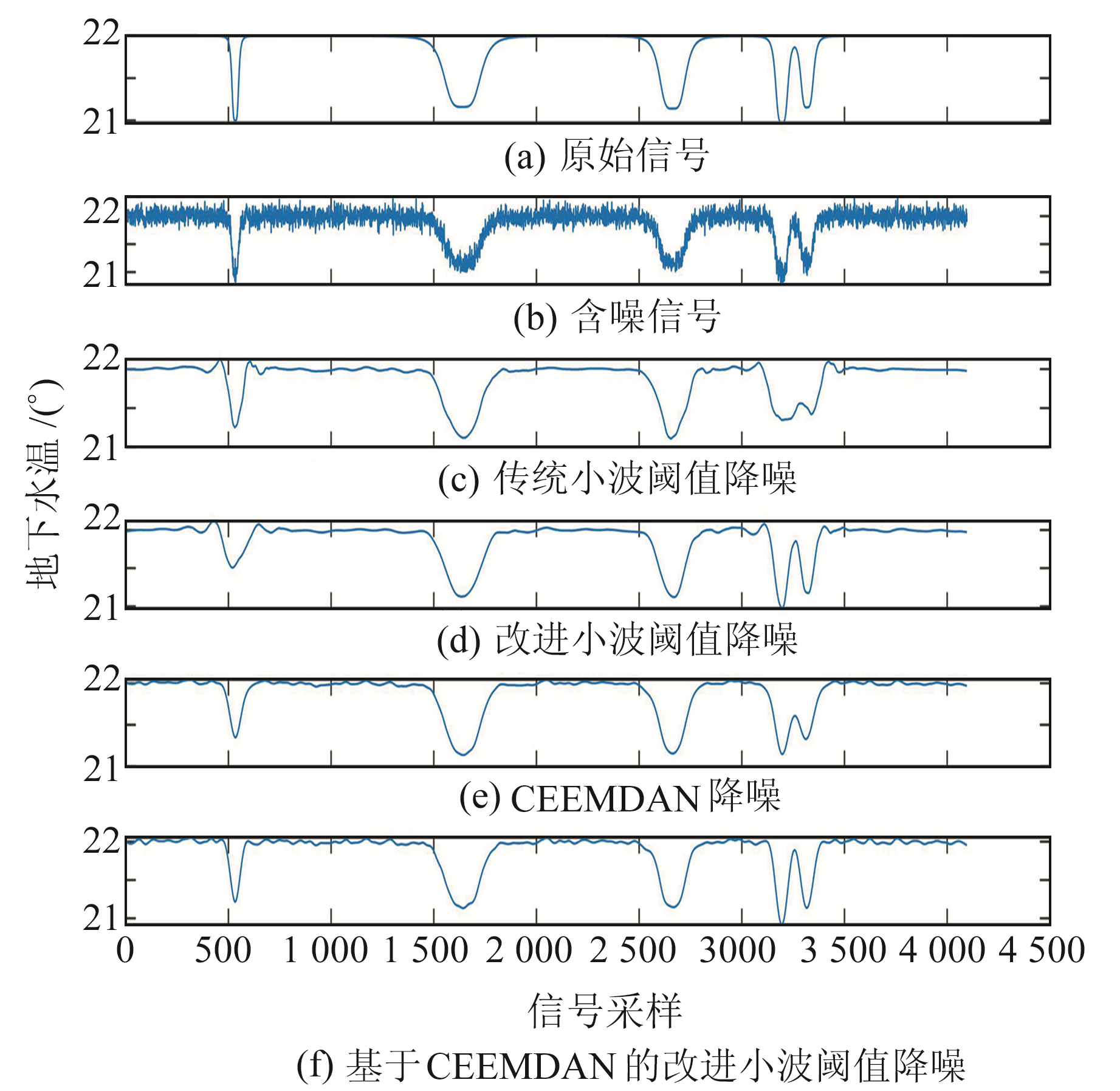
|
图 5 不同方法下的降噪效果对比 Fig. 5 Comparison of noise reduction effects of different methods |
从图 5可以看出,传统的小波阈值降噪能够有效地去除噪声信号,但由于所采用的硬阈值函数会导致信号在分界点处的导数不连续,从而产生Gibbs现象。相比之下改进后的阈值函数则很好地减轻了减噪信号在分界处的越变。
由CEEMDAN进行分解降噪后的信号比起其他降噪方法得到的波形更加平滑,但同时信号在某些特征点处的突变也由于高频分量的直接去除而丢失,这也导致了信号完整性的破坏与细节的缺失。而结合CEEMDAN的改进小波阈值降噪在去除噪声的同时既改善了小波阈值降噪的阈值函数引起的Gibbs现象,也更好地保留了原信号的细节部分。上述各降噪算法的性能对比见表 1。
|
|
表 1 不同降噪算法性能对比 Tab. 1 Performance comparison of different noise reduction algorithms |
通过对比图 5与表 1可以看出,相较于单一的小波阈值降噪或是CEEMDAN降噪,本文提出的结合CEMMDAN的改进小波阈值降噪算法信噪比更高,同时均方误差也更小,具有最优秀的降噪性能。
3 实际地下水温数据处理为进一步验证结合CEEMDAN的改进小波阈值降噪算法的有效性,通过对地下水温的实际数据进行降噪处理,以证明其在实际地下流体监测过程中能起到更好的噪声压制作用。图 6为汉南地震台2022-03~04采集到的地下水温度数据,接收的信号受环境干扰包含大量的噪声,会影响到分析研究数据的准确性。而采集到的水温信号具有非线性、非平稳、非周期等特点,基于CEEMDAN的改进小波阈值降噪算法能够很好地适用于此类数据处理。
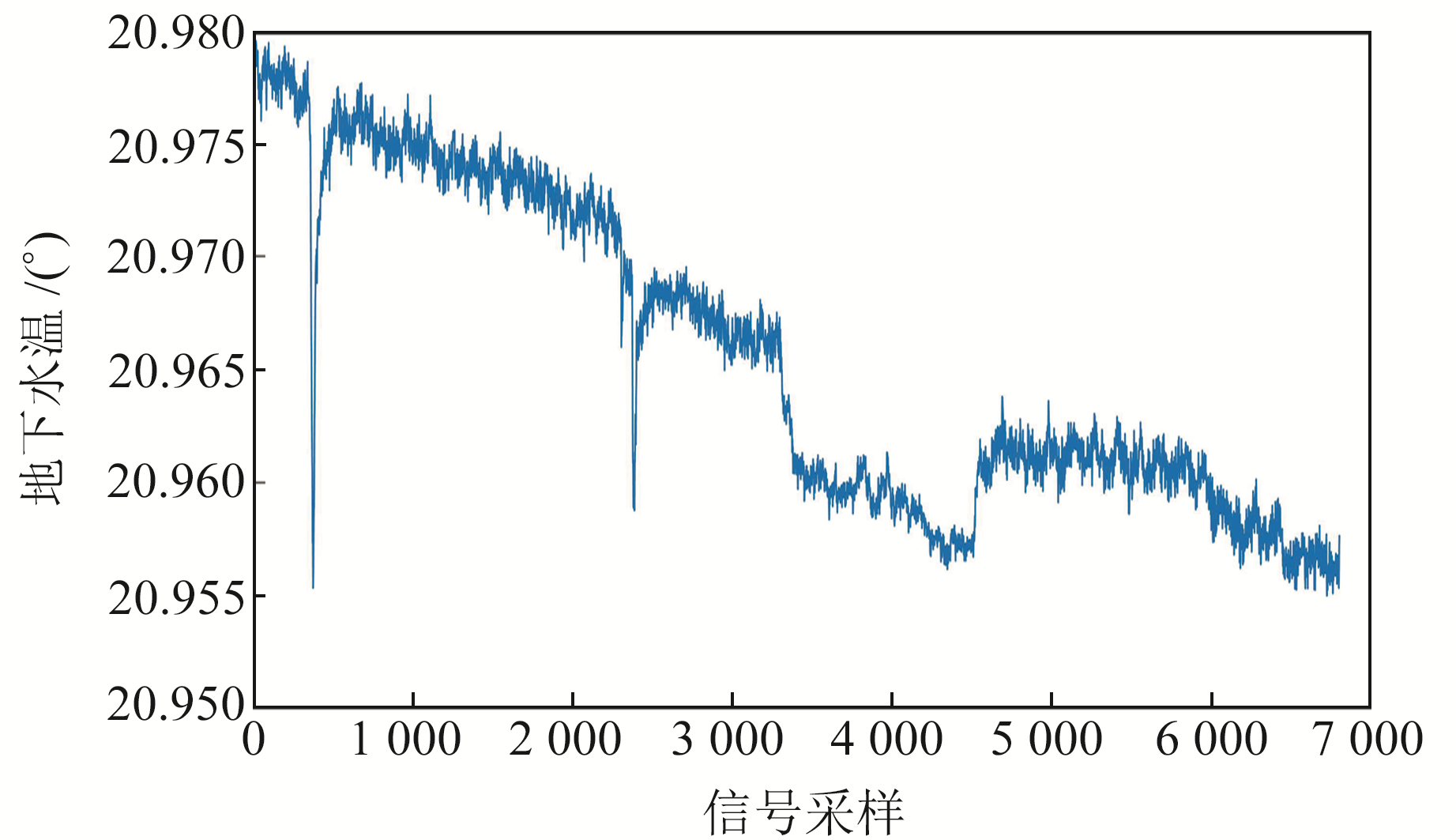
|
图 6 地下水温度信号 Fig. 6 Groundwater temperature signal |
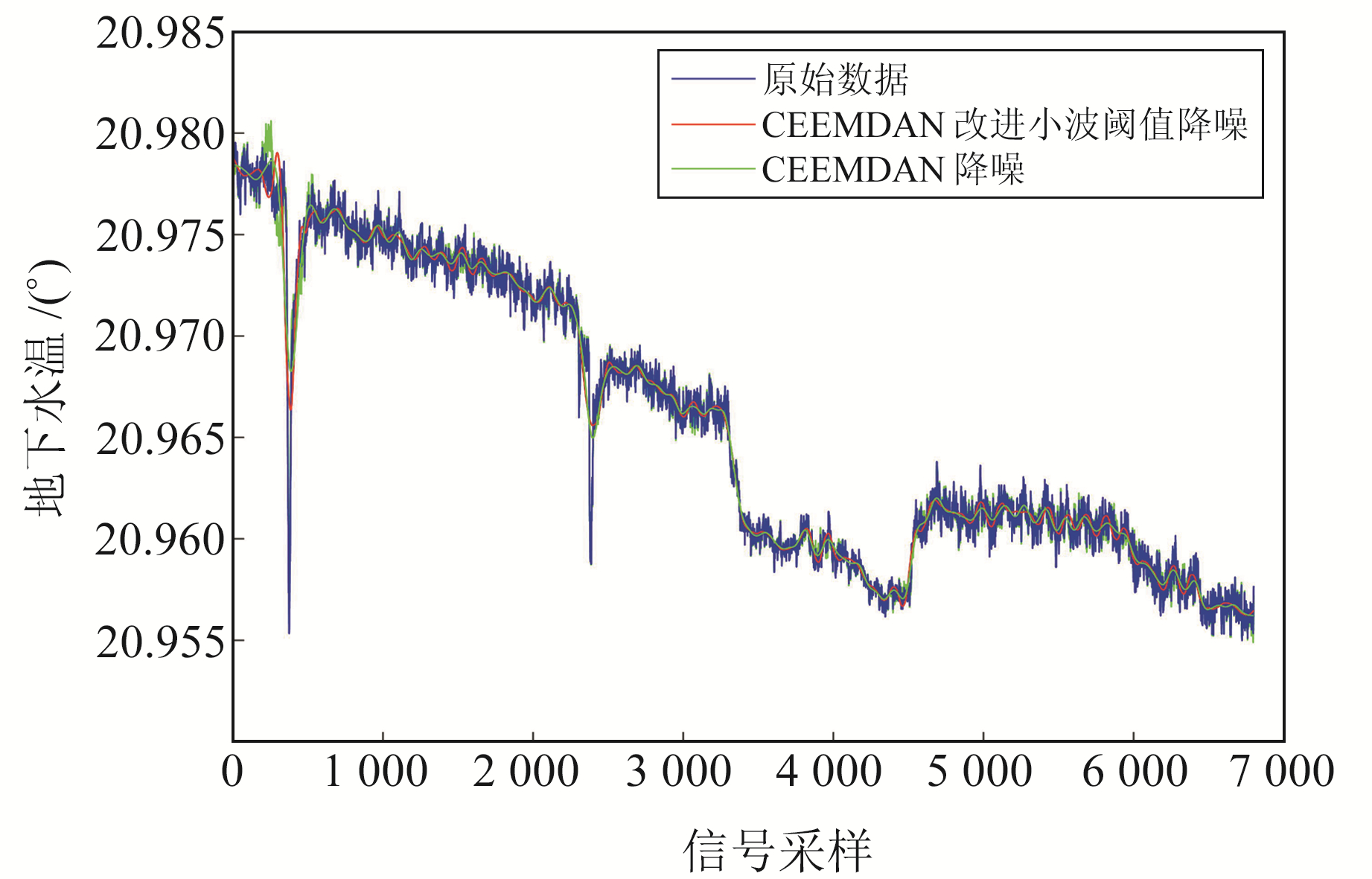
首先对水温数据进行CEEMDAD分解,由图 7可以看出,信号被分解为9层,分别计算每层IMF分量与原信号的相关系数,从而确定前3层(上面3层)为不相关分量,只需针对前3层进行小波阈值降噪。利用改进小波阈值降噪方法取固定阈值对前3层IMF分量进行降噪处理,将处理后的分量与其他分量及残差RES合成即得到滤波后的降噪信号,其降噪效果如图 8中红线所示。

|
图 7 地下水温信号的CEEMDAN分解 Fig. 7 CEEMDAN of groundwater temperature signal |
|
图 8 降噪效果对比 Fig. 8 Comparison of noise reduction effect |
从图 7和图 8可以看出,相比于单一CEEMDAN降噪(图 8中绿线),结合CEEMDAN的改进小波阈值降噪算法进行去噪后所得到的曲线在连续部分更加贴合温度本身变化趋势的同时,也减小了突变部分的失真情况,更好地呈现了数据的异常部分,使有用信息得到很好的保留,表现出较单一滤波手段更好的效果。
4 结语经过对仿真信号模型根据信噪比与均方误差的分析及对实际水温数据处理结果的分析表明,相较于单一的小波阈值降噪或者CEEMDAN降噪,本文提出的结合CEEMDAN的改进小波阈值降噪方法对地下流体观测信号的噪声压制能力更佳,滤波后的信号曲线更平滑,在实际应用中表现出更加优秀的性能。
| [1] |
穆志军, 邓月飞. 云南曲江井水温观测干扰及震前异常分析[J]. 高原地震, 2017, 29(3): 11-15 (Mu Zhijun, Deng Yuefei. Analysis on Water Temperature Observation Disturbance and Anomaly of Qujiang Well before Earthquake in Yunnan[J]. Plateau Earthquake Research, 2017, 29(3): 11-15)
(  0) 0) |
| [2] |
胡爱真, 高慧慧, 张晓清. 昆仑山口西8.1级地震前气象地温异常特征分析[J]. 高原地震, 2002, 14(1): 76-82 (Hu Aizhen, Gao Huihui, Zhang Xiaoqing. Analysis on the Anomaly Characteristics of Meteorological Geotemperature before the West Kunlun Mountains Earthquake with MS8.1[J]. Platean Earthquake Research, 2002, 14(1): 76-82)
(  0) 0) |
| [3] |
Duan Y B, Song C T. Relevant Modes Selection Method Based on Spearman Correlation Coefficient for Laser Signal Denoising Using Empirical Mode Decomposition[J]. Optical Review, 2016, 23(6): 936-949 DOI:10.1007/s10043-016-0275-x
(  0) 0) |
| [4] |
Zhang S Y, Liu Y Y, Yang G L. EMD Interval Thresholding Denoising Based on Correlation Coefficient to Select Relevant Modes[C]. The 34th Chinese Control Conference(CCC), Hangzhou, China, 2015
(  0) 0) |
| [5] |
Zheng Y, Li S, Xing K, et al. A Novel Noise Reduction Method of UAV Magnetic Survey Data Based on CEEMDAN, Permutation Entropy, Correlation Coefficient and Wavelet Threshold Denoising[J]. Entropy(Basel, Switzerland), 2021, 23(10): 1 309
(  0) 0) |
| [6] |
Yu Y, Shang Q, Xie T. A Hybrid Model for Short-Term Traffic Flow Prediction Based on Variational Mode Decomposition, Wavelet Threshold Denoising, and Long Short-Term Memory Neural Network[J]. Complexity, 2021, 2021: 1-24
(  0) 0) |
| [7] |
文勇, 吴哲, 孟鑫, 等. 德令哈地震台水温观测数据干扰[J]. 地震地磁观测与研究, 2018, 39(5): 143-149 (Wen Yong, Wu Zhe, Meng Xin, et al. Interference Analysis of Surface Water Temperature Data at Delingha Seismic Station[J]. Seismological and Geomagnetic Observation and Research, 2018, 39(5): 143-149)
(  0) 0) |
2. Wuhan Institute of Seismic Scientific Instrument Co Ltd, 11 Qinglong Road, Xianning 437000, China;
3. Engineering Technology Research Center for Earthquake Monitoring and Early Warning Disposal of Major Projects in Hubei Province, 11 Qinglong Road, Xianning 437000, China
 2023, Vol. 43
2023, Vol. 43


